샘플 데이터와 Decision Tree Classification
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
data = {
"value": [30, 120, 150, 390, 400, 300, 500],
"label": [0, 0, 1, 0, 0, 1, 0]
}
data = pd.DataFrame(data)
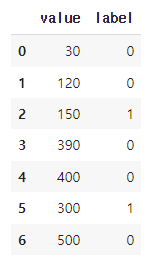
print(data)위 코드는 pandas, numpy, matplotlib.pyplot 모듈을 불러온 후, 7개의 데이터를 가지고 있는 DataFrame을 만들고 출력하는 코드입니다.
데이터는 "value"와 "label" 두 개의 열(column)을 가지고 있으며, "value"는 정수형으로 7개의 숫자값이 있고, "label"은 이진(binary) 데이터로 0과 1로 이루어져 있습니다.
Decision Tree 구현
- 변수 값에 따라 데이터를 정렬
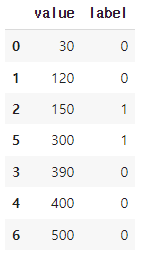
sorted_data = data.sort_values(by="value")
sorted_data = sorted_data.reset_index(drop=True)해당 코드는 "value" 변수에 따라 데이터를 정렬하고, "label" 변수에 따른 레이블 값이 바뀌는 지점에서 경계값을 찾아내는 코드입니다.
먼저, "value" 변수에 따라 데이터를 정렬하기 위해 sort_values() 함수를 사용합니다. 그 후, 데이터 프레임의 인덱스를 0부터 순차적으로 재설정하기 위해 reset_index() 함수를 사용합니다.
- 정답이 바뀌는 경계 지점을 찾는다.
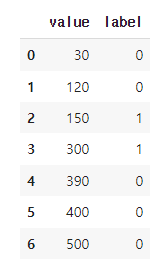
boundary = sorted_data["label"].diff() != 0
boundary[0] = False
boundary_idx = boundary.loc[boundary].index다음으로, diff() 함수를 사용하여 이전 값과 비교하여 "label" 변수의 값이 바뀌는 부분을 찾아냅니다. 그 후, 첫 번째 경계값을 False로 변경합니다. 이후, loc() 함수를 사용하여 경계값이 존재하는 인덱스를 추출합니다. 추출된 인덱스는 "boundary_idx" 변수에 저장됩니다.
즉, sorted_data["label"].diff(): label 변수를 바로 이전 값과 차분한 결과를 출력합니다. 즉, 이전 데이터와 현재 데이터의 label 값의 차이를 구합니다.
!= 0: 이전 데이터와 현재 데이터의 label 값의 차이가 0이 아닌 경우 True를, 0인 경우 False를 출력합니다.
boundary[0] = False: 첫 번째 데이터는 이전 데이터와의 차이가 없기 때문에 False로 설정합니다.
boundary.loc[boundary].index: boundary 변수에서 True인 index 값을 추출합니다. 이 값은 정답이 바뀌는 지점의 index를 의미합니다.
따라서, 해당 코드는 정답이 바뀌는 지점을 찾는 것이고, 이후 경계 지점을 찾는 과정에서 사용됩니다.


- 경계의 평균값을 기준으로 잡는다.
idx_1 = boundary_idx[0] #첫 번째 경계 구간
data.loc[[idx_1-1, idx_1]]
bound_value_1 = data.loc[[idx_1-1, idx_1], "value"].mean()
idx_2 = boundary_idx[1] #두 번째 경계 구간
bound_value_2 = data.loc[[idx_2-1, idx_2], "value"].mean()위 코드는 연속형 변수의 경계값을 찾는 과정 중에, 구간별 경계값을 찾기 위해 사용됩니다.
먼저, boundary라는 변수를 만들어 정답이 바뀌는 경계 지점을 찾습니다. 이를 위해서는 정답(label)의 차분값을 계산하여 0이 아닌 값이 있는 위치를 찾으면 됩니다. 따라서 sorted_data["label"].diff() != 0으로 차분값이 0이 아닌 지점을 boolean 형태로 구합니다. 이 때, 첫 번째 구간의 이전 구간도 같은 구간에 포함되므로 boundary[0] = False로 수정해줍니다.
그 다음, boundary.loc[boundary].index를 이용하여 boolean 형태의 boundary에서 True인 위치(index)를 추출합니다. 이 때, 반환되는 인덱스는 sorted_data에서의 위치를 의미하므로, 이를 활용해 data에서 구간별 경계값을 추출합니다.
첫 번째 경계 구간에서는 첫 번째와 두 번째 데이터의 평균을 구하면 되므로, data.loc[[idx_1-1, idx_1], "value"].mean()으로 평균값을 계산합니다. 두 번째 경계 구간에서는 두 번째와 세 번째 데이터의 평균을 구하면 되므로, data.loc[[idx_2-1, idx_2], "value"].mean()으로 평균값을 계산합니다.
- 구간별 경계값을 기준으로 정보 이득을 계산한다.
def gini_index(label):
p1 = (label == 0).mean()
p2 = 1 - p1
return 1 - (p1 ** 2 + p2 **2)
def concat_gini_index(left, right):
left_gini = gini_index(left)
right_gini = gini_index(right)
all_num = len(left) + len(right)
left_gini *= len(left) / all_num
right_gini *= len(right) / all_num
return left_gini + right_ginigini_index(label) : 인자로 받은 라벨 데이터를 이용해 지니 지수를 계산하는 함수입니다. p1은 라벨이 0인 비율을 계산한 뒤, p2는 라벨이 1인 비율을 계산하여 지니 지수 공식에 대입하고 반환합니다.
concat_gini_index(left, right) : 인자로 받은 왼쪽 노드와 오른쪽 노드 데이터의 지니 지수를 합산한 값을 반환하는 함수입니다. 먼저 gini_index() 함수를 사용해 왼쪽 노드와 오른쪽 노드의 지니 지수를 계산한 뒤, 두 지니 지수를 각각 노드 데이터 개수의 비율로 가중 평균한 값을 합산하여 반환합니다.
135를 경계로 나눌 때
left_1 = sorted_data.loc[:idx_1 - 1, "label"]
right_1 = sorted_data.loc[idx_1:, "label"]이 코드는 idx_1을 경계로 데이터를 좌우로 나누는 코드입니다. idx_1은 boundary_idx 리스트에서 첫 번째 경계 구간의 인덱스를 의미합니다.
따라서 left_1은 idx_1을 기준으로 왼쪽에 있는 데이터의 label 컬럼을, right_1은 오른쪽에 있는 데이터의 label 컬럼을 저장하게 됩니다.

345를 경계로 나눌 때
left_2 = sorted_data.loc[:idx_2 - 1, "label"]
right_2 = sorted_data.loc[idx_2:, "label"]
이 코드는 idx_2을 경계로 데이터를 좌우로 나누는 코드입니다. idx_2는 boundary_idx 리스트에서 두 번째 경계 구간의 인덱스를 의미합니다.
따라서 left_2은 idx_2을 기준으로 왼쪽에 있는 데이터의 label 컬럼을, right_2은 오른쪽에 있는 데이터의 label 컬럼을 저장하게 됩니다.

Decision Tree Package
from sklearn.tree import DecisionTreeClassifier, plot_tree
tree = DecisionTreeClassifier(max_depth=1)
tree.fit(data["value"].to_frame(), data["label"])
plot_tree(tree)코드에서는 DecisionTreeClassifier를 사용하여 의사결정나무 모델을 만들고, max_depth=1을 설정하여 최대 깊이를 1로 제한합니다. fit() 메서드를 사용하여 모델을 학습시키고, plot_tree() 함수를 사용하여 모델을 시각화합니다. 최대 깊이가 1이므로, 나무의 깊이는 루트 노드(0번 노드)와 하나의 끝 노드(1번 노드)로 구성됩니다.

