샘플 데이터와 Decision Tree Regressor
Decision Tree Regressor는 지도학습 알고리즘 중 하나로, 입력값과 해당 출력값의 연속적인 데이터를 이용해 예측 모델을 생성하는데 사용됩니다.
예를 들어, 아파트의 가격을 예측한다고 가정해봅시다. 이 때, 우리는 아파트의 크기, 위치, 층수 등의 정보를 가지고 해당 아파트의 가격을 예측할 수 있습니다. 이러한 데이터를 이용하여 Decision Tree Regressor를 학습시키면, 새로운 아파트의 크기, 위치, 층수 등의 정보를 입력하면 해당 아파트의 가격을 예측할 수 있습니다.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
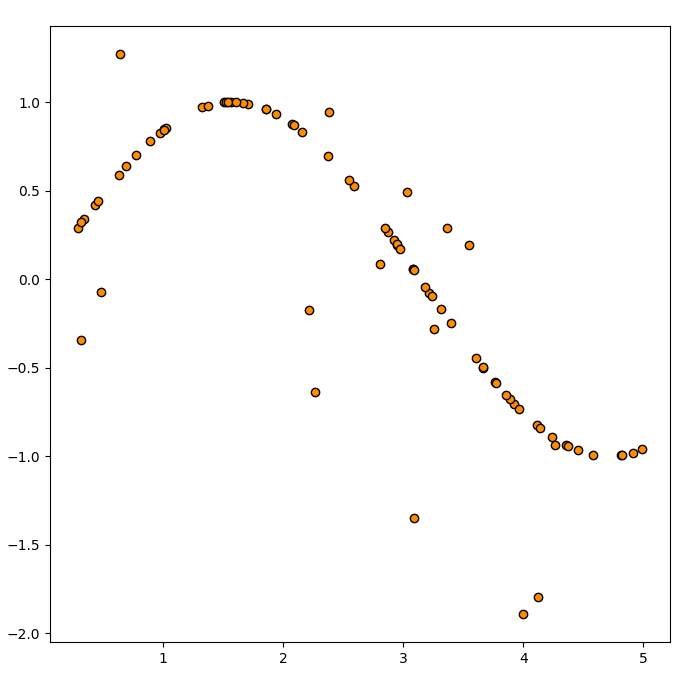
data = np.sort(np.random.uniform(low=0, high=5, size=(80, 1))) #예시에서 사용할 샘플 데이터를 생성
label = np.sin(data).ravel()
label[::5] += 3 * (0.5 - np.random.uniform(0, 1, 16))
#데이터는 하나의 변수를 가지며 변수에 따른 정답은 아래처럼 생겼습니다.
plt.figure(figsize=(8, 8))
plt.scatter(data, label, edgecolor="black", c="darkorange")이 코드는 NumPy와 Matplotlib 라이브러리를 이용하여 샘플 데이터를 생성하고, 해당 데이터를 시각화하는 코드입니다.
np.random.seed(2021) : 난수 생성 시드를 2021로 설정하여, 실행할 때마다 같은 난수를 생성할 수 있도록 합니다.
data = np.sort(np.random.uniform(low=0, high=5, size=(80, 1))) : 0부터 5까지의 범위에서 80개의 난수를 생성하여, 이를 오름차순으로 정렬하여 80 x 1 크기의 2차원 배열로 만듭니다.
label = np.sin(data).ravel() : np.sin() 함수를 이용하여 data에 해당하는 각도의 사인 값을 계산하고, 이를 1차원 배열로 만듭니다.
label[::5] += 3 * (0.5 - np.random.uniform(0, 1, 16)) : label 배열에서 5개씩 뛰어넘으면서, 해당 인덱스에 해당하는 값에 랜덤한 값을 더해줍니다. 이 때, 랜덤한 값은 0부터 1까지의 균일 분포에서 생성되는 값의 16개입니다.
plt.figure(figsize=(8, 8)) : 새로운 그림을 그리고, 크기를 8x8로 설정합니다.
plt.scatter(data, label, edgecolor="black", c="darkorange") : 산점도를 그리는 함수입니다. x축에는 data, y축에는 label을 사용하며, 경계선 색상은 검정색, 산점도 색상은 어두운 주황색으로 설정합니다.
결과적으로, 이 코드를 실행하면 변수(data)에 대한 정답(label)을 시각화하여 볼 수 있습니다.
Viz Data 시각화를 위한 데이터도 생성해보자!
# Viz Data 시각화를 위한 데이터를 생성하는 코드
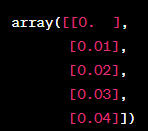
viz_test_data = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
print(viz_test_data[:5])이 코드는 Viz Data 시각화를 위한 데이터를 생성하는 코드입니다.
np.arange(0.0, 5.0, 0.01) : 0부터 5까지 0.01의 간격으로 값을 생성합니다.
[:, np.newaxis] : 생성된 값들을 2차원 배열로 만듭니다.
즉, viz_test_data는 0부터 4.99까지 0.01의 간격으로 생성된 값을 열로 가지는 2차원 배열입니다.
Decion Tree Regressor : Tree의 분할이 이루어질 때마다 어떻게 예측을 하는지 알아보자!
Decision Tree Regressor는 트리(Tree) 구조를 이용한 회귀(Regression) 분석 모델입니다. 모델이 예측을 할 때, 트리의 분할(Split)이 이루어질 때마다 해당 분할에 속하는 데이터의 예측값을 계산합니다. 이 계산 방법은 다음과 같습니다.
각 분할에서 속하는 데이터의 예측값을 해당 분할에 속하는 데이터의 실제값의 평균으로 계산합니다.
예측값이 계산된 분할에서 해당 분할에 속하는 모든 데이터의 예측값을 해당 분할의 예측값으로 합니다.
즉, 예측값을 계산하는 과정에서 트리의 분할이 반영되며, 이를 통해 전체 데이터셋에 대한 예측값을 계산합니다.
plot_tree() 함수는 학습된 Decision Tree 모델을 시각화합니다. 트리 구조에서 각 노드(Node)는 특정 변수와 해당 변수의 분할 기준값을 가지며, 각 분할에 따른 예측값과 샘플 수를 보여줍니다. 이를 통해 모델이 어떤 변수와 기준값에 따라 데이터를 분할하며 예측하는지 시각적으로 확인할 수 있습니다.
from sklearn.tree import DecisionTreeRegressor, plot_tree- 분할이 없을 경우
분할이 없는 경우에는 학습 데이터의 평균으로 예측을 합니다.
viz_test_pred = np.repeat(label.mean(), len(viz_test_data))
#Plot으로 보면 강의에서 본 하나의 선이 생깁니다.
plt.figure(figsize=(8, 8))
plt.scatter(data, label, edgecolor="black", c="darkorange")
plt.plot(viz_test_data, viz_test_pred, color="C2")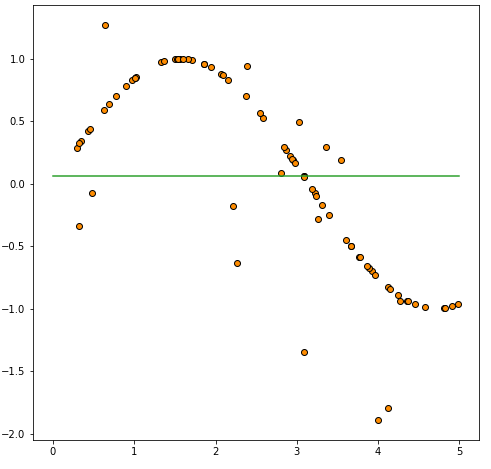
분할이 없을때의 mse variance를 계산하면 다음과 같습니다.
train_pred = np.repeat(label.mean(), len(data))
mse_var = np.var(label - train_pred)
print(f"no divide mse variance: {mse_var:.3f}")
위 코드는 분할이 없는 경우에 대한 예측과 MSE Variance를 계산하는 코드입니다.
먼저, np.repeat(label.mean(), len(viz_test_data))은 학습 데이터의 평균을 viz_test_data의 길이만큼 반복하여 생성한 것입니다. 이를 viz_test_pred에 저장합니다. 이렇게 하면 viz_test_data에 대한 예측값이 모두 학습 데이터의 평균이 됩니다.
그리고 이를 시각화하기 위해 plt.plot(viz_test_data, viz_test_pred, color="C2")을 사용합니다. 이렇게 하면 viz_test_data에 대한 예측값을 나타내는 하나의 수평선이 그려집니다.
(즉, 초록색 선이 예측값을 나타냄!)
마지막으로, 학습 데이터에 대한 예측값을 train_pred에 저장하고, 실제값 label에서 이를 빼서 MSE Variance를 계산합니다. 분할이 없는 경우에는 모든 데이터가 예측값이 동일하므로 MSE Variance는 0이 됩니다.
1. 첫 번째 분할
first_divide = DecisionTreeRegressor(max_depth=1)
first_divide.fit(data, label)
first_divide_pred = first_divide.predict(viz_test_data)
#첫번째로 분할되서 나누어진 영역을 그리면 아래와 같습니다.
plt.figure(figsize=(8, 8))
plt.scatter(data, label, edgecolor="black", c="darkorange")
plt.axvline(first_divide.tree_.threshold[0], color="red")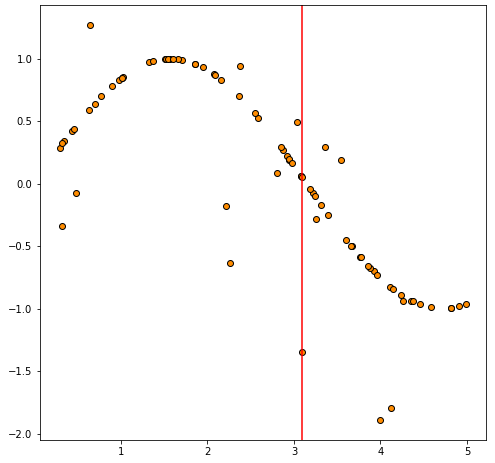
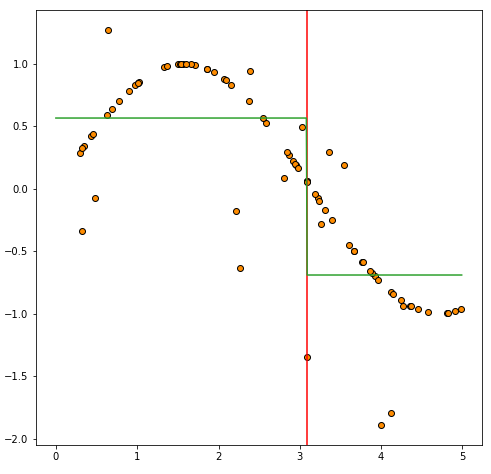
분할이 이루어진 각 영역에서 다시 평균을 계산합니다.
plt.figure(figsize=(8, 8))
plt.scatter(data, label, edgecolor="black", c="darkorange")
plt.axvline(firstdivide.tree.threshold[0], color="red")
plt.plot(viz_test_data, first_divide_pred, color="C2")
Treef를 시각화하기 위해서는 plot_tree 함수를 이용하면 됩니다.
Tree를 시각화하면 아래와 같습니다.
plot_tree(first_divide)
위 코드는 Decision Tree Regressor를 사용하여 첫 번째 분할을 수행하고, 그 결과를 시각화하는 코드입니다.
첫 번째 분할을 수행하기 위해 DecisionTreeRegressor(max_depth=1)을 사용합니다. 이는 분할을 1번만 수행하겠다는 의미입니다. 그리고 이 모델을 data와 label 데이터를 사용하여 학습시킵니다.
학습된 모델을 사용하여 viz_test_data에 대한 예측값을 계산하고, 이를 first_divide_pred에 저장합니다. 이렇게 하면 첫 번째 분할로 생성된 두 개의 영역에 대한 예측값이 계산됩니다.
그리고 이를 시각화하기 위해 먼저 첫 번째 분할이 일어난 지점을 나타내기 위해 plt.axvline(firstdivide.tree.threshold[0], color="red")을 사용합니다. 이렇게 하면 분할된 두 개의 영역을 나누는 수직선이 그려집니다.
그리고 이어서 분할된 두 개의 영역에 대한 예측값을 plt.plot(viz_test_data, first_divide_pred, color="C2")을 사용하여 시각화합니다. 이렇게 하면 두 개의 직선이 그려집니다.
마지막으로, 생성된 Decision Tree Regressor를 시각화하기 위해서는 plot_tree(first_divide)을 사용합니다. 이렇게 하면 생성된 Decision Tree를 시각화할 수 있습니다.
2. 두 번째 분할
second_divide = DecisionTreeRegressor(max_depth=2) #depth를 2로 주어서 분할 2번
second_divide.fit(data, label)
second_divide_pred = second_divide.predict(viz_test_data)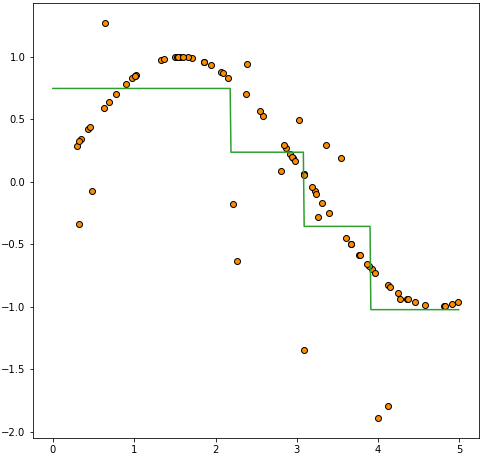
plot_tree(second_divide)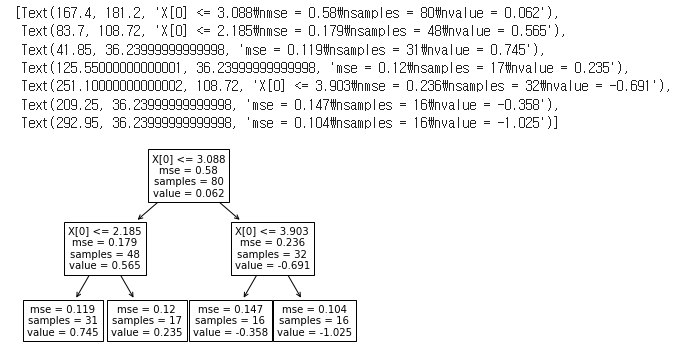
두 번째 분할에서는 첫 번째 분할과 마찬가지로 먼저 가장 중요한 변수를 선택한 후, 해당 변수를 기준으로 데이터를 둘로 나누게 됩니다.
이번에는 두 개의 영역이 생성되었으므로, 각각의 영역에서 평균을 구하게 됩니다. 이렇게 구한 두 개의 평균을 바탕으로, 해당 변수의 기준값을 기준으로 나누어진 두 영역을 예측하는 모습이 됩니다.
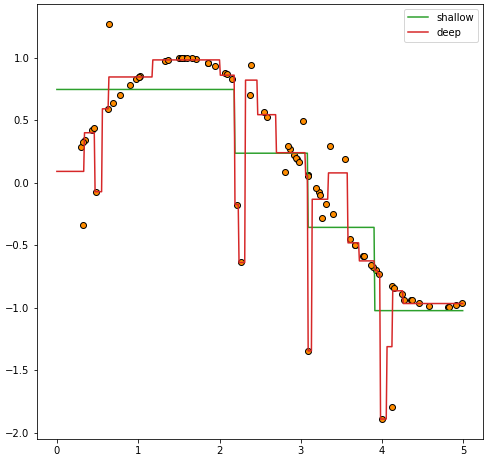
Depth에 따른 변화
shallow_depth_tree = DecisionTreeRegressor(max_depth=2)
deep_depth_tree = DecisionTreeRegressor(max_depth=5)
shallow_depth_tree.fit(data, label)
deep_depth_tree.fit(data, label)
shallow_pred = shallow_depth_tree.predict(viz_test_data)
deep_pred = deep_depth_tree.predict(viz_test_data)
plt.figure(figsize=(8, 8))
plt.scatter(data, label, edgecolor="black", c="darkorange")
plt.plot(viz_test_data, shallow_pred, color="C2", label="shallow")
plt.plot(viz_test_data, deep_pred, color="C3", label="deep")
plt.legend()위 코드에서는 max_depth 매개변수를 조정하여 Decision Tree Regressor 모델의 깊이(depth)에 따른 예측 결과를 비교하고 있습니다.
max_depth 매개변수는 Decision Tree의 최대 깊이를 설정하는 매개변수로, 모델의 복잡도를 조절하는 데 사용됩니다. max_depth 값을 작게 설정하면 모델은 보다 간단해지고 과적합을 방지할 수 있지만, 훈련 데이터의 복잡한 패턴을 모델링하는 데는 제한을 받습니다. 반대로, max_depth 값을 크게 설정하면 모델의 복잡도는 증가하지만, 훈련 데이터에 과적합할 가능성이 있습니다.
위 코드에서는 max_depth 값을 2와 5로 각각 설정하여 Decision Tree 모델을 학습시키고, 학습된 모델을 이용하여 테스트 데이터를 예측한 결과를 시각화하고 있습니다. 두 모델 모두 학습 데이터의 패턴을 어느 정도 따라가면서 테스트 데이터를 예측하고 있으나, max_depth 값이 큰 모델일수록 학습 데이터에 더욱 따라갑니다. 이는 max_depth 값이 커질수록 모델이 더 복잡해져서, 학습 데이터에 과적합하기 쉬워지기 때문입니다.