의사결정나무(Decision Tree) 정의 : 의사 결정 규칙과 그 결과물들을 트리 구조로 도식화한 것
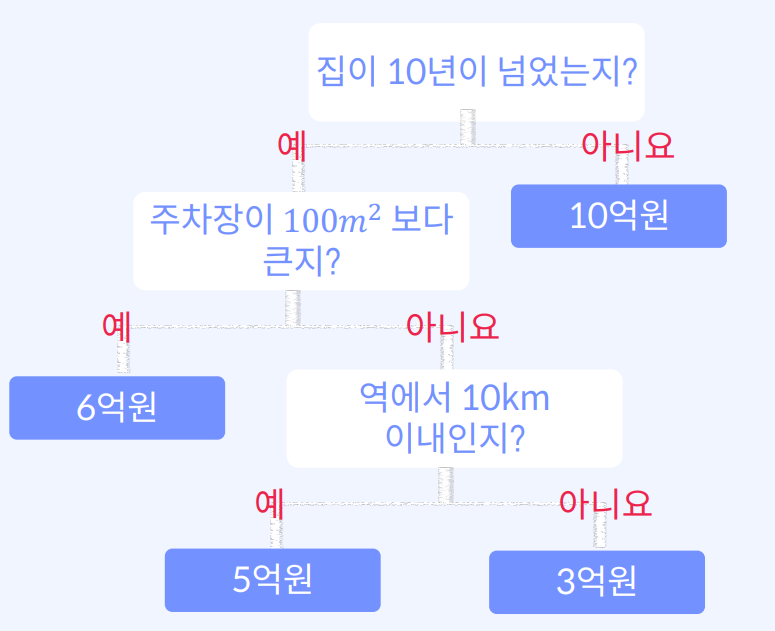
즉, 의사결정나무(Decision Tree)는 데이터 분석과 머신 러닝에서 많이 사용되는 분류 및 예측 모델 중 하나입니다. 이는 그래프 형태로 구성된 모델로, 각 분기점에서 가능한 선택 사항을 고려하여 데이터를 분류하거나 예측합니다.
의사결정나무는 루트 노드(root node)에서 시작하여, 각 분기점마다 하위 분기점(자식 노드)으로 나뉘어지며, 각 분기점에서는 하나의 특성(Feature)을 선택하여 이를 기준으로 데이터를 분류합니다. 이렇게 분류된 데이터는 다시 하위 분기점으로 이동하면서 분류 과정이 계속되어 최종적으로 하나의 결과(결정, 예측)를 도출합니다.
의사결정나무는 직관적이고 해석하기 쉽기 때문에, 데이터 분석에서 많이 활용되며, 또한 다른 머신 러닝 모델의 기본 요소로 사용됩니다
의사결정나무(Decision Tree)의 요소
1. 뿌리 마디
- 나무 구조가 시작되는 마디
- 전체 데이터로 이루어져 있다
- 중간 마디
- 나무 구조의 중간에 있는 마디들
- 끝 마디
- 나무 구조의 끝에 위치하는 마디들
- 끝 마디에서는 더 이상 노드가 생성되지 않음
- 깊이
- 뿌리 노드에서 끝 마디까지의 노드 개수
다시 정리해보면,
뿌리 마디(Root node): 의사결정나무의 시작점으로, 가장 상위에 위치한 마디입니다. 모든 분기점은 뿌리 마디에서부터 시작됩니다.
중간 마디(Intermediate node): 뿌리 마디를 제외한 나머지 분기점을 말합니다. 각 중간 마디는 하나의 특성(Feature)을 기준으로 데이터를 분류합니다.
끝 마디(Leaf node): 분류 결과가 도출되는 마디로, 더 이상 분기하지 않고 결정이 이루어지는 지점입니다.
깊이(Depth): 의사결정나무에서 가장 긴 분기 경로의 길이를 의미합니다. 깊이가 깊을수록 의사결정나무의 복잡도가 높아지며, 이는 과적합(Overfitting) 문제를 유발할 수 있습니다.
의사결정나무에서 사용되는 알고리즘
-> CART (Classification And Regression Tree) 알고리즘
- 목적: 각 분할에서 정보 이득을 최대화 하는 것
- 정보 이득의 최대화 -> 불순도의 감소
즉,
CART 알고리즘은 분류(Classification)와 회귀(Regression) 문제 모두를 해결할 수 있는 유연한 알고리즘으로, 각 분할에서 정보 이득을 최대화하는 것이 목적입니다. 정보 이득을 최대화하는 것은 분기 전후의 불순도 차이(impurity decrease)를 최대화하는 것을 의미합니다.
불순도란, 분류하려는 데이터 집합에서 서로 다른 클래스(범주)가 섞여 있는 정도를 나타내는 지표로, CART 알고리즘에서는 지니 계수(Gini index)를 사용합니다. 지니 계수는 0에서 1 사이의 값을 가지며, 0이면 해당 데이터 집합에서 모든 데이터가 동일한 클래스로 구성되어 있음을 나타내고, 1이면 해당 데이터 집합에서 모든 데이터가 서로 다른 클래스로 구성되어 있음을 나타냅니다.
CART 알고리즘은 데이터를 반복적으로 분할하면서 트리를 생성하며, 각 분기점에서는 가능한 모든 분할 후보군 중에서 지니 계수가 최소화되는 분할 방법을 선택합니다. 이렇게 생성된 의사결정나무는 각 분류 및 예측 문제에 대해 높은 정확도와 해석력을 제공합니다.
- 분할
노드에서 데이터가 어떤 기준에 의해 나눠지는 과정
즉, 의사결정나무의 노드에서 데이터가 어떤 기준에 의해 나눠지는 과정
- 정보 이득 Information Gain (또는 불순도 Impurity)
정답이 범주형 변수인 경우
1) 엔트로피 지수
2) 지니 지수
정답이 연속형 변수인 경우
1) MSE를 이용한 분산량 감소
즉, 정보 이득은 각 분할에서 분할 전후의 엔트로피 차이(또는 불순도 차이)를 의미하며, 정보 이득이 클수록 분할이 좋다는 것을 나타냅니다.
정답이 범주형 변수인 경우, 의사결정나무에서는 엔트로피 지수 또는 지니 지수를 사용하여 정보 이득을 계산합니다. 엔트로피 지수는 불확실성을 나타내는 지표로, 해당 변수가 갖는 값의 불균형성이 클수록 높은 값을 가지게 됩니다. 지니 지수는 0부터 1 사이의 값을 가지며, 0에 가까울수록 해당 변수가 잘 분류되어 있다는 것을 의미합니다.
정답이 연속형 변수인 경우, 의사결정나무에서는 평균 제곱 오차(Mean Squared Error, MSE)를 이용한 분산량 감소를 사용하여 정보 이득을 계산합니다. 분산량 감소는 해당 변수를 기준으로 데이터를 분할한 후, 각 분할의 분산량을 계산하여 분산량이 가장 많이 감소하는 지점을 선택합니다.
엔트로피 (Entropy)
정보 이론에서, 정보의 불확실함의 정도를 나타내는 양.
데이터를 잘 구분할 수 없을 수록 엔트로피는 커진다.
정보 이득의 최대화 -> 불순도의 감소 -> 엔트로피의 감소
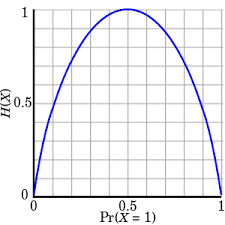
즉,
엔트로피(Entropy)는 정보 이론에서, 어떤 정보의 불확실성의 정도를 나타내는 양입니다. 엔트로피가 낮을수록, 해당 정보가 더욱 명확하고 예측 가능합니다. 엔트로피는 물리학에서 열역학 제 2 법칙에서 유래한 개념으로, 열역학적 계의 무질서함을 나타내는 양으로도 사용됩니다.
의사결정나무에서는 엔트로피를 분기 기준으로 사용하여 정보 이득을 계산합니다. 엔트로피의 값은 0부터 1 사이의 값을 가지며, 0에 가까울수록 해당 변수가 분류하는 범주가 균등하게 나뉘어져 있고, 1에 가까울수록 분류가 불균형합니다.
따라서 의사결정나무에서 정보 이득을 최대화하기 위해서는, 분기 전의 엔트로피보다 분기 후의 엔트로피가 작아지는 방향으로 분기 기준을 찾아야 합니다. 이를 위해 각 분기 후의 엔트로피 차이를 계산하여 정보 이득을 구하고, 정보 이득이 가장 큰 분기 기준을 선택합니다.
엔트로피 지수(Entropy Index) 수식

지니 지수 (Gini Index)
불평등의 정도를 나타내는 통계학적 지수
데이터가 비슷하게 있을 수록 지니 지수는 높아짐
정보 이득의 최대화 -> 불순도의 감소 -> 지니 지수 감소
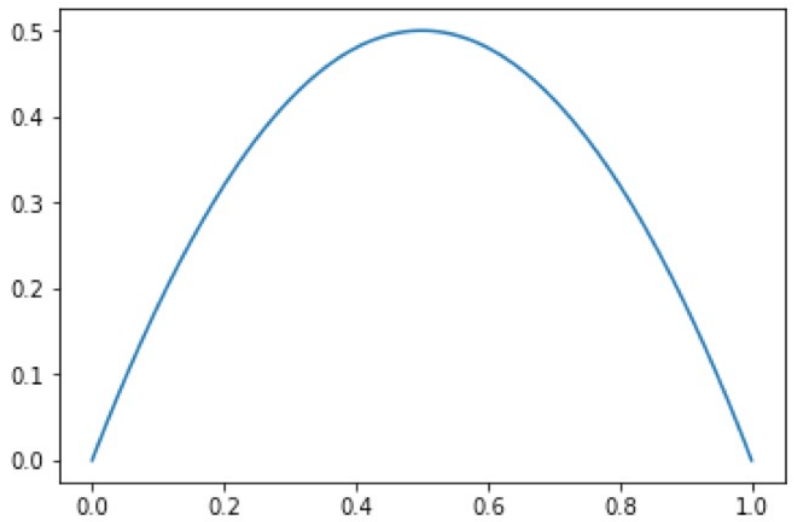
즉, 지니 지수는 엔트로피와 마찬가지로 불순도의 정도를 나타내는 지수입니다. 엔트로피와는 다르게, 지니 지수는 데이터가 어떻게 분포되어 있는지에 대한 정보도 포함하고 있습니다. 따라서, 엔트로피보다 더 강력한 특성을 가지고 있습니다.
지니 지수는 0에서 1사이의 값을 가지며, 0일 경우 모든 데이터가 동일한 범주에 속하는 경우입니다. 반면, 1일 경우, 데이터가 모든 범주에 골고루 분포되어 있는 균등한 상태를 의미합니다. 의사결정나무에서는, 각 분기마다 지니 지수가 가장 작은 변수를 선택하여 분기 기준으로 삼습니다. 지니 지수가 작을수록, 분기 후에 불순도의 감소가 더 크기 때문입니다.
지니 지수도 엔트로피와 마찬가지로, 분기 기준이 너무 많거나 불균형하게 나뉘어져 있을 때, 과적합이 발생할 수 있습니다. 따라서, 엔트로피와 마찬가지로, 적절한 분기 기준을 선택하거나 가지치기 등의 방법을 사용하여 모델을 단순화하는 것이 중요합니다.
지니 지수 수식

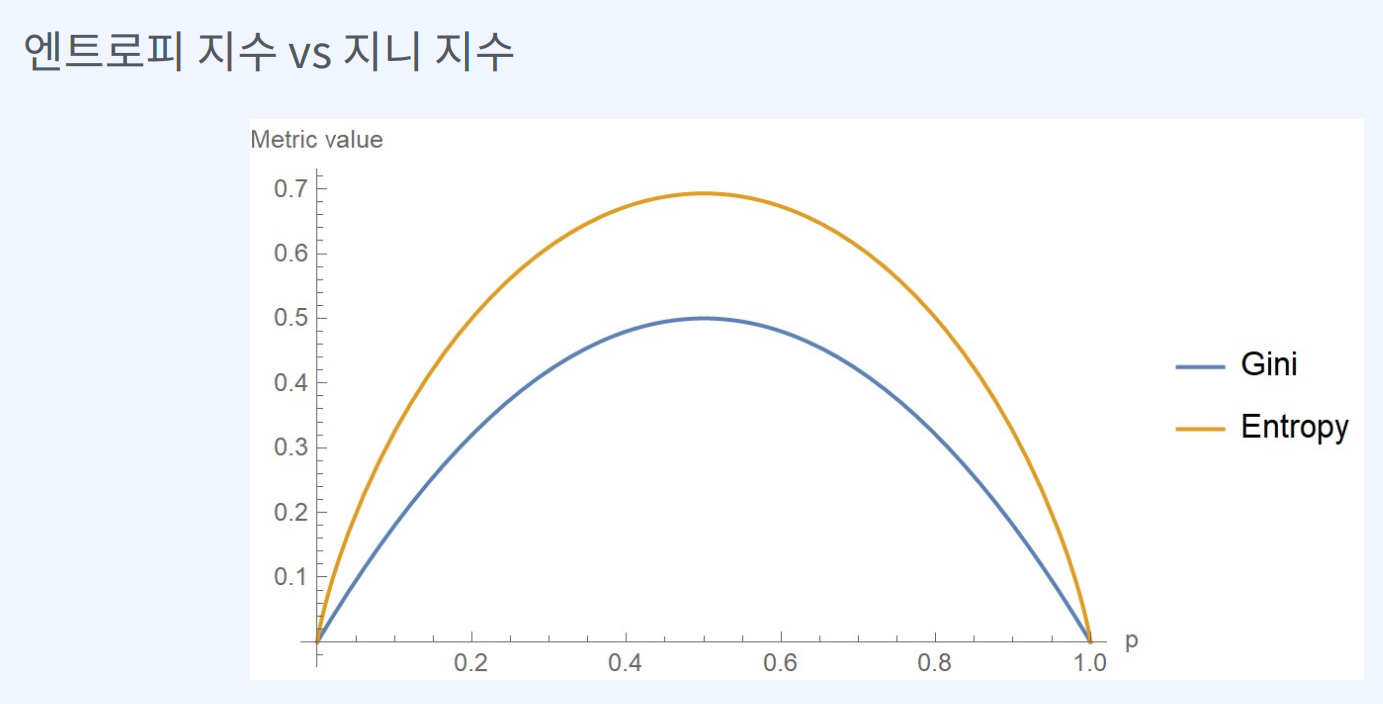
엔트로피 지수와 지니 지수는 모두 의사결정나무에서 사용되는 분기 기준으로, 불순도의 정도를 나타내는 지수입니다. 둘 다 값이 작을수록 불순도가 적다는 것을 의미하며, 정보 이득을 최대화하여 분기 기준을 선택하는데 사용됩니다. 하지만 엔트로피 지수와 지니 지수는 몇 가지 차이점이 있습니다.
첫째, 엔트로피 지수는 정보 이론에서 온 개념으로, 정보의 불확실함의 정도를 나타내는 지수입니다. 엔트로피는 각 클래스에 대한 확률을 가중치로 하여 계산되며, 분류 정확도를 높이는 것을 목적으로 합니다.
반면, 지니 지수는 불평등의 정도를 나타내는 통계학적 지수입니다. 지니 지수는 엔트로피와 마찬가지로 값이 작을수록 불순도가 적다는 것을 의미하지만, 데이터의 분포에 대한 정보도 포함하고 있습니다. 따라서, 데이터가 어떻게 분포되어 있는지에 따라서는 지니 지수가 엔트로피보다 더 효과적일 수 있습니다.
둘째, 엔트로피 지수는 로그 함수를 사용하기 때문에 계산 비용이 지니 지수에 비해 높습니다. 따라서, 데이터가 매우 큰 경우에는 지니 지수를 사용하는 것이 더 효율적입니다.
결론적으로, 엔트로피 지수와 지니 지수는 모두 분기 기준으로 사용될 수 있으며, 어떤 지수를 선택할지는 데이터의 특성과 목적에 따라 다를 수 있습니다. 일반적으로는 두 지수를 모두 사용하여 비교하고, 더 나은 결과를 내는 지수를 선택하는 것이 바람직합니다.
노드를 나누는 방법
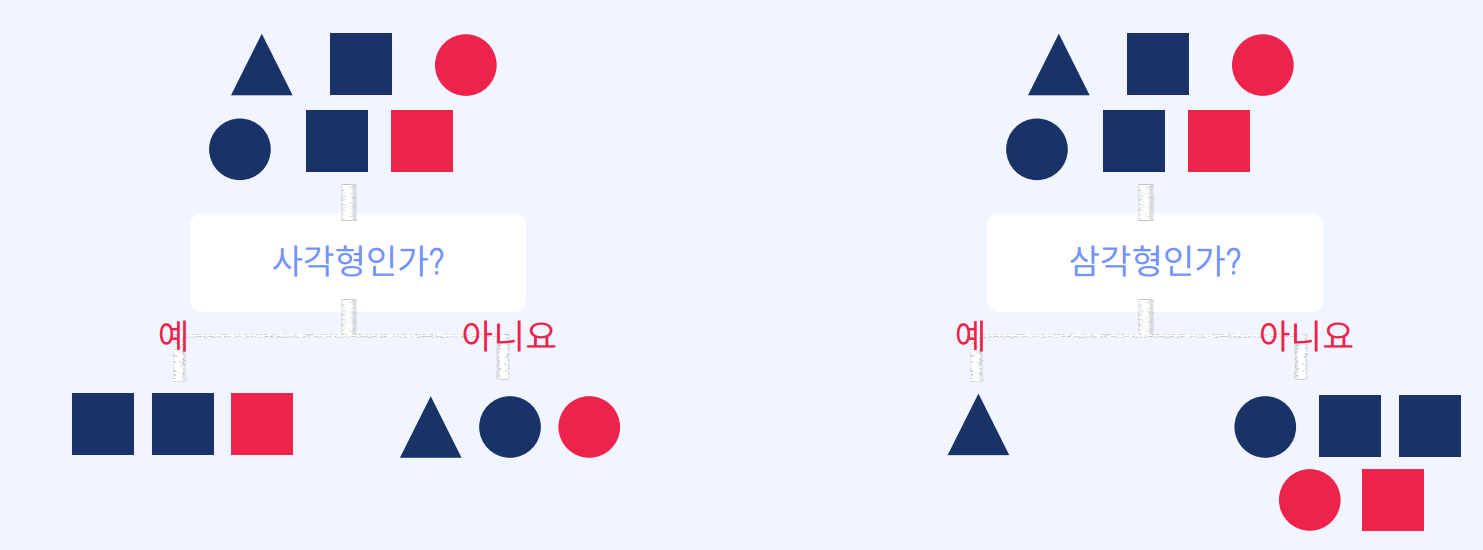
1. 범주형 변수
- 데이터의 특성의 유무로 분할을 한다.
- 정보 이득을 최대화 하는 분할을 선택한다
- 연속형 변수
- 특성의 유무로 나눌 수 없다.
- 경계값을 찾고 경계값과의 비교를 통해 데이터를 분할한다.
즉, 연속형 변수의 경우, 해당 특성 값이 특정 임계값보다 큰지 작은지에 따라 데이터를 분할할 수 있습니다. 임계값은 선택한 분할 기준에 따라 정보 이득을 최대화하거나 불순도를 최소화하는 값을 찾아서 결정합니다.
연속형 변수의 경계값을 찾는 방법
1. 변수 값에 따라 데이터를 정렬한다.
2. 정답이 바뀌는 경계 지점을 찾는다.
3. 경계의 평균값을 기준으로 잡는다.
4. 구간별 경계값을 기준으로 불순도를 계산한다.
5. 가장 불순도를 낮추는구간을 경계로 나눈다
Feature Importance (변수 중요도)
- 의사결정나무에서 어떤 변수가 가장 중요한지를 나타내는 정도
- 불순도를 가장 크게 감소시키는 변수의 중요도가 가장 크다
- 불순도의 감소는 정보 이득의 최대화와 동일한 뜻
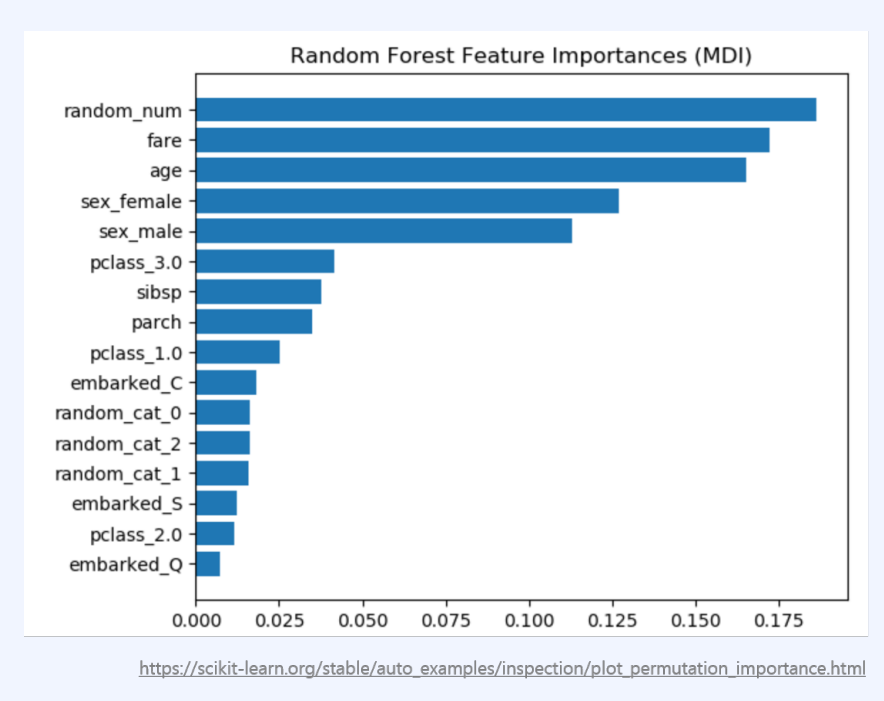
지니 지수를 이용한 Feature Importance
지니 중요도(Gini Importance)는 변수별로 해당 변수를 이용하여 분기하는 모든 노드에서의 Gini Index 차이의 평균값을 계산하여 변수의 중요도를 측정한다.
지니 중요도(feature i) = ∑(분기 j에서의 샘플 수 / 전체 샘플 수) x (Gini Index(feature i) - Gini Index(분기 j에서 feature i 미포함))
여기서 Gini Index(feature i)는 feature i를 사용하여 분기를 나눌 때의 지니 지수를 의미하며, Gini Index(분기 j에서 feature i 미포함)은 feature i를 사용하지 않고 분기를 나눌 때의 지니 지수를 의미합니다. 즉, 각 분기에서 해당 변수를 사용했을 때와 사용하지 않았을 때의 지니 지수 차이를 구한 뒤, 이를 해당 변수의 분기 수로 가중평균하여 변수의 중요도를 계산합니다.




Full Tree
- 모든 끝 마디에서의 순도가 100%인 상태
- 분기가 너무 많아서 과대 적합(Overfitting) 위험이 발생할 수 있음
가지 치기
- 분기가 너무 많아지는 것을 막기 위해서 적절한 수준에서 끝 노드를 결합해주는 것
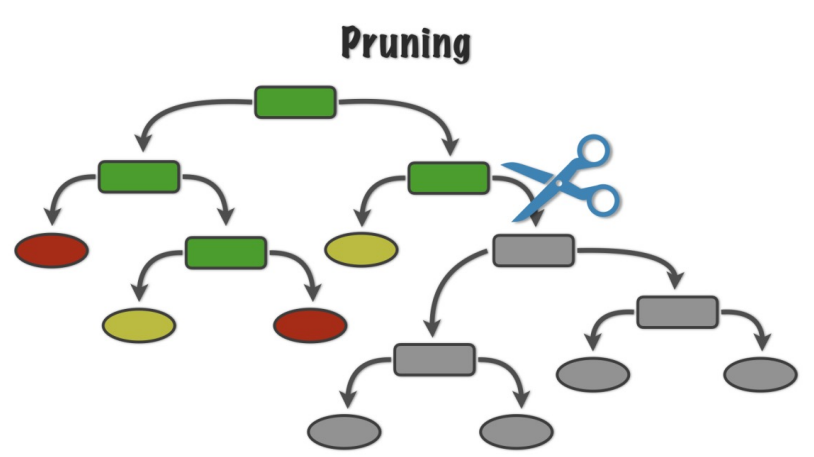
- 사전 가지치기 (Pre-Pruning)
의사결정나무의 최대 Depth나 노드의 최소 개수를 미리 지정해 더 이상의 분할이 일어나지 않게 하는 방법 - 사후 가지치기 (Post-Pruning)
의사결정나무를 만든 후 데이터가 적은 노드를 삭제 or 병합
1) 장점
- 모델의 예측 결과를 해석하고 이해하기 쉽다. (if … then …)
- 데이터를 가공할 필요가 거의 없다.
2) 단점
- 연속형 변수를 범주형 값으로 취급하기 때문에 분리의 경계점 부근에서 예측 오류가 클 수 있다.
- 노이즈 데이터에 영향을 크게 받는다.
-> Overfitting 문제가 발생하기 쉽다
