Iris의 종류 분류(Multiclass)
이번에는 Class가 여러개인 데이터를 Logistic Regression으로 예측해 보겠습니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)Data Load - 데이터는 sklearn.datasets 의 load_iris 함수를 이용해 받을 수 있습니다.
from sklearn.datasets import load_iris
iris = load_iris()데이터에서 사용되는 변수는 암술과 수술의 길이와 넓이입니다.
아래는 변수 목록!
sepal length (cm)
sepal width (cm)
petal length (cm)
petal width (cm)
iris["feature_names"] #정답은 iris 꽃의 종류입니다.
iris["target_names"]
data, target = iris["data"], iris["target"]
target


전체 코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
from sklearn.datasets import load_iris
iris = load_iris()
print(iris["feature_names"]) #정답은 iris 꽃의 종류입니다.
print(iris["target_names"])
data, target = iris["data"], iris["target"]
print(target)위 코드는 Python 프로그래밍 언어를 사용하여 데이터 분석 및 시각화를 위한 라이브러리인 pandas, numpy, matplotlib.pyplot을 불러오고, 사이킷런(Scikit-learn) 라이브러리에서 제공하는 iris(붓꽃) 데이터셋을 불러오는 코드입니다.
np.random.seed(2021) : np.random 모듈에서 사용되는 시드값(seed)을 2021로 설정하여, 난수(random number) 생성 시 항상 같은 값을 반환하도록 합니다.
load_iris() : 사이킷런에서 제공하는 iris 데이터셋을 불러오는 함수입니다.
iris["feature_names"] : iris 데이터셋의 열(column) 이름, 즉 꽃잎과 꽃받침의 길이와 너비를 나타내는 feature(특징)의 이름을 출력합니다.
iris["target_names"] : iris 데이터셋의 붓꽃 종류의 이름을 출력합니다.
data, target = iris["data"], iris["target"] : iris 데이터셋에서 feature(특징)과 target(목표) 데이터를 변수 data와 target에 각각 저장합니다.
target : iris 데이터셋에서 붓꽃의 종류를 나타내는 target(목표) 데이터를 출력합니다. 이 데이터는 0, 1, 2의 값을 가지며 각각 setosa, versicolor, virginica 종을 나타냅니다.
데이터 EDA - 데이터의 분포를 확인하면 다음과 같습니다.
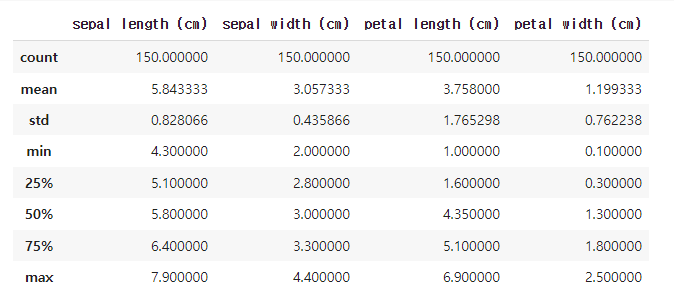
pd.DataFrame(data, columns=iris["feature_names"]).describe()위 코드는 pandas DataFrame을 사용하여 iris 데이터셋에서 feature 데이터를 columns에 저장하고, describe() 메소드를 사용하여 기술통계를 계산하는 코드입니다.
pd.DataFrame(data, columns=iris["feature_names"]) : iris 데이터셋의 feature 데이터를 columns에 저장하여 DataFrame 형태로 변환합니다.
describe() : DataFrame의 열(column) 별로 기술통계(descriptive statistics)를 계산하여 출력합니다. 기술통계는 각 열의 개수(count), 평균(mean), 표준편차(standard deviation), 최소값(minimum), 25%, 50%, 75% 분위수, 최대값(maximum)을 계산합니다.
즉, 위 코드는 iris 데이터셋에서 feature 데이터를 DataFrame으로 변환한 후, 각 feature(특징)의 기술통계 정보를 출력합니다. 이 정보는 데이터 분석에서 중요한 역할을 하며, 데이터의 분포와 특징을 파악하는 데 도움을 줍니다.
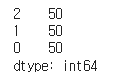
정답의 종류별 개수는 다음과 같습니다.
pd.Series(target).value_counts()위 코드는 pandas Series를 사용하여 iris 데이터셋에서 target 데이터를 Series 형태로 변환하고, value_counts() 메소드를 사용하여 각 붓꽃 종류별로 데이터의 개수를 계산하는 코드입니다.
pd.Series(target) : iris 데이터셋의 target 데이터를 Series 형태로 변환합니다.
value_counts() : Series 내의 고유한(unique) 값들의 개수를 계산하여 출력합니다. 즉, iris 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산합니다.
따라서, 위 코드는 iris 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산한 결과를 출력합니다. 이 정보는 데이터셋의 클래스 분포(class distribution)를 파악하는 데 도움을 줍니다.
Data Split - 데이터를 train과 test로 나누겠습니다.
from sklearn.model_selection import train_test_split
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021
)
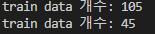
print("train data 개수:", len(train_data))
print("train data 개수:", len(test_data))위 코드는 사이킷런에서 제공하는 train_test_split() 함수를 사용하여 iris 데이터셋에서 전체 데이터를 train 데이터와 test 데이터로 나누는 코드입니다.
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021
)
train_test_split() : 전체 데이터를 train 데이터와 test 데이터로 나누는 함수입니다. 매개변수로 전체 데이터(data)와 target 데이터(target)를 입력하고, train 데이터의 비율(train_size)과 난수 생성 시 사용되는 시드값(random_state)을 설정할 수 있습니다. 이 함수는 train 데이터와 test 데이터를 각각 feature 데이터(train_data, test_data)와 target 데이터(train_target, test_target)로 반환합니다.
위 코드에서는 전체 데이터를 70% 비율로 train 데이터와 30% 비율로 test 데이터로 나누었습니다.
print("train data 개수:", len(train_data)) : train 데이터의 개수를 출력합니다.
print("test data 개수:", len(test_data)) : test 데이터의 개수를 출력합니다.
따라서, 위 코드는 iris 데이터셋에서 전체 데이터를 70% 비율로 train 데이터와 30% 비율로 test 데이터로 나눈 후, 각 데이터의 개수를 출력합니다. 이 과정은 데이터 분석 및 모델 학습 시에 데이터를 train과 test로 나누어 overfitting을 방지하고, 모델의 성능을 검증하는 데 도움을 줍니다.
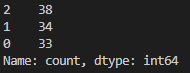
Train 데이터의 정답 개수를 보면 아래와 같습니다.
pd.Series(train_target).value_counts()위 코드는 pandas Series를 사용하여 train 데이터셋에서 target 데이터를 Series 형태로 변환하고, value_counts() 메소드를 사용하여 각 붓꽃 종류별로 train 데이터의 개수를 계산하는 코드입니다.
pd.Series(train_target) : train 데이터셋의 target 데이터를 Series 형태로 변환합니다.
value_counts() : Series 내의 고유한(unique) 값들의 개수를 계산하여 출력합니다. 즉, train 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산합니다.
따라서, 위 코드는 train 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산한 결과를 출력합니다. 이 정보는 train 데이터셋의 클래스 분포(class distribution)를 파악하는 데 도움을 줍니다.
Test 데이터의 정답 개수를 보면 아래와 같습니다.
pd.Series(test_target).value_counts()위 코드는 pandas Series를 사용하여 test 데이터셋에서 target 데이터를 Series 형태로 변환하고, value_counts() 메소드를 사용하여 각 붓꽃 종류별로 test 데이터의 개수를 계산하는 코드입니다.
pd.Series(test_target) : test 데이터셋의 target 데이터를 Series 형태로 변환합니다.
value_counts() : Series 내의 고유한(unique) 값들의 개수를 계산하여 출력합니다. 즉, test 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산합니다.
따라서, 위 코드는 test 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산한 결과를 출력합니다. 이 정보는 test 데이터셋의 클래스 분포(class distribution)를 파악하는 데 도움을 줍니다.
그런데 단순히 데이터를 분류할 경우 원래 데이터의 target 분포를 반영하지 못합니다.
이때 사용하는 것이 startify 옵션입니다.
이 옵션에 데이터의 label을 넣어주면 원본 데이터의 정답 분포를 반영해 데이터를 나눠줍니다.
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021, stratify=target
)
pd.Series(train_target).value_counts()
pd.Series(test_target).value_counts()위 코드는 train_test_split() 함수의 stratify 매개변수를 이용하여 데이터를 분할할 때, target 데이터의 비율을 유지하도록 하는 코드입니다. 이를 통해 train 데이터와 test 데이터의 분포가 불균형하게 되는 것을 방지할 수 있습니다.
train_test_split() 함수에서 stratify 매개변수를 target으로 설정하여 전체 데이터의 target 데이터의 분포를 유지하도록 설정하였습니다.
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021, stratify=target
)
pd.Series(train_target).value_counts() : train 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산하여 출력합니다.
pd.Series(test_target).value_counts() : test 데이터셋에서 붓꽃 종류별로 데이터의 개수를 계산하여 출력합니다.
위 코드에서는 분할된 train 데이터셋과 test 데이터셋에서 각각 붓꽃 종류별로 데이터의 개수를 계산하여 출력합니다. 이를 통해 stratify를 적용하여 데이터를 분할하였을 때, 각 데이터셋에서 붓꽃 종류별로 데이터의 분포가 유지되는 것을 확인할 수 있습니다.
즉, 지금까지의 전체 코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
#데이터 로드
iris = load_iris()
data, target = iris["data"], iris["target"]
#데이터셋의 기초 통계량 확인
pd.DataFrame(data, columns=iris["feature_names"]).describe()
#붓꽃 종류별 데이터 개수 확인
pd.Series(target).value_counts()
#데이터 분할
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021, stratify=target
)
#train 데이터셋에서 붓꽃 종류별 데이터 개수 확인
print(pd.Series(train_target).value_counts())
#test 데이터셋에서 붓꽃 종류별 데이터 개수 확인
print(pd.Series(test_target).value_counts())Multiclass
: 여러 개의 클래스 중에서 하나를 선택하는 문제를 의미합니다. 즉, 예측하고자 하는 대상이 2개 이상의 클래스 중에서 하나일 경우에 해당
예를 들어, 붓꽃의 품종을 예측하는 문제는 세 가지의 품종 중 하나를 선택하는 Multiclass 문제입니다. 이와 같은 문제를 해결하기 위해 로지스틱 회귀, 의사결정 나무, SVM 등의 알고리즘이 사용될 수 있습니다.
from sklearn.linear_model import LogisticRegression시각화를 위해서 Sepal length와 Sepal width만 사용하겠습니다.
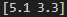
X = train_data[:, :2]
X[0]위 코드는 train 데이터셋에서 2개의 feature(꽃받침 길이와 꽃받침 폭)만을 선택하여 X 변수에 저장하는 코드입니다. 이를 위해 train_data 변수에서 첫번째 차원(행)의 모든 데이터를 선택한 후, 그 중에서 첫번째 feature(꽃받침 길이)와 두번째 feature(꽃받침 폭)만을 선택하였습니다.
X[0]은 선택된 feature 중 첫번째 데이터(즉, 첫번째 꽃의 꽃받침 길이와 폭)를 출력하는 코드입니다.
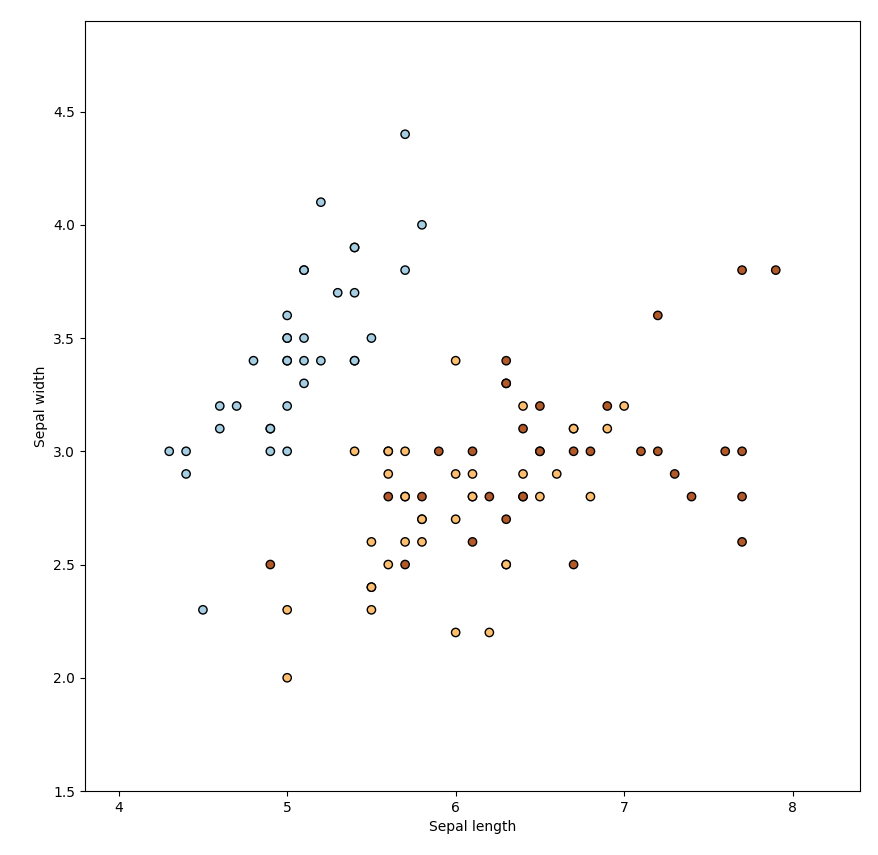
데이터를 시각화하면 다음과 같이 그려집니다.
plt.figure(1, figsize=(10, 10))
plt.scatter(X[:, 0], X[:, 1], c=train_target, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(X[:,0].min()-0.5, X[:,0].max()+0.5)
plt.ylim(X[:,1].min()-0.5, X[:,1].max()+0.5)위 코드는 scatter plot을 그리는 코드입니다.
plt.figure(1, figsize=(10, 10)): 그림을 그리기 위한 Figure 객체를 생성합니다. figsize는 그림의 크기를 설정합니다.
plt.scatter(X[:, 0], X[:, 1], c=train_target, edgecolors='k', cmap=plt.cm.Paired): X 배열의 첫 번째 열과 두 번째 열을 각각 x축과 y축으로 설정하고, 각 점의 색상은 train_target에 따라 다르게 설정합니다. edgecolors는 점의 테두리 색상을 설정하며, cmap은 색상 맵을 지정합니다.
plt.xlabel('Sepal length'): x축 라벨을 'Sepal length'로 설정합니다.
plt.ylabel('Sepal width'): y축 라벨을 'Sepal width'로 설정합니다.
plt.xlim(X[:,0].min()-0.5, X[:,0].max()+0.5): x축 범위를 X 배열의 첫 번째 열에서 최솟값에서 0.5를 뺀 값부터 최댓값에서 0.5를 더한 값까지로 설정합니다.
plt.ylim(X[:,1].min()-0.5, X[:,1].max()+0.5): y축 범위를 X 배열의 두 번째 열에서 최솟값에서 0.5를 뺀 값부터 최댓값에서 0.5를 더한 값까지로 설정합니다.
따라서 위 코드는 꽃받침 길이와 폭에 따라 점으로 데이터를 나타내고, 붓꽃 종류(train_target)에 따라 색상이 다른 scatter plot을 그리는 코드입니다.
One vs Rest
우선 One vs Rest 방법의 Logistic Regression을 학습해 보겠습니다.
먼저, one vs Rest (OvR)란, 다중 분류(multiclass classification) 문제를 이진 분류(binary classification) 문제로 바꾸어 해결하는 방법 중 하나입니다.
OvR은 각 클래스마다 해당 클래스와 나머지 클래스를 구분하는 이진 분류 문제를 푸는 방법입니다. 예를 들어, 세 개의 클래스가 있는 다중 분류 문제에서, 첫 번째 클래스를 분류하기 위해서는 첫 번째 클래스와 두 번째, 세 번째 클래스를 구분하는 이진 분류 문제를 푸는 것입니다. 이를 나머지 클래스에 대해서도 반복하여 모든 클래스에 대해 이진 분류 모델을 만들고, 이진 분류 모델의 예측 결과를 종합하여 최종 클래스를 결정합니다.
OvR은 각 클래스를 독립적으로 분류하기 때문에 계산이 간단하고 적용하기 쉽습니다. 또한, 클래스 수가 많을 경우에도 적용할 수 있어 다중 분류 문제에 유용합니다. 하지만, 클래스의 수가 많아질수록 각 클래스와 나머지 클래스를 구분하기 위한 이진 분류 문제의 수가 많아지므로 모델의 성능이 감소할 수 있습니다.
ovr_logit = LogisticRegression(multi_class="ovr")
ovr_logit.fit(X, train_target)
x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
plt.figure(1, figsize=(10, 10))
plt.scatter(X[:, 0], X[:, 1], c=ovr_logit.predict(X), edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
ovr_logit = LogisticRegression(multi_class="ovr")
ovr_logit.fit(X, train_target)
x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
plt.figure(1, figsize=(10, 10))
plt.scatter(X[:, 0], X[:, 1], c=ovr_logit.predict(X), edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
ovr_logit = LogisticRegression(multi_class="ovr")
ovr_logit.fit(X, train_target)
x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
plt.figure(1, figsize=(10, 10))
plt.scatter(X[:, 0], X[:, 1], c=ovr_logit.predict(X), edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
coef = ovr_logit.coef_
intercept = ovr_logit.intercept_
def plot_hyperplane(c, color):
def line(x0):
return (-(x0 * coef[c, 0]) - intercept[c]) / coef[c, 1]
plt.plot([x_min, x_max], [line(x_min), line(x_max)],
ls="--", color=color)
for i, color in zip(ovr_logit.classes_, "bry"):
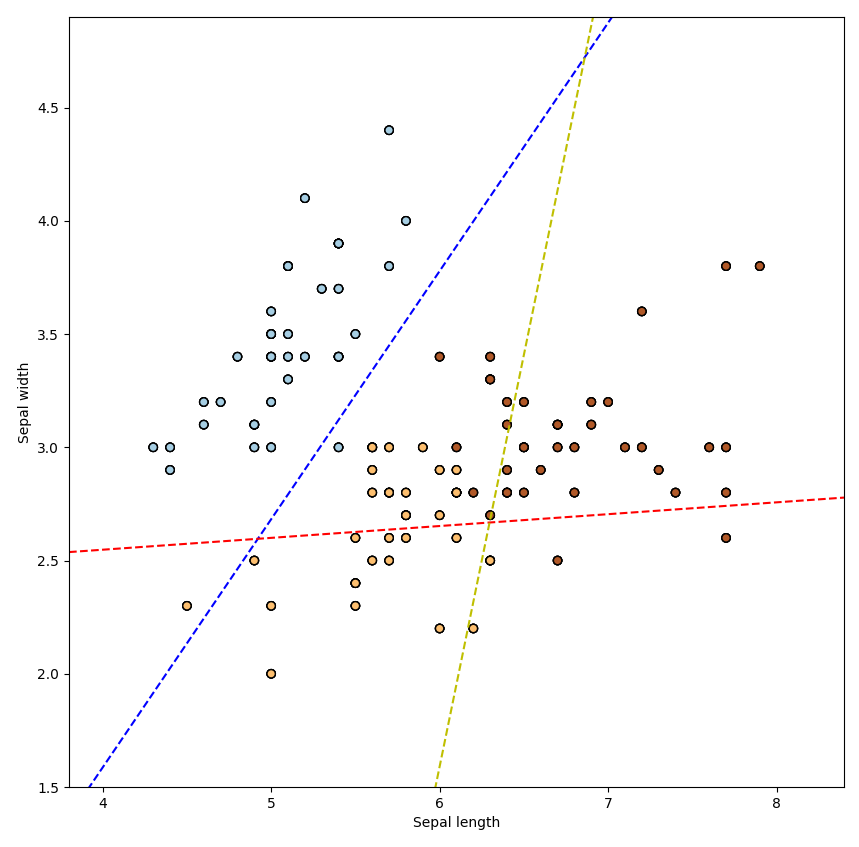
plot_hyperplane(i, color)이 코드는 sepal length와 sepal width 두 가지 feature를 가진 붓꽃 데이터셋을 이용해 One-vs-Rest(OvR) 방식으로 로지스틱 회귀 분류기를 학습한 뒤, 그 결과를 시각화하는 코드입니다.
먼저 LogisticRegression 모델을 multi_class="ovr" 옵션으로 초기화합니다. 이는 One-vs-Rest(OvR) 방식으로 다중 클래스 분류 문제를 해결하는 방법 중 하나입니다. 다중 클래스 분류 문제에서 OvR 방식은 각 클래스를 하나의 이진 분류 문제로 취급합니다. 즉, 각 클래스를 기준으로 해당 클래스에 속하는 샘플과 속하지 않는 샘플을 구분하는 이진 분류 문제를 여러 번 풀게 됩니다.
그 다음, 학습 데이터 X와 traintarget을 이용해 fit 메서드를 호출하여 모델을 학습합니다. ovr_logit.predict(X)를 통해 각 샘플의 예측 클래스를 구하고, scatter 함수를 이용해 산점도를 그리는데, 이 때 예측 결과에 따라 색을 다르게 표시합니다. 마지막으로 coef와 intercept_ 속성을 이용해 각 클래스를 분류하는 초평면(hyperplane)을 그립니다.
Multinomial
정답의 분포가 Multinomial 분포를 따른다고 가정한 후 시행하는 Multiclass Logistic Regression 입니다.
LogisticRegression의 기본 값은 "multinomial" 입니다.
즉, LogisticRegression의 multi_class 파라미터의 기본값은 "multinomial"입니다.
이 경우에는 다항 분류 문제를 해결하기 위해 cross-entropy loss를 사용하며, solver 파라미터를 "lbfgs"로 설정해야 합니다. 이 방식은 one-vs-rest 방식보다 분류 성능이 더 좋을 수 있습니다.
multi_logit = LogisticRegression(multi_class="multinomial")
multi_logit.fit(X, train_target)
x_min, x_max = X[:,0].min() - 0.5, X[:,0].max() + 0.5
y_min, y_max = X[:,1].min() - 0.5, X[:,1].max() + 0.5
plt.figure(1, figsize=(10, 10))
plt.scatter(X[:, 0], X[:, 1], c=multi_logit.predict(X), edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
coef = multi_logit.coef_
intercept = multi_logit.intercept_
def plot_hyperplane(c, color):
def line(x0):
return (-(x0 * coef[c, 0]) - intercept[c]) / coef[c, 1]
plt.plot([x_min, x_max], [line(x_min), line(x_max)],
ls="--", color=color)
for i, color in zip(multi_logit.classes_, "bry"):
plot_hyperplane(i, color)위 코드는 Multinomial Logistic Regression을 이용하여 붓꽃 데이터의 분류 결과를 시각화한 것입니다.
LogisticRegression 클래스를 호출할 때 multi_class 인자를 "multinomial"로 설정하여 Multinomial Logistic Regression을 선택하였습니다.
모델을 학습시키기 위해 fit() 메소드를 사용하였으며, X와 train_target을 인자로 전달하여 학습하였습니다.
그 후, 산점도를 그리기 위해 X[:, 0]와 X[:, 1]을 x, y축으로 설정하였고, c에 multi_logit.predict(X)를 대입하여 색깔을 지정하였습니다.
마지막으로, Multinomial Logistic Regression의 경계를 그리기 위해 모델의 계수(coef)와 절편(intercept)을 구하고, 이를 이용하여 plot_hyperplane() 함수를 정의하였습니다. 이 함수는 계수와 절편을 이용하여 경계를 계산하고, 이를 점선으로 그리는 역할을 합니다.
for 루프에서 multilogit.classes를 이용하여 분류 결과 클래스를 가져오고, 이를 바탕으로 경계를 그렸습니다. 각 클래스에 대해 다른 색상을 지정하여 시각적으로 구분할 수 있도록 하였습니다.
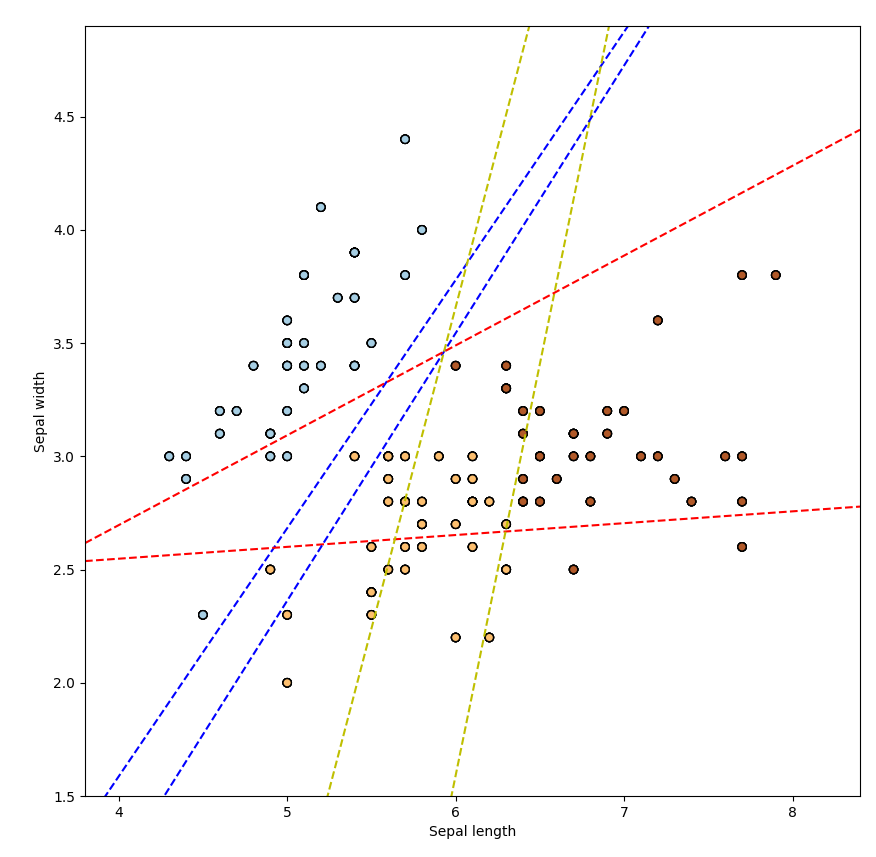
Logistic Regression (Multinomial)
multi_logit = LogisticRegression()
multi_logit.fit(train_data, train_target) #학습
train_pred_proba = multi_logit.predict_proba(train_data) #예측
sample_pred = train_pred_proba[0]
sample_pred
print(f"class 0에 속하지 않을 확률: {1 - sample_pred[0]:.4f}")
print(f"class 1과 2에 속할 확률: {sample_pred[1:].sum():.4f}")
train_pred = multi_logit.predict(train_data)
test_pred = multi_logit.predict(test_data)위의 코드는 Multinomial Logistic Regression을 사용하여 train_data에 대한 예측 확률을 계산한 뒤, 첫 번째 샘플에 대한 예측 확률을 출력하는 코드입니다.
다음으로, 첫 번째 샘플이 class 0에 속하지 않을 확률과 class 1 또는 class 2에 속할 확률을 출력합니다. 이때, class 0에 속하지 않을 확률은 1에서 첫 번째 예측 확률을 뺀 값으로 계산하고, class 1과 class 2에 속할 확률은 두 번째부터 마지막 예측 확률의 합으로 계산합니다.
마지막으로, 학습 데이터와 테스트 데이터에 대한 예측을 각각 train_pred와 test_pred 변수에 저장합니다.

평가
from sklearn.metrics import accuracy_score
train_acc = accuracy_score(train_target, train_pred)
test_acc = accuracy_score(test_target, test_pred)
print(f"Train accuracy is : {train_acc:.2f}")
print(f"Test accuracy is : {test_acc:.2f}")위 코드는 다중 클래스 분류 문제에서 로지스틱 회귀 분석을 수행하고, 학습된 모델의 성능을 평가하는 코드입니다.
먼저, LogisticRegression 클래스를 이용하여 다중 클래스 분류를 위한 모델 multi_logit을 학습시킵니다. fit() 메소드를 사용하여 학습 데이터인 train_data와 train_target을 이용하여 모델을 학습시킵니다.
다음으로, 학습된 모델 multi_logit을 이용하여 학습 데이터인 train_data의 예측값과 그 예측값의 확률 값을 구합니다. 이 때, predict_proba() 메소드를 사용합니다.
그 다음, sample_pred는 학습 데이터 중 첫 번째 샘플에 대한 예측값의 확률을 담고 있습니다. 이를 이용하여 해당 샘플이 클래스 0에 속하지 않을 확률과 클래스 1 또는 2에 속할 확률을 출력합니다.
마지막으로, accuracy_score() 함수를 사용하여 학습된 모델의 성능을 평가합니다. 이 함수는 실제 클래스와 예측된 클래스를 입력하면 정확도를 계산해줍니다. train_acc와 test_acc는 각각 학습 데이터와 테스트 데이터에 대한 정확도를 나타냅니다.

Logistic Regression (OVR)
Logistic Regression에서 OVR(One-vs-Rest)는 multi-class 분류 문제에서 사용되는 방법 중 하나입니다. OVR은 각각의 class를 기준으로 다른 모든 class와 구분하는 이진 분류(binary classification) 문제로 변환합니다. 예를 들어, 3개의 class(A, B, C)가 있는 경우, A를 기준으로 A vs. (B, C)로 나누고, B를 기준으로 B vs. (A, C)로 나누고, C를 기준으로 C vs. (A, B)로 나누어 각각 이진 분류 문제로 해결합니다.
OVR 방법은 모델이 각각의 클래스에 대해 이진 분류를 수행하기 때문에 각 클래스마다 하나의 분류 모델을 학습시키면 됩니다. 따라서, OVR 방법은 계산 비용이 적으며, 이진 분류 모델이 각 클래스의 경계를 어느 정도 잘 학습할 수 있다면 정확한 결과를 도출할 수 있습니다.
ovr_logit = LogisticRegression(multi_class="ovr")
ovr_logit.fit(train_data, train_target) #학습
ovr_train_pred = ovr_logit.predict(train_data) #예측
ovr_test_pred = ovr_logit.predict(test_data)
from sklearn.metrics import accuracy_score #평가
ovr_train_acc = accuracy_score(train_target, ovr_train_pred)
ovr_test_acc = accuracy_score(test_target, ovr_test_pred)
print(f"One vs Rest Train accuracy is : {ovr_train_acc:.2f}")
print(f"One vs Rest Test accuracy is : {ovr_test_acc:.2f}")해당 코드는 One-vs-Rest(OvR) Logistic Regression을 이용하여 붓꽃 데이터셋을 학습하고 평가하는 코드입니다. OvR 방식은 다중 클래스 분류 문제에서 각 클래스 별로 이진 분류 문제로 변환하여 해결하는 방법입니다.
코드를 간단히 설명하면, LogisticRegression 모델 객체를 multi_class="ovr"로 설정하여 OvR 방식으로 모델을 학습하고, 학습된 모델을 이용하여 train 데이터와 test 데이터의 예측값을 구합니다. 그리고 accuracy_score 함수를 사용하여 train 데이터와 test 데이터에 대한 분류 정확도를 계산합니다.
즉, OvR 방식은 각 클래스를 나머지 클래스들과 구분하여 이진 분류하는 방법으로 분류 모델을 학습하고, 다중 클래스 분류 문제를 해결하는 방법입니다.


