Logistic Regression으로 폐암의 양성 음성 분류
Data - 이번 실습에서 사용하는 데이터는 폐암의 양성, 음성 여부를 구분하는 문제입니다.
Data Load - 데이터는 sklearn.datasets 의 load_breast_cancer 함수를 이용해 받을 수 있습니다.
코드로 확인해보자!
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021) #numpy 라이브러리의 random 모듈을 사용하여 시드값을 설정
#scikit-learn 라이브러리의 datasets 모듈에서 load_breast_cancer 함수를 import
from sklearn.datasets import load_breast_cancer
#load_breast_cancer 함수를 사용하여 유방암 데이터셋을 불러온다.
cancer = load_breast_cancer()
#유방암 데이터셋에서 특징(feature)의 이름을 나타내는 배열을 출력
cancer["feature_names"]
결과값은 다음과 같다:
- cancer["feature_names"]: 유방암 데이터셋에서 30개의 특징(feature) 이름이 출력됩니다.
- cancer["target_names"]: 유방암 데이터셋에서 종류(target)의 이름이 "malignant"와 "benign"으로 출력됩니다.
- data[0]: 첫 번째 종양의 30개 특징(feature) 데이터가 출력됩니다.
- target[0]: 첫 번째 종양의 종류(target) 데이터가 0으로 출력됩니다. (즉, 양성 종양입니다.)
Data EDA
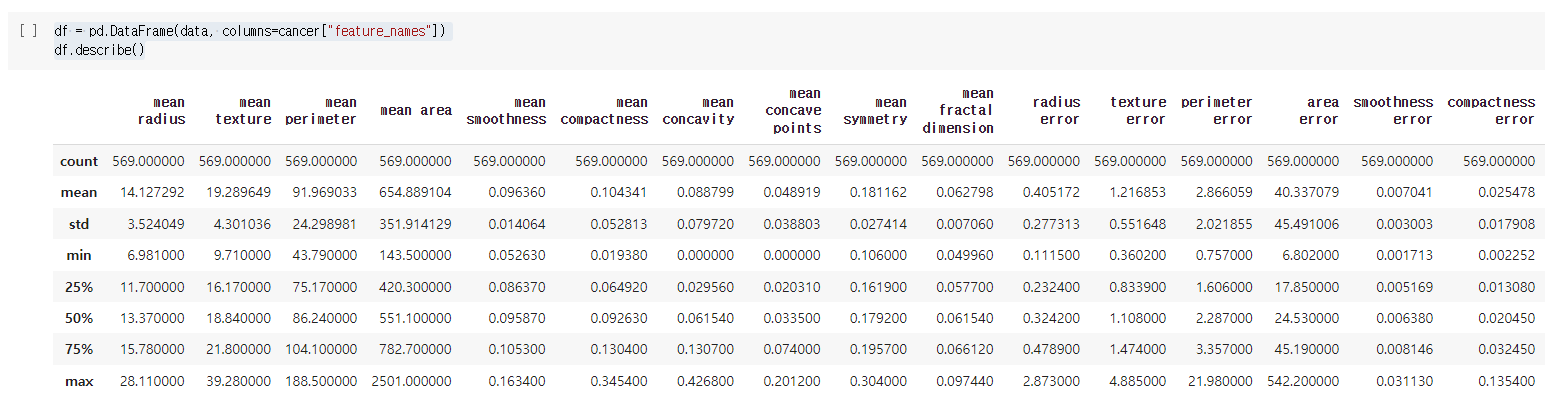
df = pd.DataFrame(data, columns=cancer["feature_names"])
df.describe()위 코드는 유방암 데이터셋에서 가져온 feature 데이터를 이용하여 pandas DataFrame을 생성하고, describe() 함수를 사용하여 데이터셋의 통계 정보를 출력합니다.
pd.DataFrame(data, columns=cancer["feature_names"]): 유방암 데이터셋에서 가져온 feature 데이터를 이용하여 pandas DataFrame을 생성합니다. 이 때, columns 매개변수를 이용하여 각 feature 데이터의 이름을 지정합니다.
df.describe(): 생성된 DataFrame의 통계 정보를 출력합니다. count, mean, std, min, 25%, 50%, 75%, max 순으로, 각 feature에 대한 통계 정보가 출력됩니다.
따라서 위 코드의 결과는 DataFrame의 각 feature 데이터에 대한 통계 정보가 출력됩니다. 예를 들어, mean 값은 각 feature의 데이터 평균값을, std 값은 각 feature의 데이터 표준편차를 나타냅니다.
대충 아래와 같이 출력된다..!
data.shapedata.shape: 유방암 데이터셋에서 가져온 feature 데이터의 shape 정보를 출력합니다. 이 때, shape 정보는 (샘플 수, feature 수) 형태로 출력됩니다.
따라서 위 코드의 결과는 (샘플 수, feature 수) 형태의 데이터 shape 정보가 출력됩니다. 예를 들어, (569, 30)은 569개의 샘플이 있으며, 각 샘플은 30개의 feature 데이터로 이루어져 있다는 것을 나타냅니다.
양성과 음성의 비율은 다음과 같습니다.
pd.Series(target).value_counts()
Histogram으로 그리면 다음과 같습니다.
plt.hist(target)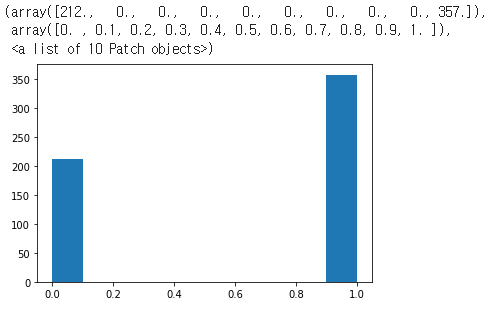
mean radius와 정답간의 상관관계를 plot으로 그리면 다음과 같습니다.
mean radius가 클 경우 음성인 것을 확인할 수 있습니다.
plt.scatter(x=data[:,0], y=target)
plt.xlabel("mean radius")
plt.ylabel("target")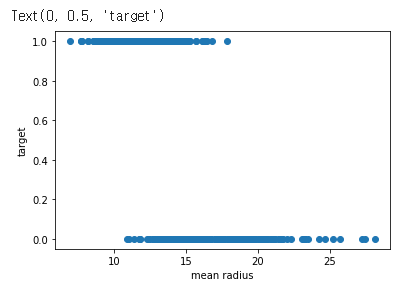
즉,
위 코드는 유방암 데이터셋에서 가져온 target 데이터를 이용하여 pandas Series 객체를 생성하고, 이를 바탕으로 value_counts() 함수를 사용하여 각 클래스별 데이터 개수를 출력합니다.
이어서, matplotlib의 hist() 함수와 scatter() 함수를 이용하여 각각 히스토그램과 산점도를 그립니다.
- pd.Series(target).value_counts(): 유방암 데이터셋에서 가져온 target 데이터를 이용하여 pandas Series 객체를 생성합니다. 이 객체에 대해서 value_counts() 함수를 사용하여 각 클래스별 데이터 개수를 출력합니다.
- plt.hist(target): target 데이터에 대한 히스토그램을 그립니다. 이 때, 히스토그램은 각 클래스별 데이터 개수를 표시합니다.
- plt.scatter(x=data[:,0], y=target): 유방암 데이터셋에서 가져온 feature 데이터 중 첫 번째 feature와 target 데이터 간의 관계를 산점도로 나타냅니다. 이 때, x축에는 첫 번째 feature 데이터를, y축에는 target 데이터를 사용합니다.
- plt.xlabel("mean radius"): x축의 라벨을 "mean radius"로 설정합니다.
- plt.ylabel("target"): y축의 라벨을 "target"으로 설정합니다.
따라서 위 코드의 결과는 유방암 데이터셋에서 가져온 target 데이터에 대한 각 클래스별 데이터 개수, target 데이터에 대한 히스토그램, 유방암 데이터셋에서 가져온 feature 데이터 중 첫 번째 feature와 target 데이터 간의 관계를 나타낸 산점도가 출력됩니다.
Data Split
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
np.random.seed(2021)
cancer = load_breast_cancer()
data, target = cancer["data"], cancer["target"]
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021,
)
print("train data 개수:", len(train_data))
print("test data 개수:", len(test_data))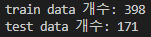
위 코드는 scikit-learn의 load_breast_cancer 함수를 이용하여 유방암 데이터를 로드하고, train_test_split 함수를 이용하여 이를 학습 데이터와 검증 데이터로 나누는 코드입니다.
먼저, np.random.seed(2021) 코드는 랜덤 시드를 고정하는 코드입니다. 이를 통해 코드를 실행할 때마다 동일한 결과를 얻을 수 있습니다.
그 다음, load_breast_cancer 함수를 이용하여 유방암 데이터를 불러와서 data와 target 변수에 저장합니다. 이 때, data 변수는 569개의 샘플과 30개의 특성을 가진 2차원 배열이고, target 변수는 각 샘플의 클래스 정보를 가진 1차원 배열입니다.
마지막으로, train_test_split 함수를 이용하여 data와 target을 학습 데이터와 검증 데이터로 나누고, 이를 각각 train_data, test_data, train_target, test_target 변수에 저장합니다. 이 때, train_size 인자를 이용하여 학습 데이터의 비율을 설정하고, random_state 인자를 이용하여 랜덤 시드를 고정합니다. 마지막으로, print 함수를 이용하여 학습 데이터와 검증 데이터의 개수를 출력합니다.
따라서, 위 코드는 유방암 데이터를 학습 데이터와 검증 데이터로 나누고, 이에 대한 개수를 출력하는 코드입니다.
Linear Regression and Categorical Label
Logistic Regression을 학습하기에 앞서 Linear Regression으로 학습할 경우 어떻게 되는지 확인해 보겠습니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
linear_regressor = LinearRegression() #학습
train_pred = linear_regressor.predict(train_data) #예측
test_pred = linear_regressor.predict(test_data)
train_pred[:10]위 코드는 Scikit-learn의 선형 회귀 모델(Linear Regression)을 이용하여 학습 데이터와 검증 데이터에 대한 예측값을 구하는 코드입니다.
먼저, LinearRegression 클래스의 인스턴스를 생성하고 linear_regressor 변수에 저장합니다. 그 다음, 생성한 linear_regressor를 이용하여 train_data에 대한 예측값을 train_pred 변수에 저장하고, test_data에 대한 예측값을 test_pred 변수에 저장합니다.
마지막으로, train_pred 변수의 첫 10개 값을 출력하는 코드입니다. train_pred는 train_data에 대한 예측값을 저장한 변수이므로, 이를 출력하면 학습 데이터에 대한 첫 10개 샘플의 예측값을 볼 수 있습니다.
하지만, 위 코드에서는 train_data와 test_data를 이용하여 예측값을 구하였지만, Linear Regression 모델의 경우 학습을 진행한 후 예측을 해야 정확한 결과를 얻을 수 있습니다. 따라서 위 코드는 학습이 진행되지 않은 상태에서 예측값을 구하였기 때문에 실제 결과와는 다를 수 있습니다. 즉, 예측한 결과를 보면 0~1사이를 벗어난 예측값을 많이 볼 수 있습니다.
즉, 전체 코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_breast_cancer
np.random.seed(2021)
cancer = load_breast_cancer()
data, target = cancer["data"], cancer["target"]
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021,
)
linear_regressor = LinearRegression()
linear_regressor.fit(train_data, train_target)
train_pred = linear_regressor.predict(train_data)
test_pred = linear_regressor.predict(test_data)
print(train_pred[:10])이 코드는 scikit-learn에서 제공하는 load_breast_cancer() 함수를 사용하여 유방암 데이터셋을 로드하고, 이를 훈련 데이터셋과 테스트 데이터셋으로 분할한 다음, 선형 회귀 모델을 훈련시키고 예측을 수행합니다.
load_breast_cancer() 함수를 사용하여 유방암 데이터셋을 로드합니다.
데이터셋의 feature matrix를 data 변수에 할당하고, target vector를 target 변수에 할당합니다.
train_test_split() 함수를 사용하여 데이터를 훈련용과 테스트용으로 분할합니다. 이때 훈련용 데이터셋의 크기를 전체 데이터의 70%로 지정하고, 난수 발생기의 시드값을 2021로 설정합니다.
LinearRegression() 함수를 사용하여 선형 회귀 모델을 만듭니다.
fit() 메소드를 사용하여 선형 회귀 모델을 훈련시킵니다.
predict() 메소드를 사용하여 훈련 데이터셋과 테스트 데이터셋에 대한 예측값을 계산합니다.
print() 함수를 사용하여 훈련 데이터셋에서 처음 10개의 예측값을 출력합니다.
위 출력 결과는 훈련 데이터셋에서 예측한 첫 10개 데이터의 예측값입니다. 각 예측값은 실수값으로 나타나며, 회귀 모델이 예측한 해당 데이터 샘플의 타겟 변수 값을 추정한 것입니다.
시각화
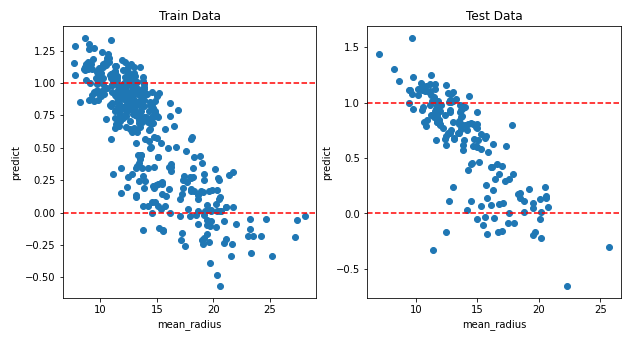
mean_radius의 값에 변화에 따른 예측한 결과를 시각화하면 다음과 같습니다.
전체적으로 우하향하는 예측을 하는 것을 알 수 있습니다.
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
preds = [
("Train", train_data, train_pred),
("Test", test_data, test_pred),
]
for idx, (name, d, pred) in enumerate(preds):
ax = axes[idx]
ax.scatter(x=d[:,0], y=pred)
ax.axhline(0, color="red", linestyle="--")
ax.axhline(1, color="red", linestyle="--")
ax.set_xlabel("mean_radius")
ax.set_ylabel("predict")
ax.set_title(f"{name} Data")해당 코드는 앞서 구한 train_data, train_pred, test_data, test_pred를 이용하여 산점도를 그리는 코드입니다.
preds는 ("Train", train_data, train_pred)와 ("Test", test_data, test_pred) 두 개의 튜플을 원소로 갖는 리스트입니다. 각각의 튜플은 이름, 데이터, 예측값으로 이루어져 있습니다.
for 루프에서는 preds 리스트를 반복하면서 idx와 (name, d, pred) 변수를 언패킹합니다. idx는 0부터 1까지 반복하며, (name, d, pred)는 preds 리스트의 각 튜플의 원소를 가리킵니다.
ax는 idx번째 서브플롯입니다. scatter 함수를 이용하여 d[:,0]과 pred를 산점도로 그립니다. axhline 함수를 이용하여 y축이 0과 1일 때의 가로선을 그리고, set_xlabel, set_ylabel, set_title 함수를 이용하여 x축, y축, 타이틀을 설정합니다.
마지막으로 plt.show() 함수를 이용하여 그래프를 출력합니다.
평가하기
Linear Regression의 성능을 측정하기 위해서는 우선 예측값을 0과 1로 변환시켜줘야 합니다.
강의에서 배웠던 Youden's Index를 이용해 Best Threshold를 찾은 후 0과 1로 변화시킨 후 정확도를 보겠습니다.
from sklearn.metrics import auc, roc_curve
fpr, tpr, threshold = roc_curve(train_target, train_pred)
auroc = auc(fpr, tpr)
fpr
tpr
threshold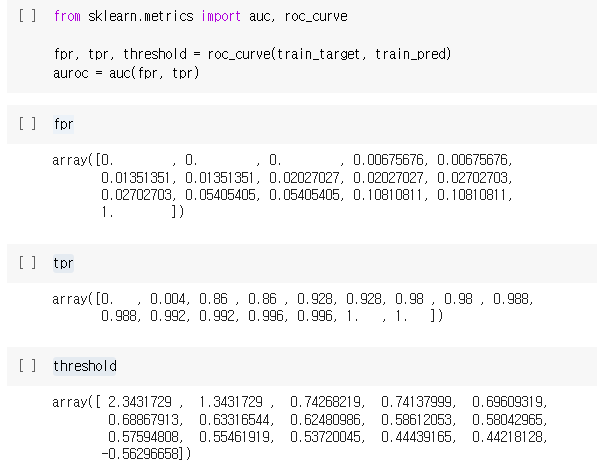
위 코드는 train_data와 train_target을 사용하여 선형회귀 모델을 학습한 후, 학습 데이터에 대해 예측 값을 계산하고 이를 바탕으로 ROC 곡선을 그리기 위해 필요한 FPR, TPR 및 임계값(threshold)을 계산한 것입니다.
roc_curve() 함수는 실제 값(train_target)과 예측 값(train_pred)을 입력으로 받아 FPR, TPR 및 임계값(threshold)을 계산합니다.
auc() 함수는 FPR 및 TPR 값의 쌍을 입력으로 받아 ROC 곡선 아래 면적(Area Under the Curve)을 계산합니다.
따라서, fpr은 FPR 값의 배열, tpr은 TPR 값의 배열, threshold는 계산된 임계값(threshold)의 배열을 각각 저장하고 있습니다.
즉, 이 코드는 유방암 데이터셋을 사용하여 Linear Regression 모델을 학습하고, 학습된 모델로부터 train data와 test data에 대한 예측값을 구한 뒤, train data에 대한 ROC Curve와 AUC 값을 계산하는 코드입니다.
코드의 구체적인 작동 방식은 다음과 같습니다.
필요한 패키지와 모듈을 import합니다.
유방암 데이터셋을 로드합니다.
데이터셋에서 입력 데이터와 목표 변수를 추출합니다.
입력 데이터와 목표 변수를 train set과 test set으로 분리합니다.
Linear Regression 모델을 초기화합니다.
train set을 사용하여 Linear Regression 모델을 학습시킵니다.
train set과 test set에 대해 모델을 사용하여 예측값을 구합니다.
train set에 대한 ROC Curve와 AUC 값을 계산합니다.
이 때, ROC Curve와 AUC 값은 모델의 분류 성능을 평가하는 데 사용되는 지표입니다. ROC Curve는 FPR(False Positive Rate)과 TPR(True Positive Rate)의 변화에 따른 그래프를 나타내며, AUC는 ROC Curve 아래 면적을 의미합니다. 이 값이 1에 가까울수록 모델의 분류 성능이 좋다고 판단할 수 있습니다.
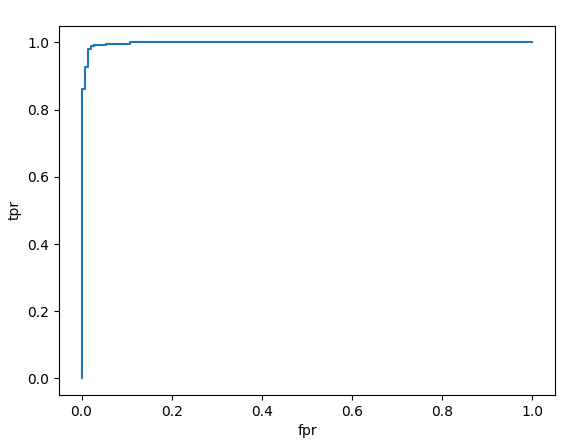
우선 AUROC 를 그려보겠습니다.
plt.plot(fpr, tpr)
plt.xlabel("fpr")
plt.ylabel("tpr")위 코드는 ROC 곡선을 그리기 위해 fpr(False Positive Rate)을 x축으로, tpr(True Positive Rate)을 y축으로 하는 2차원 좌표계상에 (fpr, tpr) 점들을 연결한 곡선을 그리는 코드입니다. ROC 곡선은 분류 모델의 성능을 판단할 때 많이 사용되는 평가지표 중 하나로, 분류 임계값을 다양하게 조정했을 때 분류 모델의 민감도와 특이도가 어떻게 변하는지를 나타내는 곡선입니다. 분류 모델의 성능이 우수할수록 ROC 곡선은 좌측 상단에 가까운 곡선이 그려집니다.
AUROC 값을 계산하면 다음과 같습니다.
print(f"AUROC : {auroc:.4f}")위 코드는 계산한 AUROC 값을 소수점 넷째 자리까지 출력해주는 코드입니다. auroc 변수에 계산한 AUROC 값을 저장하고, f-string을 이용하여 출력합니다. 소수점 이하 넷째 자리까지 출력하기 위해 .4f를 사용합니다.

이제 Best Threshold를 계산해 보겠습니다.
np.argmax(tpr - fpr)J = tpr - fpr
idx = np.argmax(J)
best_thresh = threshold[idx]
print(f"Best Threshold is {best_thresh:.4f}")
print(f"Best Threshold's sensitivity is {tpr[idx]:.4f}")
print(f"Best Threshold's specificity is {1-fpr[idx]:.4f}")
print(f"Best Threshold's J is {J[idx]:.4f}")이 코드는 위에서 구한 fpr, tpr, threshold를 이용해서 최적의 분류 기준값(threshold)을 찾아내고, 그 때의 sensitivity, specificity, J 값을 출력하는 코드입니다.
np.argmax 함수는 배열에서 가장 큰 값을 갖는 인덱스를 반환합니다. tpr-fpr의 값을 최대로 하는 인덱스를 구해서 최적의 분류 기준값을 찾아냅니다. 그리고 그 때의 sensitivity, specificity, J 값을 구해서 출력합니다.
sensitivity: 진양성비율, TP / (TP + FN)
specificity: 진음성비율, TN / (FP + TN)
J : Youden's index, sensitivity + specificity - 1
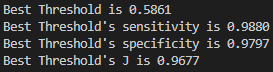
Best Threshold는 AUROC 그래프에서 직선이 가장 긴 곳입니다.
한번 Plot을 직접 그려보겠습니다.
plt.plot(fpr, tpr)
plt.plot(np.linspace(0, 1, 10), np.linspace(0, 1, 10))
plt.plot((fpr[idx], fpr[idx]), (fpr[idx], tpr[idx]), color="red", linestyle="--")
plt.xlabel("fpr")
plt.ylabel("tpr")이 코드는 이진 분류 모델의 ROC 곡선을 나타내는 그래프를 생성합니다. 첫 번째 줄은 x축에 false positive rate(fpr)를, y축에 true positive rate(tpr)를 사용하여 ROC 곡선을 그립니다. 두 번째 줄은 무작위 분류기의 ROC 곡선을 나타내기 위해 왼쪽 하단 모서리에서 오른쪽 상단 모서리로 대각선 라인을 추가합니다. 세 번째 줄은 J 통계량을 최대화하는 임계값의 인덱스인 idx를 사용하여 (fpr[idx], fpr[idx])에서 (fpr[idx], tpr[idx])로 빨간 점선을 추가합니다. 이 라인은 선택된 임계값에서 ROC 곡선 상의 동작 점을 보여줍니다. 마지막으로 마지막 두 줄은 그래프의 x축과 y축에 레이블을 추가합니다.
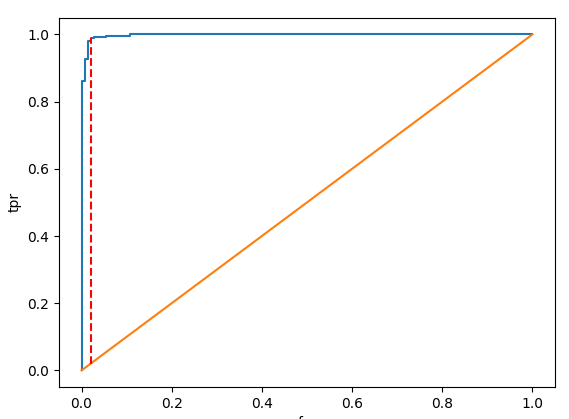
예측값에서의 Best threshold의 위치를 그려보겠습니다.
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
preds = [
("Train", train_data, train_pred),
("Test", test_data, test_pred),
]
for idx, (name, d, pred) in enumerate(preds):
ax = axes[idx]
ax.scatter(x=d[:,0], y=pred)
ax.axhline(0, color="red", linestyle="--")
ax.axhline(1, color="red", linestyle="--")
ax.set_xlabel("mean_radius")
ax.set_ylabel("predict")
ax.set_title(f"{name} Data")
ax.axhline(best_thresh, color="blue")이 코드는 두 개의 subplot을 가지는 그래프를 생성합니다. 각 subplot은 특성 mean_radius와 예측값 사이의 산점도를 보여줍니다. 'Train'과 'Test' 두 가지 데이터 세트에 대한 subplot이 있으며, 각 subplot에는 예측값이 0 또는 1인 경우를 나타내는 빨간 점선이 포함되어 있습니다. 또한, 최적 임계값인 best_thresh에 해당하는 파란색 점선도 subplot에 추가됩니다. 마지막으로, 각 subplot에 x축과 y축에 레이블이 추가됩니다.
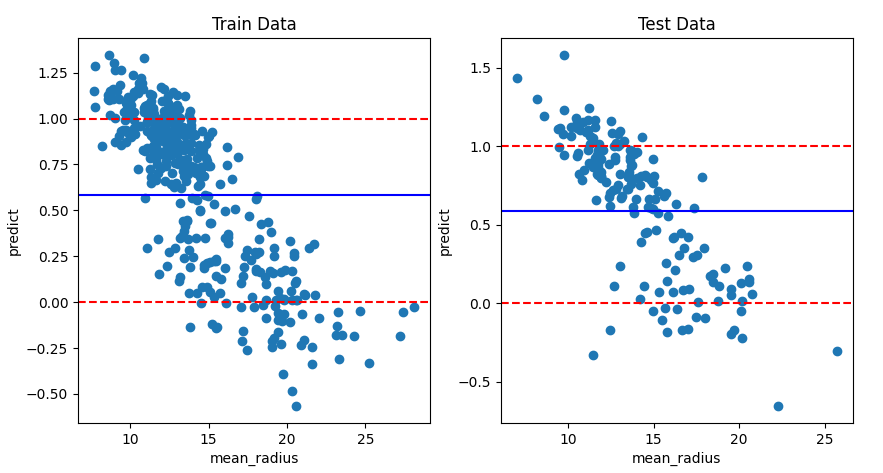
이제 Threshold로 예측값을 0,1로 변환 후 정확도를 보겠습니다.
train_pred_label = list(map(int, (train_pred > best_thresh)))
test_pred_label = list(map(int, (test_pred > best_thresh)))
from sklearn.metrics import accuracy_score
linear_train_accuracy = accuracy_score(train_target, train_pred_label)
linear_test_accuracy = accuracy_score(test_target, test_pred_label)
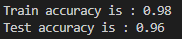
print(f"Train accuracy is : {linear_train_accuracy:.2f}")
print(f"Test accuracy is : {linear_test_accuracy:.2f}")이 코드는 이진 분류 모델의 예측 결과를 이용하여 Train set과 Test set의 정확도를 계산하는 코드입니다.
train_pred_label과 test_pred_label은 각각 train_pred와 test_pred에서 best_thresh를 기준으로 이진 분류한 결과로, map 함수를 이용하여 0 또는 1로 변환된 리스트입니다.
그 다음, scikit-learn의 accuracy_score 함수를 이용하여 Train set과 Test set에서의 예측 정확도를 구하고 출력합니다.
Logistic Regression
- Scaling
Logistic Regression은 학습하기에 앞서 학습시킬 데이터를 정규화해야 합니다.
Logistic Regressiond에는 exp가 있는데, exp는 값이 클 경우 overflow가 일어날 수 있기 때문입니다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()scaler.fit(train_data)- 학습된 scaler로 train/ test 데이터를 변환합니다.
scaled_train_data = scaler.transform(train_data)
scaled_test_data = scaler.transform(test_data)train_data[0]scaled_train_data[0]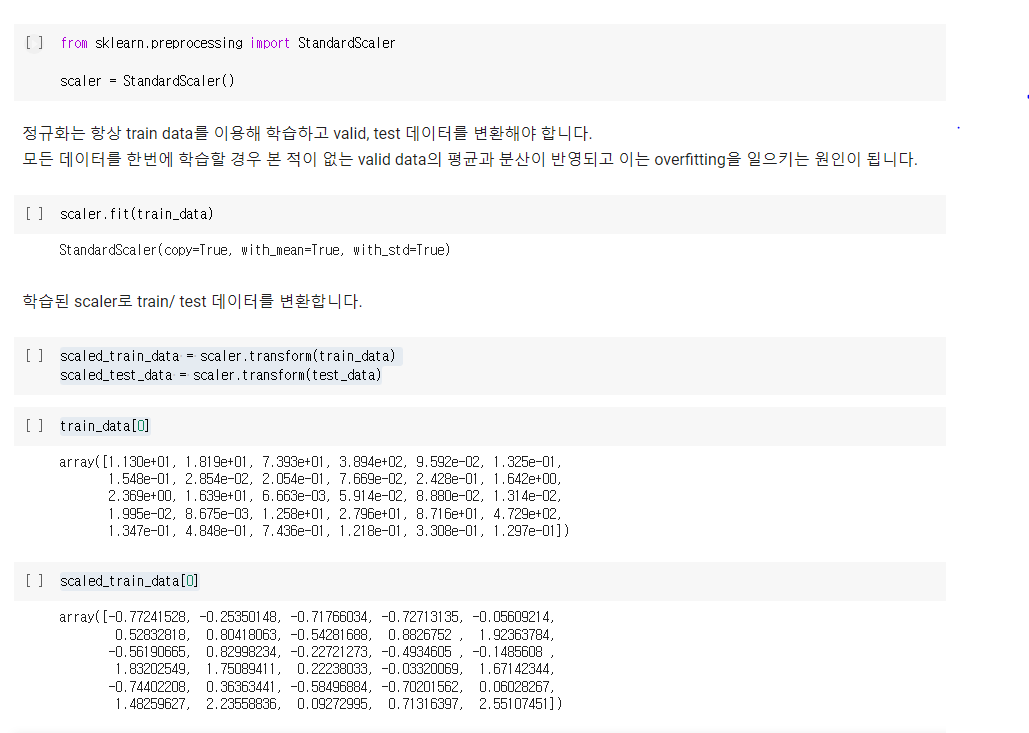
로지스틱 회귀(Logistic Regression)는 입력 데이터의 값의 범위에 따라 모델의 예측 결과에 영향을 받을 수 있습니다. 예를 들어, 입력 데이터의 값의 범위가 크고 작은 경우, 해당 입력 데이터가 예측 결과에 미치는 영향이 다르게 됩니다.
따라서, 로지스틱 회귀에서는 입력 데이터의 값의 범위를 정규화(normalization)하여, 입력 데이터의 값이 모두 비슷한 범위에 있도록 해주는 것이 일반적입니다. 이를 위해, StandardScaler를 사용하여 입력 데이터를 평균이 0, 표준편차가 1인 범위로 변환합니다.
위 코드에서, scaler.fit(train_data)를 사용하여 scaler 객체를 학습시키고, scaled_train_data = scaler.transform(train_data)를 사용하여 학습된 scaler로 train 데이터를 변환합니다. 이후 train_data[0]과 scaled_train_data[0]를 출력하여 원래 데이터와 정규화된 데이터의 값의 차이를 확인할 수 있습니다.
학습 - 이제 표준화된 데이터로 Logistic Regression을 학습해 보겠습니다.
from sklearn.linear_model import LogisticRegression
logit_regressor = LogisticRegression()
logit_regressor.fit(scaled_train_data, train_target)예측 - Classification 을 하는 모델의 경우 예측을 하는 방법은 두 가지가 있습니다.
- predict
- predict_proba
predict는 해당 데이터가 어떤 class로 분류할지 바로 알려줍니다.
반면, predict_proba는 각 class에 속할 확률을 보여줍니다.
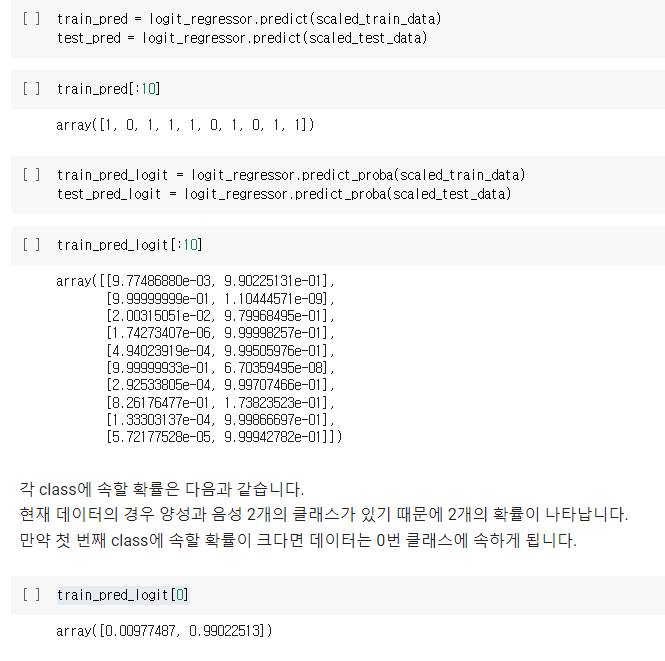
train_pred = logit_regressor.predict(scaled_train_data)
test_pred = logit_regressor.predict(scaled_test_data)
train_pred[:10]
train_pred_logit = logit_regressor.predict_proba(scaled_train_data)
test_pred_logit = logit_regressor.predict_proba(scaled_test_data)
train_pred_logit[:10]각 class에 속할 확률은 다음과 같습니다.
현재 데이터의 경우 양성과 음성 2개의 클래스가 있기 때문에 2개의 확률이 나타납니다.
만약 첫 번째 class에 속할 확률이 크다면 데이터는 0번 클래스에 속하게 됩니다.
train_pred_logit[0]해당 코드는 로지스틱 회귀 모델의 predict_proba() 메서드를 이용하여 학습 데이터의 첫 번째 샘플이 양성 클래스(1)와 음성 클래스(0)에 속할 확률을 보여주는 것입니다. 즉, train_pred_logit[0]은 첫 번째 샘플이 음성 클래스에 속할 확률과 양성 클래스에 속할 확률을 보여주는 배열입니다. 이 배열의 첫 번째 원소는 음성 클래스에 속할 확률을, 두 번째 원소는 양성 클래스에 속할 확률을 나타냅니다.
즉, 지금까지 전체 코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import auc, roc_curve
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
np.random.seed(2021)
cancer = load_breast_cancer()
data, target = cancer["data"], cancer["target"]
train_data, test_data, train_target, test_target = train_test_split(
data, target, train_size=0.7, random_state=2021,
)
linear_regressor = LinearRegression()
linear_regressor.fit(train_data, train_target)
train_pred = linear_regressor.predict(train_data)
test_pred = linear_regressor.predict(test_data)
fpr, tpr, threshold = roc_curve(train_target, train_pred)
auroc = auc(fpr, tpr)
scaler = StandardScaler()
scaled_train_data = scaler.fit_transform(train_data)
scaled_test_data = scaler.transform(test_data)
print(train_data[0])
print(scaled_train_data[0])
logit_regressor = LogisticRegression()
logit_regressor.fit(scaled_train_data, train_target)
train_pred = logit_regressor.predict(scaled_train_data)
test_pred = logit_regressor.predict(scaled_test_data)
train_pred[:10]
train_pred_logit = logit_regressor.predict_proba(scaled_train_data)
test_pred_logit = logit_regressor.predict_proba(scaled_test_data)
train_pred_logit[:10]
train_pred_logit[0]평가
데이터의 AUROC를 계산하기 위해서는 1의 클래스로 분류될 확률 하나만 필요합니다.
반면 우리가 갖고 있는 예측값은 0과 1로 분류될 확률을 모두 표시하고 있습니다.
그래서 1에 속할 확률만 남기겠습니다.
train_pred_logit = train_pred_logit[:, 1]
test_pred_logit = test_pred_logit[:, 1]
train_pred_logit[0]
from sklearn.metrics import auc, roc_curve
fpr, tpr, threshold = roc_curve(train_target, train_pred_logit)
auroc = auc(fpr, tpr)
plt.plot(fpr, tpr)
plt.xlabel("fpr")
plt.ylabel("tpr")위 코드는 ROC 곡선을 그리기 위한 코드입니다.
우선 train_pred_logit와 test_pred_logit에서 두 번째 열을 선택하여 train_pred_logit와 test_pred_logit를 각각 덮어씌웁니다. 이는 predict_proba에서 반환된 값이 첫 번째 열은 음성 클래스에 속할 확률, 두 번째 열은 양성 클래스에 속할 확률을 나타내는데, 여기서는 양성 클래스에 속할 확률만 필요하기 때문입니다.
그 다음으로는 sklearn.metrics 모듈에서 제공하는 roc_curve 함수를 사용하여 train_target와 train_pred_logit를 입력으로 받아 False Positive Rate(FPR), True Positive Rate(TPR), 그리고 Threshold 값을 반환합니다. 반환된 값들을 이용하여 ROC 곡선을 그립니다.
마지막으로 xlabel과 ylabel을 사용하여 x축과 y축에 이름을 붙이고, 이를 plt 모듈에서 제공하는 plot 함수를 이용하여 시각화합니다.
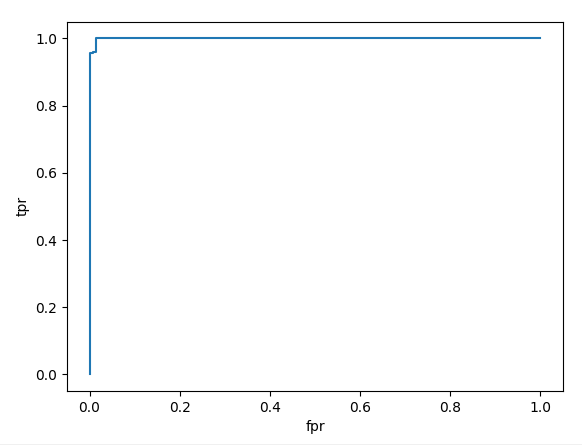
print(f"AUROC : {auroc:.4f}") #AUROC : 0.9994
J = tpr - fpr
idx = np.argmax(J)
best_thresh = threshold[idx]
print(f"Best Threshold is {best_thresh:.4f}")
print(f"Best Threshold's sensitivity is {tpr[idx]:.4f}")
print(f"Best Threshold's specificity is {1-fpr[idx]:.4f}")
print(f"Best Threshold's J is {J[idx]:.4f}")
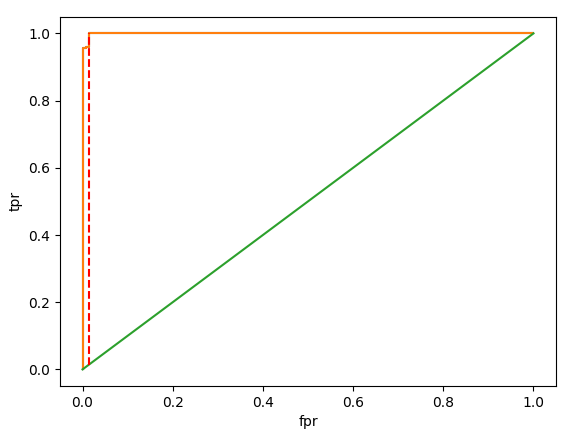
plt.plot(fpr, tpr)
plt.plot(np.linspace(0, 1, 10), np.linspace(0, 1, 10))
plt.plot((fpr[idx],fpr[idx]), (fpr[idx], tpr[idx]), color="red", linestyle="--")
plt.xlabel("fpr")
plt.ylabel("tpr")
plt.show()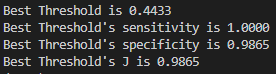
위 코드는 로지스틱 회귀 모델의 분류 성능을 평가하고, 최적의 분류 임계값(threshold)과 해당 임계값에서의 성능 지표를 출력하는 코드입니다.
train_pred_logit과 test_pred_logit에 저장된 각 샘플이 양성 클래스(악성 종양)에 속할 확률을 기반으로, 학습 데이터에서 임계값에 따라 분류를 수행합니다.
ROC 곡선을 그리기 위해 sklearn.metrics 모듈의 roc_curve 함수를 이용하여 FPR(False Positive Rate)과 TPR(True Positive Rate)를 계산합니다. 이를 기반으로 AUC(Area Under the ROC Curve) 값을 계산하여 AUROC 지표를 출력합니다.
또한, 임계값을 변화시키면서 FPR과 TPR의 변화를 관찰하고, FPR=TNR와 TPR=Sensitivity의 지점을 기준으로 최적의 분류 임계값을 결정합니다. 최적의 분류 임계값에서의 성능 지표(J)를 계산하여 출력하고, 이를 그래프 상에 표시합니다.
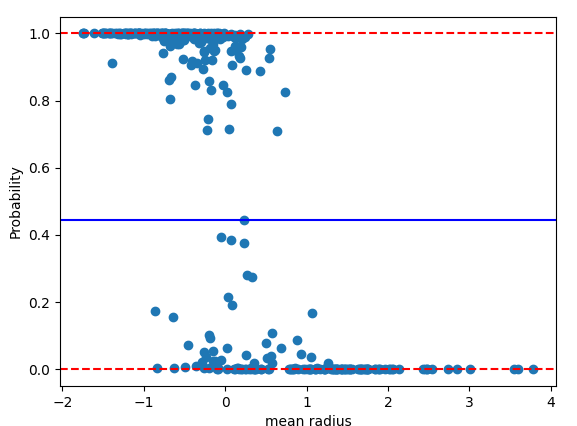
plt.scatter(x=scaled_train_data[:,0], y=train_pred_logit)
plt.axhline(best_thresh, color="blue")
plt.axhline(0, color="red", linestyle="--")
plt.axhline(1, color="red", linestyle="--")
plt.xlabel("mean radius")
plt.ylabel("Probability")
plt.show()
해당 코드는 로지스틱 회귀 모델의 예측 확률과 train 데이터의 첫 번째 feature인 mean radius를 산점도로 그려주는 코드입니다. 로지스틱 회귀 모델에서 0.5를 기준으로 확률이 큰 쪽에 해당 데이터를 분류합니다. 그래서 plt.axhline(best_thresh, color="blue") 코드는 모델에서 계산된 최적의 임계값을 그래프에 파란색 점선으로 표시하는 것입니다. 또한, plt.axhline(0, color="red", linestyle="--")과 plt.axhline(1, color="red", linestyle="--") 코드는 각각 y축의 0과 1 위치에 빨간색 점선으로 표시합니다. 이는 확률이 0 또는 1인 경우가 최종적으로 어떤 클래스로 분류되더라도 그것이 모델의 결정에 큰 영향을 미치지 않도록 하기 위함입니다. plt.xlabel("mean radius")과 plt.ylabel("Probability") 코드는 x축과 y축에 라벨을 추가해주는 것입니다.
이제 Threshold로 예측값을 0,1로 변환 후 정확도를 보겠습니다.
from sklearn.metrics import accuracy_score
train_pred_label = list(map(int, (train_pred_logit > best_thresh)))
test_pred_label = list(map(int, (test_pred_logit > best_thresh)))
proba_train_accuracy = accuracy_score(train_target, train_pred_label)
proba_test_accuracy = accuracy_score(test_target, test_pred_label)
print(f"Train accuracy is : {proba_train_accuracy:.2f}")
print(f"Test accuracy is : {proba_test_accuracy:.2f}")위 코드는 Logistic Regression 모델의 예측 결과를 활용하여 threshold 값을 구하고, 그 threshold를 기준으로 train 데이터와 test 데이터에 대해 예측 결과를 레이블로 변환하고, 레이블을 기반으로 정확도를 측정하는 코드입니다.
먼저 train_pred_logit과 test_pred_logit에 저장된 예측값에서 양성 클래스(암이 악성인 경우)일 확률에 해당하는 값을 best_thresh를 기준으로 0과 1의 이진 분류 레이블로 변환합니다. 이를 위해 각 데이터에 대해 map 함수와 int 함수를 이용하여 확률값이 best_thresh보다 크면 1, 작으면 0으로 변환합니다.
그리고 accuracy_score 함수를 이용하여 train 데이터와 test 데이터에 대해 예측한 이진 분류 레이블과 실제 레이블을 비교하여 정확도를 계산하고 출력합니다.

이번에는 predict 의 결과값으로 정확도를 보겠습니다.
train_accuracy = accuracy_score(train_target, train_pred)
test_accuracy = accuracy_score(test_target, test_pred)
print(f"Train accuracy is : {train_accuracy:.2f}")
print(f"Test accuracy is : {test_accuracy:.2f}")predict_proba의 best_threshold로 계산한 결과와 predict로 계산한 결과가 다릅니다.
이는 두 0과 1로 예측하는 방법이 다르기 때문입니다.
예를 들어서 (0.49, 0.51)의 확률이 있을 때 predict의 경우 class 1의 확률에 속할 확률이 크기 때문에 1로 분류합니다.
하지만 best_threshold가 0.52라면 predict_proba의 경우 class를 0으로 분류하게 됩니다.

마무리 세개의 모델들의 정확도를 비교해 보겠습니다.
print(f"Linear Regression Test Accuracy: {linear_test_accuracy:.2f}")
print(f"Logistic Regression predict_proba Test Accuracy: {proba_test_accuracy:.2f}")
print(f"Logistic Regression predict Test Accuracy: {test_accuracy:.2f}")이 코드는 선형 회귀 모델과 로지스틱 회귀 모델의 테스트 정확도를 출력합니다. 선형 회귀 모델의 테스트 정확도는 'linear_test_accuracy' 변수에서 계산되며, 로지스틱 회귀 모델의 테스트 정확도는 'proba_test_accuracy' 변수와 'test_accuracy' 변수에서 각각 계산됩니다.
'linear_test_accuracy' 변수는 선형 회귀 모델의 테스트 데이터에 대한 예측값과 실제 타깃값을 비교하여 계산됩니다. 마찬가지로 'proba_test_accuracy' 변수와 'test_accuracy' 변수는 로지스틱 회귀 모델의 예측값과 실제 타깃값을 비교하여 계산됩니다.
이 코드를 통해 선형 회귀 모델과 로지스틱 회귀 모델의 성능을 정확도를 기반으로 평가할 수 있습니다.

