당뇨병 진행도와 관련된 데이터를 이용해 당뇨병 진행을 예측하는 Linear Regression을 학습해 보겠습니다.
Data Load
데이터는 sklearn.datasets 의 load_diabetes 함수를 이용해 받을 수 있습니다.
당뇨병 데이터에서 사용되는 변수명은 feature_names 키 값으로 들어 있습니다.
변수명과 변수에 대한 설명은 다음과 같습니다.
age: 나이
sex: 성별
bmi: Body mass index
bp: Average blood pressure
혈청에 대한 6가지 지표들
S1, S2, S3, S4, S5, S6
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
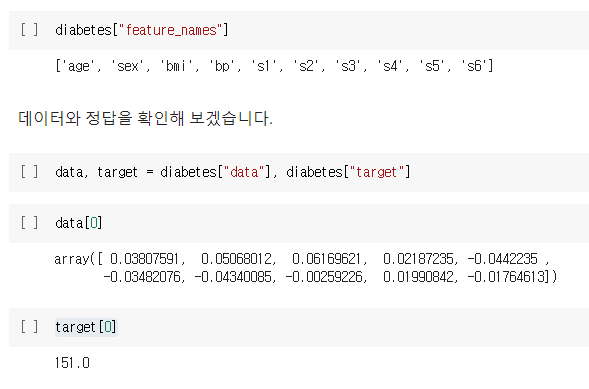
diabetes["feature_names"]
data, target = diabetes["data"], diabetes["target"]
data[0]
target[0] #첫 번째 샘플에 해당하는 당뇨병 진행 상태를 나타내는 값이 코드는 Pandas, NumPy, Matplotlib 및 Scikit-learn 라이브러리를 사용하여 당뇨병 데이터를 로드하고 시각화하는 예제입니다.
np.random.seed(2021): NumPy의 난수 생성기를 초기화하여 실행 시마다 동일한 결과를 생성합니다.
from sklearn.datasets import load_diabetes: Scikit-learn에서 제공하는 당뇨병 데이터를 로드합니다.
diabetes["feature_names"]: 당뇨병 데이터의 특성 이름을 가져옵니다.
data, target = diabetes["data"], diabetes["target"]: 데이터와 타겟을 가져옵니다.
data[0]: 데이터에서 첫 번째 샘플의 값을 가져옵니다.
target[0]: 타겟에서 첫 번째 샘플의 값을 가져옵니다.
즉, 이 코드는 Scikit-learn에서 제공하는 당뇨병 데이터를 NumPy 배열 형태로 가져오고, 이를 Pandas로 변환하여 데이터를 분석 및 시각화하는 데 사용할 수 있습니다.
Data EDA
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
diabetes["feature_names"]
data, target = diabetes["data"], diabetes["target"]
df = pd.DataFrame(data, columns=diabetes["feature_names"])
df.describe()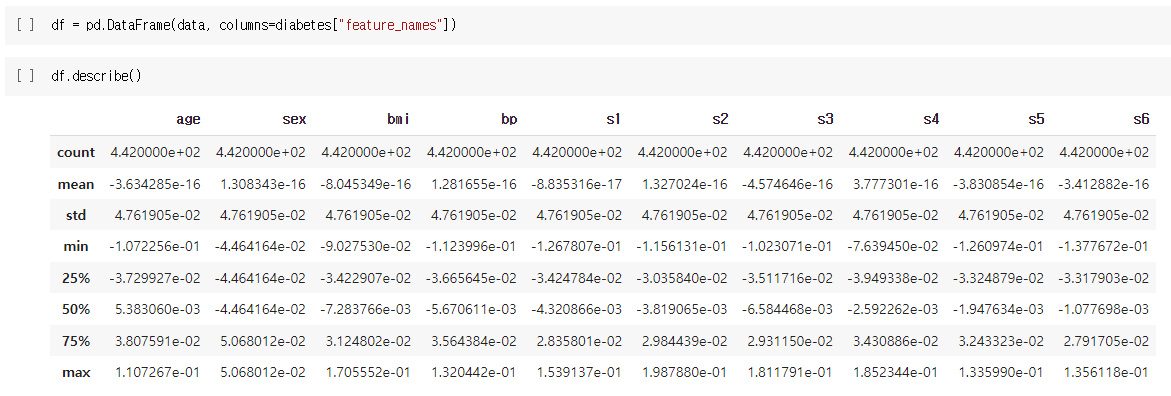
위 코드는 data 배열을 pd.DataFrame으로 변환하고, 이를 당뇨병 데이터의 특성 이름을 컬럼 이름으로 지정하여 데이터를 요약하는 코드입니다.
describe() 함수는 데이터프레임의 주요 통계치를 보여줍니다. 예를 들어, count는 각 열에 있는 비어 있지 않은 값의 수를 보여주고, mean은 열의 평균값, std는 열의 표준편차를 보여줍니다. 이를 통해 데이터의 분포와 중심 경향성 등을 파악할 수 있습니다.
Data Split
sklearn.model_selection의 train_test_split함수를 이용해 데이터를 나누겠습니다.
train_test_split(
*arrays,
test_size=None,
train_size=None,
random_state=None,
shuffle=True,
stratify=None,
)*arrays: 입력은 array로 이루어진 데이터을 받습니다.
test_size: test로 분할될 사이즈를 정합니다.
train_size: train으로 분할될 사이즈를 정합니다.
random_state: 다음에도 같은 값을 얻기 위해서 난수를 고정합니다
shuffle: 데이터를 섞을지 말지 결정합니다.
stratify: 데이터를 나눌 때 정답의 분포를 반영합니다.
sklearn.model_selection의 train_test_split() 함수는 입력된 데이터를 훈련용 데이터와 테스트용 데이터로 분할하는 함수입니다. 분할할 때, 입력된 데이터를 랜덤하게 섞어서 분할하므로, 분할 결과는 매번 달라질 수 있습니다.
*arrays는 입력된 데이터 배열을 의미합니다. 이 함수는 이를 훈련 데이터와 테스트 데이터로 분할합니다. test_size는 테스트 데이터로 사용할 비율을 지정합니다. 예를 들어, test_size=0.2이면, 전체 데이터 중 20%를 테스트 데이터로 사용하고 나머지 80%를 훈련 데이터로 사용합니다. train_size는 훈련 데이터로 사용할 비율을 지정할 수도 있습니다. test_size와 train_size 중 하나를 반드시 지정해야 하며, 둘 다 지정하지 않으면, test_size는 0.25, train_size는 0.75로 설정됩니다.
random_state는 난수 발생 시드(seed) 값을 지정합니다. 이 값이 동일하면, 항상 같은 결과를 반환합니다. shuffle은 데이터를 분할하기 전에 섞을 것인지 지정합니다. stratify는 클래스 분포를 고려하여 데이터를 나눌 때 사용합니다. 이를 지정하면, 각 클래스의 비율이 유지되도록 데이터를 나눕니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
np.random.seed(2021)
diabetes = load_diabetes()
data, target = diabetes["data"], diabetes["target"]
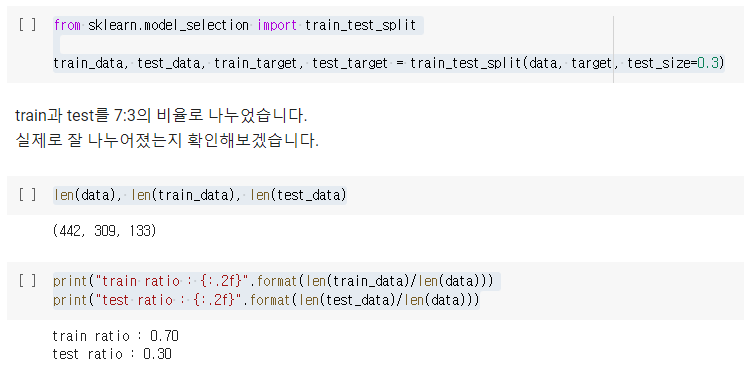
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3) #train과 test를 7:3의 비율로 나누었습니다.
len(data), len(train_data), len(test_data) #실제로 잘 나누어졌는지 확인
print("train ratio : {:.2f}".format(len(train_data)/len(data)))
print("test ratio : {:.2f}".format(len(test_data)/len(data)))위 코드는 sklearn.model_selection의 train_test_split() 함수를 사용하여 데이터를 훈련용 데이터와 테스트용 데이터로 분할하는 코드입니다.
train_test_split() 함수는 data와 target 배열을 입력으로 받습니다. 이 함수는 이를 훈련용 데이터와 테스트용 데이터로 분할하는데, test_size를 0.3으로 지정하여 전체 데이터 중 30%를 테스트용 데이터로 사용하고 나머지 70%를 훈련용 데이터로 사용합니다.
train_data, test_data, train_target, test_target는 각각 훈련용 데이터, 테스트용 데이터, 훈련용 데이터의 타겟 값, 테스트용 데이터의 타겟 값이 됩니다.
len() 함수를 사용하여 각 데이터의 길이를 출력합니다. 이 코드에서는 전체 데이터의 길이와 훈련용 데이터, 테스트용 데이터의 길이를 출력합니다.
마지막으로, 전체 데이터 대비 훈련용 데이터와 테스트용 데이터의 비율을 출력합니다. 이를 통해, 전체 데이터 중 어느 정도의 비율을 각각의 데이터로 사용하는지 알 수 있습니다.
Multivariate Regression 학습
from sklearn.linear_model import LinearRegression
multi_regressor = LinearRegression()
multi_regressor.fit(train_data, train_target)회귀식 확인
multi_regressor.intercept_
multi_regressor.coef_예측
multi_train_pred = multi_regressor.predict(train_data)
multi_test_pred = multi_regressor.predict(test_data)위 코드는 sklearn.linear_model의 LinearRegression()을 이용하여 다중선형회귀 모델을 학습하는 코드입니다.
LinearRegression()은 다중선형회귀 모델 객체를 생성합니다. 이후 fit() 함수를 이용하여 학습을 진행합니다. fit() 함수의 인자로는 훈련용 데이터와 훈련용 데이터의 타겟값을 입력합니다.
multiregressor.intercept와 multiregressor.coef는 각각 학습된 다중선형회귀 모델의 절편(intercept)과 계수(coefficient)를 출력합니다.
predict() 함수는 학습된 모델을 이용하여 입력 데이터에 대한 예측값을 출력합니다. multi_train_pred는 훈련용 데이터에 대한 예측값, multi_test_pred는 테스트용 데이터에 대한 예측값을 저장합니다.
평가 - sklearn.metrics 의 mean_squared_error를 이용
mean_squared_error는 두 값의 차이의 제곱의 평균을 계산해줍니다.
from sklearn.metrics import mean_squared_error
multi_train_mse = mean_squared_error(multi_train_pred, train_target)
multi_test_mse = mean_squared_error(multi_test_pred, test_target)
print(f"Multi Regression Train MSE is {multi_train_mse:.4f}")
print(f"Multi Regression Test MSE is {multi_test_mse:.4f}")위 코드는 다중선형회귀 모델을 학습하고, 학습한 모델의 성능을 평가하는 코드입니다.
mean_squared_error() 함수를 사용하여 학습한 모델의 평균제곱오차(MSE)를 계산합니다.
MSE는 예측값과 실제값의 차이를 제곱하여 평균한 값입니다. 모델이 예측한 값과 실제 값이 차이가 크면 MSE가 크게 됩니다.
따라서 MSE가 낮을수록 모델의 예측 성능이 좋다고 판단할 수 있습니다.
아래는 위 코드의 결괏값이다.
train_data shape : (309, 10)
train_target shape : (309,)
multi_regressor.intercept_ : 150.23914503908052
multi_regressor.coef_ : [ -69.33374326 -236.85666792 557.93195794 345.15594684 -585.28321132
295.28601493 69.3949839 167.57353947 683.79276086 74.60208979]
Multi Regression Train MSE is 2809.2699
Multi Regression Test MSE is 2944.6574위 결과를 해석하면 다음과 같습니다.
traindata는 309개의 샘플과 10개의 특성을 가진 행렬입니다.
train_target은 309개의 샘플에 대한 실제 당뇨병 진행률 값입니다.
multi_regressor.intercept는 모델이 예측한 y절편값입니다.
multiregressor.coef는 모델이 예측한 가중치(w)값입니다.
Multi Regression Train MSE는 학습 데이터에 대한 MSE값으로, 2809.2699입니다. 이 값은 학습 데이터에 대한 모델의 성능을 나타냅니다. 학습 데이터에 대한 MSE값이 낮을수록 모델의 예측 성능이 좋다고 판단할 수 있습니다.
Multi Regression Test MSE는 테스트 데이터에 대한 MSE값으로, 2944.6574입니다. 이 값은 테스트 데이터에 대한 모델의 성능을 나타냅니다. 테스트 데이터에 대한 MSE값이 낮을수록 모델이 새로운 데이터에 대해 일반화(generalization)할 수 있다고 판단할 수 있습니다.
전체 코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
np.random.seed(2021)
diabetes = load_diabetes()
data, target = diabetes["data"], diabetes["target"]
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3)
multi_regressor = LinearRegression()
multi_regressor.fit(train_data, train_target)
multi_train_pred = multi_regressor.predict(train_data)
multi_test_pred = multi_regressor.predict(test_data)
print("train_data shape :", train_data.shape)
print("train_target shape :", train_target.shape)
print("multi_regressor.intercept_ :", multi_regressor.intercept_)
print("multi_regressor.coef_ :", multi_regressor.coef_)
from sklearn.metrics import mean_squared_error
multi_train_mse = mean_squared_error(multi_train_pred, train_target)
multi_test_mse = mean_squared_error(multi_test_pred, test_target)
print(f"Multi Regression Train MSE is {multi_train_mse:.4f}")
print(f"Multi Regression Test MSE is {multi_test_mse:.4f}")Ridge Regression 학습
from sklearn.linear_model import Ridge
ridge_regressor = Ridge()
ridge_regressor.fit(train_data, train_target)회귀식 확인
ridge_regressor.intercept_
multi_regressor.coef_
ridge_regressor.coef_예측
ridge_train_pred = ridge_regressor.predict(train_data)
ridge_test_pred = ridge_regressor.predict(test_data)평가
ridge_train_mse = mean_squared_error(ridge_train_pred, train_target)
ridge_test_mse = mean_squared_error(ridge_test_pred, test_target)
print(f"Ridge Regression Train MSE is {ridge_train_mse:.4f}")
print(f"Ridge Regression Test MSE is {ridge_test_mse:.4f}")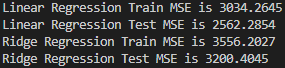
이 코드는 당뇨병 데이터셋을 사용하여 선형 회귀 모델과 릿지 회귀 모델을 학습하고 평가하는 코드입니다.
먼저, Pandas, NumPy, Matplotlib, scikit-learn의 load_diabetes 함수, train_test_split 함수, LinearRegression 클래스, Ridge 클래스, mean_squared_error 함수를 임포트합니다.
다음으로, 난수 생성기의 시드를 설정하고, load_diabetes 함수를 사용하여 데이터와 타겟을 불러옵니다. 그 다음 train_test_split 함수를 사용하여 데이터와 타겟을 훈련 세트와 테스트 세트로 분할합니다.
그 다음 LinearRegression 클래스를 사용하여 훈련 데이터에 대한 선형 회귀 모델을 학습합니다. 그리고 훈련 세트와 테스트 세트에 대한 예측을 수행합니다.
Ridge 클래스를 사용하여 훈련 데이터에 대한 릿지 회귀 모델을 학습합니다. 그리고 훈련 세트와 테스트 세트에 대한 예측을 수행합니다.
마지막으로, 각 모델의 훈련 세트와 테스트 세트에 대한 평균 제곱 오차(Mean Squared Error, MSE)를 계산하고, 결과를 출력합니다.
즉, 이 코드는 선형 회귀 모델과 릿지 회귀 모델을 학습하고, 이들 모델의 성능을 평가하는 기본적인 머신 러닝 코드입니다.
전체코드는 다음과 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error
np.random.seed(2021)
#Load diabetes dataset
diabetes = load_diabetes()
data, target = diabetes["data"], diabetes["target"]
#Split data into training and test sets
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3)
#Train a linear regression model
multi_regressor = LinearRegression()
multi_regressor.fit(train_data, train_target)
#Make predictions on the training and test sets using the linear regression model
multi_train_pred = multi_regressor.predict(train_data)
multi_test_pred = multi_regressor.predict(test_data)
#Train a ridge regression model
ridge_regressor = Ridge()
ridge_regressor.fit(train_data, train_target)
#Make predictions on the training and test sets using the ridge regression model
ridge_train_pred = ridge_regressor.predict(train_data)
ridge_test_pred = ridge_regressor.predict(test_data)
#Calculate the mean squared error for both models on the training and test sets
multi_train_mse = mean_squared_error(multi_train_pred, train_target)
multi_test_mse = mean_squared_error(multi_test_pred, test_target)
ridge_train_mse = mean_squared_error(ridge_train_pred, train_target)
ridge_test_mse = mean_squared_error(ridge_test_pred, test_target)
#Print the mean squared errors
print(f"Linear Regression Train MSE is {multi_train_mse:.4f}")
print(f"Linear Regression Test MSE is {multi_test_mse:.4f}")
print(f"Ridge Regression Train MSE is {ridge_train_mse:.4f}")
print(f"Ridge Regression Test MSE is {ridge_test_mse:.4f}")LASSO Regression 학습
from sklearn.linear_model import Lasso
lasso_regressor = Lasso()
lasso_regressor.fit(train_data, train_target)회귀식 확인
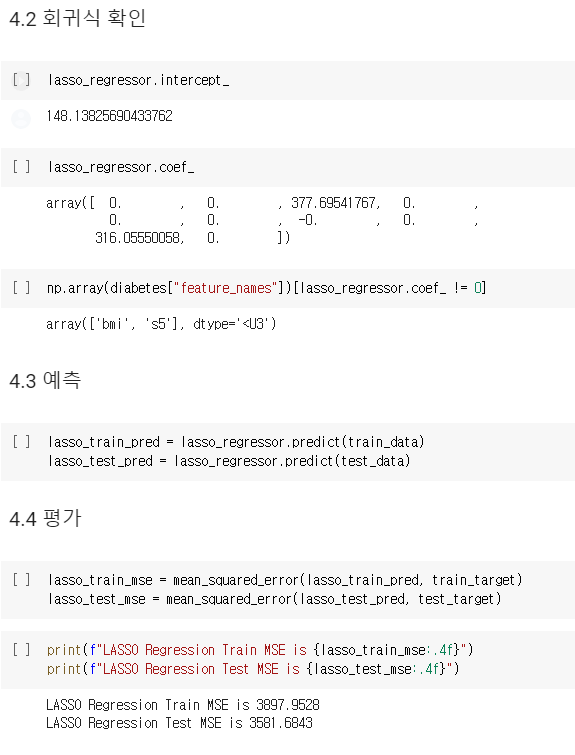
lasso_regressor.intercept_
lasso_regressor.coef_
np.array(diabetes["feature_names"])[lasso_regressor.coef_ != 0]예측
lasso_train_pred = lasso_regressor.predict(train_data)
lasso_test_pred = lasso_regressor.predict(test_data)평가
lasso_train_mse = mean_squared_error(lasso_train_pred, train_target)
lasso_test_mse = mean_squared_error(lasso_test_pred, test_target)
print(f"LASSO Regression Train MSE is {lasso_train_mse:.4f}")
print(f"LASSO Regression Test MSE is {lasso_test_mse:.4f}")즉 전체 코드는 아래와 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#Import necessary modules from scikit-learn
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error
#Set the random seed for reproducibility
np.random.seed(2021)
#Load the diabetes dataset
diabetes = load_diabetes()
data, target = diabetes["data"], diabetes["target"]
#Split the data into training and test sets using scikit-learn's train_test_split function
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3)
#Train a linear regression model on the training data
multi_regressor = LinearRegression()
multi_regressor.fit(train_data, train_target)
#Make predictions on the training and test sets using the linear regression model
multi_train_pred = multi_regressor.predict(train_data)
multi_test_pred = multi_regressor.predict(test_data)
#Train a LASSO regression model on the training data
lasso_regressor = Lasso()
lasso_regressor.fit(train_data, train_target)
#Print the intercept and coefficients of the LASSO regression model
print(f"LASSO Regression Intercept is {lasso_regressor.intercept_:.4f}")
print(f"LASSO Regression Coefficients are {lasso_regressor.coef_}")
#Print the feature names that have non-zero coefficients in the LASSO regression model
print(f"LASSO Regression Features are {np.array(diabetes['feature_names'])[lasso_regressor.coef_ != 0]}")
#Make predictions on the training and test sets using the LASSO regression model
lasso_train_pred = lasso_regressor.predict(train_data)
lasso_test_pred = lasso_regressor.predict(test_data)
#Calculate the mean squared error for the LASSO regression model on the training and test sets
lasso_train_mse = mean_squared_error(lasso_train_pred, train_target)
lasso_test_mse = mean_squared_error(lasso_test_pred, test_target)
#Print the mean squared error for the LASSO regression model on the training and test sets
print(f"LASSO Regression Train MSE is {lasso_train_mse:.4f}")
print(f"LASSO Regression Test MSE is {lasso_test_mse:.4f}")
이 코드는 scikit-learn 라이브러리를 사용하여 당뇨병 데이터셋에 대한 선형 회귀, 릿지 회귀, 라쏘 회귀 모델을 만들고, 훈련 및 테스트 데이터에서 평균 제곱 오차를 계산하는 것입니다.
코드는 다음과 같은 작업을 수행합니다.
pandas, numpy, matplotlib.pyplot 및 scikit-learn 라이브러리를 가져옵니다.
scikit-learn에서 load_diabetes() 함수를 사용하여 당뇨병 데이터셋을 가져옵니다.
train_test_split() 함수를 사용하여 데이터를 훈련 세트와 테스트 세트로 분할합니다.
LinearRegression() 함수를 사용하여 훈련 데이터에서 선형 회귀 모델을 학습합니다.
Lasso() 함수를 사용하여 훈련 데이터에서 라쏘 회귀 모델을 학습합니다.
mean_squared_error() 함수를 사용하여 훈련 및 테스트 데이터에서 모델의 평균 제곱 오차를 계산합니다.
결과를 출력합니다.
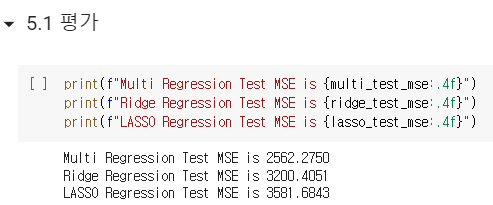
마무리(평가)
print(f"Multi Regression Test MSE is {multi_test_mse:.4f}")
print(f"Ridge Regression Test MSE is {ridge_test_mse:.4f}")
print(f"LASSO Regression Test MSE is {lasso_test_mse:.4f}")예측값과 실제값의 관계 Plot
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
preds = [
("Multi regression", multi_test_pred),
("Ridge regression", ridge_test_pred),
("LASSO regression", lasso_test_pred),
]
for idx, (name, test_pred) in enumerate(preds):
ax = axes[idx]
ax.scatter(test_pred, test_target)
ax.plot(np.linspace(0, 330, 100), np.linspace(0, 330, 100), color="red")
ax.set_xlabel("Predict")
ax.set_ylabel("Real")
ax.set_title(name)이 코드는 다중 선형 회귀 모델, 릿지 회귀 모델, LASSO 회귀 모델의 테스트 MSE를 계산하고, 각각의 모델이 만든 예측값과 실제값의 관계를 시각화하는 코드입니다.
먼저, print 함수를 사용하여 multi_test_mse, ridge_test_mse, lasso_test_mse의 값을 출력합니다. 각각 다중 선형 회귀 모델, 릿지 회귀 모델, LASSO 회귀 모델의 테스트 MSE입니다.
그리고 plt.subplots 함수를 사용하여 1행 3열의 그래프들을 생성하고, 각 모델의 이름과 테스트 데이터셋에서 생성된 예측값 multi_test_pred, ridge_test_pred, lasso_test_pred를 사용하여 산점도를 그리고, 빨간색으로 실제값과 예측값이 같은 선을 그려줍니다. 이를 통해 각 모델이 만든 예측값과 실제값의 관계를 시각적으로 확인할 수 있습니다.
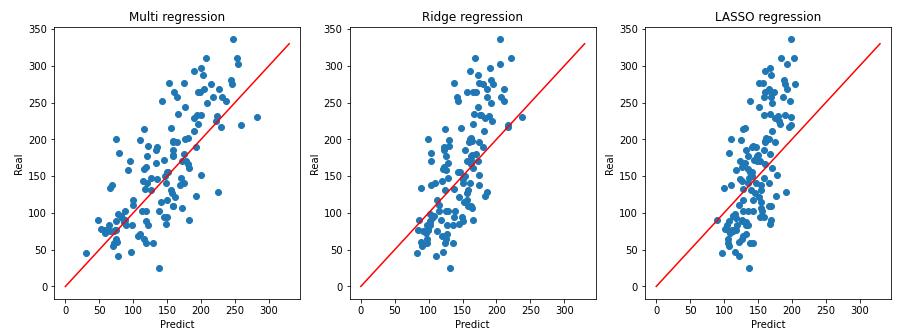
가로축은 예측값, 세로축은 실제값을 나타낸다.
따라서 전체 코드는 아래와 같다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error
np.random.seed(2021)
diabetes = load_diabetes()
data, target = diabetes["data"], diabetes["target"]
train_data, test_data, train_target, test_target = train_test_split(data, target, test_size=0.3)
multi_regressor = LinearRegression()
multi_regressor.fit(train_data, train_target)
multi_train_pred = multi_regressor.predict(train_data)
multi_test_pred = multi_regressor.predict(test_data)
ridge_regressor = Ridge()
ridge_regressor.fit(train_data, train_target)
ridge_train_pred = ridge_regressor.predict(train_data)
ridge_test_pred = ridge_regressor.predict(test_data)
lasso_regressor = Lasso()
lasso_regressor.fit(train_data, train_target)
lasso_train_pred = lasso_regressor.predict(train_data)
lasso_test_pred = lasso_regressor.predict(test_data)
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
preds = [
("Multi regression", multi_test_pred),
("Ridge regression", ridge_test_pred),
("LASSO regression", lasso_test_pred),
]
for idx, (name, test_pred) in enumerate(preds):
ax = axes[idx]
ax.scatter(test_pred, test_target)
ax.plot(np.linspace(0, 330, 100), np.linspace(0, 330, 100), color="red")
ax.set_xlabel("Predict")
ax.set_ylabel("Real")
ax.set_title(name)
plt.show()위 코드는 당뇨병 환자들의 데이터를 활용하여, 세 가지 모델(Multi regression, Ridge regression, LASSO regression)을 훈련하고, 테스트 데이터를 활용하여 예측 결과를 비교하는 과정을 보여주는 코드입니다.
코드를 보면, 먼저 데이터를 로드하고, 훈련 데이터와 테스트 데이터로 분리합니다. 그 다음으로, 세 가지 모델을 훈련시키고, 각 모델에서 테스트 데이터를 활용하여 예측 결과를 얻어냅니다.
이후에는 예측 결과를 시각화하여 모델들 간의 예측 결과를 비교합니다. 그래프의 가로축은 모델이 예측한 값, 세로축은 실제 값으로 설정하여, 빨간색 직선은 예측과 실제 값이 일치하는 경우를 나타냅니다.
