- 확률의 개념
- 특정한 사건이 일어날 가능성
조건부 확률
어떤 사건 A가 일어 났을 때, 다른 사건 B가 발생할 확률
P(B|A) = P(A ∩ B) / P(A)조건부 확률 곱셈 공식
P(A ∩ B) = P(A|B) x P(B) = P(B|A) x P(A)P(A ∩ B)는 A와 B가 동시에 일어날 확률을 의미하며,
P(A|B)는 B가 일어난 조건에서 A가 일어날 확률을 의미한다.
P(B|A)는 A가 일어난 조건에서 B가 일어날 확률을 의미하며,
P(A)와 P(B)는 각각 A와 B가 일어날 확률을 의미!
독립 (두 사건이 서로 영향을 주지 않는 관계를 의미)
사건 A가 일어나는 것에 상관없이 사건 B가 일어날 확률이 일정할 때
(=A가 일어나는 것이 사건 B가 일어날 확률에 영향을 주지 않는 경우)
P(A ∩ B) = P(A)P(B)조건부 독립
사건 C가 일어났을 때 서로 다른 사건 A, B가 독립일 때
(=사건 C가 주어졌을 때, 사건 A와 사건 B가 동시에 일어날 확률을 나타내는 식)
P(A,B|C) = P(A|C)P(B|C)은 사건 A와 사건 B가 독립이 아닌 경우에는 성립하지 않는다.
P(A,B|C) = P(A|C) = P(B|C)
- 베이즈 정리
- 조건부 확률의 공식 중 하나로,
이전에 얻은 정보를 바탕으로 새로운 정보를 예측하는 데 사용된다.
베이즈 정리의 수식
P(A|B) = P(B|A)P(A) / P(B)
A와 B는 두 개의 사건이다.
P(A|B)는 B가 주어졌을 때 A가 일어날 조건부 확률을 의미합니다.
이 값을 구하기 위해서는 이전에 얻은 정보 P(A)와 B가 일어날 확률 P(B)가 필요합니다.
P(B|A)는 A가 주어졌을 때 B가 일어날 확률을 의미합니다.
이 값을 사전 확률 또는 prior probability라고 하며, 베이즈 정리에서는 새로운 정보를 통해 이전에 가지고 있던 사전 확률을 수정합니다.
베이즈 정리는 주로 확률론, 통계학, 인공지능 분야에서 사용됩니다.
예를 들어, 스팸 메일 필터링에서는 베이즈 정리를 사용하여 이전에 스팸으로 분류되었던 메일들의 정보를 바탕으로 새로운 메일이 스팸인지 아닌지를 예측합니다.
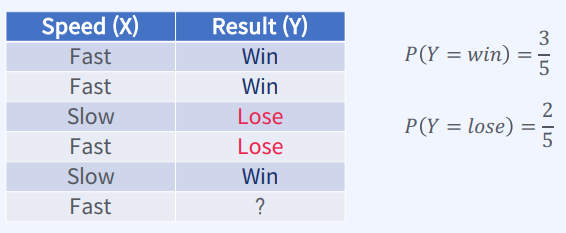
주어진 데이터에서 X는 선수의 속도(Fast 또는 Slow)를
Y는 경기 결과(Win 또는 Lose)를 나타냅니다.
마지막 행에서는 X가 Fast일 때 Y가 무엇일지 예측해야 합니다.
베이즈 정리를 이용하여 문제를 풀 수 있습니다. 다음과 같은 가정을 합니다.
P(X=Fast) = 0.6 (전체 선수 중 60%가 Fast)
P(X=Slow) = 0.4 (전체 선수 중 40%가 Slow)
P(Y=Win|X=Fast) = 0.75 (Fast 선수 중 75%가 이기는 경우)
P(Y=Win|X=Slow) = 0.25 (Slow 선수 중 25%가 이기는 경우)
이를 바탕으로 P(Y=Win|X=Fast)와 P(Y=Lose|X=Fast)를 계산할 수 있습니다.
P(Y=Win|X=Fast) = 0.75
P(Y=Lose|X=Fast) = 1 - P(Y=Win|X=Fast) = 0.25
따라서, 마지막 행에서 X가 Fast일 때 Y가 Win일 확률은 다음과 같이 계산할 수 있습니다.
P(X=Fast|Y=Win) = P(Y=Win|X=Fast)P(X=Fast) / [P(Y=Win|X=Fast)P(X=Fast) + P(Y=Win|X=Slow)P(X=Slow)]
= (0.75 x 0.6) / [(0.75 x 0.6) + (0.25 x 0.4)]
= 0.818
따라서, X가 Fast일 때 Y가 Win일 확률은 약 0.818 또는 81.8%입니다.
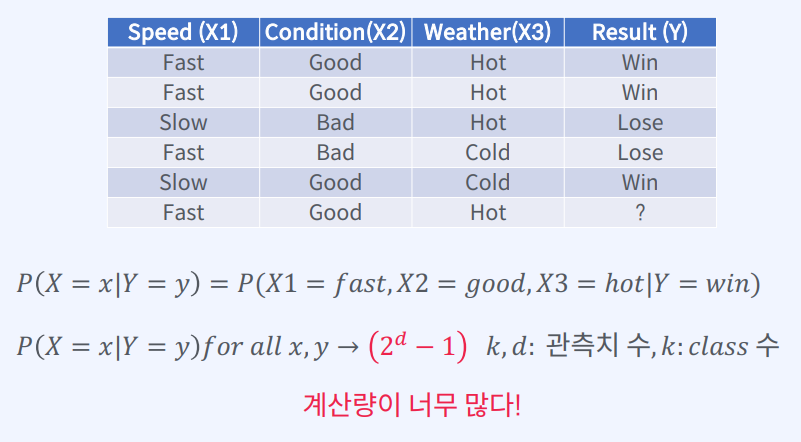
- Naive Bayes
- 종속 변수(Y)가 주어졌을 때 입력 변수(X)들은 모두 조건부 독립이다.
- 예측 변수들의 정확한 조건부 확률은 각 조건부 확률의 곱으로 충분히 잘 추정 할 수 있다는 단순한 가정
- 데이터셋을 순진하게 믿는다! -> Naïve(순진한) Bayes!
Naive Bayes는 각 입력 변수가 서로 독립이라는 가정을 기반으로 하며, 모든 입력 변수들이 종속 변수에 대해 동일한 기여도를 가진다고 가정합니다.
이러한 가정은 실제 데이터에서는 항상 성립하지 않을 수 있지만,
일반적으로는 효과적인 분류 모델을 생성하는 데 사용됩니다.
이 모델은 각 클래스(종속 변수)에 대한 사전 확률과 각 입력 변수가 클래스를 예측하는 데 얼마나 유용한지를 나타내는 조건부 확률을 학습하여 생성됩니다.
Naive Bayes는 간단하고 빠르게 학습할 수 있으며, 작은 데이터셋에서도 잘 작동하는 것으로 알려져 있습니다.

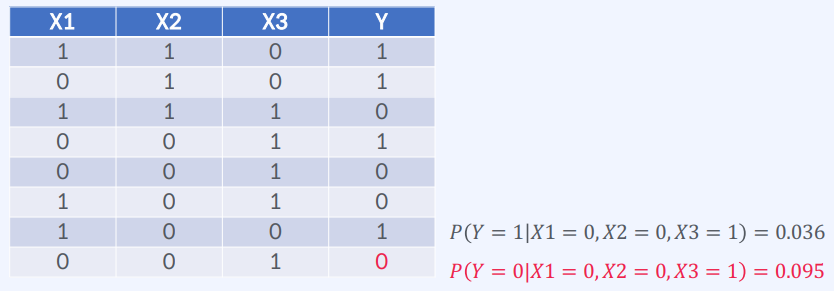
종속 변수 Y와 입력 변수 X1, X2, X3으로 구성된 데이터셋
이 데이터셋을 Naive Bayes 분류 모델을 학습하기 위해 사용할 수 있다.
Naive Bayes 분류 모델을 학습하기 위해서는 먼저 각 클래스(종속 변수)의 사전 확률을 계산해야 합니다.
이 데이터셋에서는 Y가 0인 경우와 Y가 1인 경우가 모두 16개씩 있으므로, 각 클래스의 사전 확률은 0.5입니다.
다음으로, 각 입력 변수(X1, X2, X3)가 주어졌을 때, 클래스(종속 변수)를 예측하는 데 얼마나 유용한지를 나타내는 조건부 확률을 계산해야 합니다.
이 데이터셋에서는 입력 변수들이 이진 변수(binary variable)로 되어 있으므로, 조건부 확률은 베르누이 분포를 사용하여 계산할 수 있습니다.
가령, X1=1이 주어졌을 때 Y=1일 확률을 계산하려면, 다음과 같은 식을 사용할 수 있습니다.
P(Y=1 | X1=1) = P(X1=1 | Y=1) * P(Y=1) / P(X1=1)위 식에서 P(X1=1 | Y=1)는 Y=1일 때 X1=1일 확률을 의미합니다.
이 데이터셋에서는 Y=1일 때 X1=1인 경우가 6개이므로, P(X1=1 | Y=1) = 6/16 = 0.375입니다.
P(Y=1)은 위에서 구한 것처럼 0.5입니다.
P(X1=1)은 X1=1인 경우의 전체 개수(12개)를 데이터셋 전체 개수(32개)로 나눈 값인 0.375입니다.
따라서, P(Y=1 | X1=1) = 0.375 * 0.5 / 0.375 = 0.5입니다.
이와 같은 방법으로, X2와 X3에 대한 조건부 확률을 구하여 Naive Bayes 분류 모델을 학습할 수 있습니다.
아래는 이와 같은 문제를 방지하기 위해 사용되는 방법 중 하나이다!
예를 들어, 베이지안 분류기에서 학습 데이터셋에 포함되지 않은 단어가 나타나는 경우 해당 단어의 확률은 0이 되어 분류기가 예측을 할 수 없게 됩니다.
Laplace Smoothing은 이를 방지하기 위해 해당 단어가 나타난 적이 없더라도 최소한의 확률을 할당해주는 방식으로 이를 해결합니다.
이 방법은 가장 단순한 방법 중 하나이며, 일반적으로는 Add-k Smoothing과 같은 더 복잡한 방법들이 사용되기도 합니다.
Laplace Smoothing
- Count하다 보면 한 번도 나오지 않는 경우도 있을 수 있다.
-> 확률이 0이 되는 것을 방지해야 함 - 최소한의 확률을 정해 준다
P(x_i | y) = (count(x_i, y) + 1) / (count(y) + |V|)여기서,
x_i: i번째 단어 (입력 변수)
y: 클래스 (종속 변수)
count(x_i, y): 학습 데이터셋에서 y 클래스에 속하며 x_i 단어가 나타난 횟수
count(y): 학습 데이터셋에서 y 클래스에 속한 문서의 총 개수
|V|: 단어장(vocabulary)의 크기 (중복을 제거한 단어의 총 개수)
즉, Laplace Smoothing은 모든 단어가 한 번 이상 나타난 것으로 가정하고, count(x_i, y)에 1을 더한 값으로 분자를 조정하고, 분모에는 전체 단어의 수(|V|)를 더한 값으로 정규화합니다. 이를 통해 모든 단어가 최소한 일정한 확률을 가지도록 보장할 수 있습니다.
1. Naive Bayes 장점
-
변수가 많을 때에도 높은 정확도를 보인다
: Naive Bayes는 변수들 간의 조건부 독립을 가정하기 때문에 변수가 많더라도 계산이 상대적으로 간단하다는 장점 -
텍스트 데이터에서 좋은 성능을 보인다
: Naive Bayes는 자연어 처리 분야에서 높은 정확도를 보이는 분류 알고리즘 중 하나입니다.
단어와 문장 등의 텍스트 데이터를 분석하여 주제나 감성 등을 판별할 때 자주 사용됩니다.
2. Naive Bayes 단점
-
희귀한 확률값 처리가 어려울 수 있다
: 학습 데이터셋에서 특정 변수의 값이 한 번도 나타나지 않는 경우에는 확률 계산 과정에서 분모가 0이 되어버리는 문제가 발생할 수 있습니다.
이를 해결하기 위해 Laplace Smoothing과 같은 기법을 사용할 수 있습니다. -
조건부 독립 가정이 비현실적일 수 있다
: Naive Bayes는 입력 변수들 간의 조건부 독립을 가정하기 때문에, 실제 데이터에서는 서로 관련된 변수들이 많이 존재하는 경우가 많습니다. 따라서, 이러한 경우에는 다른 분류 알고리즘을 사용하는 것이 더 적합할 수 있습니다.
