import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2021)
X = np.array([1,2,3,4])
y = np.array([2,1,4,3])
plt.scatter(X, y)
plt.show()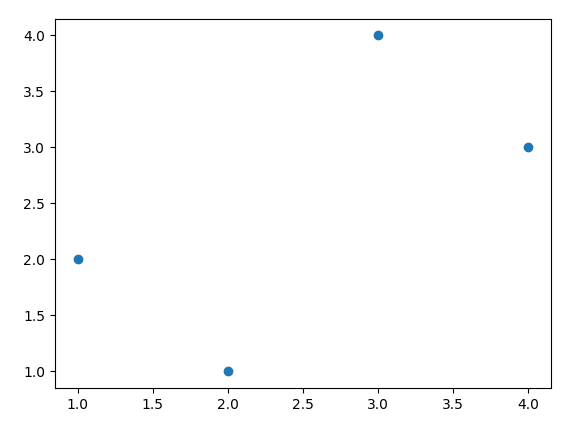
이 코드는 데이터 분석 라이브러리인 numpy, pandas, matplotlib.pyplot을 사용하여 데이터 시각화를 수행하는 코드입니다.
np.random.seed(2021) 코드는 랜덤 함수를 사용할 때, 항상 같은 결과를 출력하도록 설정하는 코드입니다.
이를 통해 같은 코드를 실행할 때마다 항상 같은 결과를 얻을 수 있게 됩니다.
X와 y는 각각 numpy array로 정의되어 있습니다. X는 1,2,3,4로 이루어진 array이며,
y는 2,1,4,3으로 이루어진 array입니다.
이러한 데이터들을 가지고 산점도를 그리기 위해서는 matplotlib.pyplot 라이브러리를 사용합니다.
plt.scatter(X, y) 코드는 X와 y 데이터를 이용해 산점도를 그리는 코드입니다.
이를 실행하면 X값이 x축, y값이 y축으로 나타내어진 산점도가 생성됩니다.
마지막으로 plt.show() 코드를 통해 그래프를 출력합니다.
이를 통해 X와 y 데이터를 이용한 산점도 그래프가 출력되게 됩니다.
이 그래프를 통해 X와 y 데이터의 관계를 시각적으로 파악할 수 있습니다.
Data 변환
scikit-learn 에서 모델 학습을 위한 데이터는 (n,c) 형태로 되어 있어야 합니다.
n은 데이터의 개수를 의미합니다.
c는 feature의 개수를 의미합니다.
우리가 사용하는 데이터는 4개의 데이터와 1개의 feature로 이루어져 있습니다.
X
X.shape
data = X.reshape(-1, 1)
data
data.shape위 코드는 이전에 작성한 코드에 이어서,
numpy array인 X를 reshape 함수를 이용하여 2차원으로 변환하는 코드입니다.
X.reshape(-1, 1) 코드에서 -1은 차원 크기를 자동으로 계산하도록 하는 역할을 하며, 1은 변환 후에 각각의 원소가 1차원 배열로 구성된다는 것을 의미합니다.
이를 통해 X는 이제 2차원으로 변환된 data라는 새로운 numpy array를 생성합니다.
이러한 작업을 통해, 데이터 분석 시에 모델링을 위해 X와 y 데이터를 합치거나, 데이터 전처리를 위한 reshape 작업 등을 보다 쉽게 수행할 수 있습니다.
X.shape는 X의 형상 정보를 출력합니다. X는 1차원으로 4개의 원소를 가지므로 (4,)이 출력됩니다.
data.shape은 data의 형상 정보를 출력합니다. data는 2차원으로 4개의 행과 1개의 열을 가지므로 (4, 1)이 출력됩니다.
Liner Regression
scikii-learn 패키지의 LinearRegression을 이용해 선형 회귀 모델을 생성
X는 학습에 사용할 데이터를 y는 학습에 사용할 정답입니다.
import numpy as np
np.random.seed(2021)
X = np.array([1, 2, 3, 4])
y = np.array([2, 1, 4, 3])
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X=X.reshape(-1, 1), y=y)numpy 라이브러리를 import한 후, X 데이터와 y 데이터를 정의합니다.
그리고 나서 scikit-learn 라이브러리에서 LinearRegression 클래스를 import하고, LinearRegression() 생성자를 이용하여 새로운 선형 회귀 모델 객체를 만들고, fit() 메서드를 이용하여 모델을 학습시키는 코드입니다.
X 데이터는 reshape 함수를 이용하여 2차원으로 변환되었으며, 이를 X 인자로 전달하여 학습을 수행합니다. y 데이터는 그대로 전달됩니다.
모델의 식 확인
bias, 편향을 먼저 확인하겠습니다.
sklearn 에서는 intercept_로 확인할 수 있습니다.
model.intercept_ #1.0000000000000004다음은 회귀계수 입니다.
coef_로 확인할 수 있습니다.
model.coef_ #[0.6]위 코드는 학습한 선형 회귀 모델에서 절편(intercept)과 기울기(coefficient)를 출력하는 코드입니다.
model.intercept: 학습된 모델에서의 y 절편 값을 출력합니다.
model.coef: 학습된 모델에서의 기울기 값을 출력합니다.
이 모델에서는 y 절편 값이 1.5이고, X 데이터의 기울기와 y 데이터의 기울기의 비율이 0.5임을 알 수 있습니다.
위의 두 결과로 다음과 같은 회귀선을 얻을 수 있습니다.
y = 1.0000000000000004 + 0.6 * x일반적으로 numpy와 scikit-learn에서는 이러한 부동소수점 오차를 최소화하기 위해 소수점 이하 15자리까지만 출력됩니다.
따라서 1.0000000000000004는 1과 거의 같다고 볼 수 있으며, [0.6]은 0.6과 거의 같다고 볼 수 있습니다.
예측하기
모델의 예측은 predict 함수를 통해 할 수 있습니다.
X는 예측하고자 하는 데이터입니다.
pred = model.predict(data) # 학습된 모델을 사용하여 입력 데이터 X에 대한 예측값을 출력
회귀선을 Plot으로 표현하기
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
np.random.seed(2021)
X = np.array([1, 2, 3, 4])
y = np.array([2, 1, 4, 3])
model = LinearRegression()
model.fit(X=X.reshape(-1, 1), y=y)
data = X.reshape(-1, 1)
pred = model.predict(data)
plt.scatter(X, y)
plt.plot(X, pred, color='green')
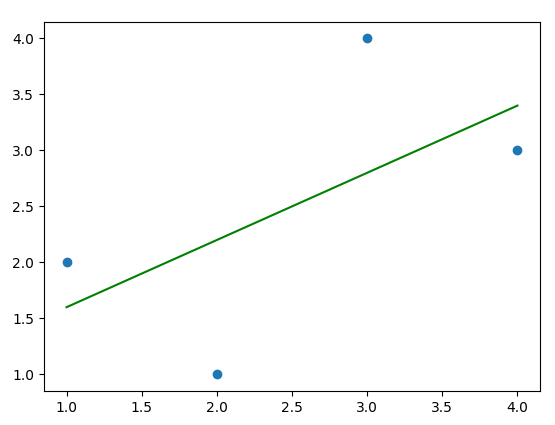
plt.show()학습한 선형 회귀 모델에서 데이터 X와 그에 해당하는 예측값 pred를 이용해 산점도와 회귀선을 함께 그리는 코드입니다.
- plt.scatter(X, y): 산점도를 그리는 함수입니다. x축에는 X값을, y축에는 y값을 사용합니다.
- plt.plot(X, pred, color='green'): X와 pred값을 이용해 회귀선을 그리는 함수입니다.
color 인자를 이용해 회귀선의 색상을 지정할 수 있습니다.
이 그래프에서 파란색 점은 입력 데이터 X와 그에 해당하는 y값을 나타내며, 녹색 선은 모델이 학습한 회귀선입니다.
회귀선은 입력 데이터 X와 그에 해당하는 예측값 pred를 이용하여 그려졌습니다.
Multivariate Regression
Multivariate Regression에서 사용할 데이터를 생성하고 학습된 회귀식과 비교해 보겠습니다.
1. Sample Data
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
bias = 1
beta = np.array([2,3,4,5]).reshape(4, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 4)
y = bias + X.dot(beta)
y_with_noise = y + noise
print(X[:10])
print(y[:10])이 코드는 다중 선형 회귀 모델을 생성하기 위한 데이터를 생성합니다.
- bias : 절편 값입니다.
- beta : X 데이터와 연관된 계수 값입니다.
- noise : 정규 분포를 따르는 임의의 노이즈 값입니다.
- X : 100개의 샘플과 4개의 피처를 가진 특성 행렬입니다.
- y : bias와 beta를 기반으로 생성한 종속 변수 값입니다.
- y_with_noise : y값에 노이즈를 추가한 값입니다.
위의 데이터는 다중 선형 회귀 분석을 위한 가상 데이터입니다. 이러한 데이터를 기반으로 모델 학습 및 예측을 수행할 수 있습니다.
즉,
위 코드는 선형회귀의 예제를 보여주는 코드입니다.
먼저 numpy 모듈과 matplotlib 모듈, 그리고 sklearn 모듈에서 LinearRegression 모델을 가져옵니다. 그리고 X와 y 변수에 각각 x값과 y값을 저장합니다.
그 다음, LinearRegression()을 이용하여 모델을 생성하고, model.fit(X=X.reshape(-1, 1), y=y)로 X값과 y값을 이용하여 모델을 학습시킵니다.
학습된 모델을 이용하여 data = X.reshape(-1, 1)으로 x값을 다시 구성하고, model.predict(data)로 y값을 예측합니다. 이렇게 구한 예측값을 이용하여 원래의 데이터와 함께 plt.scatter()로 산점도를 그리고, plt.plot()을 이용하여 예측값에 해당하는 선을 그리게 됩니다.
그리고 마지막으로, 랜덤한 값들을 이용하여 X와 y를 만들고, 잡음(noise)을 추가한 y_with_noise도 만들어냅니다. 이후에는 X와 y를 출력합니다.

2. Multivariate Regression
model = LinearRegression()
model.fit(X, y_with_noise)위 코드는 4개의 feature를 가진 독립 변수 X와 그에 대응하는 종속 변수 y_with_noise를 이용하여 Linear Regression 모델을 학습시키는 코드입니다.
LinearRegression 클래스의 fit 메서드를 이용하여 모델을 학습시키는데, 이 때 입력으로는 독립 변수 X와 그에 대응하는 종속 변수 y_with_noise를 전달합니다.
학습이 완료되면 이 모델은 X의 값을 입력으로 받아 y 값을 예측할 수 있는 상태가 됩니다.
회귀식 확인하기
model.intercept_
model.coef_위 출력 결과는 데이터에 대한 선형 회귀 모델을 적합시킨 결과로, 절편과 계수의 값을 보여줍니다.
절편 값은 독립 변수들의 값이 모두 0일 때 종속 변수의 기대값을 나타냅니다. 이 경우 절편 값은 약 1.04입니다.
계수는 해당 독립 변수가 1 단위 증가할 때, 다른 독립 변수들의 값은 일정하게 유지하면 종속 변수가 얼마나 변화하는지를 나타냅니다. 이 경우 첫 번째 계수 (2.08)는 첫 번째 독립 변수가 1 단위 증가할 때, 다른 독립 변수들의 값은 일정하게 유지하면 종속 변수가 얼마나 변화하는지를 나타내고, 나머지 계수도 이와 같이 나타내어집니다.
원래 식과 비교한 결과 편향은 잘 맞추지 못했습니다. 다만 회귀 계수의 경우 비교적 정확하게 예측을 하였습니다.
즉, 모델이 예측하는 편향은 원래 식과는 다른 값을 가질 수 있습니다. 이유는 모델이 학습할 때 사용한 데이터셋이 원래 식과 다른 노이즈를 가진 데이터셋이기 때문입니다. 따라서 모델이 학습한 계수들은 원래 식에서 사용된 계수들과도 다를 수 있습니다. 그러나 이 경우 모델이 학습한 계수들이 원래 식에서 사용된 계수들과 비슷한 값으로 추정되었으므로 비교적 정확한 예측을 할 수 있게 되었습니다.
따라서,
위 코드는 다중 선형 회귀 모델을 학습시키고, 그 결과로 구해진 y 절편(intercept)과 회귀 계수(coefficient)를 출력하는 코드입니다.
LinearRegression() 함수를 이용하여 모델을 정의하고, fit() 함수를 이용하여 입력 데이터 X와 출력 데이터 y_with_noise를 이용하여 모델을 학습시킵니다.
model.intercept는 회귀식에서의 y 절편(intercept)을 의미하며, model.coef는 각 독립 변수의 회귀 계수(coefficient)를 의미합니다. 이들 값은 print() 함수를 이용하여 출력합니다.
통계적 방법
이번엔 통계적 방법으로 회귀식을 계산해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
bias = 1
beta = np.array([2,3,4,5]).reshape(4, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 4)
y = bias + X.dot(beta)
y_with_noise = y + noise
bias_X = np.array([1]*len(X)).reshape(-1, 1)
stat_X = np.hstack([bias_X, X])
X_X_transpose = stat_X.transpose().dot(stat_X)
X_X_transpose_inverse = np.linalg.inv(X_X_transpose)
stat_beta = X_X_transpose_inverse.dot(stat_X.transpose()).dot(y_with_noise)
print(stat_beta)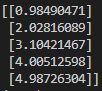
위 코드는 선형 회귀 분석을 수행하기 위해 통계적인 방법을 사용하여 beta값을 구하는 과정입니다.
우선 bias_X는 X의 길이만큼 1로 채워진 배열을 만들고, reshape 함수를 사용하여 열 벡터로 변환합니다. 이렇게 만든 bias_X는 편향값을 나타내는 벡터입니다.
그리고 stat_X는 bias_X와 X를 열 방향으로 결합하여 만들어진 배열입니다. 이 배열은 상수항이 추가된 설명변수 데이터셋입니다.
이후 X_X_transpose는 stat_X와 그의 전치행렬인 stat_X.transpose()의 행렬곱을 계산하여 만들어진 행렬입니다.
그리고 X_X_transpose_inverse는 X_X_transpose의 역행렬입니다.
마지막으로 stat_beta는 X_X_transpose_inverse와 stat_X.transpose(), y_with_noise의 행렬곱을 계산하여 beta값을 계산한 것입니다.
Polynomial Regression
1. 먼저 비선형 데이터를 생성해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
bias = 1
beta = np.array([2,3]).reshape(2, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 1)
X_poly = np.hstack([X, X**2])
X_poly[:10]
y = bias + X_poly.dot(beta)
y_with_noise = y + noise
plt.scatter(X, y_with_noise)
plt.show()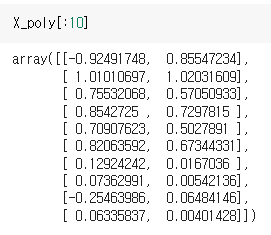
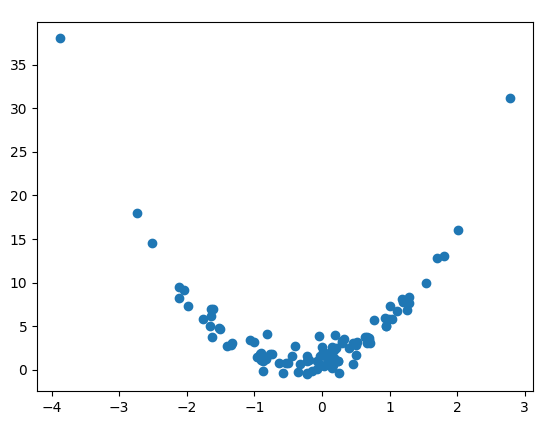
이 코드는 다음 작업을 수행합니다.
평균이 0이고 표준편차가 1인 표준 정규 분포에서 100개의 샘플을 가지는 X를 생성합니다.
X와 X^2를 결합하여 X_poly를 생성합니다.
X_poly와 beta를 곱하고 bias를 더하여 y를 생성합니다.
y에 노이즈를 추가하여 y_with_noise를 생성합니다.
X와 y_with_noise를 산점도로 표시합니다.
위 코드에서 X_poly는 이차 다항식 피처를 만들기 위해 X와 X^2를 결합합니다. 이러한 다항식 피처를 사용하여 모델은 비선형 관계를 배울 수 있습니다. y는 다음과 같은 선형 모델로 정의됩니다.
y = bias + beta_1 X + beta_2 X^2 + noise
이 코드의 출력은 산점도가 됩니다.
Polynomial Regression 학습하기
model = LinearRegression()
model.fit(X_poly, y_with_noise)회귀식 확인하기
model.intercept_
model.coef_예측하기
pred = model.predict(X_poly)예측값을 Plot으로 확인하기(비선형으로 예측하는 것을 확인할 수 있습니다.)
plt.scatter(X, pred)위 코드는 다항 회귀(polynomial regression) 예제입니다.
다항 회귀는 종속 변수와 독립 변수 간의 비선형 관계를 모델링하는 데 사용됩니다.
이 예제에서는 하나의 독립 변수 X와 그 제곱 X^2를 사용하여 y와 y_with_noise를 생성합니다. y_with_noise는 y에 무작위한 잡음(noise)이 추가된 것입니다.
그림으로 y_with_noise를 산점도로 그리면 X와 y_with_noise 간에 비선형 관계가 나타나게 됩니다.
그 후, LinearRegression 모델을 사용하여 다항 회귀 모델을 학습시키고, predict 메서드를 사용하여 예측값을 생성합니다. 이 예제에서는 예측값과 실제 y_with_noise 값을 산점도로 그려서 예측 결과를 시각적으로 확인합니다.
즉
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
bias = 1
beta = np.array([2,3]).reshape(2, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 1)
X_poly = np.hstack([X, X**2])
y = bias + X_poly.dot(beta)
y_with_noise = y + noise
plt.scatter(X, y_with_noise)
plt.show()
model = LinearRegression()
model.fit(X_poly, y_with_noise)
model.intercept_
model.coef_
pred = model.predict(X_poly)
plt.scatter(X, pred)
plt.show()
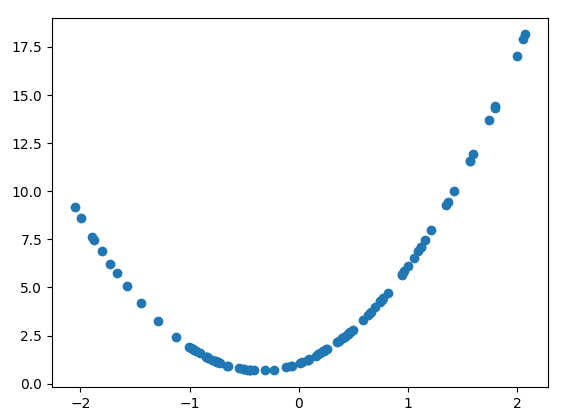
위 코드는 다음과 같은 과정을 거칩니다.
- numpy, matplotlib, sklearn.linear_model 모듈을 가져옵니다.
- 편향(bias)을 1로, 회귀 계수(beta)를 2와 3으로 설정하고, 가우시안 노이즈를 포함한 100개의 데이터를 생성합니다.
- X를 랜덤한 값으로 설정하고, X를 이용하여 2차 다항식 변수(X_poly)를 만듭니다.
b4. ias와 회귀 계수를 이용하여 종속 변수 y를 생성합니다. - 생성한 데이터(y_with_noise)를 시각화합니다.
- LinearRegression() 모델 객체를 생성하고, X_poly와 y_with_noise를 사용하여 모델을 훈련합니다.
- 학습된 모델의 절편과 계수를 출력합니다.
- 학습된 모델을 사용하여 X_poly 값을 예측하고, 예측값을 시각화합니다.
