선형 회귀(Linear Regression)의 정의
- 예측 값을 직선으로 표현하는 모델
- 하나의 독립 변수와 하나의 종속 변수 간의 선형 관계를 모델링하는 데 사용되는 기계 학습 기법
선형 회귀 수식
y = b0 + b1 * x- y는 종속 변수 (예측하려는 값)
- x는 독립 변수 (예측에 사용되는 값)
- b0는 y절편 (y가 x=0일 때의 y 값)
- b1은 기울기 (y값이 x 증가에 대해 얼마나 변화하는지를 나타내는 값)

회귀 모델에서는 학습 데이터에서 독립 변수와 종속 변수의 쌍을 사용하여 b0와 b1 값을 추정한다.
이를 통해 새로운 독립 변수 값을 사용하여 종속 변수 값을 예측할 수 있다.
편향
- 그래프에서 회귀선의 위치
- X가 0일 때의 예측 값
- 즉, 편향(bias)은 회귀 모델에서 y절편을 나타내며, 그래프에서 회귀선의 위치를 결정
x가 0일 때의 예측 값은 편향 값과 일치한다.
B1(계수, Coefficient)
- 회귀선의 기울기
- X가 1 증가할 때 예측 값이 증가하는 정도 (사람이 해석하기 좋다 = 해석이 용이)
- 모델의 입력 변수 중 하나의 영향력을 설명하기에 적합
- 이는 해석이 용이하며, 다른 입력 변수들과의 상호작용을 통해 모델의 예측력을 높일 수 있다.
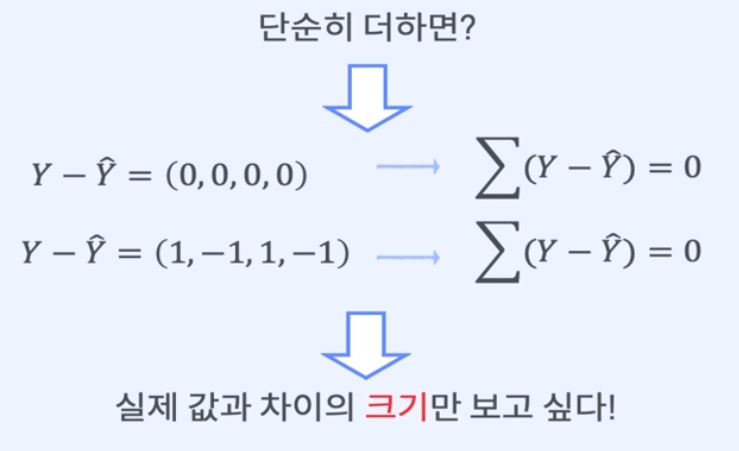
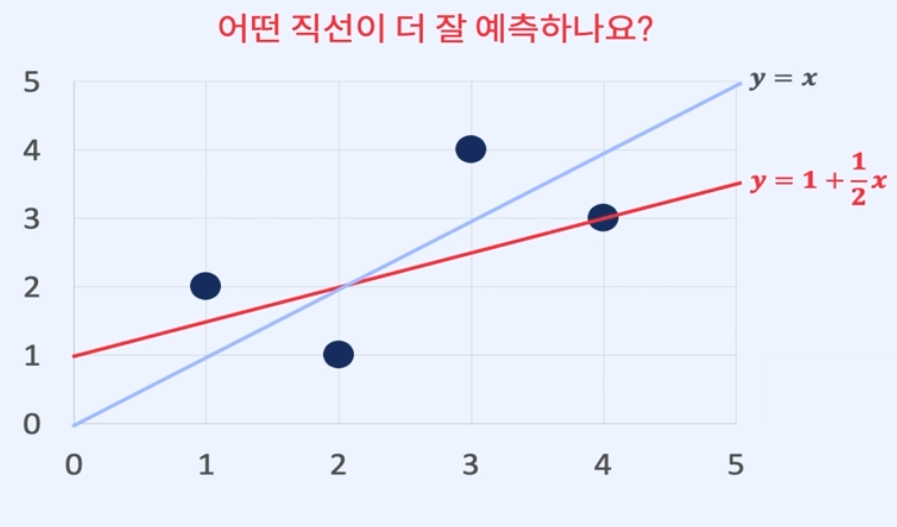
어떤 직선이 더 잘 예측하나요? = 실체 값과 예측 값의 차이가 작은 직선이 더 잘 예측한다!
이러한 차이를 잔차(residual)라고 하며, 예측 값과 실제 값의 차이를 최소화하는 방향으로 모델을 학습시킨다.
이를 최소제곱법(least squares method)이라고 하며, 이 방법은 잔차의 제곱 합을 최소화하는 회귀 직선을 찾는 것이다.
따라서, 모델의 성능을 평가할 때에는 잔차를 사용하여 실제 값과 예측 값의 차이를 계산하고, 이를 최소화하는 모델을 선택하는 것이 중요하다.



Mean Squared Error(MSE)
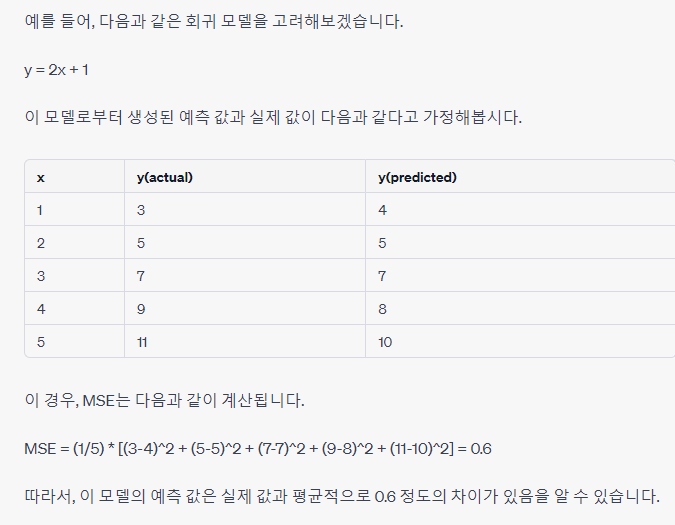
회귀 모델의 성능을 평가하기 위한 지표 중 하나로, 실제 값과 모델의 예측 값 사이의 차이를 제곱한 후 평균을 구한 값이다.
MSE가 작을수록 모델이 더 좋은 예측을 한다고 판단할 수 있다.
MSE = (1/n) * Σ(yi - ŷi)^2- n은 데이터의 개수
- yi는 i번째 데이터의 실제 값
- ŷi는 i번째 데이터의 모델 예측 값
다변량 회귀(Multivariate Regression)의 정의
: 두 개 이상의 변수로 만든 회귀식
즉, 두 개 이상의 독립 변수를 사용하여 종속 변수를 예측하는 회귀 분석 기법이다.
이를 이용하여 여러 개의 입력 변수가 종속 변수에 영향을 미치는 경우, 입력 변수들 간의 상호작용을 고려하여 예측 모델을 구성할 수 있다.
예를 들어, 다음과 같은 다변량 회귀 모델을 고려해보자!
y = β0 + β1x1 + β2x2 + ε이 경우, y는 종속 변수이며, x1과 x2는 독립 변수이다.
β0는 절편, β1과 β2는 각 독립 변수의 가중치(coefficient)로서, 회귀 모델에서 각 독립 변수가 종속 변수에 미치는 영향력을 나타낸다.
ε는 오차 항으로, 회귀 분석에서는 종종 오차항이 가우시안 정규 분포를 따른다는 가정을 따른다.
이러한 다변량 회귀 모델을 통해, 두 개 이상의 입력 변수들 간의 관계를 파악하고, 이를 이용하여 종속 변수를 예측하는데 활용할 수 있다.
다변량 회귀 수식
- 변수가 2개 인 경우
y = β0 + β1x1 + β2x2 + ε- 변수가 여러 개인 경우
-> 행렬로 표시
-> 3개의 변수를 가진 경우, 다음과 같이 행렬식으로 표현할 수 있다.
Y = Xβ + ε여기서,
- Y는 종속 변수를 나타내는 n차원의 열 벡터(n은 샘플 데이터의 개수)
- X는 독립 변수들의 값들을 가지고 있는 n x (p+1) 차원의 행렬(p는 독립 변수의 개수)
β- 는 모델 파라미터(계수)를 나타내는 (p+1)차원의 열 벡터
이는 X와 Y의 관계를 설명하는 모델의 파라미터를 나타낸다. - β0은 절편을 나타내며, β1, β2, ..., βp는 각각의 독립 변수의 가중치를 나타낸다.
- ε는 오차 항(error term)을 나타내며, 정규 분포를 따르는 랜덤 변수이다.
이는 모델로부터 예측되지 않는 잔차(residual)를 나타낸다.
따라서, 다음과 같이 행렬식으로 표현할 수 있다.

주어진 회귀식 y = 1 + 1/2 × X2 + 2X1에 대해 각 독립 변수의 계수를 해석하면 다음과 같다.
X1: 1 증가할 때, y는 2씩 증가 (B1 = 2)
X2: 1 증가할 때, y는 0.5씩 증가 (B2 = 0.5)
따라서, X2가 1 증가할 때, y의 예측값은 0.5만큼 증가
이와 마찬가지로, X1이 1 증가할 때, y의 예측값은 2만큼 증가
또한, 계수 B1과 B2를 비교하면, X2의 계수인 B2가 X1의 계수인 B1보다 작기 때문에 X2가 Y에 덜 영향을 미친다고 할 수 있다.
즉, X1이 Y에 더 큰 영향을 미친다.
다항식 회귀 (Polynomial Regression)
: 예측하는 값이 선형이 아닌 비선형일 경우 사용
선형 회귀 분석은 독립 변수와 종속 변수 간의 관계가 일차식(직선)인 경우에 사용된다.
하지만, 실제 데이터에서는 종종 선형적인 관계가 아닌 비선형적인 관계가 있기 때문에, 이런 경우에는 다항식 회귀를 사용하여 모델링을 수행한다.
다항식 회귀는 독립 변수 x의 거듭제곱을 새로운 변수로 추가하여
다음과 같은 일반적인 회귀식을 사용한다.
y = b0 + b1x + b2x^2 + ... + bnx^n여기서 x^2, x^3과 같이 x의 거듭제곱을 새로운 변수로 추가하여 사용하는 것이 특징!
이러한 방법을 사용하여 모델링을 수행하면, 비선형적인 관계를 더 잘 모델링할 수 있으며, 더욱 정확한 예측이 가능하다.

즉,
비선형 회귀식을 완전 제곱식으로 표현하는 방법은 여러가지가 있지만, 가장 대표적인 방법 중 하나는 다음과 같다.
Step 1) 비선형 회귀식을 다음과 같이 변형합니다.
y = b0 + b1f(x)여기서 f(x)는 x에 대한 비선형 함수이다.
Step 2) f(x)를 다음과 같이 완전 제곱식으로 변형합니다.
f(x) = (x - c)^2여기서 c는 x가 가장 크거나 작은 값일 때의 f(x)값을 구하여 그 중간값으로 설정한다.
Step 3) x가 0 이상인 경우, (x - c)^2는 항상 0 이상이다.
따라서 y = b0 + b1(x-c)^2는 x에 대해 비선형이 된다.
하지만 이 방법이 항상 적용 가능한 것은 아니다.
회귀식과 데이터에 따라 다른 방법이 더 적합할 수도 있다!
회귀 계수를 계산하는 방법
-
통계적 방법
통계적 방법은 주로 최소자승법(OLS, Ordinary Least Squares)을 사용합니다.
OLS는 예측값과 실제값의 차이인 잔차(residual)를 최소화하는 방법입니다.
회귀식에서 각 독립 변수의 계수는 이 방법으로 계산됩니다.
이 방법은 계산이 간단하고, 추정된 모델의 신뢰도를 측정하기 위해 사용되는 R-squared와 같은 통계 지표를 계산할 수 있습니다. -
머신 러닝(ML) 방법
머신 러닝 방법은 주로 경사 하강법(Gradient Descent)을 사용합니다.
경사 하강법은 임의의 초기값을 설정하고, 잔차의 제곱을 최소화하기 위해 계수를 반복적으로 조정하는 방법입니다.
이 방법은 일반적으로 더 복잡한 모델과 대규모 데이터셋에 사용됩니다.
두 방법 모두 장단점이 있으며, 사용하는 데이터와 문제에 따라 적절한 방법을 선택해야 합니다.

최소 제곱법은 회귀 분석에서 가장 일반적으로 사용되는 방법 중 하나입니다.
이 방법은 회귀선과 실제 데이터 포인트 사이의 거리를 최소화하는 방식으로 회귀선의 계수를 추정하는 방법입니다.
간단하게 말하면, 최소 제곱법은 데이터 포인트들과 회귀선 간의 거리를 계산하고, 이 거리의 합을 최소화하는 회귀선을 찾는 것입니다.
이 거리의 합을 구하기 위해서는 회귀선의 기울기와 y절편을 조절해가며 MSE(평균 제곱 오차)를 계산하고, 이 값이 최소가 되는 회귀선을 찾으면 됩니다.
이 방법은 수학적으로 간단하고 이해하기 쉽기 때문에, 통계학에서 매우 많이 사용되고 있습니다.

여러 값을 넣어 본 뒤 loss(MSE)가 제일 작은 회귀식을 찾는 것은 수학적 최적화 문제입니다. 즉, 최소화하는 값을 찾기 위해서는 모든 가능한 값들을 대입하여 최소값을 찾아야 합니다.
하지만 이 방법은 계산 시간이 매우 오래 걸리기 때문에, 보통은 기울기 하강법 등의 최적화 알고리즘을 사용하여 최소값을 찾습니다.
이러한 최적화 알고리즘은 자동으로 회귀식을 조정하면서 최적의 회귀식을 찾아줍니다.
따라서, 회귀식을 찾기 위해서는 기본적으로 다양한 데이터를 사용하여 실험을 수행하고, 이를 바탕으로 최적화 알고리즘을 사용하여 회귀식을 찾는 것이 일반적입니다.
이를 통해 최적의 회귀식을 쉽게 찾을 수 있습니다.
최적화 알고리즘 종류
1. Bisection Method
1) 임의의 두개의 값을 설정한다
2) 두 값의 y 값을 비교한다
3) y값이 큰 점을 두 점의 가운데 점으로 바꾼다
4) 임의의 두 값의 차이가 작아질 때 까지 1~3을 반복한다
2. Gradient Descent (경사 하강법)
함수의 기울기(경사)를 구하고 경사의 절댓값이 낮은 쪽으로 계속 이동시켜
극값에 이를 때까지 반복시키는 것
수식
θ = θ - α ∇J(θ)1) 임의의 값 하나를 설정한다
2) 임의의 값에서의 기울기를 계산한다
3) 기울기와 Learning rate를 곱한 값을 임의의 값에서 뺀다
4) 기울기가 0에 가까워질 때 까지 1~3을 반복한다
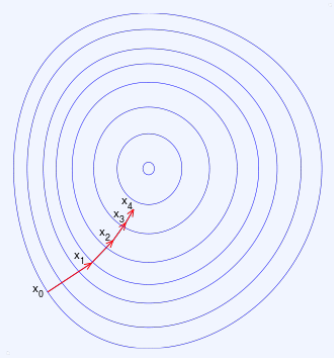
여기서 θ는 최적화하려는 파라미터 벡터, α는 학습률(learning rate)이며, ∇J(θ)는 J(θ)의 기울기 벡터입니다.
학습률은 한 번의 경사 하강법 단계에서 이동할 크기를 결정하는 하이퍼파라미터입니다.
즉, 학습률이 클수록 빠르게 이동하지만 최적점을 지나쳐 버릴 수 있고, 학습률이 작을수록 느리게 이동하지만 정확한 최적점에 더 가깝게 이동할 수 있습니다.
경사 하강법의 목적은 비용 함수 J(θ)를 최소화하는 것입니다.
즉, 경사 하강법을 반복적으로 수행하여 비용 함수가 최소값이 되도록 하는 최적의 파라미터 벡터 θ를 찾습니다.
이를 위해서는 학습률이 적절하게 조절되어야 하며, 비용 함수가 최소값에 수렴할 때까지 경사 하강법을 계속 반복해야 합니다.
