정규화(Regularization)
머신 러닝과 통계에서 모델이 학습 데이터에 과적합(overfitting)되는 것을 방지하는 기술입니다.
과적합은 모델이 너무 복잡하게 되어 학습 데이터의 잡음까지 학습하게 되어, 새로운 데이터에서 성능이 저하되는 문제가 발생합니다.
정규화는 모델이 최적화하려는 목적 함수에 패널티 항을 추가하는 것으로 이루어집니다.
패널티 항은 모델 파라미터의 큰 값을 사용하는 것에 대한 비용을 추가하여, 모델이 작은 파라미터 값을 사용하도록 유도하고 모델을 단순화합니다. L1, L2, 엘라스틱 넷(Elastic Net), 드롭아웃(Dropout) 등 여러 종류의 정규화 기술이 있습니다.
L1 정규화(라소 정규화)는 파라미터의 절대값에 비례하는 패널티를 추가하여,
희소한 해결책(즉, 많은 0 값을 가지는 파라미터)을 사용하도록 모델을 유도합니다.
L2 정규화(릿지 정규화)는 파라미터의 제곱에 비례하는 패널티를 추가하여,
작은 파라미터 값을 사용하도록 모델을 유도합니다.
엘라스틱 넷은 L1과 L2 정규화를 조합하여 희소성과 부드러움 사이의 균형을 제공합니다.
드롭아웃은 일부 뉴런을 무작위로 제거하여 모델이 어떤 특성에 지나치게 의존하지 않도록 합니다.
정규화는 모델이 파라미터 값이 너무 큰 것을 비용으로 추가하여,
모델이 작은 파라미터 값을 사용하고 단순해지도록 유도하여 과적합을 방지하는 데 도움을 줍니다.
Overfitting을 방지하는 법
- 더 많은 학습 데이터
- 모델의 정규화(L1, L2, Elastic Net, Dropout 등 다양한 기법으로 구현될 수 있다)
모델의 정규화
: 모델에 제한을 주어 학습 데이터의 패턴을 모두 외우는 것을 방지하는 방법
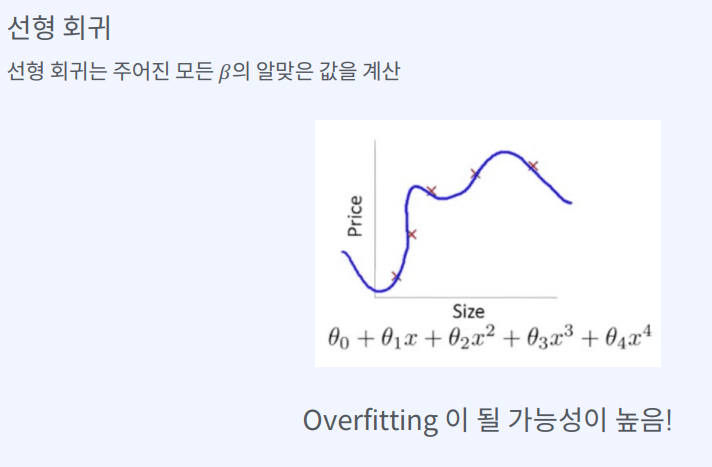
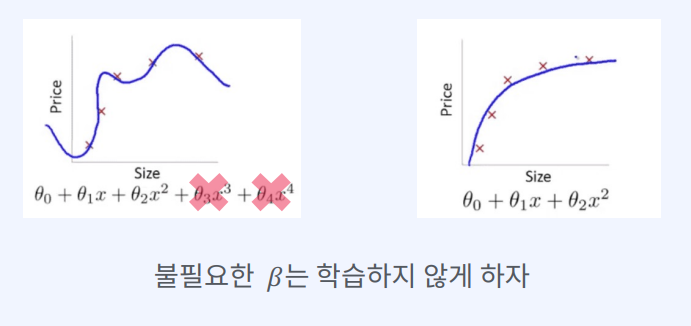
선형 회귀의 목표 : 실제 값을 잘 예측하는 것 (Loss 의 최소화)
선형 회귀의 목표는 입력 변수와 출력 변수 사이의 선형 관계를 모델링하여, 주어진 입력 값에 대한 출력 값을 예측하는 것입니다.
이를 위해 모델은 주어진 학습 데이터를 사용하여 입력 변수와 출력 변수 간의 관계를 학습하고, 새로운 입력 값이 주어졌을 때 출력 값을 예측할 수 있도록 해야 합니다.
선형 회귀 모델은 학습 데이터에 적합한 최적의 선형 함수를 찾는 것이 목표이며,
이때 손실 함수(loss function)를 최소화하는 것이 중요합니다.
일반적으로 선형 회귀 모델에서는 평균 제곱 오차(MSE)를 사용하여 손실 함수를 정의하며,
이를 최소화하는 가중치와 편향 값을 찾는 것이 목표입니다.
따라서 선형 회귀의 목표는 입력 변수와 출력 변수 간의 관계를 잘 모델링하여, 주어진 입력 값에 대한 출력 값을 잘 예측하고, 이를 위해 손실 함수를 최소화하는 최적의 모델 파라미터 값을 찾는 것입니다.

선형 회귀 + 정규화의 목표


선형 회귀와 정규화를 함께 사용하는 경우, 모델의 목표는 입력 변수와 출력 변수 간의 선형 관계를 모델링하는 동시에, 모델의 복잡성을 제어하여 overfitting을 방지하는 것입니다.
이를 위해 모델의 손실 함수(loss function)는 일반적으로 최소제곱 오차(MSE)에 정규화 항을 추가한 형태로 정의됩니다.
L1, L2 정규화 중 어떤 것을 사용할지는 사용자의 선택에 따라 달라질 수 있습니다.
L1 정규화는 가중치 벡터의 절대값(norm)에 비례하는 항을 추가하여 모델의 가중치 값을 0에 가깝게 만들어 sparse한 모델을 만들어주는 역할을 합니다.
L2 정규화는 가중치 벡터의 제곱(norm)에 비례하는 항을 추가하여 모델의 가중치 값을 작게 만들어주는 역할을 합니다.
따라서 선형 회귀 + 정규화의 목표는 입력 변수와 출력 변수 간의 선형 관계를 잘 모델링하면서, 모델의 복잡성을 제어하여 일반화 성능을 향상시키는 것입니다.
이를 위해 손실 함수를 최소화하는 최적의 가중치 값을 찾는 것이 중요하며, 이때 L1 또는 L2 정규화 항을 추가하여 가중치 값을 제한합니다.
선형 회귀 + 정규화의 종류
선형 회귀에 L1 또는 L2 정규화를 적용한 것을 LASSO와 Ridge라고 합니다.
-
LASSO (Least Absolute Shrinkage and Selection Operator)는 L1 정규화를 사용하여 모델의 가중치를 0에 가깝게 만들어 sparse한 모델을 만드는 방식
-
Ridge는 L2 정규화를 사용하여 모델의 가중치를 작게 만드는 방식

