[딥러닝] Optimizer

M Hardt, Train faster, generalize better: Stability of stochastic gradient descent, 2016
Adaptive methods (Adam, RMSprop) is worse to generalize than non-adaptive methods(SGD, Momentum).

• 가정
  • 이미지: 256장
  • epoch: 10
  • batch size: 8

1. None

• 모든 이미지(256장)로 gradients를 한 번 계산하고 update
• 한 epoch에서 위 update를 1번만 함
• 학습이 종료될 때까지 총 10번의 update를 반복

2. SGD (Stochastic Gradient Descent)

• 랜덤하게 선택된 1장의 이미지로 gradients를 한 번 계산하고 update
• 한 epoch에서 위 update를 256번(총 이미지 개수) 반복
• 학습이 종료될 때까지 총 2560번의 update를 반복

3. Mini-batch SGD

• 랜덤하게 선택된 8장의 이미지로 gradients를 한 번 계산하고 update
• 한 epoch에서 위 update를 32번($={총\,이미지\,개수 \over batch\,size}$) 반복
• 학습이 종료될 떄까지 총 320번의 update를 반복

4. Momentum

• 수식
  $v_{dW} = \beta v_{dW} + (1 - \beta) dW \\ \, \\ W = W - \alpha v_{dW}$
• Compute an exponentially weighted average of the gradients and update the weights with that value
• 위 그림에서 최적의 gradients를 찾기 위해서는 첫 시작점에서 목표값까지는 수직보다는 수평 방향(우측 →)으로 움직여야 한다.
  • 파란색 선은 momentum을 적용하지 않은 방법이다.
  • 빨간색 선은 momentum을 적용한 방법이다. momentum을 적용했기 때문에 수직 방향의 derivative는 ↑과 ↓이 반복되므로 평균이 0에 가까워진다. 반면, 수평 방향은 derivative가 모두 →를 가리키고 있기 때문에 평균도 →이 된다. 따라서 momentum을 적용하지 않은 파란색 선보다 더욱 빠르게 최적화된다.
• 보통 $\beta = 0.9$로 설정 (지난 10일 간의 온도를 평균하는 것에 비유)
• 간혹 논문 등에서 $(1 - \beta)$를 생략하여 $v_{dL \over dW} = \beta v_{dL \over dW} + {dL \over dW}$로 표현하는 경우가 있다. 이 경우는 $\beta$를 조정하면 learning rate인 $\alpha$도 영향을 받아 $\alpha$를 다시 조정해주어야 하므로 Andrew Ng 교수는 이를 선호하지 않는다.
• PyTorch나 TensorFlow는 default로 위 수식과는 약간 다르게 구현한 것으로 보인다.
  • PyTorch
    
  • TensorFlow
    

5. AdaGrad

6. RMSprop (Root Mean Squared prop)

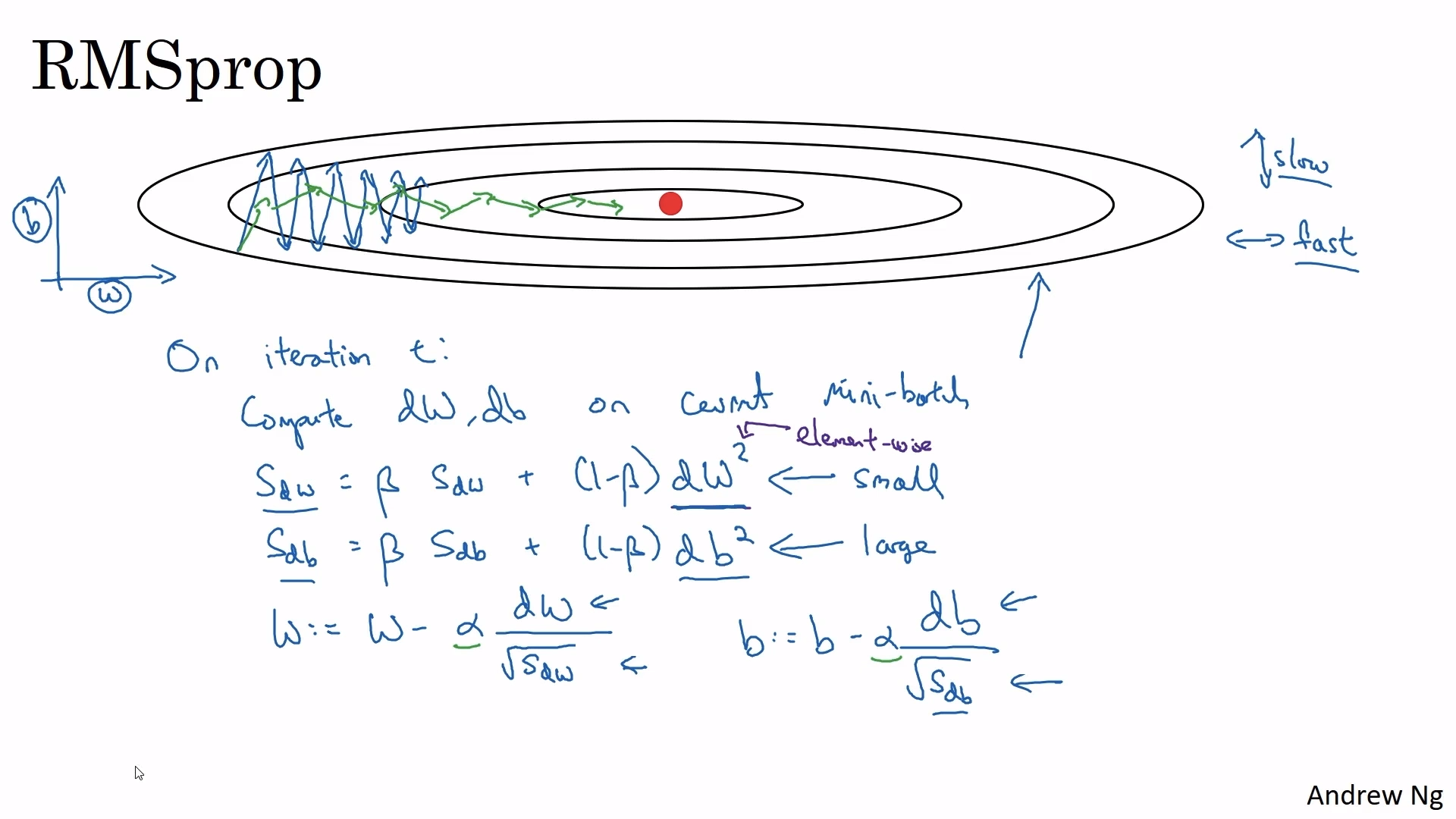
• 수식
  $s_{dW} = \beta s_{dW} + (1 - \beta) (dW)^2 \\ \, \\ W = W - \alpha {dW \over \sqrt{s_{dW}} + \epsilon}$
• 위 그림에서 최적의 gradients를 찾기 위해서는 첫 시작점에서 목표값까지는 수직보다는 수평 방향(우측 →)으로 움직여야 한다.
  • 파란색 선은 RMSprop을 적용하지 않은 방법이다.
  • 초록색 선은 RMSprop을 적용한 방법이다. 수직 방향의 derivative가 수평 방향의 derivative보다 훨씬 크다. 따라서 RMSprop을 적용하면 수식의 분모 때문에 수직 방향의 derivative는 작게 update되고, 수평 방향의 derivative는 크게 update된다.
• 0으로 나누는 것을 방지하기 위해 보통 $\epsilon = 10^{-8}$로 설정하지만 이보다 약간 큰 값도 괜찮다.

7. Adam (Adaptive Moment Estimation)

• Momentum + RMSprop
• 수식
  • Momentum
    $v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW$
  • RMSprop
    $s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) dW^2$
  • Bias correction
    $v_{dW}^{corrected} = {v_{dW} \over 1 - {\beta_1}^t} \\ \, \\ s_{dW}^{corrected} = {s_{dW} \over 1 - {\beta_2}^t}$
  • Update
    $W = W - \alpha {v_{dW}^{corrected} \over \sqrt{s_{dW}^{corrected}} + \epsilon}$
• Hyperparameters
  보통 $\alpha$를 찾으며, 나머지는 default를 사용한다.
  • $\alpha:$ needs to be tune
  • $\beta_1: 0.9$
  • $\beta_2: 0.999$
  • $\epsilon: 10^{-8}$ (doesn't affect performance much at all)

---

📙 참고

• Andrew Ng - Mini Batch Gradient Descent (C2W2L01)
• Andrew Ng - Gradient Descent With Momentum (C2W2L06)
• Andrew Ng - RMSProp (C2W2L07)
• Andrew Ng - Adam Optimization Algorithm (C2W2L08)