[딥러닝] L2 Regularization

• Overfitting이 의심될 때 가장 먼저 시도할 것

1. L2&L1 regularization

• L2 regularization

  $w: (n^{[l-1]}, n^{[l]}) \\ \, \\ J(w^{[1]}, ..., w^{[L]}) = {1 \over m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + {\lambda \over 2m} \sum_{l=1}^L {\lVert w^{[l]} \rVert}_F^2 \\ \, \\ {\lVert w^{[l]} \rVert}_F^2 = \sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}} (w_{ij}^{[l]})^2$

• L1 regularization

  $J(w^{[1]}, ..., w^{[L]}) = {1 \over m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) + {\lambda \over 2m} \sum_{l=1}^L {\lVert w^{[l]} \rVert}_1 \\ \, \\ {\lVert w^{[l]} \rVert}_1 = \sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}} \left\vert w_{ij}^{[l]} \right\vert$

  $w$ will be sparse, which means there are many 0s in the $w$ vector. Some people say this can help with compressing the model. Because the certain parameters are 0, then we need less memory to store the model. But Andrew Ng doesn't think this helps much at all.

• $\lambda$: hyperparameter, 각 층마다 다른 값을 적용해도 된다.

2. Backpropagation (Why Weight decay?)

• 기존

  $dW^{[l]} = (from \,\, backprop) \\ \, \\ W^{[l]} = W^{[l]} - \alpha dW^{[l]} \\ \, \\ W^{[l]} = W^{[l]} - \alpha (from \,\, backprop)$

• regularization

  $dW^{[l]} = (from \,\, backprop) + {\lambda \over m} W^{[l]} \\ \, \\ W^{[l]} = W^{[l]} - \alpha dW^{[l]} \\ \, \\ = W^{[l]} - \alpha [(from \,\, backprop) + {\lambda \over m} W^{[l]}] \\ \, \\ = W^{[l]} - {\alpha \lambda \over m} W^{[l]} - \alpha (from \,\, backprop) \\ \, \\ = (1 - {\alpha \lambda \over m}) W^{[l]} - \alpha (from \,\, backprop) \\$

  $(1 - {\alpha \lambda \over m}) \le 1$이기 때문에, l2 regularization은 Weight Decay라고 불린다.

3. Regularization이 Overfitting을 해결할 수 있는 이유

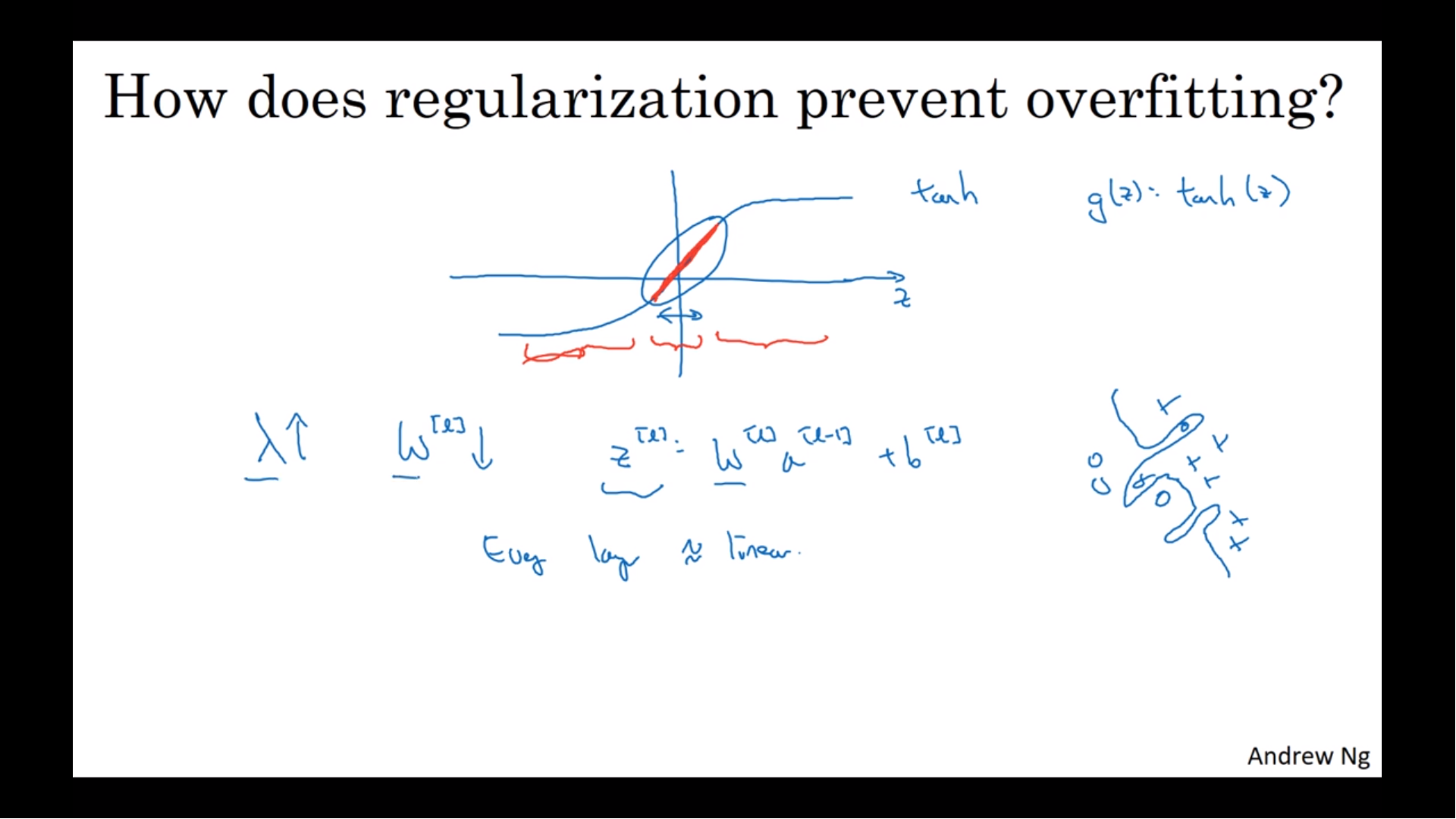
activation function이 tanh일 때를 살펴보자. $\lambda$가 커지면 $W^{[l]}$은 작아지기 때문에 $z^{[l]}$도 작아진다. 작은 $z$값은 tanh에서 선형적인 부분만을 사용한다. 따라서 신경망은 복잡한 비선형적인 구조보다는 비교적 간단한 선형적인 구조를 가지게 된다.

4. 기타 regularization 방법

• Dropout [zzwon1212 - Dropout]
• Data augmentation [Andrew Ng - Other Regularization Methods (C2W1L08)]
• Early stopping [Andrew Ng - Other Regularization Methods (C2W1L08)]
  • L2 regularization은 hyperparameter인 $\lambda$를 찾기 위해 학습을 여러 번(여러 번의 epoch * 여러 번) 해야 하지만, early stopping은 한 번의 학습(여러 번의 epoch * 1번)만 하면 된다. 그러나 cost function을 optimize하는 것과 overfitting을 prevent하는 것 사이의 orthogonalization 문제에서 자유롭지 못하다. 많은 사람들이 early stopping을 사용하지만, Andrew Ng은 컴퓨팅 파워가 충분하다면 L2 regularization의 $\lambda$를 찾는 것을 더 선호한다.
• Batch Normalization [zzwon1212- Batch Normalization]

5. PyTorch 적용

• torch.optim.SGD()의 weight_decay를 설정

---

📙 참고

• Andrew Ng - Regularization (C2W1L04)
• Andrew Ng - Why Regularization Reduces Overfitting (C2W1L05)