Transformer for Image - 시각적 이해를 위한 머신러닝 5

zzwon1212·2024년 7월 16일

딥러닝

목록 보기

29/33

14. Transformers Ⅱ

14.1. Transformer-based Image Models

14.1.1. ViT (Vision Transformers)

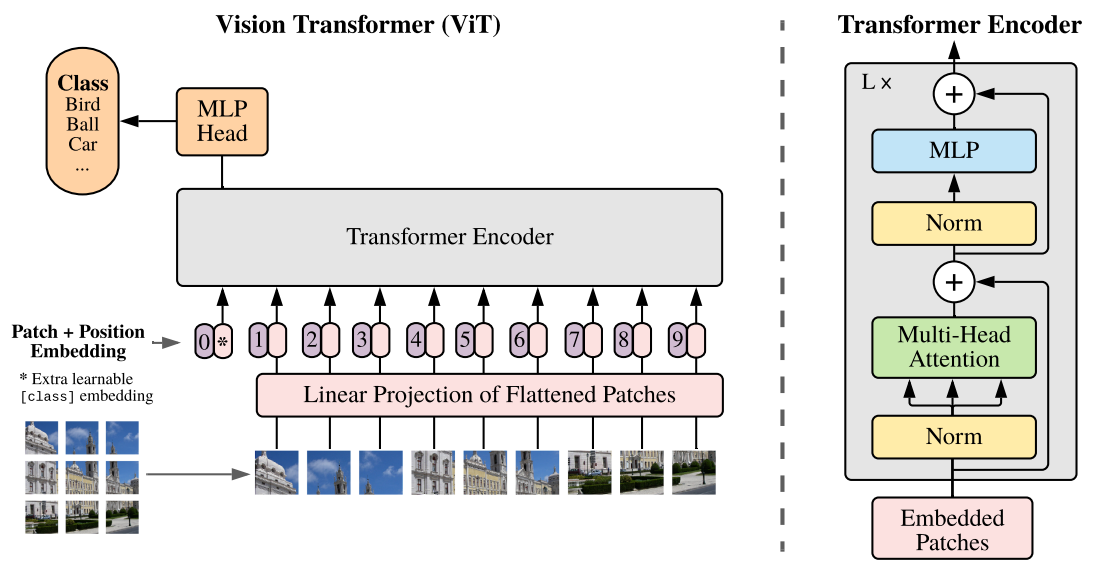
The standard Transformer model is directly applied to images
- An image is split into $16 \times 16$ patches. Each token is the patch instead of a word.
- The sequence of linear embeddings of these patches are fed into the Transformer.
- Eventually, an MLP is added on top of the [CLS] token to classify the input image.
Shape and Architecture
- image $\mathrm{x} \in \mathbb{R}^{H \times W \times C}$
- sequence of flattend 2D patches
  $\mathrm{x}_p \in \mathbb{R}^{N \times (P^2 \cdot C)}$
  - $P$ is the resolution of image patch.
  - $N = HW / P^2$
- patch embedding
  $\mathrm{x_{class}}, \mathrm{x}_p^1 \mathbf{E},\mathrm{x}_p^2 \mathbf{E}, ..., \mathrm{x}_p^N \mathbf{E} \in \mathbb{R}^{D}$
  - trainable linear projection $\mathbf{E} \in \mathbb{R}^{(P^2 \cdot C) \times D}$
- positional embdding $\mathbf{E}_{pos} \in \mathbb{R}^{(N+1) \times D}$
- The MLP contains two layers with a GELU non-linearity.
  - $\mathrm{z}_0 = [\mathrm{x_{class}}; \mathrm{x}_p^1 \mathbf{E};\mathrm{x}_p^2 \mathbf{E}; ...; \mathrm{x}_p^N \mathbf{E}] + \mathbf{E}_{pos}$
  - ${\mathrm{z}'}_l = \mathrm{MSA(LN(z_{\mathit{l}-1}))} + \mathrm{z}_{l-1}$ , $l = 1, ..., L$ (Multi-Head Self-Attention)
  - ${\mathrm{z}}_l = \mathrm{MLP(LN(z'_{\mathit{l}}))} + \mathrm{z'}_{l}$
  - $\mathrm{y} = \mathrm{LN(z_\mathit{L}^0)}$
Experiments and Discussion
- ViT is computationally expensive. It takes 300 days with 8 TPUv3 cores.
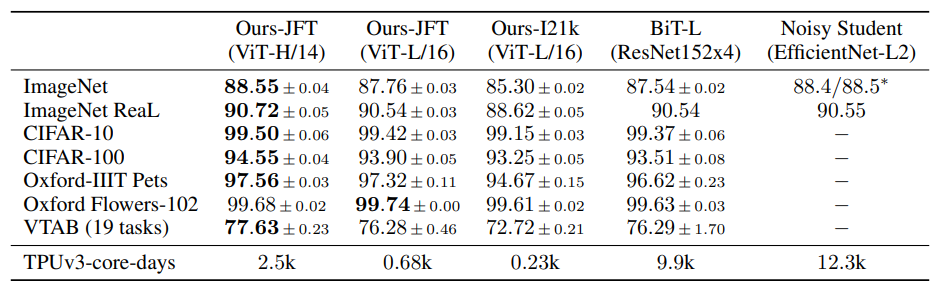
- ViT performs well only when trained on an extremely large dataset. Why?
  - ViT does NOT imply any inductive bias (spatial locality & positional invariance) of CNNs.
  - So it requires large data to learn those purely from the data.
  - However, with sufficient data, it can outperform CNN-based models, since it iis capable of modeling hard cases beyond spatial locality.
- Position embedding
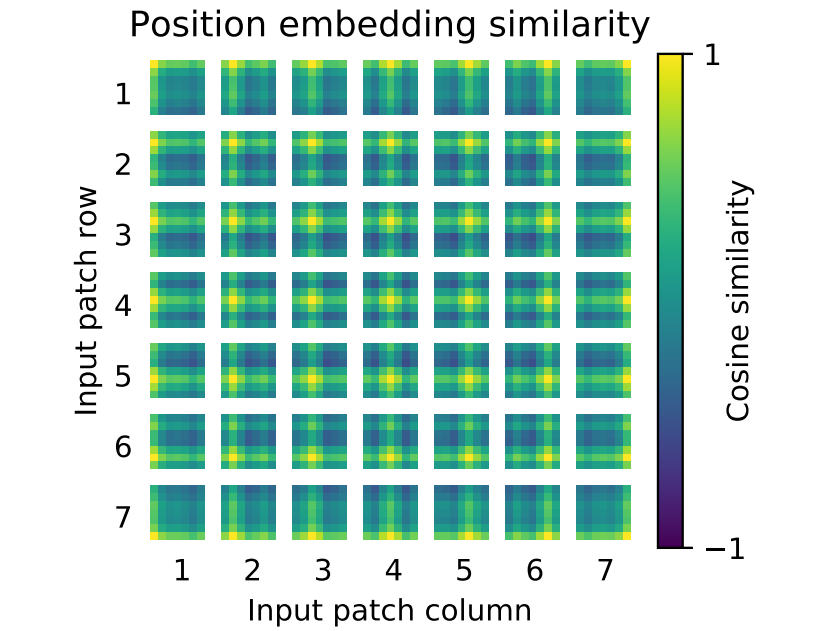
  - Closer patches tend to have more similar position embeddings, automatically learned from data.

14.1.2. DeiT (Data-efficient image Transformers)

Contributions
- ViT does not generalize well when trained on insufficient amounts of data.
  → DeiT uses Imagenet as the sole training set.
- The training of ViT models involved extensive computing resources.
  → DeiT train a vision transformer on a single 8-GPU node in two to three days.
Main idea: Distillation
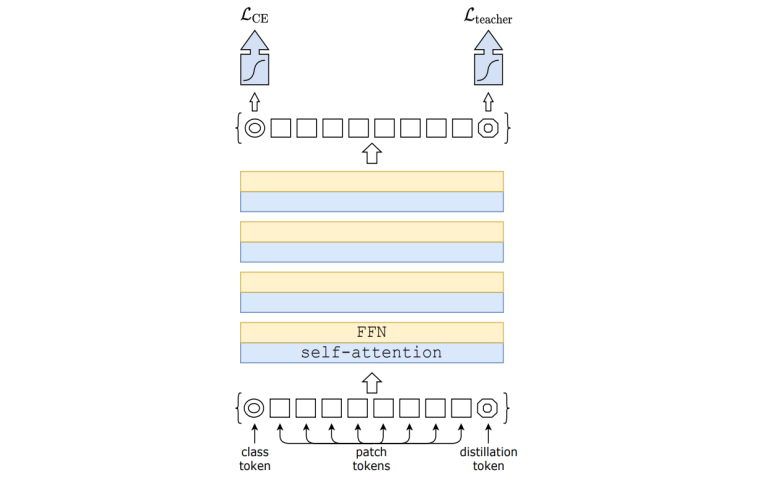
- Teacher model
  DeiT exploits strong image classifier as a teacher model to learn a transformer. DeiT simply includes a new distillation token. The distillation token interacts with the class and patch tokens through the self-attention layers.
- Soft vs. Hard distillation
  - notations
    - $Z_\text{t}$ : teacher logits
    - $Z_\text{s}$ : student logits
    - $\tau$ : temperature for the distillation
    - $\text{KL}$ : the Kullback-Leibler divergence loss
    - $\psi$ : the softmax function
    - $y_t = \text{argmax}_c Z_\text{t}(c)$ : the hard decision of the teacher
  - Soft distillation $\mathcal{L}_{\text{global}} = (1 - \lambda) \mathcal{L}_{\text{CE}} (\psi(Z_s), y) + \lambda \tau^2 \text{KL} (\psi(Z_s / \tau), \psi(Z_t / \tau))$
  - Hard-label distillation $\mathcal{L}_{\text{global}}^{\text{hardDistill}} = \frac{1}{2} \mathcal{L}_{\text{CE}} (\psi(Z_s), y) + \frac{1}{2} \mathcal{L}_{\text{CE}} (\psi(Z_s), y_t)$
- Distillation token
Experiments and Discussion
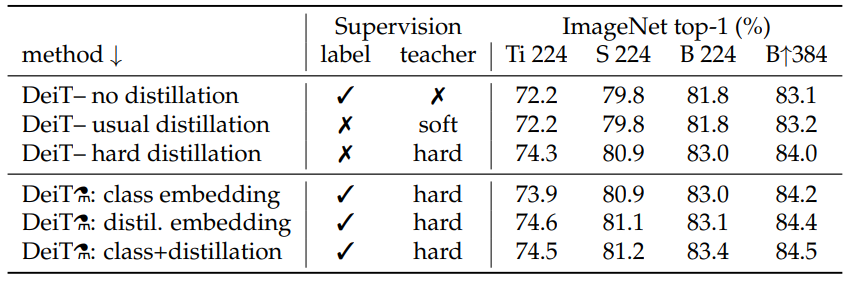
- Hard distillation (83.0%) significantly outperforms soft distillation (81.8%), even when using only a class token.
- The two tokens (class + distillation) is significantly better than the independent classifiers.
- The distillation token gives slightly better results than the class token probably due to the inductive bias of convnets.

14.1.3. Swin Transformer

Issues with Vanilla ViT Model
- Too much computational cost due to lack of inductive bias
  - The model need to refer to all tokens in the image, even though in most cases only the nearby patches are informative.
- Fixed-size patches
  - Variations in the scale of visual entities are not properly modeled.
  - Pixels across patches cannot directly interact even though they are adjacent.
Main idea
- Inductive Bias Reintroduced (by Self-attention in non-overlapped windows)
  For efficient modeling, the model compute self-attention within local windows. The number of patches in each window is fixed.
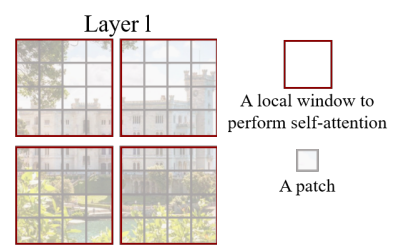
  - Time Complexity
- Hierarchical Structure
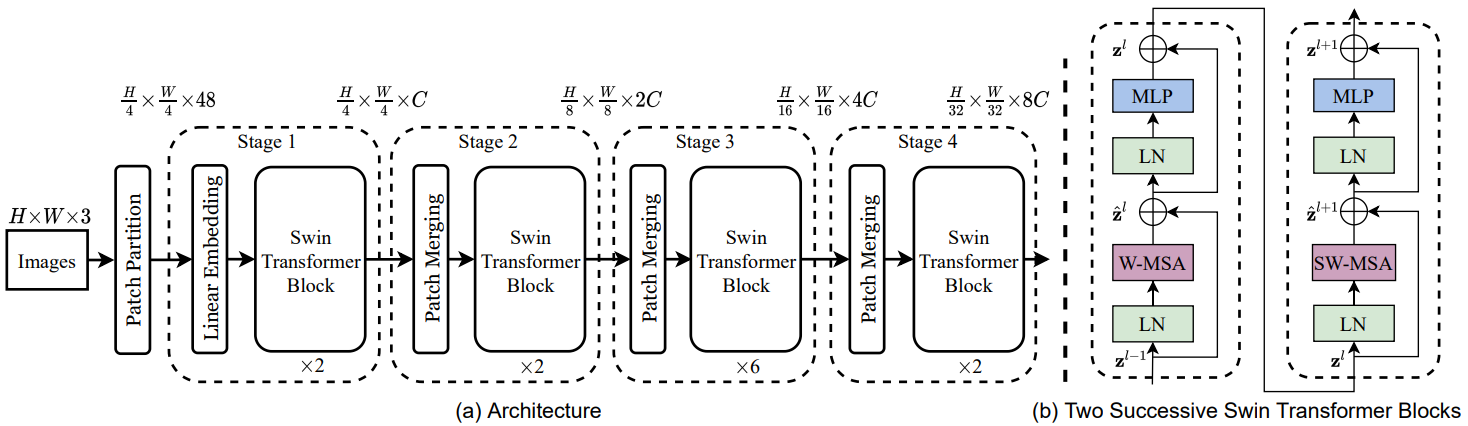
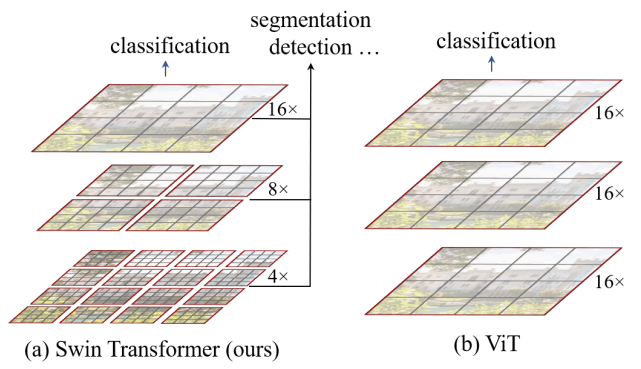
  The model constructs a hierarchical representation by starting from small-sized patches in deeper Transformer layers. To produce a hierarchical representation, the number of tokens is reduced by patch merging layers as the network gets deeper. It can serve as a general-purpose backbone for both image classification and dense recognition tasks.
- Shifted Window (Swin) Partitioning
  A key design element is shift of the window partition between consecutive self-attention layers. The shifted windows bridge the windows of the preceding layer, providing connections among them that significantly enhance modeling power.
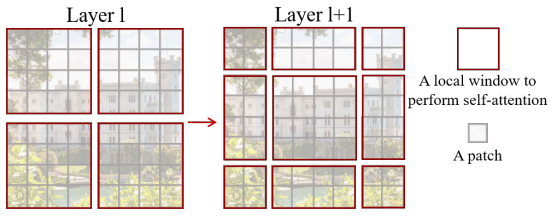
- Relative Position Bias
  Since only the patches within the window participate in self-attention, only the relative position bias within the window does matter.

14.1.4. CvT (Convolutional vision Transformers)

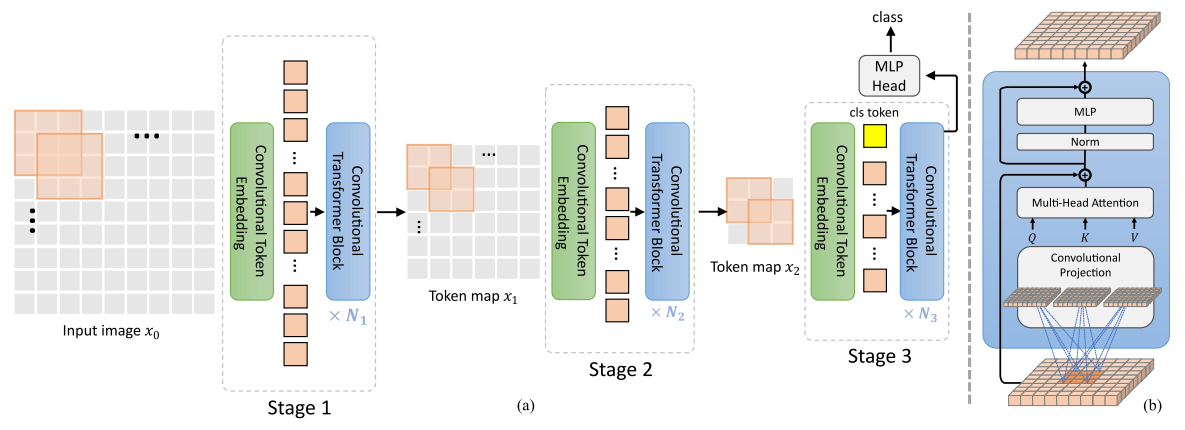
A multi-stage (3 in this work) hierarchy design borrowed from CNNs is employed. Each stage has two parts, Convolutional Token Embedding and Convolutional projection.

Issues with Vanilla ViT Model
- Too much computational cost due to lack of inductive bias
  - The model need to refer to all tokens in the image, even though in most cases only the nearby patches are informative.
- Fixed-size patches
  - Variations in the scale of visual entities are not properly modeled.
  - Pixels across patches cannot directly interact even though they are adjacent.
Main idea
- Convolutional Token Embedding layer
  - The layer is implemented as a convolution with overlapping patches with tokens reshaped to the 2D spatial grid as the input.
  - The degree of overlap can be controlled via the stride length.
  - These layers have the ability to represent increasingly complex visual patterns over increasingly larger spatial footprints, simliar to CNNs. Since
    - each stage progressively reduce the number of tokens (i.e. feature resolution), thus achieving spatial downsampling.
    - each stage progressively increase the width of the tokens (i.e. feature dimension), thus achieving increased richness of representation.
  - Implementation
    - Input to stage $i$
      $x_{i-1} \in \mathbb{R}^{H_{i-1} \times W_{i-1} \times C_{i-1}}$
      - 2D image or 2D-reshaped output token map form a previous stage
    - new tokens
      $f(x_{i-1})$
      - where $f(\cdot)$ is 2D conv operation
      - channel size: $C_i$
      - kernel size: $s \times s$
      - stride: $s - o$
      - padding: p
    - The new token map
      $f(x_{i-1}) \in \mathbb{R}^{H_i \times W_i \times C_i}$
      - height and width $H_i = \lfloor \frac{H_{i-1} + 2p - s}{s - o} + 1 \rfloor, W_i = \lfloor \frac{W_{i-1} + 2p - s}{s - o} + 1 \rfloor$
      - is then flattened into size $H_i W_i \times C_i$
- Convolutional projection
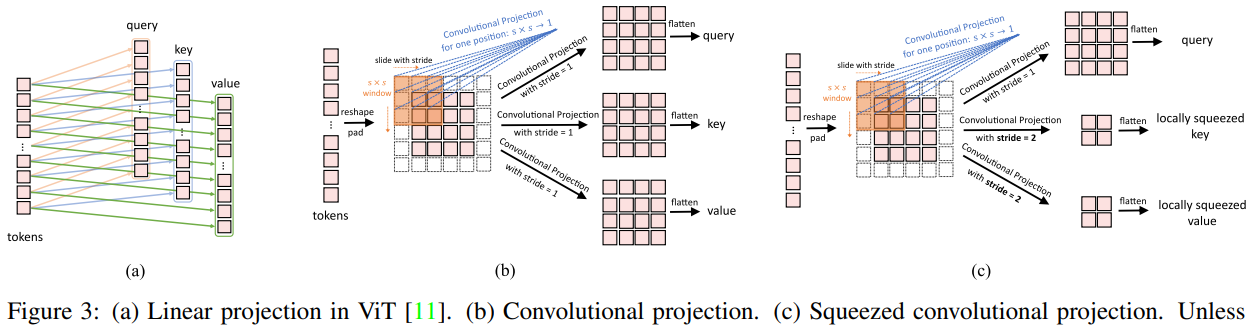
  - Next, a stack of the proposed Convolutional Transformer Blocks comprise the remainder of each stage.
  - A depth-wise separable convolution operation, referred as Convolutional Projection, is applied for query, key, and value embeddings respectively, instead of the standard position-wise linear projection in ViT.
  - $s \times s$ Convolutional Projcection
    $x_i^{q / k /v} = \text{Flatten}(\text{Conv2d}(\text{Reshape2D}(x_i), s)).$
    - $\text{Conv2d}$ is a depth-wise separable convolution implemented by: $\text{Depth-wise Conv2d → BatchNorm2d → Point-wise Conv2d}$

14.2. Transformer-based Video Models

14.2.1. ViViT (Video Vision Transformer)

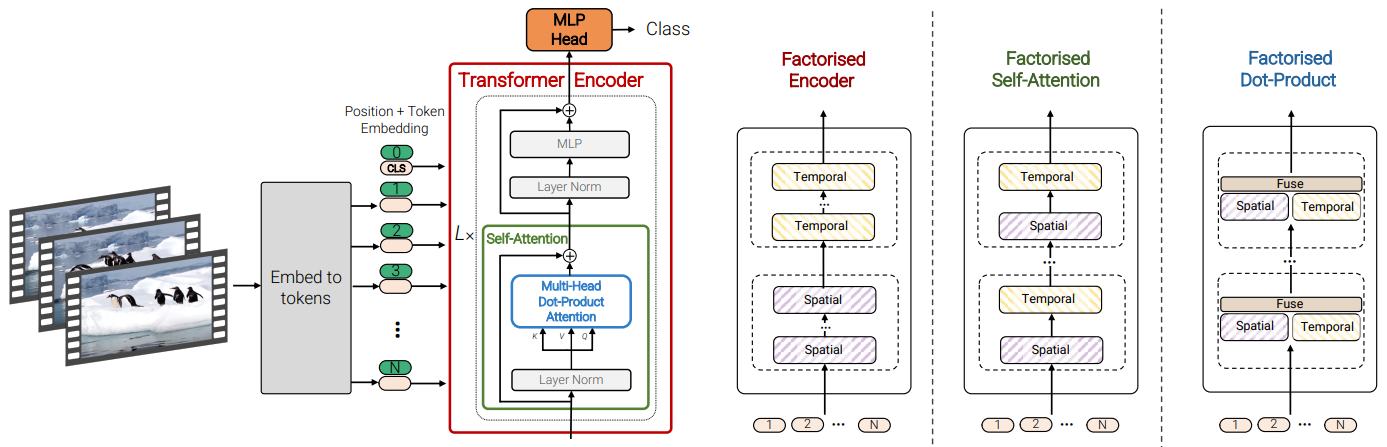
Model 1: Spatio-temporal attention
- Naturally extending the idea of ViT to video classification task
- Total $n_h \times n_w \times n_t$ patches are fed into the Transformer Encoder.
- Computationally expensive: $O(n_h^2 n_w^2 n_t^2)$
  - Basic ideas to reduce computational overhead
Model 2: Factorized encoder
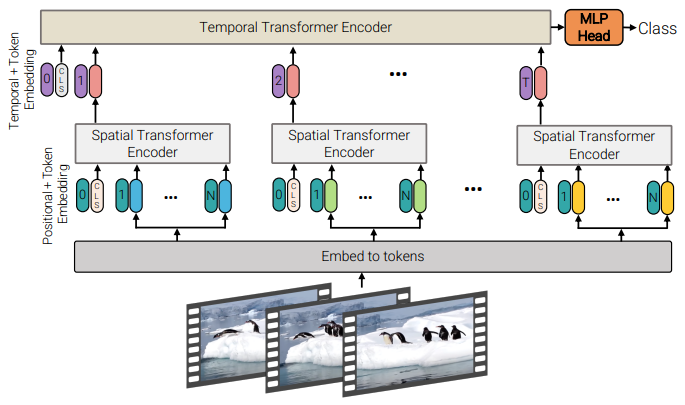
- First, Spatial Transformer Encoder (=ViT)
- Then, each frame is encoded to a single embedding and fed into the Temporal Transformer Encoder
- Complexity: $O(n_h^2 n_w^2 + n_t^2)$
Model 3: Factorized self-attention
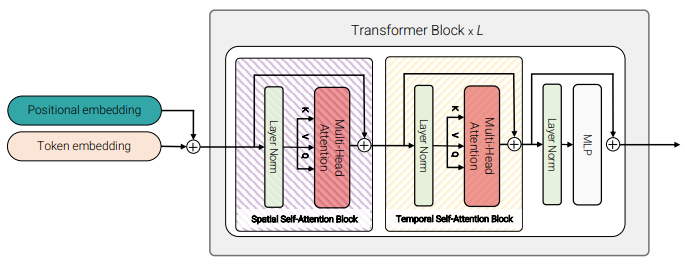
- First, only compute self-attention spatilally (among all tokens, extracted from the same temporal index)
- Then, temporally (among all tokens extracted from the same spatial index)
- No [CLS] is used to avoid ambiguities.
Model 4: Factorized dot-product attention
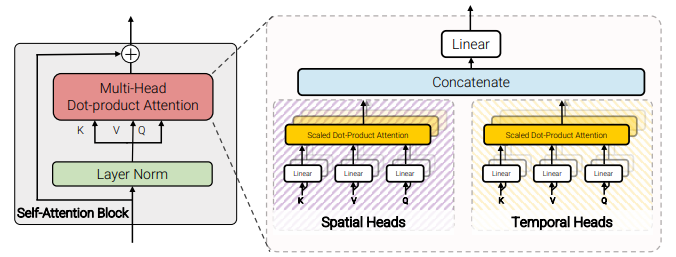
- Recall that the Transformer is based on Multi-head attentions.
- Half of the attention heads operate with keys and values from same spatial indices.
- The other half operate with keys and values from same temporal indices.
Experiments and Discussion
- Dataset sparsity problem
  - ViT requires extremely large dataset.
  - There's no large video dataset.
  - Model 2 can be initialized with ViT.
- Comparing Model 1, 2, 3, 4
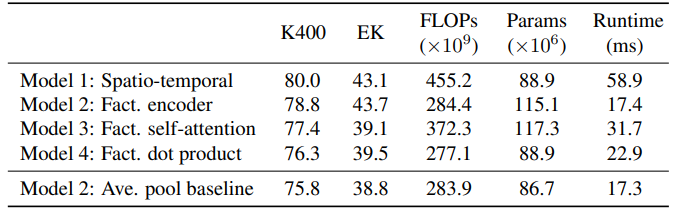
  - The naive model (Model 1) performs the best, but most expensive.
  - Model 2 is the most efficient.

14.2.2. TimeSFormer

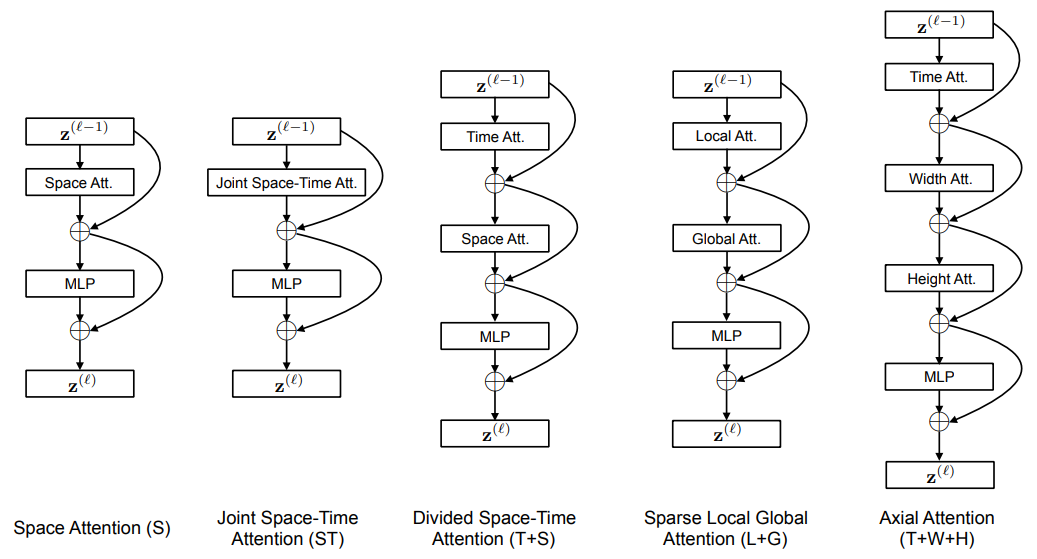
(S) = ViT
(ST) = ViViT Model 1
(T+S) $\approx$ ViViT Model 3

14.2.3. MViT (Multiscale Vision Transformers)

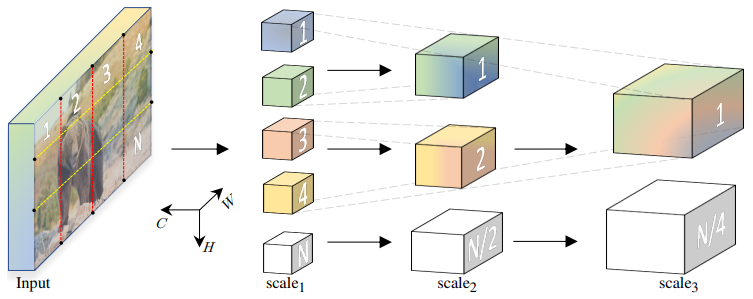
A similar idea to CvT, applied to videos.
Multi Head Pooling Attention (MHPA)
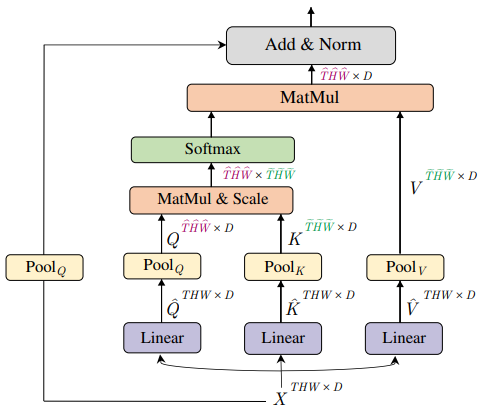
- Progressively pooling the resolution from input to output of the network, while expanding the channel capacity, following the widely-used paradigm with CNNs.
- Pooling layers reduce Time-Height-Width resolutions.
- Queires and keys/values are reduced to different sizes, similar principle to the squeezed convolutional projection in CvT.
Compared to CvT
- cube $_1$ corresponds to the first Conv Token Embedding layer.
- After then, MViT shrinks the feature map size by pooling operations within MHPA, not conv operations as in CvT.
- Recall that Conv Transformer Block in CvT self-contains MLP layers. This block is analogous to [MPHA; MLP] in MViT.
Discussion
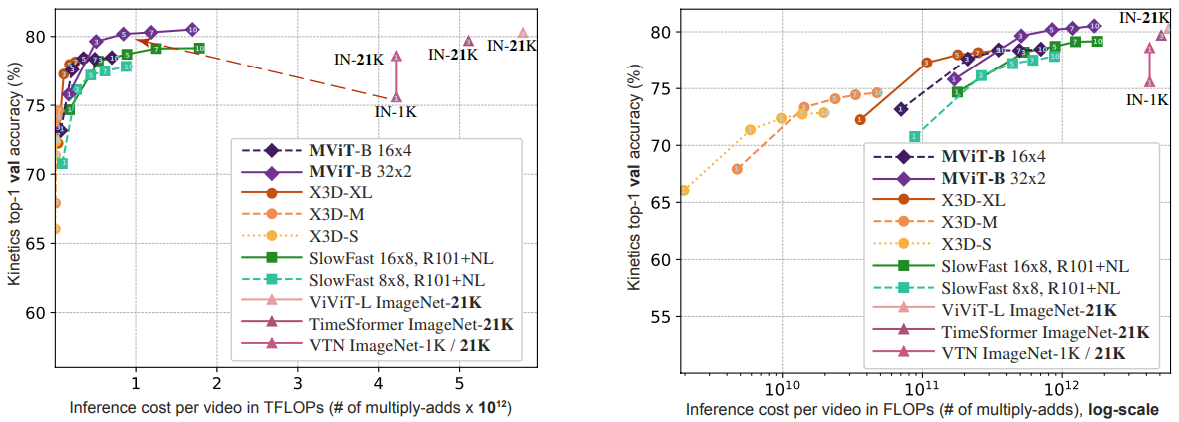
- Achieves slightly better performance than ViViT and TimeSformer, with significantly smaller inference cost.
- Comparing with CNN models:
  - X3D model
  - SlowFast model