Point Cloud 의 Surface Roughness 를 구하기

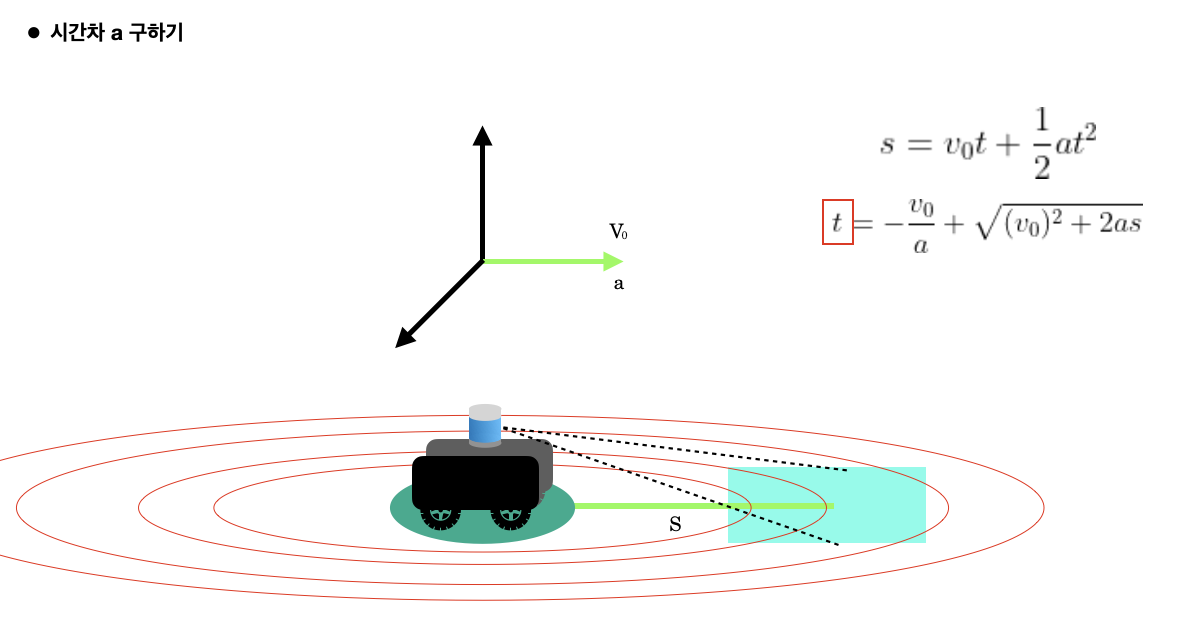
Point Cloud 형태와 IMU 데이터의 상관관계를 알기 위한 1차 시도

Point Cloud 와 IMU 데이터

Point Cloud 를 분석하면 지표면의 울퉁불퉁한 정도 (Bumpiness) 를 알 수 있다. 이 Bumpiness 를 어떻게 정의할 것이고, 이 요소가 주행에 어떤 영향을 미치는지 알아보자.

목표 : Surface Roughness 로부터 예측된 IMU 데이터값을 기반으로 Point Cloud 를 단계별로 분류하기

이때 Ground Truth 는 IMU 데이터값으로부터 얻을 수 있으므로 , 이 두 데이터간의 상관관계를 분석한다면 Point Cloud 만 있어도 IMU 값을 예측할 수 있을 것이라고 생각했다.

획득 시점 차이

우선 IMU 데이터값과 Point Cloud 분포에 따른 상관관계를 알기 위해서는 '획득 시점 차이' 라는 문제를 해결해야 했다.

예를 들어,

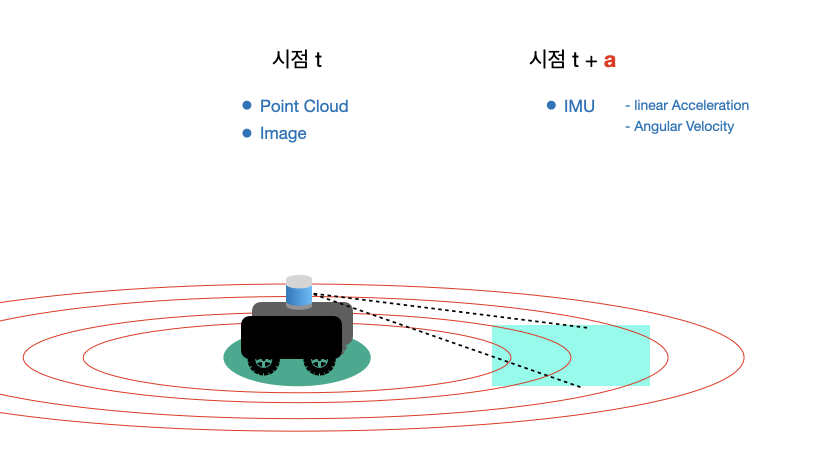
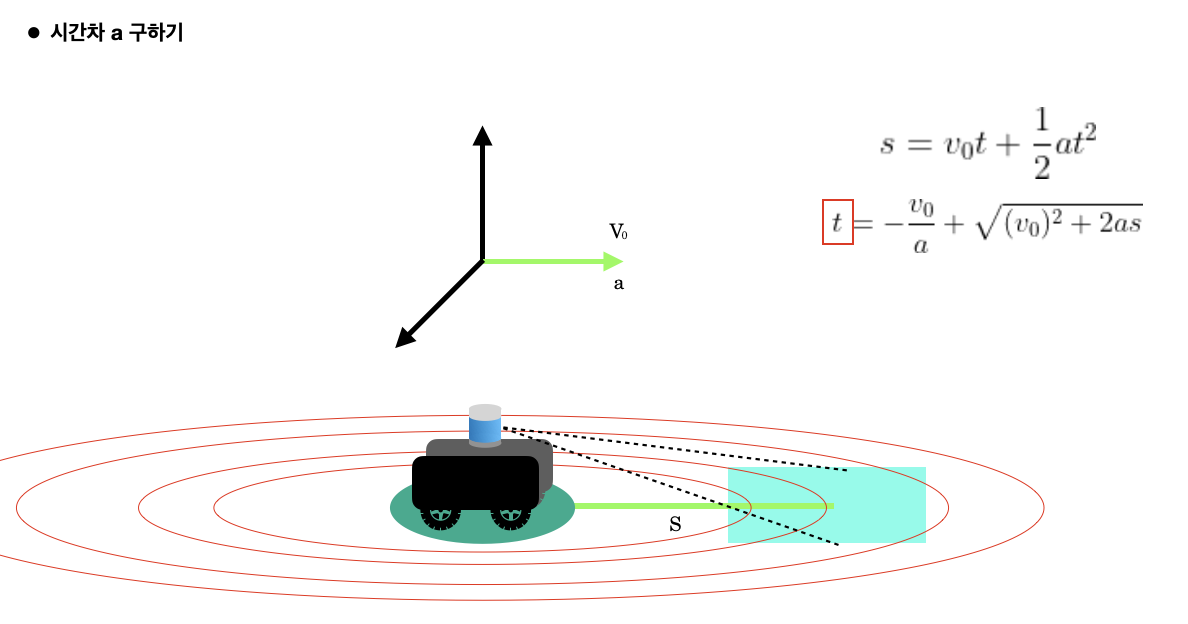
다음과 같이 시점 t 에서 imu 는 로봇이 위치한 영역에 대한 데이터를 획득하지만, LiDAR 와 Camera 는 '앞에 보이는 영역' 에 대한 데이터를 획득한다.
따라서 특정 영역에 대해서 PC 데이터와 그에 해당하는 IMU 데이터를 얻기 위해서는 시점 차이 (a) 를 계산해야 한다고 생각했다.

IMU 데이터를 이용하면 Linear Acceleration, Angular Velocity 값을 얻을 수 있으므로 이를 이용해서 a 값을 추정했다.

획득 시점에 따라 데이터셋 저장하기

사용 데이터셋 : RELLIS-3D Dataset

나는 이 문제를 DNN 으로 해결하고 싶었기 때문에 다음 데이터들을 세트로 저장했다.

1. t 시점의 Point Cloud
2. t 시점의 image
3. t+a 시점의 IMU 데이터

이때 Point Cloud 는 모바일 로봇 크기만큼 잘랐고, IMU 속도 데이터에서 추산한 시점 차이에 대한 오차를 줄이고자 로봇 바로 앞의 PC 데이터를 사용했다. 사진도 PC 와 동일한 영역을 가리키도록 잘라서 저장했다.

Surface Roughness

DNN 모델을 구성하기 위해서 Point Cloud 에서 Feature 을 뽑아내 수치화할 필요가 있다고 생각했다.
Point Cloud 에서 사용할 수 있는 수치들은 다음과 같다.

• Normal Vector
• Intensity
• Moment Of Inertia
• Curvature
• Surface Area
• Bag of words
  ...

이 중 Normal Vector 와 Intensity 를 사용하였다.

순서

1. Normal Vector 구하기
2. 중심점으로부터 현재 점으로의 벡터 구하기
3. Covariance Matrix 의 Eigen Value, Eigen Vector 구하기
4. PC 중심과 점까지의 벡터와 EigenVector 내적하기
5. 이들의 평균 구하기

원리 Concept

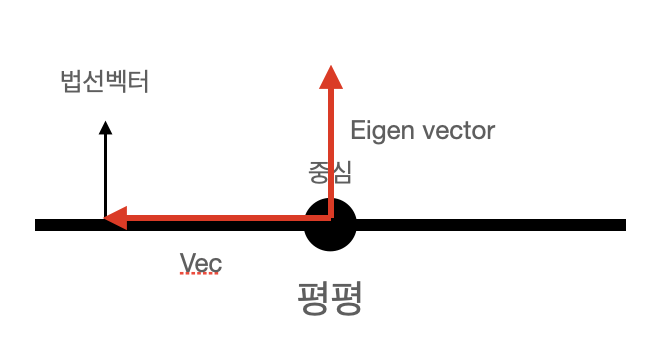
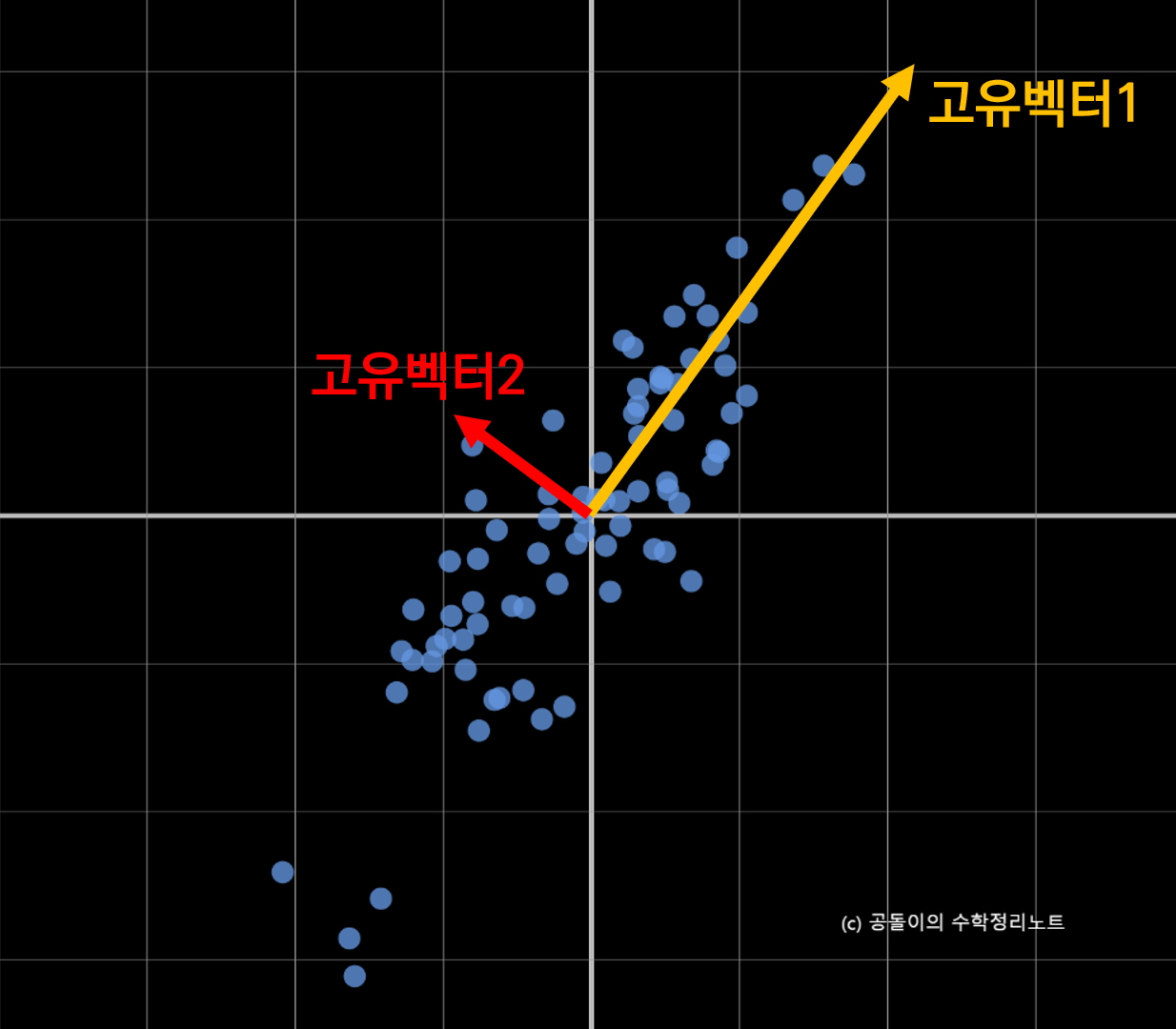
(출처 : 공돌이의 수학정리노트)

공분산 행렬의 고유 벡터는 데이터가 어느 방향으로 분산되어 있는지를 나타내 준다.
만약 포인트 클라우드가 평평하게 분포하고 있을 경우, Eigen Vector 의 방향은 "데이터가 덜 분포하는 방향' 을 향하기 때문에 사진에 표시된 것 처럼 수직하게 형성될 가능성이 높다.
이때 vec 이 데이터 분포의 중심으로부터 점까지의 벡터이고,
pc가 평평할 수록 이 둘의 내적값이 0에 가까우므로 Pseudo Code 에 따라 구한 roughness 값은 pc 의 분포가 평평하지 않을 수록 클 것이다.

1. Normal Vector 구하기

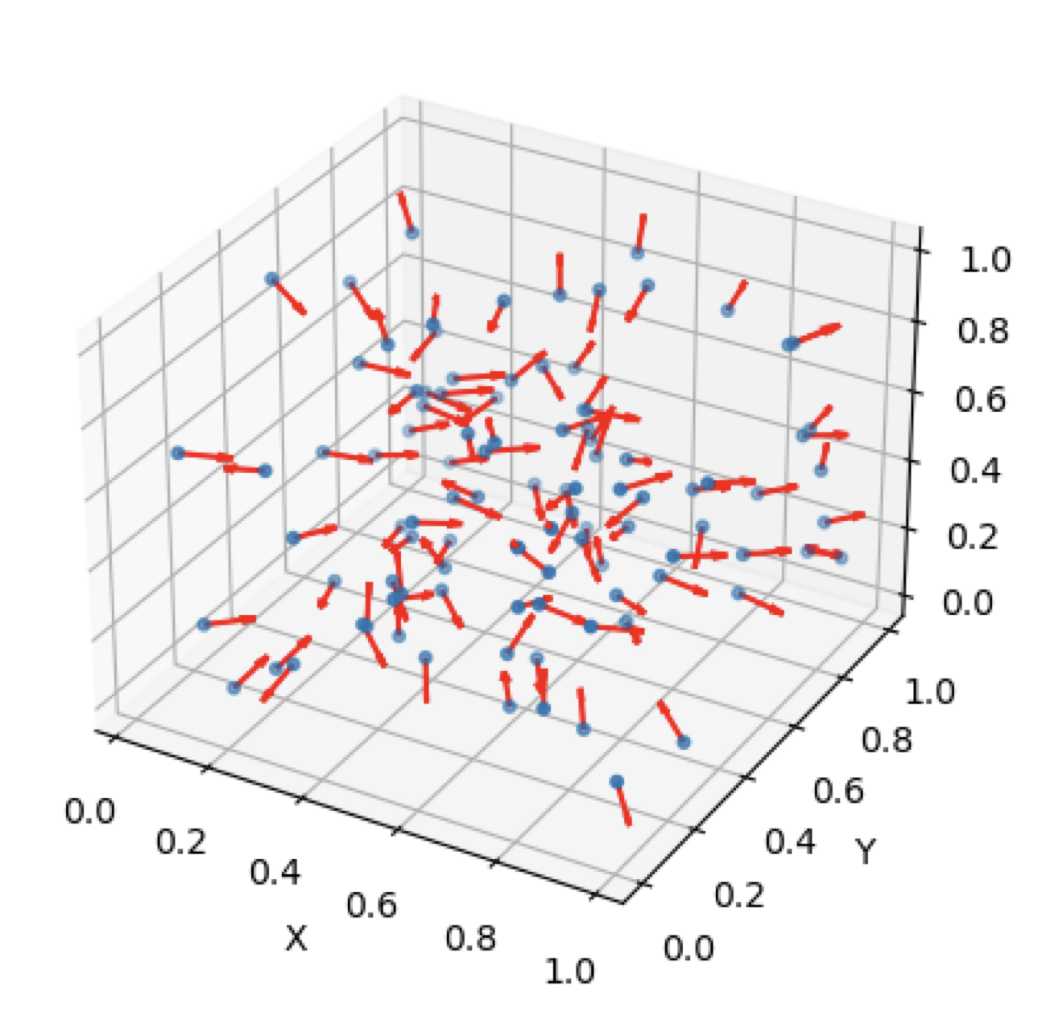
import numpy as np
import open3d as o3d
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 임의의 3D 데이터 생성
num_points = 100
x = np.random.rand(num_points)
y = np.random.rand(num_points)
z = np.random.rand(num_points)

# Open3D의 PointCloud 객체로 변환
pcd_ori = o3d.geometry.PointCloud()
pcd_ori.points = o3d.utility.Vector3dVector(np.column_stack((x, y, z)))

# 법선 벡터 계산
pcd_ori.estimate_normals()

# 3D 산점도 그리기
fig = plt.figure()
ax = fig.add_subplot(projection='3d')

# 포인트를 산점도로 그리기
ax.scatter(x, y, z, s=10)

# 법선 벡터를 화살표로 그리기
for i in range(len(pcd_ori.normals)):
    point = pcd_ori.points[i]
    normal = pcd_ori.normals[i]
    ax.quiver(point[0], point[1], point[2], normal[0], normal[1], normal[2], length=0.1, normalize=True, color='r')

# 축 레이블 설정
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

2. 중심점으로부터 현재 점으로의 벡터 구하기

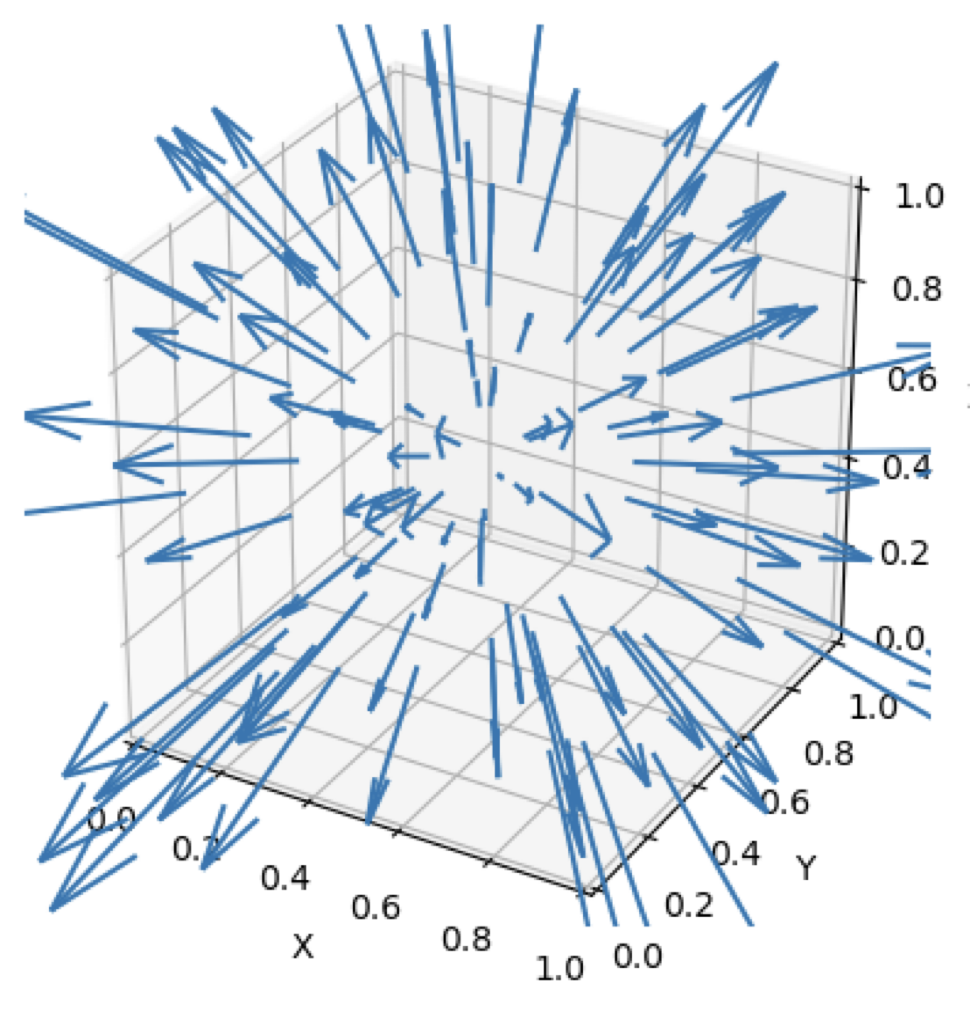
3. Covariance Matrix 의 Eigen Value, Eigen Vector 구하기

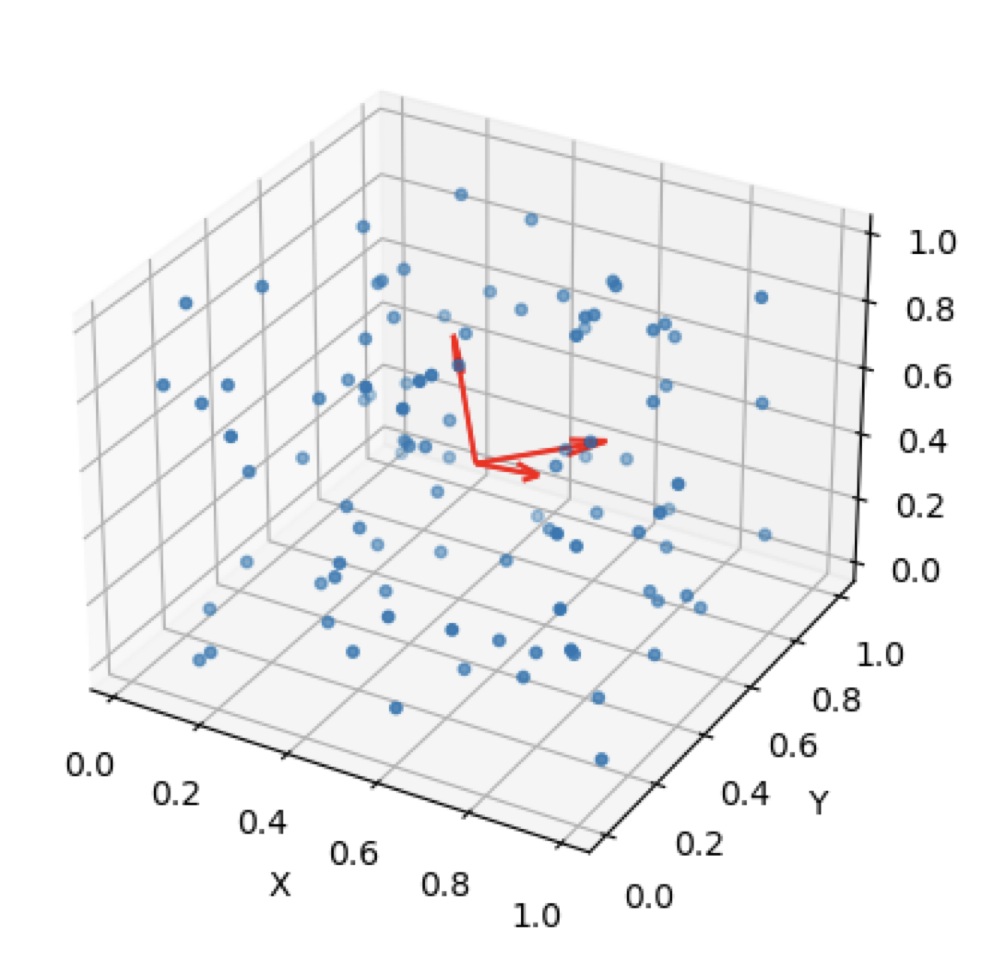
검증

Gaussian Distribution 의 분산값을 조정해서 Flat Data, Rough Data 를 임의로 생성한 후 시각화하였다.

각각에 대해 Surface Roughness 를 구한 결과,

예상했던 결과대로 Flat 한 데이터보다 Rough 한 데이터에서 Surface Roughness 값이 더 높게 나타났다.

데이터 분석

1. 데이터 사이의 상관 관계

데이터 개수 : 각 425개

• Surface Roughness 그래프

• Surface Roughness, Linear Acceleration, Angular Velocity 그래프

Raw 데이터만 가지고는 상관관계를 알기 어려웠기 때문에, 이를 정규화한 후 적분하였다.

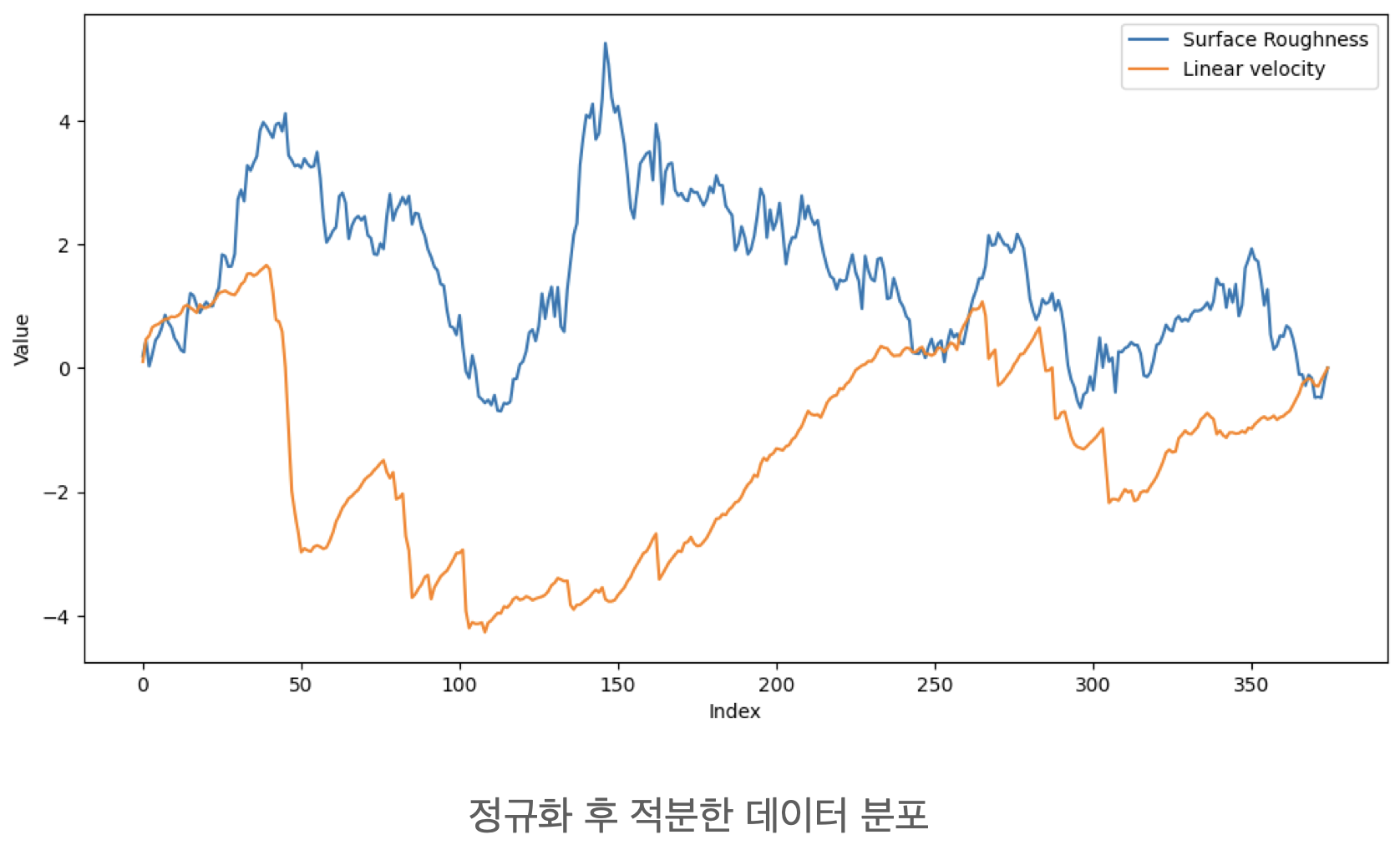
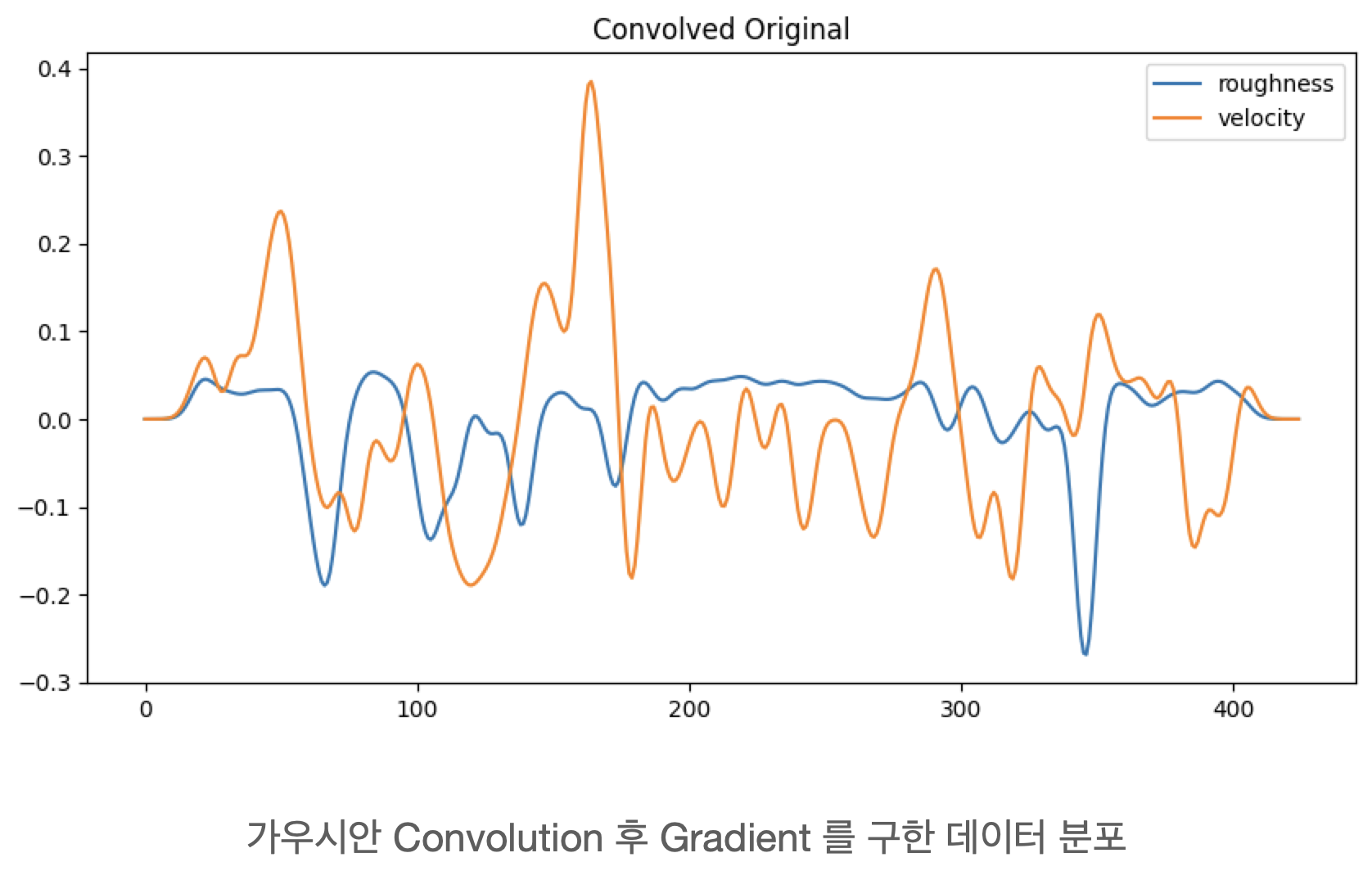
2. DNN 모델

1. 전처리 및 Correlation Coefficient 계산

import numpy as np
import torch
import matplotlib.pyplot as plt

def remove_outliers(linear_acceleration_list, angular_velocity_list, roughness_list):
    indices_to_remove = []
    for i, r in enumerate(roughness_list):
        if r < 1.525:
            indices_to_remove.append(i)

    linear_acceleration_list = np.delete(linear_acceleration_list, indices_to_remove, axis=0)
    angular_velocity_list = np.delete(angular_velocity_list, indices_to_remove, axis=0)
    roughness_list = np.delete(roughness_list, indices_to_remove, axis=0)

    return linear_acceleration_list, angular_velocity_list, roughness_list
    
linear_acceleration_list = remove_outliers(linear_acceleration_list, angular_velocity_list,roughness_list)[0]
angular_velocity_list = remove_outliers(linear_acceleration_list, angular_velocity_list,roughness_list)[1]
roughness_list = remove_outliers(linear_acceleration_list, angular_velocity_list,roughness_list)[2]

values = []
for fn in filenames:
    with open(f'list/{fn}') as file:
        arr = torch.tensor(eval(''.join(file.readlines())))
        arr = arr - arr.mean()
        arr = arr / arr.abs().max()
        arr = arr.cumsum(dim=0)
        values.append(arr)
        
    
x = torch.arange(len(values[0]))
angular_vel, linear_vel, roughness = values
labels = ['roughness', 'velocity']

plt.figure(figsize=(12,6))

print(np.corrcoef(roughness.numpy(), linear_vel.numpy()))

2. DNN 모델

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
import random

# 데이터셋 클래스 정의
class RoughnessDataset(Dataset):
    def __init__(self, roughness, linear_vel):
        self.roughness = roughness
        self.linear_vel = linear_vel

    def __len__(self):
        return len(self.roughness)

    def __getitem__(self, idx):
        return (self.roughness[idx], self.linear_vel[idx])
        
class RoughnessModel(nn.Module):
    def __init__(self):
        super(RoughnessModel, self).__init__()
        self.fc1 = nn.Linear(1, 10) # Fully Connected Layer 생성
        self.fc2 = nn.Linear(10, 10)
        self.fc3 = nn.Linear(10, 1)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.fc3(x)
        return x

learning_rate = 0.001
batch_size = 16
num_epochs = 100

dataset = RoughnessDataset(roughness, linear_vel)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

model = RoughnessModel()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

for epoch in range(num_epochs):
    for batch_idx, (data, target) in enumerate(dataloader):
        optimizer.zero_grad()
        data = torch.tensor(data).float() 
        target = torch.tensor(target).float()
        output = model(data.unsqueeze(1).float())
        loss = criterion(output, target.unsqueeze(1))
        loss.backward()
        optimizer.step()

    if epoch % 10 == 0:
        print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

torch.save(model.state_dict(), 'roughness_model.pt')

with torch.no_grad():
    input = torch.tensor([0.5])
    output = model(input.unsqueeze(0).float())
    print('Predicted linear velocity:', output.item())
    
#검증
test_dataset = RoughnessDataset(roughness, linear_vel)

# 검증용 데이터셋에서 무작위로 샘플 추출
sample_indices = np.random.choice(len(test_dataset), 100, replace=False)
test_samples = [test_dataset[i] for i in sample_indices]

model = RoughnessModel()
model.load_state_dict(torch.load('roughness_model.pt'))

# 모델 검증 및 정확도 출력
with torch.no_grad():
    correct = 0
    total = 0
    for data, target in test_samples:
        data = torch.tensor(data).float()  # NumPy 배열을 PyTorch 텐서로 변환
        target = torch.tensor(target).float()
        output = model(data.unsqueeze(0)).item()  # unsqueeze() 메서드는 PyTorch 텐서에서 사용 가능
        predicted = round(output)
        actual = round(target.item())
        if predicted == actual:
            correct += 1
        total += 1

    accuracy = correct / total
    print('Accuracy: {:.2f}%'.format(accuracy * 100))

3. 학습된 모델의 예측값 시각화

#학습된 모델의 예측값 시각화

import matplotlib.pyplot as plt

model = RoughnessModel()
model.load_state_dict(torch.load('roughness_model.pt'))

# 예측값 시각화용 roughness 리스트 생성
test_roughness = np.linspace(0, 1, 100)

with torch.no_grad():
    model.eval()
    test_inputs = torch.tensor(test_roughness).float().unsqueeze(1)
    predicted_outputs = model(test_inputs).squeeze(1)
    plt.plot(test_roughness, predicted_outputs, label='Predicted')

plt.xlabel('Roughness')
plt.ylabel('Linear velocity')
plt.title('Predicted linear velocity vs. roughness')
plt.legend()
plt.show()

3. 결과

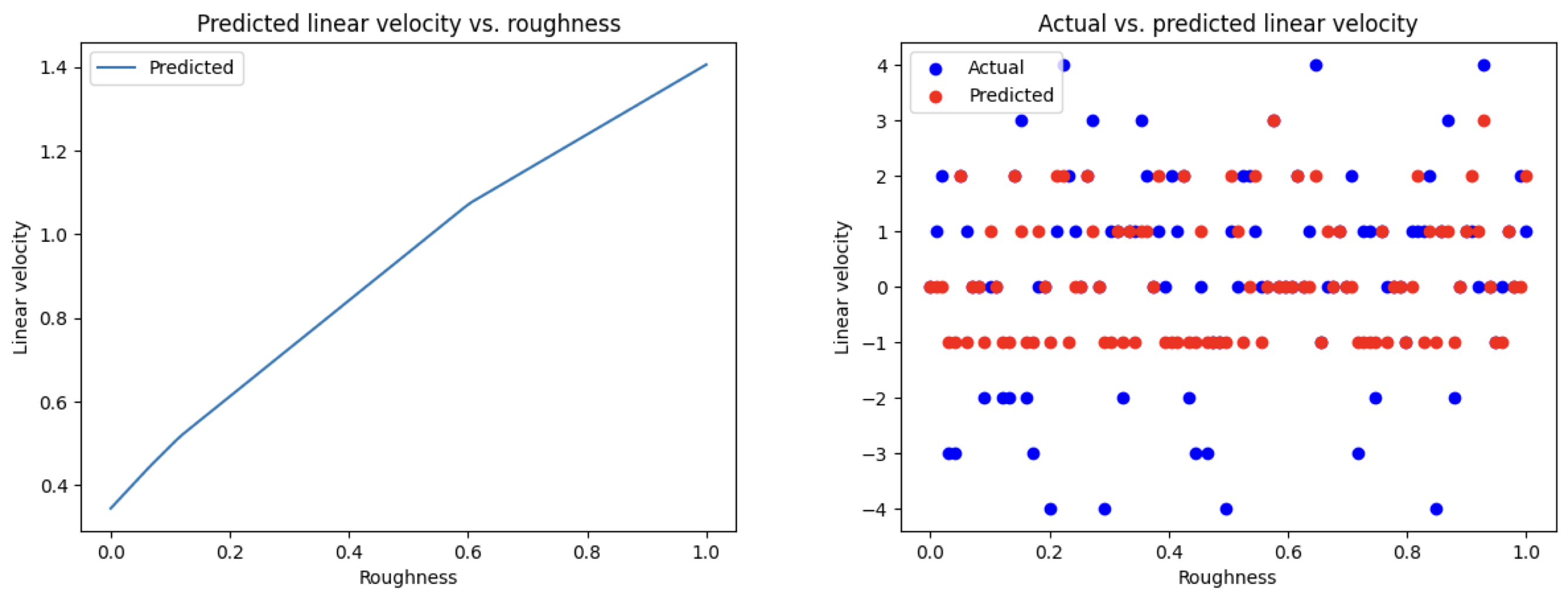
모델 학습 결과는 다음과 같다.

피드백

교수님께서 해 주신 말씀음 다음과 같다.

1. IMU 센서는 노이즈가 많은데, 이 값을 적분해서 속도를 구해 시간차를 구하는 과정에서 너무나 많은 불확실성이 있다.
2. IMU 데이터 중 Linear Acceleration 값을 사용한 이유가 명확하지 않다.
3. 같은 이유로, 도로의 울퉁불퉁함과 IMU 데이터 사이의 상관관계가 불분명하다.
4. 모델의 정확도가 높다고 하는건 아무 의미가 없다. 왜냐면 넣은 데이터대로 그냥 학습하는 것 뿐이기 때문에.
5. 데이터 사이의 상관관계가 없어 보인다.
6. Surface Roughness 라는 수치들 간의 차이가 너무 적다.