Introduction

저자는 transformer의 inference time에 많은 시간이 들어간다고 지적하고 있다. 왜냐하면 기존의 autoregressive MT(MT: machine translation)는 이전의 시퀀스를 받아서 현 시퀀스를 생성하는 꼴이다. 이렇게 한번에 하나의 토큰을 생성하는 것은 MT system에 휴대성을 제한한다.
이러한 이슈로 인해 등장한 것이 바로 NAT이다. Non-autoregressive machine translation model이라고 하는데, 이름 그대로 non-autoregressive하다. 이는 병렬적으로 문장을 생성한다. NAT의 단점 말하며, 새로운 디코딩 알고리즘을 통해 극복할 수 있다고 한다.

왼쪽의 그림이 autoregressive decoding을 수행하는 MT이다. 오른쪽은 parallel decoding을 하는 사진이다. 오직 바뀐 것은 decoding algorithm 뿐이다.

Related Work

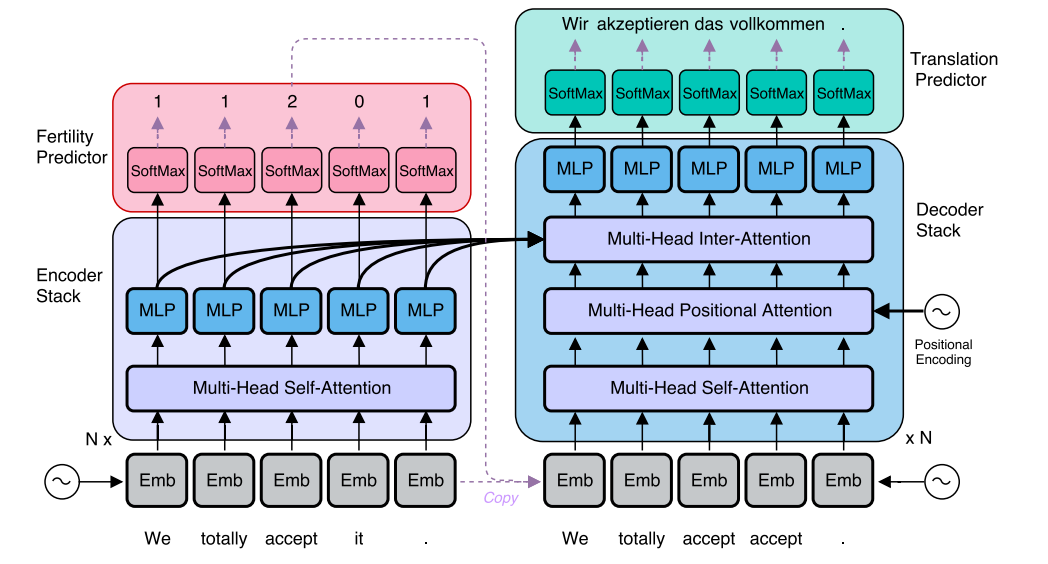
NAT의 아키텍처이다. 빨간색 박스로 되어있는 부분이 Fertility Predictor인데 이것이 차이점을 만든다. 이 박스 위에 (1, 1, 2, 0, 1)이라는 숫자가 있는데, 이는 단어가 몇번 반복될 것인지 나타내는 것이다. 예를 들어 "l like your shirt"라는 문장은 "네 셔츠 마음에 들어"라는 문장으로 번역될 수 있으므로 (0, 2, 1, 1)가 된다. like라는 단어가 "마음에 들어"라는 2단어가 되었기 때문이다.
그러나 이러한 NAT는 문제가 있다. 1)MT system을 complete reengineering해야 한다. 2)광범위한 training resource를 요구한다. 3)더 큰 autoregressive model로부터 distillation해야한다. 이때 distillation은 지식 증류라고 말할 수 있으며, 더 큰 모델이 학습한 결과를 증류하여 작은 모델을 학습시키는 것이다.

Method

notation

x = (x1, . . . , xn)
y = (y1, . . . , ym)
x1:n = (x1, . . ., xn)
pθ(y | x) -> x가 주어졌을 때 y의 확률

greedy search를 하는 autoregressive MT model은 yi를 yi = arg max pθ(yi | y1:i−1, x) 이러한 수식을 이용해서 찾아낸다.

이때 argmax는 주어진 함수를 최대화하는 연산을 찾는다. 즉, pθ(yi | y1:i−1, x)를 최대화하는 yi를 찾는다는 것이다. 이 수식을 기반으로 m번 추론 스텝을 밟으며 m개의 output sequence를 뽑아낸다.

parallel decoding algorithm

이 논문에서는 Jacobi와 Gauss-Seidel(GS) 고정점 반복 방법(Ortega and Rheinboldt, 1970)에 의존하여 정지 조건에 도달할 때까지 병렬 시스템으로 아래의 방정식(4)를 해결한다.

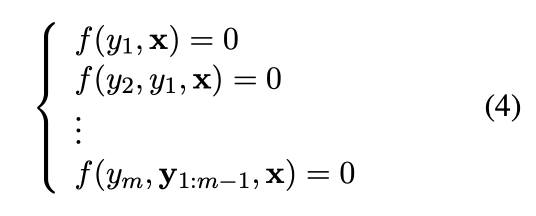
Jacobi와 GS 고정점 반복 방법이란?

두 방법은 모두 연립방정식을 iteration을 이용해 풀어내기 위한 것이다.

Jacobi iteration(J는 묵음이애오)

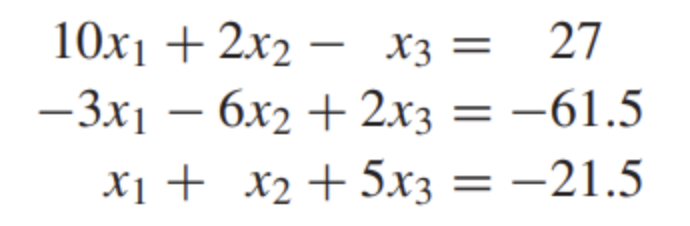
x1, x2, x3의 해를 알기 위해서 먼저 xn = ~ 꼴이 되도록 식을 정리해준다.

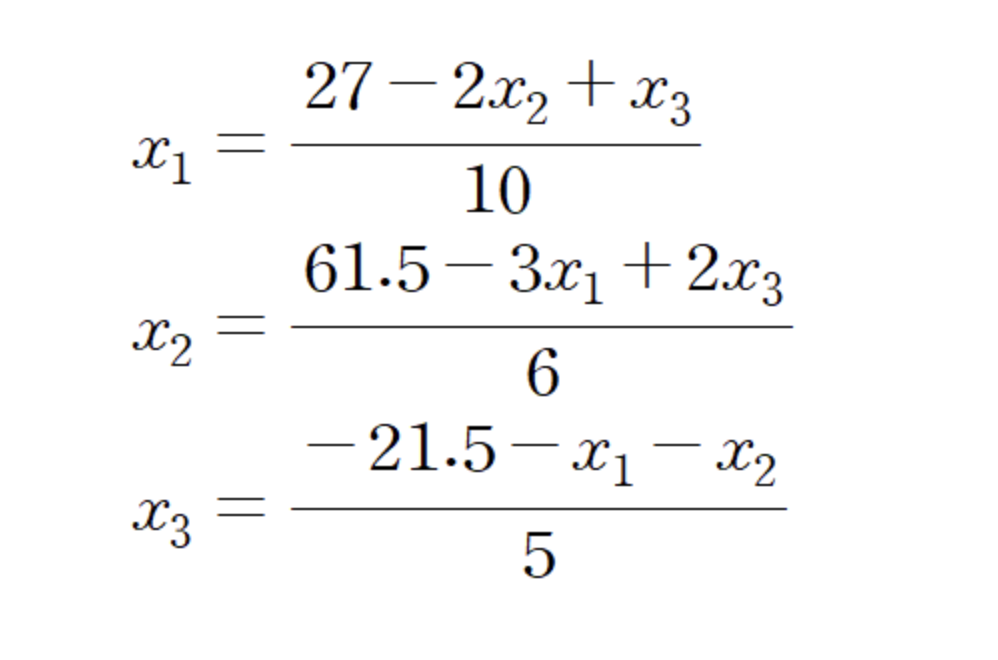
이렇게 정리된 방정식에 초기값 (0, 0, 0)을 대입해준다.

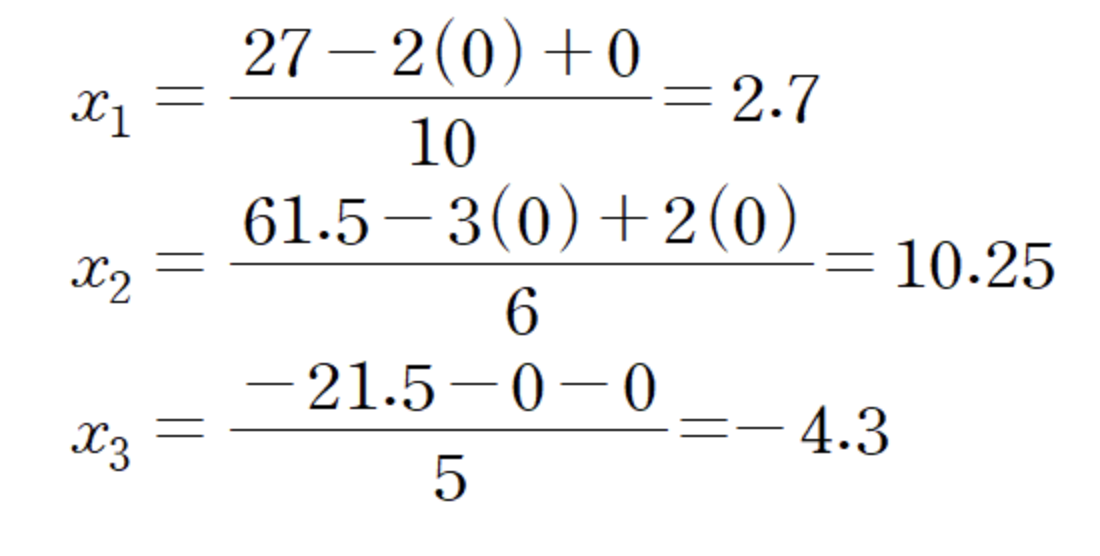
iter1의 결과는 (2.7, 10.25, -4.3)이다. 해당 해를 x1, x2, x3 자리에 대입하고 다시 계산해준다.

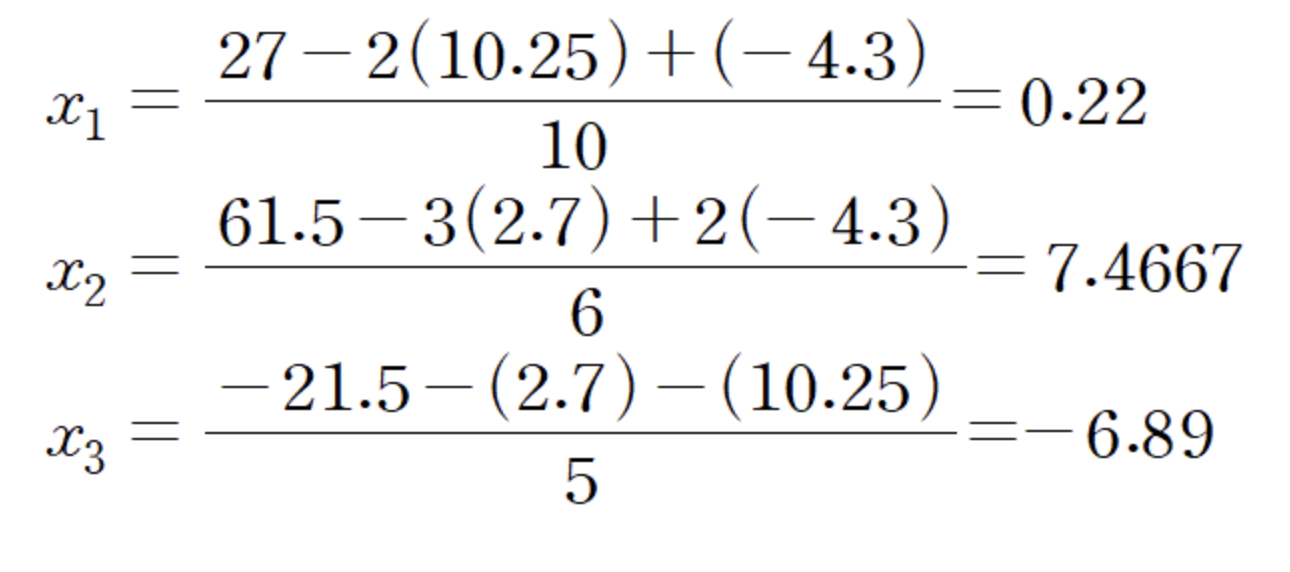
이렇게 한꺼번에 업데이트 해가며 수렴하는 해를 찾는 것이 야코비 반복법이다.

Gauss-Seidel Method(줄여서 GS method라고 한다.)

위의 야코비 반복법을 이해했다면 간단하다.

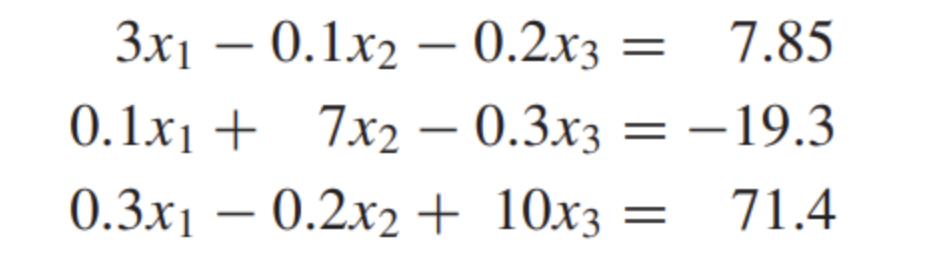
해당 연립방정식을 풀어보자. 야코비처럼 식을 정리해주고, (0, 0, 0)을 대입해준다.

대입 후 차이점이 있다. 야코비는 한번에 x1, x2, x3 값을 update해주었다면 GS는 순차적으로 업데이트를 한다. 먼저 x1 식에 (0, 0, 0)을 대입해서 x1을 구한다.

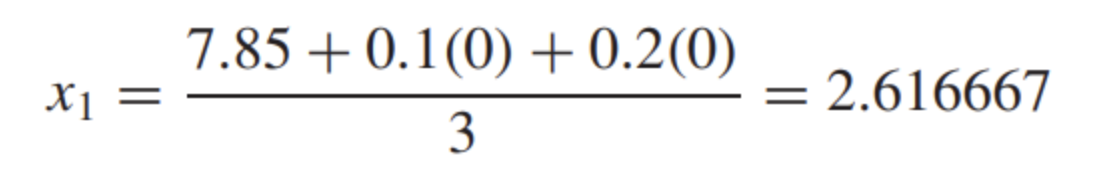
x1 = 2.616667이다. 이 x1을 x2를 구할 때 이용하는 것이다. 그렇다면 x2를 구하기 위해 x1, x2, x3 = (2.616667, 0, 0)이 되는 것이다.

이런 식으로 수렴하는 해가 될 때까지 반복하는 것이다.

총 3가지의 디코딩 알고리즘이 있는데 PJ, PGJ, HGJ decoding이다.
이때 PJ, PGJ는 타켓 문장의 길이를 m으로 알고 있다고 가정해야 한다.

Parallel Jacobi Decoding (PJ)

전체 타겟 문장에 대한 초안 번역을 초기화한 후, 중단 조건이 발동될 때까지 전체 문장을 병렬로 반복적으로 번역하는 방식으로 작동한다. 이는 Jacobi iteration으로 방정식을 해결하는 것과 동일하게 동작한다.

Parallel GS-Jacobi Decoding (PGJ)

이름에서 볼 수 있듯이 이는 GS와 야코비 둘 다 사용한다. 예를 들어서 설명하겠다.
"The cat is on the mat"이라는 문장을 디코딩한다고 할 때, 먼저 "the cat is" 부분 (y1, y2, y3)을 Jacobi 방식으로 병렬 처리한다. 그 후, 나머지 문장인 "on the mat" 부분 (y4, y5, y6)을 디코딩하는데 이 때 이전 블록의 결과인 (y1, y2, y3)를 사용한다.

Hybrid GS-Jacobi Decoding (HGJ)

사실 기계 번역은 EOS(end of sentence)를 이용해 동적으로 문장의 길이를 조정한다. 그런데 PJ와 PGJ의 경우는 m 길이를 가정한다고 한다. 이러한 문제를 해결하기 위해서 나타난 것이 HGJ이다.
HGJ는 h라는 특정 고정 길이를 갖는다. 만약 h 단어 이내에서 EOS가 생성되면 PGJ 방식으로 해결하고, h 길이가 넘어갔는데 EOS가 생성되지 않았다면, 표준 autoregressive decoding을 수행한다.

initialization and stopping

[PAD] 토큰으로 초기화한다. PAD 토큰을 예를 들어 설명하자면, 만약 "안녕하세요"라는 문장을 처리하고, 모델이 10개의 토큰을 요구한다면, 나머지 5개의 토큰은 PAD 토큰으로 채워질 수 있습니다. 여기서 향후 연구에서 다른 초기화 절차를 탐구하여 디코딩 속도를 더욱 향상시킬 것을 제안했다.

stop function은 속도 향상과 번역 품질 간 균형을 조절하기 때문에 중요하다. 이 논문에서는 stop condition을 yk-1 - yk = 0으로 하였다. 즉, 이전 결과와 현재의 결과가 다르지 않을 때 iteration을 멈춘다는 것이다.

Experiments

데이터셋은 아래의 것들을 사용했다고 하고, 모든 데이터셋을 양방향으로 평가했다고 한다.
WMT14 English-German [En-De]: 영어에서 독일어로의 번역을 위한 데이터셋.
WMT16 English-Romanian [En-Ro]: 영어에서 루마니아어로의 번역을 위한 데이터셋.
IWSLT15 English-Vietnamese [En-Vi]: 영어에서 베트남어로의 번역을 위한 데이터셋.
IITB English-Hindi [En-Hi]: 영어에서 힌디어로의 번역을 위한 데이터셋.
WMT17 English-Finnish [En-Fi]: 영어에서 핀란드어로의 번역을 위한 데이터셋.
FLORES-101 English-Italian [En-It]; English-French [En-Fr]: 영어에서 이탈리아어, 영어에서 프랑스어로의 번역을 위한 데이터셋.

evaluation을 위해서 BLEU 방식을 썼다.

BLEU(Bilingual Evaluation Understudy) 방식은 기계 번역의 품질을 평가하는 방법입니다. 번역된 문장이 얼마나 사람이 번역한 문장과 유사한지를 측정하여 점수를 매깁니다.

Algorithms comparison

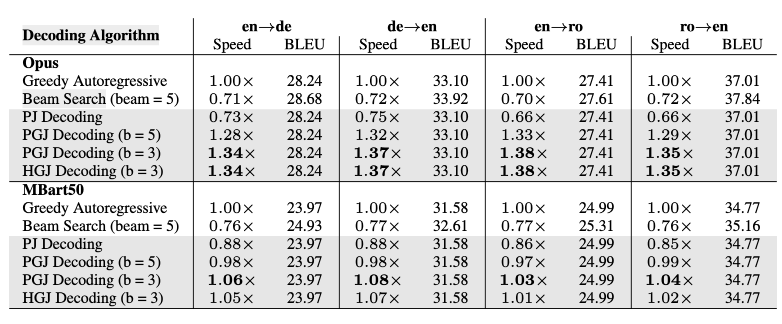
Table1을 보면 PGJ, HGJ가 가장 빠른 알고리즘임을 알 수 있다. 또한, greedy autoregressive algorithm과 동일한 번역 품질을 보장함을 알 수 있다.
table1은 beam size=5인 알고리즘이 BLEU 스코어 면에서 우수하다는걸 보여주는데, 이는 speed를 희생한 결과이다.
이때 beam search보다 parallel decoding이 BLEU 점수가 더 낮다는 것은, 병렬 디코딩도 speedup과 번역품질을 trade-off한다는 것을 의미한다.
다른 특징은 PJ와 PGJ(b=5)일 때, greedy autoregressive 보다 느리다는 것이다. 이것은 몇몇의 요인들이 있다.
긴 시퀀스에서는 CPU/GPU가 많은 메모리 엑세스를 필요로 하기 때문에 이것은 연산량을 느리게 할 수 있다는 것이다. 이러한 computational overhead는 실제 실행을 느리게 할 수 있다. 또한, MBart50과 Opus 사이의 속도 향상 차이에 대해서도 이 오버헤드가 영향을 미친다. 이는 computational scaling에서 더 자세하게 다룬다.

Analysis and validation

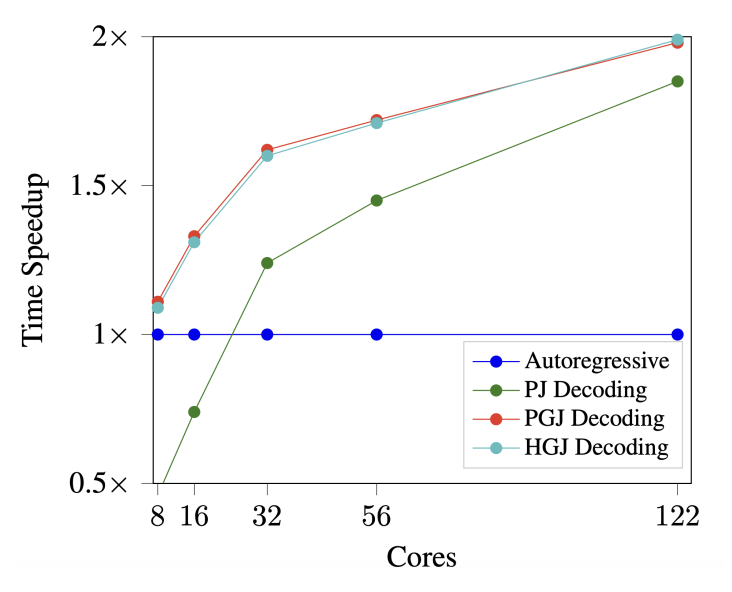
core에 따라서 time speedup이 얼마나 바뀌는지 알 수 있는 그래프이다. 그래프에서 PJ를 보면 8코어는 너무 제한적인 리소스임을 알 수 있다.
저자의 method들은 리소스가 증가할 수록 더 효율적으로 동작한다.
(해당 그래프는 실제 환경의 결과가 아닌 컴퓨팅이 병렬적으로 최적화 되었을 때 얻을 수 있는 잠재적 결과이다.) -> 질문: 122코어를 현실세계에서 돌리려면 돈이 얼마나.. 들까? 천만원..

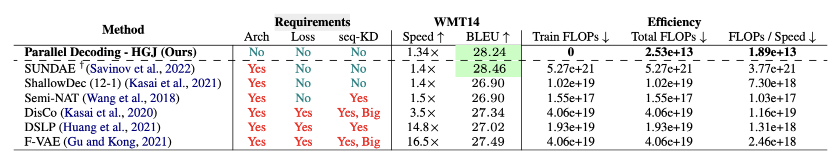
• arch(architecture) : 아키텍쳐의 수정이 필요한지
  loss : 모델 학습 시 추가적인 손실함수가 필요한지
  seq-KD (Sequence Knowledge Distillation) : 지도 학습 과정에서 시퀀스 수준의 지식을 다른 모델로부터 전달(distill)받는 과정을 필요로 하는지
  Table3이다. 이는 NAT와 저자의 알고리즘을 비교한다. "SUNDAE," "Shallow-Dec," "Semi-NAT," "DisCo," "DSLP," 그리고 "F-VAE"는 모두 NAT이다.
  SUNDAE와 HGJ를 비교해보자. 스피드와 BLEU 모두 딸리지만... SUNDAE는 더 많은 리소스를 필요로 한다는 것이다!
  다시 한번 저자는 학습이나 수정없이 현재 모델의 속도를 향상시킬 수 있음을 강조한다.

visualizing parallel decoding

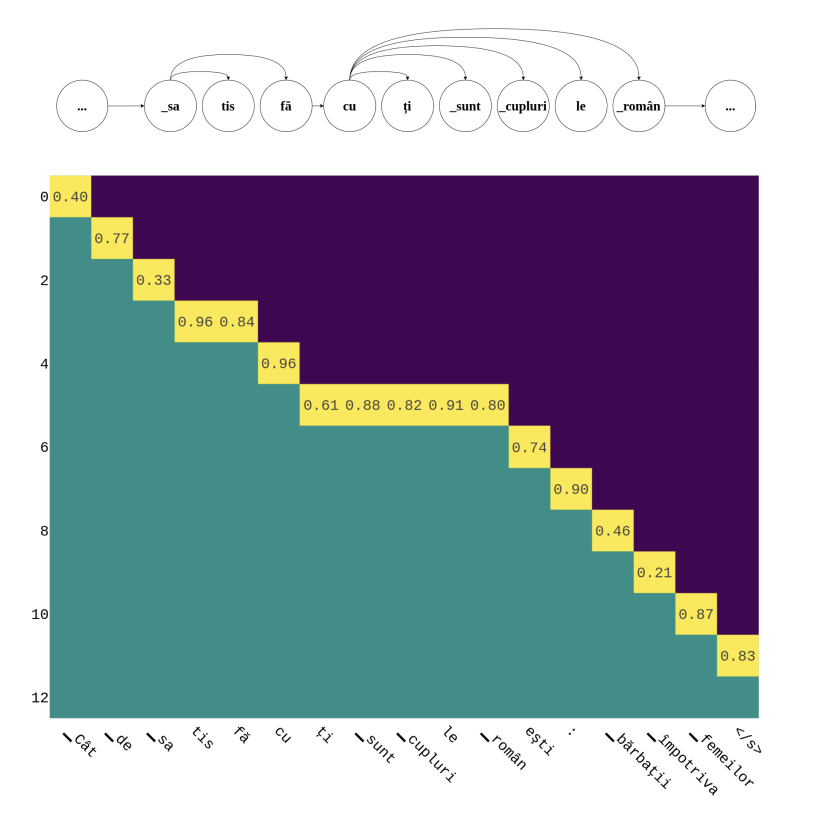
위 그림은 DDGviz(Decoding Dependency Graph visualizer)라고 한다.
x축: 특정 시점에 생성된 토큰
y축: iteration 횟수
예로 들자면, iteration=5일 때 한번에 ti sunt cuplurile roman이 생성된다.

이 그래프를 통해서 우리는 뽑아낼 수 있는 정보가 있다.
“How satisfi_” 뒤에 “_ed are the Romanian couples”라는 문장이 병렬적으로 나오는 것은 특수한 케이스이다. 그 예측이 지나치게 제한적이거나주는데, 이러한 편향이 위험할 수 있음을 알아야한다.

그 예측이 지나치게 제한적이거나, 데이터의 편향된 부분을 반영한다면, 이는 번역의 질을 떨어뜨리고 의도하지 않은 편향을 만들어낼 수 있다는 것이다.

Conclusions

저자들은 해당 방법이 훈련, 수정 또는 품질 손실 없이 일관된 속도 향상을 달성하는 세 가지 병렬 디코딩 방법이라고 하였다. 저희 방법에 단점이 없는 것은 아니지만 병렬 수준 디코딩 알고리즘을 모든 모델에 통합하기 위한 첫 번째 귀중한 단계라고 한다.
이 방법은 NAT가 실행될 수 없는 제한된 리소스 환경이거나, fine-grained 또는 문자(character) 단위 트랜스포머 모델의 속도를 높이는데 관련이 있다.

Limitation

제안된 parallel decoding이 기존 모델의 속도를 개선할 수 있으나, 고려해야 할 점이 있다.

병렬 리소스 필요성

실제 벽시계 시간(wall-clock time)에서의 속도 향상을 경험하기 위해서는 병렬 연산을 수행할 수 있는 환경이 필요하다. 병렬 리소스나 병렬 최적화 소프트웨어 없이 병렬 디코딩을 사용하면 오버헤드로 인해 실제 실행 시간이 늘어날 수 있다.

추론 단계에서의 추가 계산 비용

추론 단계에서 추가적인 계산 비용이 발생한다는 것을 의미하며, 속도 향상을 달성하기 위해 필요하다. 원하는 가속도와 추가 시간 사이 trade-off를 잘 생각해야 한다.

Beam search과의 결합 어려움

beam search는 본질적으로 dynamic programming 방법이다. 따라서, 순차적인 계산을 필요로 한다. 때문에 병렬 디코딩과 결합하기 어렵다는 단점이 있다.