📂4.1. 분류(Classification)

지도학습

• 레이블(label), 명시적인 정답이 있는 데이터가 주어진 상태에서 학습하는 머신러닝 방식

분류(classification)

• 지도학습의 한 유형
• 학습 데이터로 주어진 데이터의 피처와 레이블값(결정값, 클래스값)을 학습해 모델을 생성하고, 이 모델에 새로운 데이터값이 주어졌을 때 레이블 값을 예측하는 것
• 분류를 구현하는 머신러닝 알고리즘
  • 나이브 베이즈(naive bayes) : 베이즈(bayes) 통계와 생성 모델에 기반함
  • 로지스틱 회귀(logistic regression) : 독립변수와 종속변수의 선형 관계성에 기반함
  • 결정 트리(decision tree) : 데이터 균일도에 따른 규칙 기반
  • 서포트 벡터 머신(suport vector machine) : 개별 클래스 간의 최대 분류 마진을 효과적으로 찾음
  • 최소 근접(nearest neighbor) 알고리즘 : 근접 거리를 기준으로 함
  • 신경망(neural network) : 심층 연결 기반
  • 앙상블(ensemble) 서로 다르거나 같은 머신러닝 알고리즘을 결합함

앙상블 방법(Ensemble Method)

• 정형 데이터 예측 분석영역에서 높은 예측 성능을 보임
• 많은 '약한 학습기(예측 성능이 상대적으로 떨어지는 알고리즘)'를 결합 -> 확률적 보완과 오류 발생 부분에 대한 가중치를 계속 업데이트 -> 예측성능 향상
• 기본 알고리즘으로 일반적으로 결정트리를 사용
• '약한 학습기'로 결정 트리를 잘 사용함
• 배깅(bagging)과 부스팅(boosting) 방식으로 나뉨
  • 배깅(bagging) : 랜덤 포레스트(random forest) 등이 속함
  • 부스팅(boosting)
    근래 앙상블 방법은 부스팅 방식으로 지속해서 발전함
    그래디언트 부스팅(gradient boosting), XGBoost(eXtra Gradient Boost), LightGBM 등이 있음

결정 트리

• 데이터의 스케일링이나 정규화 등의 사전 가공 영향이 적음
• 과적합이 발생해 반대로 예측 성능이 저하될 수 있음

🌲4.2. 결정 트리

결정 트리(Decision Tree)

• 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만드는 것
• 데이터의 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적 분류인지가 알고리즘의 성능 좌우
• 데이터셋에 피처가 있고 이런 피처가 결합해 규칙 조건을 만들 때마다 규칙 노드가 만들어짐
  • 많은 규칙 -> 분류 결정 방식이 복잡해짐 -> 과적합이 되기 쉬움 -> 트리 깊이가 깊어질수록 결정트리 예측 성능 저하 가능성 있음
  • 가능한한 적은 결정 노드로 높은 예측 정확도 가지려면?
    • 데이터 분류 시, 최대한 많은 데이터셋이 해당 분류에 속하도록 결정 노드의 규칙 정해져야 함
    • 최대한 균일한 데이터 세트를 구성하도록 분할해야 함
• 데이터셋의 균일도
  • 데이터 구분 시 필요한 정보양에 영향을 미침
  • 결정 노드는 정보 균일도가 높은 데이터셋을 먼저 선택하도록 규칙 조건 만듦
• 정보 균일도 측정 방법
  • 정보 이득(information gain)
    • 엔트로피(주어진 데이터 집합의 혼잡도) 기반
    • 서로 다른 값이 섞이면 엔트로피가 높음
    • (정보이득지수) = 1 - (엔트로피 지수)
    • 정보 이득이 높은 속성을 기준으로 분할함
  • 지니 계수
    • 0이 가장 평등하고 1이 가장 불평등
    • 지니계수가 낮을수록 데이터 균일도가 높음 -> 낮은 속성을 기준으로 분할
• 사이킷런 결정 트리 알고리즘 : DecisionTreeClassifier
  • 지니 계수를 이용해 데이터셋 분할
  • 정보 이등 높거나 지니 계수 낮은 조건 찾음 -> 자식 트리 노드 걸쳐 반복적 분할 -> 데이터가 모두 특정 분류 속하면 분할 멈춤 -> 분류 결정

결정 트리 모델의 특징

• 정보의 균일도라는 룰을 기반으로 함 -> 알고리즘 쉽고 직관적
• 룰이 매우 명확 & 이를 기반으로 규칙 노드와 리프 노드 만들어지는지 알 수 있음
• 시각화로 표현 가능
• 각 피처의 스케일링과 정규화 등 전처리 작업 필요 없음. 사전 가공 영향도 크지 않음
• 과적합으로 정확도가 떨어짐
• 서브트리 계속 만들다보면 깊이 깊어지고 복잡해짐
• 트리 크기를 사전에 제한하는 것이 성능 튜닝에 더 도움이 됨

결정 트리 파라미터

• DecisionTreeClassifier(분류를 위한 클래스) / DecisionTreeRegressor(회귀를 위한 클래스)
• 사이킷런의 결정 트리 구현은 CART(Classification And Regression Trees) 알고리즘 기반
• 파라미터
  • min_sample_split [default=2]
    • 노드 분할하는 최소한의 샘플 데이터 수
    • 과적합 제어에 사용
    • 작게 설정할수록 분할되는 노드 많아져 과적합 증가
  • min_smaples_leaf
    • 말단 노드(leaf)가 되기 위한 최소한의 샘플 데이터 수
    • 과적합 제어용
    • 비대칭적 데이터의 경우 특정 클래스 데이터 매우 작을 수 있으므로 작게 설정해야 함
  • max_features
    • 최적의 분할 위해 고려할 최대 피처 개수
    • 디폴트는 None : 데이터셋의 모드 피처 대상 분할 수행
    • inf, float, log 등 옵션 있음
  • max_depth
    • 트리 최대 깊이
    • 디폴트는 None : 완벽하게 클래스 결정값이 될때까지 깊이를 계속 키우며 분할. min_samples_split 보다 작아질 때까지 깊이 증가시킴
    • 깊이 깊어지면 과적합 가능
  • max_leaf_nodes : 말단 노드의 최대 개수

결정 트리 모델의 시각화

• Graphviz 패키지 사용
• export_graphviz() API 제공 : 함수 인자로써 학습이 완료된 estimator, 피처 이름 리스트, 레이블 이름 리스트 입력
• 파이썬과 인터페이스할 수 있는 Wrapper 모듈을 별도 설치 해야함

### 모듈 임포트

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import export_graphviz
from sklearn.datasets import make_classification
import graphviz
import warnings
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
warnings.filterwarnings('ignore')


dt_clf = DecisionTreeClassifier(random_state=156)
iris_data = load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, test_size=0.2, random_state=11)
dt_clf.fit(x_train, y_train)

export_graphviz(dt_clf, out_file="tree.dot", class_names =iris_data.target_names, \
               feature_names=iris_data.feature_names, impurity=True, filled=True)
with open("tree.dot") as f:
    dot_graph = f.read()
graphviz.Source(dot_graph)

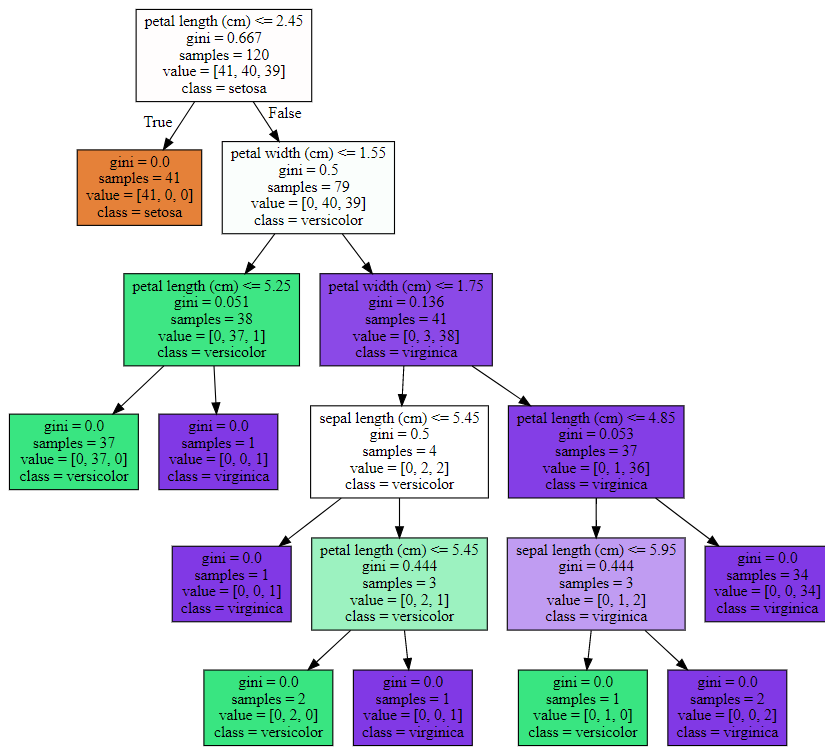
하이퍼 파라미터

• 복잡한 트리가 생성되는 것을 방지
• max_depth : 결정 트리의 최대 깊이 제어
• min_samples_splits : 자식 규칙 노드를 분할해 만들기 위한 최소한의 샘플 데이터 개수
• min_damples_leaf : 리프 노드가 될 수 있는 샘플 데이터 건수의 최솟값
  • 디폴트=1
    • 다른 클래스 값이 하나도 없이 단독 클래스로만 되어 있거나
    • 단 한 개의 데이터로 되어있을 때는 리프 노드가 될 수 있음
  • min_samples_leaf <= (지정값) 기준을 만족해야 리프 노드가 될 수 있음

feature_importances 속성

• 어떤 속성을 규칙 조건으로 선택하는가가 중요함
• 중요 몇 개 피처가 명확한 규칙 트리 만드는 데 기여 -> 모델을 간결하고 이상치(outlier)에 강한 모델 만들 수 있음
• 사이킷런에서는 규칙 정할 때 피처의 중요한 역할 지표를 DecisionTreeClassifier.feature_importances_속성으로 제공
  • 넘파이 배열 형태로 값 반환 & 피처 순서대로 값 할당됨
  • 값이 높을수록 해당 피처의 중요도가 높다는 의미임

print('Feature importances\n')
for name, value in zip(iris_data.feature_names, dt_clf.feature_importances_):
    print('{0} : {1:.3f}'.format(name, value))
sns.barplot(x=dt_clf.feature_importances_, y=iris_data.feature_names)

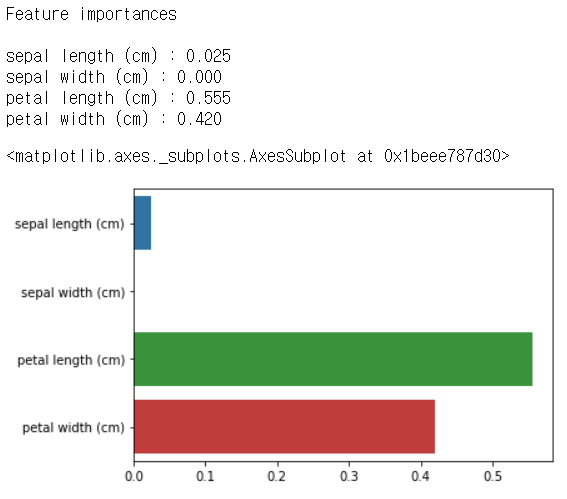
트리 과적합

• 사이킷런은 분류 위한 테스트용 데이터 쉽게 만드는 make_classification() 함수 제공
• 아래 예는 2개의 피처가 3가지 유형의 클래스 값을 가지는 데이터셋을 만들고, 이를 시각화해보자

x_features, y_labels = make_classification(n_features=2, n_redundant=0, n_informative=2, n_classes=3, n_clusters_per_class=1, random_state=0)
plt.scatter(x_features[:, 0], x_features[:, 1], marker='o', c=y_labels, s=25, edgecolor='k')

• 결정 트리 생성시 어떤 결정 기준 가지고 분할하며 데이터 분류하는지 확인하자

#머신러닝 모델이 클래스 값을 예측하는 결정 기준을 색상&경계로 나타내는 함수
def visualize_boundary(model, X, y):
    fig,ax = plt.subplots()
    
    # 학습 데이타 scatter plot으로 나타내기
    ax.scatter(X[:, 0], X[:, 1], c=y, s=25, cmap='rainbow', edgecolor='k',
               clim=(y.min(), y.max()), zorder=3)
    ax.axis('tight')
    ax.axis('off')
    xlim_start , xlim_end = ax.get_xlim()
    ylim_start , ylim_end = ax.get_ylim()
    
    # 호출 파라미터로 들어온 training 데이타로 model 학습 . 
    model.fit(X, y)
    # meshgrid 형태인 모든 좌표값으로 예측 수행. 
    xx, yy = np.meshgrid(np.linspace(xlim_start,xlim_end, num=200),np.linspace(ylim_start,ylim_end, num=200))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
    
    # contourf() 를 이용하여 class boundary 를 visualization 수행. 
    n_classes = len(np.unique(y))
    contours = ax.contourf(xx, yy, Z, alpha=0.3,
                           levels=np.arange(n_classes + 1) - 0.5,
                           cmap='rainbow', clim=(y.min(), y.max()),
                           zorder=1)

• 위에서 만든 데이터로 시각화

dt_clf = DecisionTreeClassifier().fit(x_features, y_labels)
visualize_boundary(dt_clf, x_features, y_labels)

• 하이퍼 파라미터 min_samples_leaf 수정

dt_clf = DecisionTreeClassifier(min_samples_leaf=6).fit(x_features, y_labels)
visualize_boundary(dt_clf, x_features, y_labels)