논문 번역

• 이 글은 제가 읽는 논문을 번역해서 올려놓는 공간입니다.
• 번역은 LLM(현재는 GPT-4)를 통해 번역하고 있습니다.
• 대략의 pipeline은 mathpix를 통해 ocr후 gpt-4로 대략 1000토큰 단위로 나누어 번역하고 있습니다. 논문->ocr을 통한 markdown으로 변경 -> markdown로 작성된 논문을 gpt-4 api로 번역 및 markdown으로 작성
• 현재까지 완성된 파이프라인은 https://github.com/aeolian83/paper_translator 입니다
• 원문 링크는 다음과 같습니다.
  • https://paperswithcode.com/paper/diffusion-models-a-comprehensive-survey-of

확산 모델: 방법론과 응용에 대한 종합적인 조사

LING YANG ${ }^{*}$, 중국 북경대학교

ZHILONG ZHANG ${ }^{*}$, 중국 북경대학교

YANG SONG, OpenAI, 미국

SHENDA HONG, 중국 북경대학교

RUNSHENG XU, 캘리포니아 대학교 로스앤젤레스, 미국

YUE ZHAO, 카네기 멜론 대학교, 미국

YINGXIA SHAO, 중국 베이징 우편전신대학교

WENTAO ZHANG, Mila - 퀘벡 인공지능(AI) 연구소, HEC 몬트리올, 캐나다

BIN CUI, 중국 북경대학교

MING-HSUAN YANG, 캘리포니아 대학교 머시드, 미국

확산 모델은 이미지 합성, 비디오 생성, 분자 설계 등 많은 응용 분야에서 기록적인 성능을 보여주는 새로운 강력한 딥 생성 모델(deep generative models)의 한 분야로 부상하고 있습니다. 이 조사에서는 확산 모델에 대한 빠르게 확장되는 연구를 개관하고, 연구를 효율적인 샘플링, 개선된 가능도 추정(improved likelihood estimation), 특수 구조를 가진 데이터 처리의 세 가지 주요 영역으로 분류합니다. 또한 확산 모델을 다른 생성 모델과 결합하여 결과를 향상시킬 수 있는 잠재력에 대해서도 논의합니다. 컴퓨터 비전, 자연어 처리, 시계열 데이터 모델링에서부터 다른 과학 분야의 학제간 응용에 이르기까지 확산 모델의 광범위한 응용 분야를 추가로 검토합니다. 이 조사는 확산 모델의 현재 상태에 대한 맥락화되고 심층적인 시각을 제공하고, 주요 초점 영역을 식별하며, 추가 탐색이 가능한 영역을 가리키는 것을 목표로 합니다. Github: https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy.

CCS 개념: $\cdot$ 컴퓨팅 방법론 $\rightarrow$ 컴퓨터 비전 작업; 자연어 생성; 기계 학습 접근법.

추가적인 주요 단어 및 구절: 생성 모델(Generative Models), 확산 모델(Diffusion Models), 점수 기반 생성 모델(Score-Based Generative Models), 확률적 미분 방정식(Stochastic Differential Equations)

ACM 참조 형식:

Ling Yang, Zhilong Zhang, Yang Song, Shenda Hong, Runsheng Xu, Yue Zhao, Yingxia Shao, Wentao Zhang, Bin Cui, 그리고 MingHsuan Yang. 2022. 확산 모델: 방법론과 응용에 대한 종합적인 조사. 1, 1 (2022년 10월), 39페이지. https: //doi.org/XXXXXXX.XXXXXXX[^0]

1 서론(INTRODUCTION)

확산 모델(diffusion models) [90, 215, 220, 225]은 새로운 최첨단 딥 생성 모델(deep generative models)의 가족으로 부상했습니다. 이들은 이미지 합성(image synthesis)이라는 도전적인 작업에서 오랫동안 지속된 생성적 적대 신경망(generative adversarial networks, GANs) [73]의 우위를 깨뜨렸으며 $[49,90,220,225]$, 컴퓨터 비전(computer vision) $[2,9,17,20,91,93,115,118,137,151,161,174,200,202,245,267,268,282,289]$, 자연어 처리(natural language processing) [6, 96, 141, 207, 272], 시간 데이터 모델링(temporal data modeling) [1, 29, 126, 192, 230, 260], 멀티모달 모델링(multi-modal modeling) [7, 186, 198, 201, 287], 강인한 기계 학습(robust machine learning) $[16,24,114,240,270]$, 계산 화학(computational chemistry) $[3,94,107,133,135,153,256]$ 및 의료 영상 복원(medical image reconstruction) $[22,36-38,42,159,178,224,257]$과 같은 분야에서도 잠재력을 보여주었습니다.

확산 모델을 개선하기 위한 다양한 방법들이 개발되었으며, 이는 실증적 성능(empirical performance)을 향상시키는 것 $[166,217,221]$ 또는 이론적 관점에서 모델의 능력을 확장하는 것 [145, 146, 219, 225, 277]에 초점을 맞추고 있습니다. 지난 두 해 동안 확산 모델에 대한 연구 논문이 크게 증가하여, 새로운 연구자들이 이 분야의 최신 발전을 따라잡기가 점점 더 어려워지고 있습니다. 또한, 방대한 연구량은 주요 추세를 가리고 연구 진척을 방해할 수 있습니다. 이 서베이(survey)는 확산 모델 연구의 현재 상태에 대한 포괄적인 개요를 제공하고, 다양한 접근 방식을 분류하며, 주요 진보를 강조함으로써 이러한 문제들을 해결하고자 합니다. 우리는 이 서베이가 이 분야에 새로운 연구자들에게 유용한 입문점으로 작용하고, 경험 많은 연구자들에게는 더 넓은 관점을 제공하기를 바랍니다.

이 논문에서 우리는 먼저 확산 모델의 기초(fundations of diffusion models)를 설명합니다(섹션 2), 세 가지 주요한 형식인 노이즈 제거 확률 모델(denoising diffusion probabilistic models, DDPMs) [90, 215], 점수 기반 생성 모델(scorebased generative models, SGMs) [220, 221], 그리고 확률적 미분 방정식(stochastic differential equations, Score SDEs) [113, 219, 225]에 대한 간략하지만 독립적인 소개를 제공합니다. 이 모든 접근 방식의 핵심은 데이터를 점진적으로 강화되는 무작위 잡음(random noise)으로 교란하는 것(이른바 "확산" 과정이라고 함)입니다,

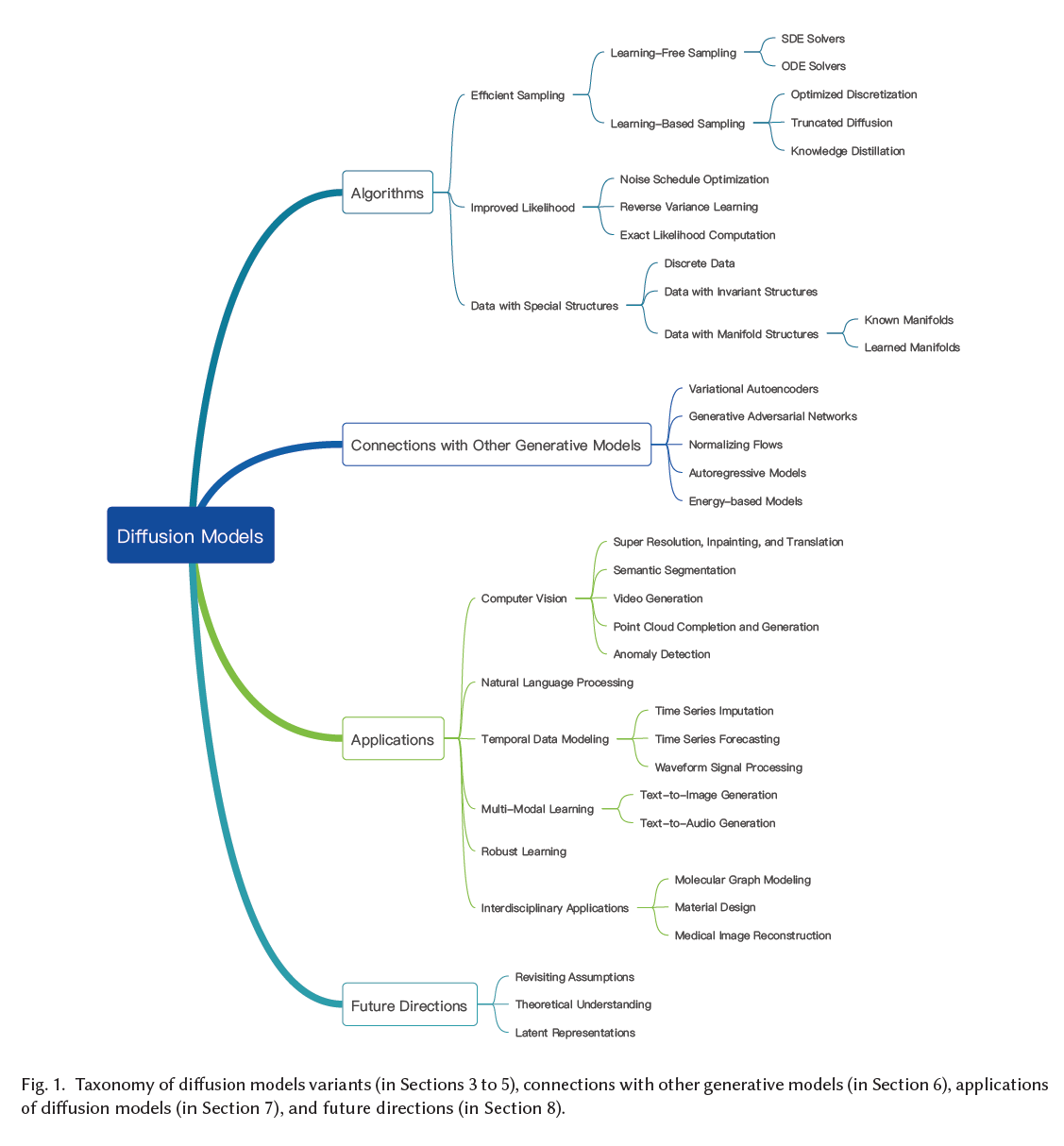
그림 1. 확산 모델 변형들의 분류(3~5절에서 다룸), 다른 생성 모델들과의 연결(6절에서 다룸), 확산 모델의 응용(7절에서 다룸), 그리고 미래 방향성(8절에서 다룸).

그런 다음 차례로 노이즈를 제거하여 새로운 데이터 샘플을 생성합니다. 우리는 이들이 확산의 동일한 원리 아래에서 어떻게 작동하는지 명확히 하고, 이 세 모델이 어떻게 연결되어 있으며 서로로 환원될 수 있는지 설명합니다.

다음으로, 우리는 확산 모델 분야를 매핑하여 최근 연구의 분류를 제시합니다. 이 분류는 효율적인 샘플링(3절), 개선된 가능도 추정(4절), 특수 구조를 가진 데이터 처리 방법(5절)의 세 가지 주요 영역으로 나눕니다. 여기에는 관계형 데이터, 순열/회전 불변성을 가진 데이터, 다양체 위에 있는 데이터 등이 포함됩니다. 우리는 각 범주를 더 세부적인 하위 범주로 나누어 모델을 검토합니다. 이는 ACM에 제출된 원고에서 그림으로 나타냈습니다.

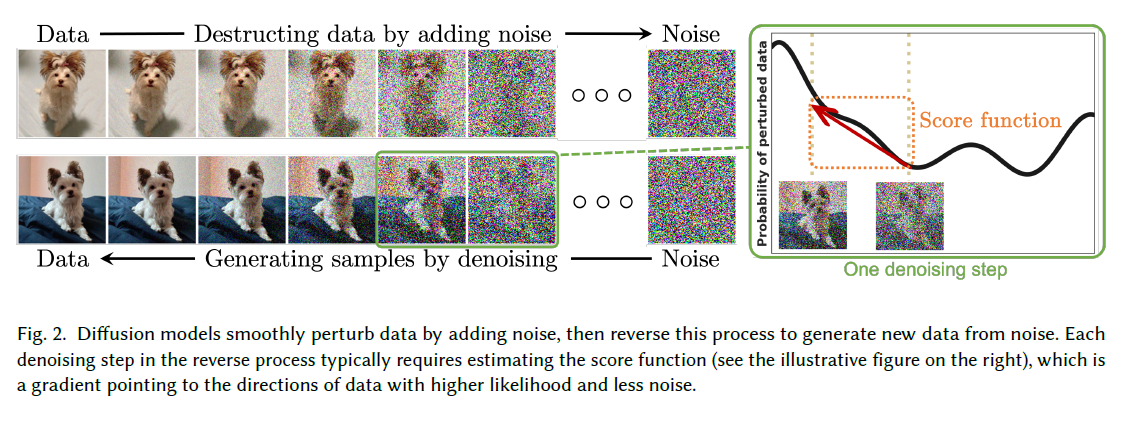
그림 2. 확산 모델은 데이터에 노이즈를 추가하여 부드럽게 변형시킨 다음, 이 과정을 역전시켜 노이즈로부터 새로운 데이터를 생성합니다. 역 과정에서의 각 제노이징(denoising) 단계는 일반적으로 점수 함수(score function)를 추정하는 것을 필요로 합니다(오른쪽에 있는 그림 참조). 이 함수는 가능성이 높고 노이즈가 적은 데이터 방향을 가리키는 그래디언트(gradient)입니다.

그림 1에서와 같이, 우리는 확산 모델과 다른 딥 생성 모델(deep generative models)과의 연결을 논의합니다(6절). 여기에는 변분 오토인코더(VAEs) [123, 195], 생성적 적대 신경망(GANs) [73], 정규화 플로우(normalizing flows) [50, 52, 175, 197], 자기회귀 모델(autoregressive models) [237], 에너지 기반 모델(EBMs) [132, 223]이 포함됩니다. 이러한 모델들을 확산 모델과 결합함으로써, 연구자들은 더 강력한 성능을 달성할 가능성을 가집니다.

이어서, 우리의 조사는 확산 모델이 기존 연구에서 적용된 여섯 가지 주요 응용 분야를 검토합니다(7절): 컴퓨터 비전, 자연어 처리, 시간 데이터 모델링, 멀티모달 학습, 강건한 학습, 그리고 학제간 응용. 각 작업에 대해 정의를 제공하고, 확산 모델이 그것을 해결하기 위해 어떻게 사용될 수 있는지 설명하며, 관련된 이전 작업을 요약합니다. 우리는 이 흥미로운 새 연구 분야의 가능한 미래 방향에 대한 전망을 제공하며 논문을 마무리합니다(8절과 9절).

2 확산 모델의 기초

확산 모델(diffusion models)은 데이터에 점진적으로 노이즈를 주입하여 데이터를 파괴하는 확률적 생성 모델의 한 가족으로, 이 과정을 역으로 학습하여 샘플을 생성합니다. 그림 2에서 확산 모델의 직관을 제시합니다. 현재 확산 모델에 대한 연구는 주로 세 가지 주요한 형식에 기반을 두고 있습니다: 노이즈 제거 확률적 모델(denoising diffusion probabilistic models, DDPMs) [90, 166, 215], 점수 기반 생성 모델(score-based generative models, SGMs) [220, 221], 그리고 확률적 미분 방정식(stochastic differential equations, Score SDEs) [219, 225]. 이 섹션에서는 이 세 가지 형식에 대한 자체 포함적인 소개를 제공하면서, 그들 사이의 연결에 대해 논의합니다.

2.1 노이즈 제거 확률적 모델(Denoising Diffusion Probabilistic Models, DDPMs)

노이즈 제거 확률적 모델(DDPM) [90,215]은 데이터를 노이즈로 변형시키는 전방향 마르코프 체인(forward chain)과 노이즈를 다시 데이터로 변환하는 역방향 마르코프 체인(reverse chain) 두 가지 마르코프 체인을 사용합니다. 전자는 일반적으로 어떤 데이터 분포도 간단한 사전 분포(예: 표준 가우시안)로 변환하는 목표로 수작업으로 설계되며, 후자의 마르코프 체인은 심층 신경망(deep neural networks)으로 매개변수화된 전이 커널(transition kernels)을 학습하여 전자를 역으로 합니다. 새로운 데이터 포인트는 사전 분포에서 무작위 벡터를 샘플링한 다음, 역방향 마르코프 체인을 통해 조상 샘플링(ancestral sampling)을 수행하여 생성됩니다 [125].

공식적으로, 데이터 분포 $\mathrm{x}_{0} \sim q\left(\mathrm{x}_{0}\right)$가 주어졌을 때, 전방향 마르코프 과정(Markov process)은 전이 커널 $q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$을 사용하여 무작위 변수 $\mathbf{x}_{1}, \mathbf{x}_{2} \ldots \mathbf{x}_{T}$의 시퀀스를 생성합니다. 확률의 연쇄 법칙(chain rule)과 마르코프 성질(Markov property)을 사용하여, $\mathbf{x}_{0}$에 조건을 둔 $\mathbf{x}_{1}, \mathbf{x}_{2} \ldots \mathbf{x}_{T}$의 결합 분포를 $q\left(\mathbf{x}_{1}, \ldots, \mathbf{x}_{T} \mid \mathbf{x}_{0}\right)$로 표시하고, 이를 다음과 같이 분해할 수 있습니다:

DDPMs에서는 데이터 분포 $q(\mathrm{x}_{0})$를 다루기 쉬운 사전 분포로 점진적으로 변환하기 위해 전이 커널 $q(\mathbf{x}_{t} \mid \mathbf{x}_{t-1})$을 직접 설계합니다. 전이 커널에 대한 전형적인 설계는 가우시안(Gaussian) 섭동이며, 가장 일반적인 전이 커널 선택은 다음과 같습니다.

여기서 $\beta_{t} \in(0,1)$는 모델 학습 전에 선택되는 하이퍼파라미터(hyperparameter)입니다. 우리는 여기서 논의를 단순화하기 위해 이 커널을 사용하지만, 다른 유형의 커널도 같은 방식으로 적용될 수 있습니다. Sohl-Dickstein et al. (2015) [215]에 의해 관찰된 바와 같이, 이 가우시안 전이 커널을 사용하면 식 (1)의 결합 분포를 주변화하여 모든 $t \in\{0,1, \cdots, T\}$에 대해 $q(\mathbf{x}_{t} \mid \mathbf{x}_{0})$의 분석적 형태를 얻을 수 있습니다. 구체적으로, $\alpha_{t}:=1-\beta_{t}$ 및 $\bar{\alpha}_{t}:=\prod_{s=0}^{t} \alpha_{s}$로 정의하면 다음과 같습니다.

$\mathrm{x}_{0}$이 주어지면, 가우시안 벡터 $\epsilon \sim \mathcal{N}(0, \mathrm{I})$을 샘플링하고 변환을 적용하여 $\mathrm{x}_{t}$의 샘플을 쉽게 얻을 수 있습니다.

$\bar{\alpha}_{T} \approx 0$일 때, $\mathbf{x}_{T}$는 거의 가우시안(Gaussian) 분포를 따르므로, 우리는 $q\left(\mathbf{x}_{T}\right):=\int q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right) q\left(\mathbf{x}_{0}\right) \mathrm{d} \mathbf{x}_{0} \approx \mathcal{N}\left(\mathbf{x}_{T} ; \mathbf{0}, \mathbf{I}\right)$라고 할 수 있습니다.

직관적으로 말하자면, 이 순방향 과정은 데이터에 천천히 노이즈(noise)를 주입하여 모든 구조가 사라질 때까지 진행됩니다. 새로운 데이터 샘플을 생성하기 위해, DDPMs(확률적 모델)는 먼저 사전 분포(prior distribution)에서 구조가 없는 노이즈 벡터를 생성합니다(이는 일반적으로 쉽게 얻을 수 있음), 그리고 역시간(reverse time) 방향으로 학습 가능한 마르코프 체인(Markov chain)을 실행하여 점차 노이즈를 제거합니다. 구체적으로, 역 마르코프 체인은 사전 분포 $p\left(\mathbf{x}_{T}\right)=\mathcal{N}\left(\mathbf{x}_{T} ; \mathbf{0}, \mathbf{I}\right)$와 학습 가능한 전이 커널(transition kernel) $p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$로 파라미터화됩니다. 순방향 과정이 $q\left(\mathbf{x}_{T}\right) \approx \mathcal{N}\left(\mathbf{x}_{T} ; \mathbf{0}, \mathbf{I}\right)$가 되도록 구성되기 때문에, 우리는 사전 분포 $p\left(\mathbf{x}_{T}\right)=\mathcal{N}\left(\mathbf{x}_{T} ; \mathbf{0}\right.$, I $)$를 선택합니다. 학습 가능한 전이 커널 $p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$은 다음과 같은 형태를 취합니다:

여기서 $\theta$는 모델 매개변수를 나타내며, 평균 $\mu_{\theta}\left(\mathbf{x}_{t}, t\right)$과 분산 $\Sigma_{\theta}\left(\mathbf{x}_{t}, t\right)$은 깊은 신경망(deep neural networks)에 의해 매개변수화됩니다. 이 역 마르코프 체인(reverse Markov chain)을 가지고 있으면, 먼저 잡음 벡터 $\mathbf{x}_{T} \sim p\left(\mathbf{x}_{T}\right)$를 샘플링한 다음, $t=1$이 될 때까지 학습 가능한 전이 커널(transition kernel) $\mathbf{x}_{t-1} \sim p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$에서 반복적으로 샘플링하여 데이터 샘플 $\mathbf{x}_{0}$을 생성할 수 있습니다.

이 샘플링 과정의 성공의 핵심은 역 마르코프 체인이 순방향 마르코프 체인(forward Markov chain)의 실제 시간 역전을 맞추도록 훈련하는 것입니다. 즉, 역 마르코프 체인의 결합 분포 $p_{\theta}\left(\mathbf{x}_{0}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{T}\right):=p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$가 순방향 과정의 분포 $q\left(\mathbf{x}_{0}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{T}\right):=q\left(\mathbf{x}_{0}\right) \prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$ (Eq. (1))에 가깝게 근사하도록 매개변수 $\theta$를 조정해야 합니다. 이는 두 분포 사이의 쿨백-라이블러(Kullback-Leibler, KL) 발산을 최소화함으로써 달성됩니다:

(i)는 KL 발산(KL divergence)의 정의에서, (ii)는 $q\left(\mathbf{x}_{0}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{T}\right)$와 $p_{\theta}\left(\mathbf{x}_{0}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{T}\right)$가 모두 분포의 곱이라는 사실에서, 그리고 (iii)는 젠센의 부등식(Jensen's inequality)에서 유래합니다. 식 (8)의 첫 번째 항은 데이터 $\mathbf{x}_{0}$의 로그 가능도(log-likelihood)의 변분 하한(variational lower bound, VLB)으로, 확률적 생성 모델(probabilistic generative models)을 훈련시키는 일반적인 목표입니다. "const"는 모델 매개변수 $\theta$에 의존하지 않는 상수를 나타내며, 따라서 최적화에 영향을 주지 않습니다. DDPM 훈련의 목표는 VLB를 최대화하는 것입니다(또는 동등하게, 부정적인 VLB를 최소화하는 것), 이는 독립적인 항들의 합이기 때문에 특히 최적화하기 쉽고, 몬테 카를로 샘플링(Monte Carlo sampling) [164]을 통해 효율적으로 추정하고, 확률적 최적화(stochastic optimization) [226]에 의해 효과적으로 최적화될 수 있습니다.

Ho et al. (2020) [90]은 $L_{\mathrm{VLB}}$의 여러 항을 재가중하여 샘플 품질을 향상시키고, 결과적인 손실 함수와 송과 어몬(Song and Ermon) [220]에서의 노이즈 조건 스코어 네트워크(noise-conditional score networks, NCSNs)의 훈련 목표 사이의 중요한 동등성을 발견했습니다. NCSNs는 점수 기반 생성 모델(score-based generative models)의 한 유형입니다. [90]에서의 손실은 다음과 같은 형태를 취합니다.

여기서 $\lambda(t)$는 양의 가중치 함수이고, $\mathbf{x}_{t}$는 식 (4)를 통해 $\mathbf{x}_{0}$와 $\epsilon$에서 계산되며, $\mathcal{U} \llbracket 1, T \rrbracket$는 집합 $\{1,2, \cdots, T\}$ 위의 균일 분포이고, $\epsilon_{\theta}$는 주어진 $\mathbf{x}_{t}$와 $t$에 대해 노이즈 벡터 $\epsilon$을 예측하는 매개변수 $\theta$를 가진 심층 신경망(deep neural network)입니다. 이 목적 함수는 가중치 함수 $\lambda(t)$의 특정 선택에 대해 식 (8)로 간소화되며, 다중 노이즈 스케일에 대한 노이즈 제거 점수 매칭(denoising score matching)의 손실 형태와 같으며, 이는 다음 섹션에서 논의될 확산 모델(diffusion models)의 또 다른 형식화입니다.

2.2 점수 기반 생성 모델(Score-Based Generative Models, SGMs)

점수 기반 생성 모델(Score-Based Generative Models, SGMs) [220, 221]의 핵심은 (Stein) 점수(score) (a.k.a., 점수 또는 점수 함수(score function)) [101] 개념입니다. 확률 밀도 함수(probability density function) $p(\mathbf{x})$가 주어졌을 때, 그 점수 함수는 로그 확률 밀도의 그래디언트 $\nabla_{\mathbf{x}} \log p(\mathbf{x})$로 정의됩니다. 통계에서 일반적으로 사용되는 Fisher 점수 $\nabla_{\theta} \log p_{\theta}(\mathbf{x})$와 달리, 여기서 고려되는 Stein 점수는 모델 매개변수 $\theta$가 아닌 데이터 $\mathbf{x}$의 함수입니다. 이는 확률 밀도 함수가 가장 크게 증가하는 방향을 가리키는 벡터 필드(vector field)입니다.

점수 기반 생성 모델(SGMs) [220]의 핵심 아이디어는 데이터에 일련의 강화되는 가우시안 노이즈(Gaussian noise)를 주입하고, 노이즈 수준에 따라 조건을 부여받은 심층 신경망 모델(deep neural network model)을 훈련시켜 모든 노이즈 데이터 분포에 대한 점수 함수를 공동으로 추정하는 것입니다(이를 [220]에서는 노이즈 조건부 점수 네트워크(Noise-Conditional Score Network, NCSN)라고 합니다). 샘플은 감소하는 노이즈 수준에서 점수 함수를 연결하여 점수 기반 샘플링 접근법을 사용하여 생성됩니다. 여기에는 Langevin Monte Carlo [81, 110, 176, 220, 225], 확률적 미분 방정식(Stochastic Differential Equations) [109, 225], 일반 미분 방정식(Ordinary Differential Equations) [113, 146, 219, 225, 277], 그리고 그들의 다양한 조합 [225]이 포함됩니다. 점수 기반 생성 모델의 형식화에서는 훈련과 샘플링이 완전히 분리되어 있으므로, 점수 함수의 추정 후 다양한 샘플링 기술을 사용할 수 있습니다.

2.1절에서와 유사한 표기법을 사용하여, $q\left(\mathbf{x}_{0}\right)$를 데이터 분포라 하고, $0<\sigma_{1}<\sigma_{2}<\cdots<\sigma_{t}<\cdots<\sigma_{T}$를 잡음 수준의 순서열이라 합니다. SGMs(점진적 생성 모델)의 전형적인 예는 데이터 포인트 $\mathbf{x}_{0}$에 가우시안 잡음 분포 $q\left(\mathrm{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathrm{x}_{t} ; \mathrm{x}_{0}, \sigma_{t}^{2} I\right)$를 더하여 $\mathbf{x}_{t}$로 변형시키는 것입니다. 이로 인해 잡음이 섞인 데이터 밀도의 순서열 $q\left(\mathrm{x}_{1}\right), q\left(\mathrm{x}_{2}\right), \cdots, q\left(\mathrm{x}_{T}\right)$가 생성되며, 여기서 $q\left(\mathrm{x}_{t}\right):=\int q\left(\mathrm{x}_{t}\right) q\left(\mathrm{x}_{0}\right) \mathrm{d} \mathbf{x}_{0}$입니다. 잡음 조건 스코어 네트워크(noise-conditional score network)는 깊은 신경망 $\mathbf{s}_{\theta}\left(\mathrm{x}_{,} t\right)$으로, 스코어 함수 $\nabla_{\mathbf{x}_{t}} \log q\left(\mathbf{x}_{t}\right)$를 추정하기 위해 훈련됩니다. 데이터로부터 스코어 함수를 학습하는 것(즉, 스코어 추정)은 스코어 매칭(score matching) [101], 노이즈 제거 스코어 매칭(denoising score matching) [188, 189, 238], 슬라이스 스코어 매칭(sliced score matching) [222]과 같은 확립된 기술들이 있으므로, 우리는 이들 중 하나를 직접 사용하여 잡음이 섞인 데이터 포인트로부터 잡음 조건 스코어 네트워크를 훈련할 수 있습니다. 예를 들어, 노이즈 제거 스코어 매칭을 사용하고 Eq. (10)에서와 유사한 표기법을 사용할 때, 훈련 목표는 다음과 같이 주어집니다:

(i)는 [238]에 의해 유도되었고, (ii)는 $q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathrm{N}\left(\mathbf{x}_{t} ; \mathbf{x}_{0}, \sigma_{t}^{2} \mathbf{I}\right)$라는 가정에서 나왔으며, (iii)는 $\mathbf{x}_{t}=\mathbf{x}_{0}+\sigma_{t} \epsilon$이라는 사실에서 나왔습니다. 다시 한번, 우리는 $\lambda(t)$를 양의 가중치 함수로, "const"를 훈련 가능한 매개변수 $\theta$에 의존하지 않는 상수로 표시합니다. 식 (14)와 식 (10)을 비교하면, DDPMs(Discrete Denoising Probabilistic Models)와 SGMs(Stochastic Gradient Methods)의 훈련 목표가 $\boldsymbol{\epsilon}_{\theta}(\mathrm{x}, t)=-\sigma_{t} \mathbf{s}_{\theta}(\mathrm{x}, t)$로 설정되면 동등함을 알 수 있습니다.

샘플 생성을 위해, SGMs는 반복적인 접근법을 사용하여 $\mathbf{s}_{\theta}(\mathbf{x}, T), \mathbf{s}_{\theta}(\mathbf{x}, T-1), \cdots, \mathbf{s}_{\theta}(\mathbf{x}, 0)$을 차례대로 생성합니다. SGMs에서 훈련과 추론의 분리로 인해 많은 샘플링 접근법이 존재하며, 그 중 일부는 다음 섹션에서 논의됩니다. 여기서 우리는 SGMs를 위한 첫 번째 샘플링 방법인 annealed Langevin dynamics(ALD) [220]를 소개합니다. 시간 단계당 반복 횟수를 $N$이라 하고, 스텝 크기를 $s_{t}>0$라 합니다. 우리는 먼저 ALD를 $\mathbf{x}_{T}^{(N)} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$로 초기화한 다음, $t=T, T-1, \cdots, 1$에 대해 차례로 Langevin Monte Carlo를 적용합니다. 각 시간 단계 $0 \leq t<T$에서, 우리는 $\mathbf{x}_{t}^{(0)}=\mathbf{x}_{t+1}^{(N)}$으로 시작한 후, $i=0,1, \cdots, N-1$에 대해 다음과 같은 업데이트 규칙에 따라 반복합니다:

랑주뱅 몬테카를로(Langevin Monte Carlo) [176] 이론은 $s_{t} \rightarrow 0$ 그리고 $N \rightarrow \infty$일 때, $\mathbf{x}_{0}^{(N)}$이 데이터 분포 $q\left(\mathrm{x}_{0}\right)$에서 유효한 샘플이 된다는 것을 보장합니다.

2.3 확률적 미분 방정식(스코어 SDEs)

DDPMs와 SGMs는 무한한 시간 단계 또는 노이즈 수준의 경우로 더 일반화될 수 있으며, 여기서 교란(perturbation)과 제거(denoising) 과정은 확률적 미분 방정식(SDEs)의 해(solution)입니다. 우리는 이 공식을 스코어 SDE [225]라고 부릅니다. 이는 노이즈 교란과 샘플 생성을 위해 SDEs를 활용하며, 제거 과정은 노이즈가 있는 데이터 분포의 스코어 함수를 추정하는 것을 요구합니다.

Manuscript submitted to ACM

스코어 SDEs는 다음과 같은 확률적 미분 방정식(SDE) [225]에 의해 지배되는 확산 과정을 통해 데이터를 노이즈로 교란합니다:

여기서 $\mathbf{f}(\mathbf{x}, t)$와 $g(t)$는 SDE의 확산(diffusion)과 드리프트(drift) 함수이며, $\mathbf{w}$는 표준 위너 과정(일명, 브라운 운동)입니다. DDPMs와 SGMs에서의 전방 과정(forward processes)은 이 SDE의 이산화(discretizations)입니다. Song et al. (2020) [225]에서 보여준 것처럼, DDPMs에 대응하는 SDE는 다음과 같습니다:

여기서 $\beta\left(\frac{t}{T}\right)=T \beta_{t}$는 $T$가 무한대로 갈 때입니다; 그리고 SGMs에 대응하는 SDE는 다음과 같이 주어집니다:

여기서 $\sigma\left(\frac{t}{T}\right)=\sigma_{t}$는 $T$가 무한대로 갈 때를 의미합니다. 여기서 $q_{t}(\mathbf{x})$는 전진 과정에서 $\mathbf{x}_{t}$의 분포를 나타내는 데 사용됩니다.

중요하게도, 식 (15)의 형태를 가진 어떤 확산 과정도 Anderson [4]에 의해 역시간 확산 방정식(SDE)을 풀어서 뒤집을 수 있다는 것이 증명되었습니다:

여기서 $\overline{\mathbf{w}}$는 시간이 거꾸로 흐를 때의 표준 위너 과정(Wiener process)이고, $\mathrm{d} t$는 무한히 작은 음의 시간 단계를 나타냅니다. 이 역시간 SDE의 해 경로는 전진 SDE의 해 경로와 동일한 주변 밀도를 공유하지만, 시간 방향이 반대로 진행됩니다 [225]. 직관적으로, 역시간 SDE의 해는 점차적으로 노이즈를 데이터로 변환하는 확산 과정입니다. 더욱이, Song et al. (2020) [225]은 역시간 SDE와 동일한 주변 분포를 가지는 경로를 가진 미분 방정식(ODE), 즉 확률 흐름 ODE의 존재를 증명합니다. 확률 흐름 ODE는 다음과 같이 주어집니다:

역시간 SDE와 확률 흐름 ODE 모두 동일한 데이터 분포에서 샘플링할 수 있게 해주며, 그들의 경로는 동일한 주변 분포를 가집니다.

각 시간 단계 $\mathrm{t}$에서의 점수 함수 $\nabla_{\mathbf{x}} \log q_{t}(\mathbf{x})$를 알게 되면, 역시간 SDE(방정식 (18))와 확률 흐름 ODE(방정식 (19))를 해제할 수 있으며, 이후에는 다양한 수치 기법을 사용하여 이를 풀어 샘플을 생성할 수 있습니다. 예를 들어, annealed Langevin dynamics [220] (cf., Section 2.2), 수치 SDE 해법들 [109, 225], 수치 ODE 해법들 [113, 146, 217, 225, 277], 그리고 예측-수정 방법들(MCMC와 수치 ODE/SDE 해법들의 조합) [225] 등이 있습니다. SGMs에서와 같이, 우리는 시간에 따라 변하는 점수 모델 $s_{\theta}\left(x_{t}, t\right)$를 파라미터화하여 방정식 (14)의 점수 매칭 목적을 연속 시간으로 일반화함으로써 점수 함수를 추정합니다. 이는 다음과 같은 목적으로 이어집니다:

여기서 $\mathcal{U}[0, T]$는 $[0, T]$ 구간에 대한 균등 분포를 나타내며, 나머지 표기법은 방정식 (14)를 따릅니다.

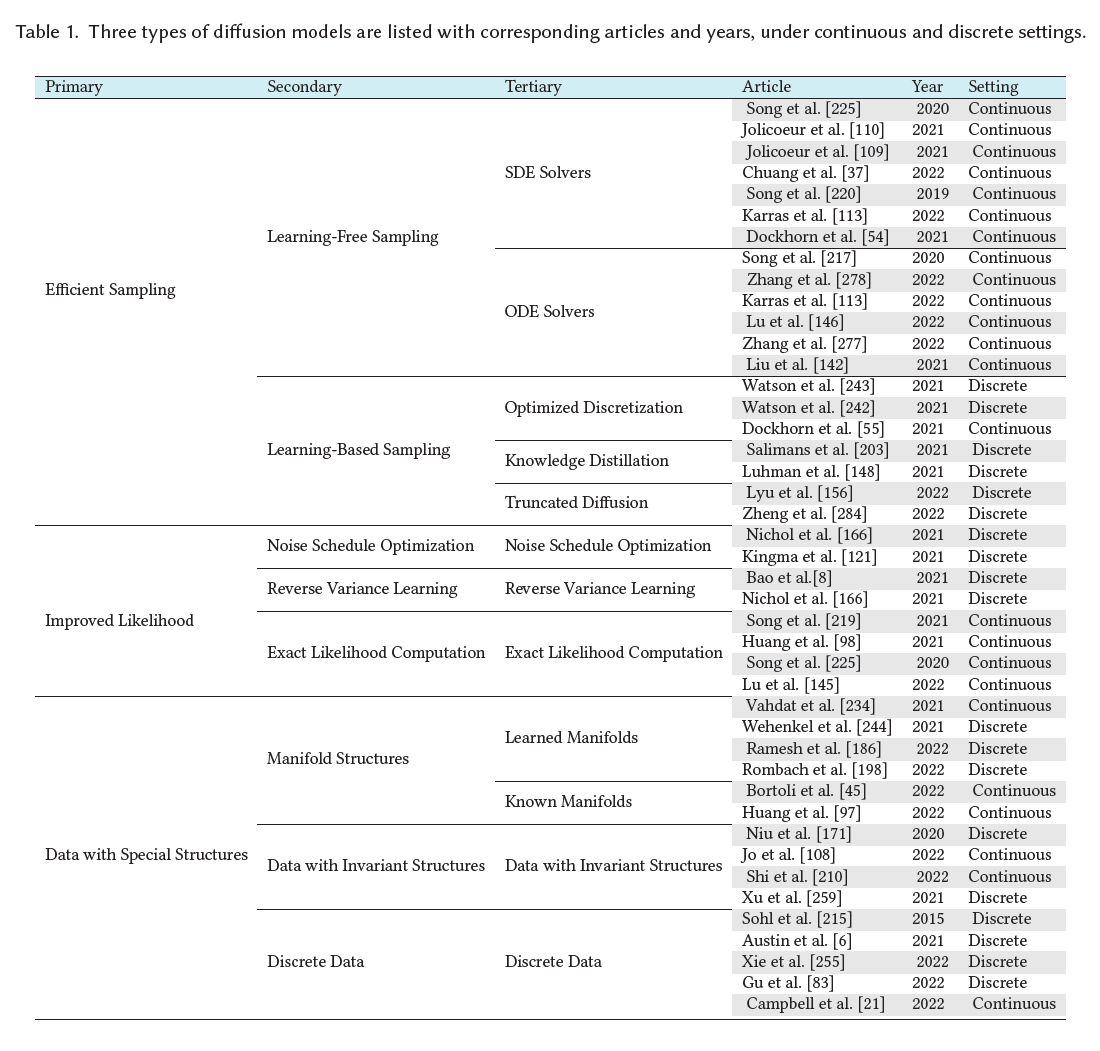
확산 모델에 대한 후속 연구는 세 가지 주요 방향에서 이러한 고전적 접근법(DDPMs, SGMs, 그리고 Score SDEs)을 개선하는 데 초점을 맞춥니다: 더 빠르고 효율적인 샘플링, 더 정확한 가능도 및 밀도 추정, 그리고 특별한 구조를 가진 데이터(예: 순열 불변성, 다양체 구조, 이산 데이터) 처리. 우리는 다음 세 섹션(섹션 3부터 5까지)에서 각 방향을 광범위하게 조사합니다. 표 1에서는 연속 및 이산 시간 설정하에 더 자세한 분류, 해당하는 문서들과 연도들을 포함하여 세 가지 유형의 확산 모델을 나열합니다.

표 1. 연속 및 이산 설정하에 해당하는 문서들과 연도들을 포함하여 세 가지 유형의 확산 모델이 나열됩니다.

3 효율적 샘플링을 가진 확산 모델들

확산 모델들로부터 샘플을 생성하는 것은 대체로 많은 수의 평가 단계를 포함하는 반복적인 접근법을 요구합니다. 최근의 많은 연구는 샘플링 과정을 가속화하면서도 결과 샘플의 품질을 향상시키는 데 집중하고 있습니다. 우리는 이러한 효율적인 샘플링 방법들을 크게 두 가지 주요 범주로 분류합니다: 학습이 필요 없는 샘플링(learning-free sampling)과 확산 모델이 훈련된 후 추가적인 학습 과정이 필요한 샘플링(learning-based sampling).

ACM에 제출된 원고

3.1 학습이 필요 없는 샘플링

많은 확산 모델 샘플러들은 식 (18)에 있는 역시간 SDE(reverse-time SDE)나 식 (19)의 확률 흐름 ODE(probability flow ODE)를 이산화하는 데 의존합니다. 샘플링 비용은 이산화된 시간 단계의 수에 비례하여 증가하기 때문에, 많은 연구자들은 시간 단계의 수를 줄이면서도 이산화 오류를 최소화하는 이산화 방식을 개발하는 데 집중하고 있습니다.

3.1.1 SDE 해결기. DDPM [90, 215]의 생성 과정은 역시간 SDE의 특정 이산화로 볼 수 있습니다. 2.3절에서 논의된 바와 같이, DDPM의 전방 과정은 식 (16)의 SDE를 이산화하며, 해당 역 SDE는 다음과 같은 형태를 취합니다.

Song et al. (2020) [225]은 식 (5)에 의해 정의된 역 마르코프 체인(reverse Markov chain)이 식 (21)의 수치적 SDE 해결기로서 기능한다는 것을 보여줍니다.

Noise-Conditional Score Networks(NCSNs) [220]와 Critically-Damped Langevin Diffusion(CLD) [54]은 모두 Langevin 동역학에서 영감을 받아 역시간 SDE를 해결합니다. 특히, NCSNs는 annealed Langevin dynamics(ALD, cf., Section 2.2)를 활용하여 데이터를 반복적으로 생성하면서 노이즈 수준을 부드럽게 줄여 최종적으로 생성된 데이터 분포가 원래 데이터 분포에 수렴하도록 합니다. ALD의 샘플링 궤적은 역시간 SDE의 정확한 해는 아니지만, 올바른 주변 분포(marginals)를 가지므로, Langevin 동역학이 모든 노이즈 수준에서 평형에 수렴한다는 가정 하에 올바른 샘플을 생성합니다. ALD 방법은 시간 단계의 더 나은 스케일링과 추가된 노이즈를 가진 score-based MCMC 접근법인 Consistent Annealed Sampling(CAS) [110]에 의해 더욱 개선되었습니다. 통계역학에서 영감을 받은 CLD는 보조 속도 항을 포함하는 확장된 SDE를 제안합니다. 이는 underdamped Langevin diffusion을 닮았습니다. 확장된 SDE의 시간 역전을 얻기 위해, CLD는 데이터에 대한 조건부 속도 분포의 score 함수만을 학습하면 되므로, 데이터의 score를 직접 학습하는 것보다 더 쉽다고 주장됩니다. 추가된 속도 항은 샘플링 속도와 품질을 향상시킨다고 보고되었습니다.

[225]에서 제안된 역 확산 방법은 역시간 SDE를 전진 SDE와 같은 방식으로 이산화합니다. 전진 SDE의 어떤 한 단계 이산화에 대해서, 아래와 같은 일반 형태를 쓸 수 있습니다:

여기서 $\mathbf{z}_{i} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), \mathbf{f}_{i}$와 $\mathbf{g}_{i}$는 SDE의 드리프트/확산 계수와 이산화 방식에 의해 결정됩니다. 역 확산은 역시간 SDE를 전진 SDE와 유사하게 이산화하도록 제안합니다. 즉,

여기서 $\mathbf{s}_{\theta^{*}}\left(\mathbf{x}_{i}, t_{i}\right)$는 훈련된 노이즈 조건부 점수 모델(noise-conditional score model)입니다. Song et al. (2020) [225]은 역 확산 방법(reverse diffusion method)이 식 (18)의 역시간 SDE(reverse-time SDE)에 대한 수치적 SDE 해결기(numerical SDE solver)임을 증명합니다. 이 과정은 어떤 종류의 전방 SDEs(forward SDEs)에도 적용될 수 있으며, 경험적 결과는 이 샘플러가 VP-SDE라고 불리는 특정 종류의 SDEs에 대해 DDPM [225]보다 약간 더 나은 성능을 보인다는 것을 나타냅니다.

Jolicoeur-Martineau et al. (2021) [109]은 더 빠른 생성을 위한 적응형 스텝 크기를 가진 SDE 해결기(SDE solver)를 개발합니다. 스텝 크기는 고차 SDE 해결기(high-order SDE solver)의 출력과 저차 SDE 해결기(low-order SDE solver)의 출력을 비교함으로써 제어됩니다. 각 시간 단계에서, 고차 및 저차 해결기는 각각 이전 샘플 $\mathbf{x}_{\text {prev }}^{\prime}$로부터 새로운 샘플 $\mathbf{x}_{\text {high }}^{\prime}$와 $\mathbf{x}_{\text {low }}^{\prime}$를 생성합니다. 그런 다음 두 샘플 간의 차이를 비교하여 스텝 크기를 조정합니다. 만약 $\mathbf{x}_{\text {high }}^{\prime}$와 $\mathbf{x}_{\text {low }}^{\prime}$가 유사하다면, 알고리즘은 $\mathbf{x}_{\text {high }}^{\prime}$를 반환하고 스텝 크기를 증가시킵니다. $\mathbf{x}_{\text {high }}^{\prime}$와 $\mathbf{x}_{\text {low }}^{\prime}$ 사이의 유사성은 다음과 같이 측정됩니다:

여기서 $\delta\left(\mathrm{x}_{\mathrm{low}}^{\prime}, \mathrm{x}_{\mathrm{prev}}^{\prime}\right):=\max \left(\epsilon_{a b s}, \epsilon_{\text {rel }} \max \left(\left|\mathrm{x}_{\text {low }}^{\prime},\right| \mathrm{x}_{\mathrm{prev}}^{\prime} \mid\right)\right)$이며, $\epsilon_{a b s}$와 $\epsilon_{\text {rel }}$은 절대 허용 오차(absolute tolerance)와 상대 허용 오차(relative tolerance)입니다.

[225]에서 제안된 예측자-수정자(predictor-corrector) 방법은 수치적인 SDE 해결기("예측자")와 반복적인 마르코프 체인 몬테 카를로(Markov chain Monte Carlo, MCMC) 접근법("수정자")을 결합하여 역 SDE를 해결합니다. 각 시간 단계에서, 예측자-수정자 방법은 먼저 수치적인 SDE 해결기를 사용하여 대략적인 샘플을 생성한 다음, 점수 기반 MCMC(score-based MCMC)를 사용하는 "수정자"가 샘플의 주변 분포를 수정합니다. 결과적으로 생성된 샘플들은 역시간 SDE의 해결 궤적과 동일한 시간-주변(time-marginals)을 가지며, 즉 모든 시간 단계에서 분포상 동등합니다. 경험적 결과는 랑제뱅 몬테 카를로(Langevin Monte Carlo)를 기반으로 한 수정자를 추가하는 것이 수정자 없이 추가적인 예측자를 사용하는 것보다 더 효율적임을 보여줍니다 [225]. Karras 등(2022) [113]은 [225]에서 랑제뱅 동역학 수정자를 개선하여 소음을 추가하고 제거하는 랑제뱅과 유사한 "churn" 단계를 제안함으로써 CIFAR-10 [128]과 ImageNet-64 [47]와 같은 데이터셋에서 새로운 최고의 샘플 품질을 달성했습니다.

3.1.2 ODE 해결기. 더 빠른 확산 샘플러에 대한 많은 연구는 2.3절에서 소개된 확률 흐름 ODE(방정식 (19))를 해결하는 것을 기반으로 합니다. SDE 해결기와 달리, ODE 해결기의 궤적은 결정론적이므로 확률적 변동의 영향을 받지 않습니다. 이러한 결정론적 ODE 해결기는 일반적으로 그 확률론적 대응물보다 훨씬 빠르게 수렴하지만, 약간 떨어지는 샘플 품질을 감수해야 합니다.

Denoising Diffusion Implicit Models(DDIM) [217]은 확산 모델 샘플링을 가속화하는 초기 작업 중 하나입니다. 원래의 동기는 다음과 같은 마르코프 체인을 가진 비마르코프(non-Markovian) 사례로 원래의 DDPM을 확장하는 것이었습니다

이 수식은 DDPM과 DDIM을 특별한 경우로 포함하고 있으며, 여기서 DDPM은 $\sigma_{t}^{2}=\frac{\hat{\beta}_{t-1}}{\hat{\beta}_{t}} \beta_{t}$로 설정하는 것에 해당하고, DDIM은 $\sigma_{t}^{2}=0$으로 설정하는 것에 해당합니다. DDIM은 이 비마르코프(Markov) 섭동 과정을 역으로 진행하는 마르코프 체인을 학습하며, $\sigma_{t}^{2}=0$일 때 완전히 결정론적입니다. $[113,146,203,217]$에서 DDIM 샘플링 과정은 확률 흐름 ODE의 특별한 이산화(discretization) 방식으로 나타난다는 것이 관찰되었습니다. 단일 데이터셋에 대한 DDIM의 분석에 영감을 받아, 일반화된 Denoising Diffusion Implicit Models (gDDIM) [278]은 Critically-Damped Langevin Diffusion (CLD) [54]과 같은 더 일반적인 확산 과정에 대해 결정론적 샘플링을 가능하게 하는 점수 네트워크(score network)의 수정된 매개변수화를 제안합니다. PNDM [142]은 $\mathcal{R}^{N}$에서 특정 다양체(manifold)를 따라 샘플을 생성하는 의사 수치 방법(pseudo numerical method)을 제안합니다. 이 방법은 비선형 전달 부분이 있는 수치 해석기(numerical solver)를 사용하여 다양체 위의 미분 방정식을 풀고 샘플을 생성하는데, 이는 DDIM을 특별한 경우로 포함하고 있습니다.

Karras et al. (2022) [113]의 광범위한 실험적 조사를 통해, Heun의 $2^{\text{nd}}$ order method [5]가 샘플 품질과 샘플링 속도 사이에서 훌륭한 절충을 제공한다는 것을 보여줍니다. 고차 해법(higher-order solver)은 학습된 점수 함수(score function)를 시간 단계마다 한 번 더 평가하는 비용으로 더 작은 이산화 오류(discretization error)를 초래합니다. Heun의 방법은 Euler의 방법보다 적은 샘플링 단계로 비슷하거나 더 나은 품질의 샘플을 생성합니다.

확산 지수 적분기 샘플러(Diffusion Exponential Integrator Sampler) [277]와 DPM-solver [146]는 확률 흐름 ODE(probability flow ODE)의 반선형 구조(semi-linear structure)를 활용하여 일반적인 Runge-Kutta 방법보다 더 효율적인 맞춤형 ODE 해법을 개발합니다. 특히, 확률 흐름 ODE의 선형 부분은 해석적으로 계산될 수 있으며, 비선형 부분은 ODE 해법 분야의 지수 적분기(exponential integrators)와 유사한 기술로 해결될 수 있습니다. 이 방법들은 DDIM을 1차 근사로 포함하지만, 단 10에서 20회의 반복으로 고품질 샘플을 생성할 수 있는 고차 적분기를 허용합니다. 이는 가속화된 샘플링 없이 확산 모델이 일반적으로 요구하는 수백 번의 반복보다 훨씬 적습니다.

3.2 학습 기반 샘플링

학습 기반 샘플링(Learning-based sampling)은 확산 모델에 대한 또 다른 효율적인 접근 방식입니다. 부분 단계를 사용하거나 역 과정에 대한 샘플러를 훈련함으로써, 이 방법은 샘플 품질의 약간의 저하를 감수하면서 더 빠른 샘플링 속도를 달성합니다. 수작업으로 만든 단계를 사용하는 학습 없는 접근법과 달리, 학습 기반 샘플링은 일반적으로 특정 학습 목표를 최적화하여 단계를 선택하는 것을 포함합니다.

3.2.1 최적화된 이산화. 사전 훈련된 확산 모델이 주어진 상태에서, Watson et al. (2021) [243]은 DDPMs의 훈련 목표를 극대화하기 위해 최적의 $K$ 시간 단계를 선택하는 최적의 이산화 방식을 찾는 전략을 제시합니다. 이 접근법의 핵심은 DDPM 목표를 개별 항목의 합으로 분해할 수 있다는 관찰에 있으며, 이는 동적 프로그래밍(dynamic programming)에 적합합니다. 그러나 DDPM 훈련에 사용되는 변분 하한(variational lower bound)이 샘플 품질과 직접적으로 상관관계가 없다는 것은 잘 알려져 있습니다 [232]. 이 문제를 해결하기 위해, Differentiable Diffusion Sampler Search [242]라는 후속 연구는 샘플 품질에 대한 일반적인 지표인 Kernel Inception Distance (KID) [15]를 직접 최적화합니다. 이 최적화는 재매개변수화(reparameterization) [123, 195]와 그래디언트 리마테리얼라이제이션(gradient rematerialization)의 도움으로 가능합니다. Dockhorn et al. (2022) [55]은 1차 점수 네트워크 위에 추가적인 헤드를 훈련함으로써 합성을 가속화하기 위한 2차 해법을 유도하는데, 이는 절단된 Taylor 방법(truncated Taylor methods)을 기반으로 합니다.

3.2.2 절단 확산(Truncated Diffusion)

확산 과정을 절단함으로써 샘플링 속도를 향상시킬 수 있습니다 $[156,284]$. 핵심 아이디어는 전방 확산 과정을 조기에 중단하고, 몇 단계만 진행한 후에 비가우시안(non-Gaussian) 분포를 가진 상태에서 역방향의 제거 노이즈 과정을 시작하는 것입니다. 이 분포로부터의 샘플은 변분 오토인코더(variational autoencoders) [123, 195]나 생성적 적대 신경망(generative adversarial networks) [73]과 같은 사전 훈련된 생성 모델로부터의 샘플을 확산시켜 효율적으로 얻을 수 있습니다.

3.2.3 지식 증류(Knowledge Distillation)

지식 증류를 사용하는 접근법은 확산 모델의 샘플링 속도를 상당히 향상시킬 수 있습니다 $[148,203]$. 구체적으로, Progressive Distillation [203]에서 저자들은 전체 샘플링 과정을 절반의 단계만 필요로 하는 더 빠른 샘플러로 증류하는 것을 제안합니다. 새로운 샘플러를 심층 신경망(deep neural network)으로 파라미터화함으로써, 저자들은 DDIM 샘플링 과정의 입력과 출력을 일치시키도록 샘플러를 훈련할 수 있습니다. 이 절차를 반복함으로써 샘플링 단계를 더 줄일 수 있지만, 단계가 적어질수록 샘플 품질이 저하될 수 있습니다. 이 문제를 해결하기 위해, 저자들은 확산 모델에 대한 새로운 파라미터화와 목적 함수에 대한 새로운 가중치 체계를 제안합니다.

4 개선된 가능도를 가진 확산 모델(DIFFUSION MODELS WITH IMPROVED LIKELIHOOD)

2.1절에서 논의한 바와 같이, 확산 모델의 훈련 목표는 로그 가능도(log-likelihood)에 대한 (음의) 변분 하한(variational lower bound, VLB)입니다. 그러나 이 하한은 많은 경우에 타이트하지 않을 수 있으며 $[121]$, 이로 인해 확산 모델로부터의 잠재적으로 최적이 아닌 로그 가능도가 발생할 수 있습니다. 이 절에서는 확산 모델에 대한 가능도 최대화를 위한 최근 연구를 살펴봅니다. 우리는 노이즈 일정 최적화(noise schedule optimization), 역방향 분산 학습(reverse variance learning), 그리고 정확한 로그 가능도 평가(exact loglikelihood evaluation) 세 가지 유형의 방법에 초점을 맞춥니다.

4.1 노이즈 일정 최적화(Noise Schedule Optimization)

확산 모델의 고전적인 형식에서는 전방 과정의 노이즈 일정이 훈련 가능한 파라미터 없이 수작업으로 만들어집니다. 확산 모델의 다른 파라미터와 함께 전방 노이즈 일정을 최적화함으로써 VLB를 더욱 극대화하여 더 높은 로그 가능도 값을 달성할 수 있습니다 $[121, 166]$.

iDDPM의 연구 $[166]$는 특정한 코사인 노이즈 일정(cosine noise schedule)이 로그 가능도를 향상시킬 수 있음을 보여줍니다. 특히, 그들의 연구에서 코사인 노이즈 일정은 다음과 같은 형태를 취합니다.

$\bar{\alpha}_{t}$와 $\beta_{t}$는 식(2)와 식(3)에서 정의되며, $m$은 $t=0$에서의 노이즈 규모를 조절하는 하이퍼파라미터(hyperparameter)입니다. 또한, 로그 영역(log domain)에서 $\beta_{t}$와 $1-\bar{\alpha}_{t}$ 사이의 보간을 통해 역분산(reverse variance)의 파라미터화를 제안합니다.

변분 확산 모델(Variational Diffusion Models, VDMs) [121]에서, 저자들은 노이즈 일정과 다른 확산 모델 매개변수를 공동으로 학습하여 연속 시간 확산 모델의 가능도(likelihood)를 향상시키는 것을 제안합니다. 이들은 단조 신경망(monotonic neural network) $\gamma_{\eta}(t)$을 사용하여 노이즈 일정을 파라미터화하고, $\sigma_{t}^{2}=\operatorname{sigmoid}\left(\gamma_{\eta}(t)\right), q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\bar{\alpha}_{t} \mathbf{x}_{0}, \sigma_{t}^{2} \mathbf{I}\right)$, 그리고 $\bar{\alpha}_{t}=\sqrt{\left(1-\sigma_{t}^{2}\right)}$에 따라 전방 교란 과정(forward perturbation process)을 구축합니다. 더욱이, 저자들은 데이터 포인트 $\mathbf{x}$에 대한 VLB(Variational Lower Bound)를 신호 대 잡음비(signal-to-noise ratio) $\mathrm{R}(t):=\frac{\bar{\alpha}_{t}^{2}}{\sigma_{t}^{2}}$에만 의존하는 형태로 단순화할 수 있음을 증명합니다. 특히, $L_{V L B}$는 다음과 같이 분해될 수 있습니다:

여기서 첫 번째와 두 번째 항은 변분 오토인코더(variational autoencoders) 학습에 비유하여 직접 최적화할 수 있습니다. 세 번째 항은 다음과 같이 더 단순화될 수 있습니다:

여기서 $\mathrm{R}_{\max }=R(1), \mathrm{R}_{\min }=R(T), \mathbf{x}_{v}=\bar{\alpha}_{v} \mathbf{x}_{0}+\sigma_{v} \epsilon$는 $\mathbf{x}_{0}$를 $t=R^{-1}(v)$까지 전방 퍼티베이션(forward perturbation) 과정을 통해 확산시켜 얻은 노이즈가 있는 데이터 포인트를 나타내고, $\tilde{\mathbf{x}}_{\theta}$는 확산 모델에 의해 예측된 노이즈가 없는 데이터 포인트를 나타냅니다. 결과적으로, 노이즈 스케줄은 $R_{\min}$과 $R_{\max}$에서 같은 값을 공유하는 한 VLB에 영향을 주지 않으며, VLB에 대한 몬테카를로 추정자(Monte Carlo estimators)의 분산에만 영향을 줍니다.

4.2 역 분산 학습(Reverse Variance Learning)

전통적인 확산 모델의 공식화는 역 마르코프 체인(reverse Markov chain)의 가우시안 전이 커널(Gaussian transition kernels)이 고정된 분산 매개변수를 가진다고 가정합니다. 우리가 식 (5)에서 역 커널을 $q_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}\left(\mu_{\theta}\left(\mathbf{x}_{t}, t\right), \Sigma_{\theta}\left(\mathbf{x}_{t}, t\right)\right)$로 공식화했지만, 종종 역 분산 $\Sigma_{\theta}\left(\mathbf{x}_{t}, t\right)$을 $\beta_{t} \mathbf{I}$로 고정했습니다. 많은 방법들이 VLB와 로그 가능도(log-likelihood) 값을 더욱 극대화하기 위해 역 분산도 학습하도록 제안합니다.

iDDPM [166]에서 Nichol과 Dhariwal은 선형 보간(linear interpolation)의 형태로 역 분산을 매개변화하고 하이브리드 목적 함수(hybrid objective)를 사용하여 학습하도록 제안합니다. 이는 더 높은 로그 가능도와 샘플 품질을 잃지 않으면서 더 빠른 샘플링을 가능하게 합니다. 특히, 그들은 식 (5)에서 역 분산을 다음과 같이 매개변수화합니다:

ACM에 제출된 원고
여기서 $\tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t}$이고 $\theta$는 VLB를 극대화하기 위해 공동으로 학습됩니다. 이 간단한 매개변수화는 $\Sigma_{\theta}\left(\mathbf{x}_{t}, t\right)$의 더 복잡한 형태를 추정할 때 발생하는 불안정성을 피하고, 가능도 값을 향상시킨다고 보고되었습니다.

Analytic-DPM [8]은 사전 학습된 스코어 함수(score function)에서 최적의 역 분산을 얻을 수 있다는 놀라운 결과를 보여주며, 아래의 분석적 형태를 가집니다:

결과적으로, 사전 훈련된 점수 모델(score model)을 가지고 있다면, 최적의 역방향 분산(reverse variances)을 얻기 위해 첫 번째와 두 번째 순간을 추정할 수 있습니다. 이를 변분 하한(VLB)에 대입하면 더 타이트한 VLB와 더 높은 가능도 값을 얻을 수 있습니다.

4.3 정확한 가능도 계산

점수 SDE(Score SDE) [225] 공식에서는 다음과 같은 역방향 SDE를 풀어서 샘플을 생성합니다. 여기서 식 (18)의 $\nabla_{\mathbf{x}_{t}} \log p_{\theta}\left(\mathbf{x}_{t}, t\right)$는 학습된 노이즈-조건부 점수 모델 $\mathbf{s}_{\theta}\left(\mathbf{x}_{t}, t\right)$로 대체됩니다:

여기서 $p_{\theta}^{\text {sde }}$는 위 SDE를 풀어서 생성된 샘플의 분포를 나타내는 데 사용합니다. 또한 식 (19)의 확률 흐름 ODE(probability flow ODE)에 점수 모델을 대입하여 데이터를 생성할 수도 있습니다. 이는 다음과 같습니다:

마찬가지로, 우리는 이 ODE를 풀어서 생성된 샘플의 분포를 $p_{\theta}^{\text {ode }}$로 표시합니다. 신경 ODE(neural ODEs) [30]와 연속 정규화 흐름(continuous normalizing flows) [77]에 대한 이론은 $p_{\theta}^{\text {ode }}$를 정확하게 계산할 수 있지만 높은 계산 비용이 든다는 것을 나타냅니다. $p_{\theta}^{\text {sde }}$에 대해서는, 여러 동시 작업들 [98, 145, 219]이 효율적으로 계산 가능한 변분 하한(variational lower bound)이 존재한다는 것을 보여주고, 우리는 수정된 확산 손실(diffusion losses)을 사용하여 확산 모델(diffusion models)을 직접 훈련시켜 $p_{\theta}^{\text {sde }}$를 최대화할 수 있습니다.

구체적으로, Song et al. (2021) [219]은 특별한 가중치 함수(우도 가중치, likelihood weighting)를 사용하면, 점수 SDE(score SDEs)를 훈련하는 데 사용된 목적이 데이터에 대한 $p_{\theta}^{\text {sde }}$의 기대값을 암묵적으로 최대화한다는 것을 증명했습니다. 다음과 같이 나타낼 수 있습니다:

여기서 $\mathcal{L}\left(\theta ; g(\cdot)^{2}\right)$는 $\lambda(t)=g(t)^{2}$를 사용한 식 (20)의 점수 SDE 목적입니다. $\mathbf{D}_{K L}\left(q_{0} \| p_{\theta}^{\text {sde }}\right)=-\mathbb{E}_{q_{0}} \log \left(p_{\theta}^{\text {sde }}\right)+$ 상수이고, $\mathbf{D}_{K L}\left(q_{T} \| \pi\right)$는 상수이므로, $\mathcal{L}\left(\theta ; g(\cdot)^{2}\right)$로 훈련하는 것은 데이터에 대한 기대 음의 로그 우도(expected negative log-likelihood)인 $-\mathbb{E}_{q_{0}} \log \left(p_{\theta}^{\text {sde }}\right)$를 최소화하는 것과 같습니다. 더욱이, Song et al. (2021)과 Huang et al. (2021) [98, 219]은 $p_{\theta}^{\text {sde }}(\mathbf{x})$에 대한 다음과 같은 경계를 제공합니다:

여기서 $\mathcal{L}^{\prime}(\mathbf{x})$는 다음과 같이 정의됩니다:

식 (37)의 첫 번째 부분은 암시적 점수 매칭(implicit score matching) [101]을 연상시키며, 전체 경계는 몬테카를로 방법(Monte Carlo methods)으로 효율적으로 추정할 수 있습니다.

확률 흐름 ODE(probability flow ODE)는 신경 ODE(neural ODEs) 또는 연속 정규화 흐름(continuous normalizing flows)의 특별한 경우이므로, $\log p_{\theta}^{\text {ode }}$를 정확하게 계산하기 위해 해당 분야의 잘 정립된 접근 방식을 사용할 수 있습니다. 구체적으로 다음과 같습니다.

위의 일차원 적분은 수치 ODE 해법(numerical ODE solvers)과 스킬링-허친슨 추적 추정기(Skilling-Hutchinson trace estimator) [100, 214]를 사용하여 계산할 수 있습니다. 불행히도, 이 공식은 각 데이터 포인트 $\mathbf{x}_{0}$에 대해 비용이 많이 드는 ODE 해법을 호출해야 하므로 데이터에서 $p_{\theta}^{\text {ode }}$를 최대화하기 위해 직접 최적화할 수 없습니다. 위의 공식을 사용하여 직접 $p_{\theta}^{\text {ode }}$를 최대화하는 비용을 줄이기 위해, Song et al. (2021) [219]은 $p_{\theta}^{\text {ode }}$를 최대화하기 위한 대리로 $p_{\theta}^{\text {sde }}$의 변분 하한(variational lower bound)을 최대화할 것을 제안하였고, 이로 인해 ScoreFlows라고 불리는 확산 모델(diffusion models)의 가족이 등장하게 되었습니다.

Lu et al. (2022) [145]는 기본 스코어 매칭 손실 함수(score matching loss function)뿐만 아니라 그것의 고차 일반화(higher order generalizations)를 최소화하는 것을 제안하여 ScoreFlows를 더욱 개선하였습니다. 그들은 $\log p_{\theta}^{\text {ode }}$가 첫 번째, 두 번째, 그리고 세 번째 차 스코어 매칭 오류(score matching errors)로 제한될 수 있다는 것을 증명했습니다. 이 이론적 결과를 바탕으로, 저자들은 고차 스코어 매칭 손실(high order score matching losses)을 최소화하기 위한 효율적인 훈련 알고리즘을 추가로 제안하고 데이터에 대한 개선된 $p_{\theta}^{\text {ode }}$를 보고했습니다.

5 특수 구조를 가진 데이터를 위한 확산 모델

확산 모델(diffusion models)은 이미지와 오디오와 같은 데이터 영역에서 큰 성공을 거두었지만, 다른 모달리티(modalities)로 원활하게 전환되는 것은 아닙니다. 많은 중요한 데이터 영역은 확산 모델이 효과적으로 기능하기 위해 고려해야 할 특수한 구조를 가지고 있습니다. 예를 들어, 연속 데이터 영역에서만 정의된 스코어 함수(score functions)에 의존하는 모델이나, 데이터가 저차원 다양체(low dimensional manifolds)에 거주하는 경우 어려움이 발생할 수 있습니다. 이러한 도전에 대처하기 위해, 확산 모델은 다양한 방식으로 적응해야 합니다.

5.1 이산 데이터

대부분의 확산 모델은 연속 데이터 영역(continuous data domains)을 대상으로 하고 있습니다. 왜냐하면 DDPMs에서 사용되는 가우시안 노이즈(Gaussian noise) 교란은 이산 데이터(discrete data)에 자연스럽게 맞지 않고, SGMs와 Score SDEs가 요구하는 스코어 함수는 연속 데이터 영역에서만 정의되기 때문입니다. 이러한 어려움을 극복하기 위해, 여러 연구들 [6, 83, 96, 255]은 Sohl-Dickstein et al. (2015) [215]을 기반으로 고차원의 이산 데이터를 생성합니다. 구체적으로, VQ-Diffusion [83]은 가우시안 노이즈를 이산 데이터 공간에서의 랜덤 워크(random walk)나 랜덤 마스킹 작업(random masking operation)으로 대체합니다. 결과적으로 전방 과정(forward process)의 전이 커널(transition kernel)은 다음과 같은 형태를 취합니다.

여기서 $\mathbf{v}(\mathbf{x})$는 원-핫(one-hot) 열 벡터이고, $\mathbf{Q}_{t}$는 게으른 랜덤 워크(lazy random walk)의 전이 커널입니다. D3PM [6]은 흡수 상태 커널(absorbing state kernels) 또는 이산화된 가우시안 커널(discretized Gaussian kernels)로 전방 노이징 과정(forward noising process)을 구성하여 확산 모델에서 이산 데이터를 수용합니다. Campbell et al. (2022) [21]은 이산 확산 모델을 위한 첫 번째 연속 시간 프레임워크(continuous-time framework)를 제시합니다. 연속 시간 마르코프 체인(Continuous Time Markov Chains)을 활용하여, 그들은 이산 대응물보다 우수한 성능을 내는 효율적인 샘플러를 도출할 수 있었으며, 샘플 분포와 실제 데이터 분포 사이의 오차에 대한 이론적 분석을 제공합니다.

5.2 불변 구조를 가진 데이터

많은 중요한 도메인의 데이터는 불변의 구조를 가지고 있습니다. 예를 들어, 그래프는 순열 불변(permutation invariant)이며, 점 구름(point clouds)은 이동과 회전에 대해 불변입니다. 확산 모델(diffusion models)에서 이러한 불변성은 종종 무시되곤 하는데, 이는 최적이 아닌 성능으로 이어질 수 있습니다. 이 문제를 해결하기 위해, 몇몇 연구들 [45, 171]은 데이터의 불변성을 고려할 수 있는 능력을 확산 모델에 부여하자고 제안합니다.

Niu et al. (2020) [171]은 확산 모델을 사용한 순열 불변 그래프 생성 문제를 처음으로 다룹니다. 그들은 EDP-GNN이라고 불리는 순열 동등한 그래프 신경망(permutation equivariant graph neural network) [74, 208, 251]을 사용하여 잡음 조건의 점수 모델(noise-conditional score model)을 매개변수화함으로써 이를 달성합니다. GDSS [108]는 연속 시간 그래프 확산 과정(continuous-time graph diffusion process)을 제안함으로써 이 아이디어를 더 발전시킵니다. 이 과정은 노드와 엣지의 결합 분포를 확률 미분 방정식(stochastic differential equations, SDEs)의 체계를 통해 모델링하며, 순열 불변성을 보장하기 위해 메시지 전달 연산(message-passing operations)을 사용합니다.

마찬가지로, Shi et al. (2021) [210]과 Xu et al. (2022) [259]은 확산 모델이 이동과 회전에 대해 불변인 분자 구조(molecular conformations)를 생성할 수 있도록 합니다. 예를 들어, Xu et al. (2022) [259]은 불변한 사전 분포(invariant prior)로 시작하고 동등한 마르코프 커널(equivariant Markov kernels)로 진화하는 마르코프 체인(Markov chains)이 불변한 주변 분포(invariant marginal distribution)를 유도할 수 있음을 보여줍니다. 이는 분자 구조 생성에서 적절한 데이터 불변성을 강제하는 데 사용될 수 있습니다. 정식으로, $\mathcal{T}$를 회전이나 이동 연산으로 두고, $p\left(\mathbf{x}_{T}\right)=p\left(\mathcal{T}\left(\mathbf{x}_{T}\right)\right), p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=p_{\theta}\left(\mathcal{T}\left(\mathbf{x}_{t-1}\right) \mid \mathcal{T}\left(\mathbf{x}_{t}\right)\right)$라고 할 때, Xu et al. (2022) [259]은 샘플의 분포가 $\mathcal{T}$에 대해 불변임을 보장한다는 것, 즉 $p_{0}(\mathbf{x})=p_{0}(\mathcal{T}(\mathbf{x}))$임을 증명합니다. 결과적으로, 사전 분포와 전이 커널이 같은 불변성을 가진다면, 회전과 이동에 불변인 분자 구조를 생성하는 확산 모델을 구축할 수 있습니다.

5.3 다양체 구조를 가진 데이터

기계 학습(machine learning)에서 다양한 구조를 가진 데이터는 흔합니다. 다양체 가설(manifold hypothesis) [63]에 따르면, 자연 데이터는 종종 본질적인 차원이 낮은 다양체(manifolds)에 존재합니다. 또한, 많은 데이터 영역은 잘 알려진 다양체 구조를 가지고 있습니다. 예를 들어, 기후와 지구 데이터는 우리 행성의 모양이 구(sphere)이기 때문에 자연스럽게 구에 놓여 있습니다. 많은 연구들이 다양체 위의 데이터에 대한 확산 모델(diffusion models) 개발에 집중하고 있습니다. 우리는 이러한 연구들을 다양체가 알려져 있는지, 학습되는지에 따라 분류하고 아래에 대표적인 작업들을 소개합니다.

5.3.1 알려진 다양체(Known Manifolds). 최근 연구들은 다양한 알려진 다양체에 대한 점수 기반 확산 방정식(Score SDE) 공식을 확장했습니다. 이러한 적응은 신경 ODE(neural ODEs) [30]와 연속 정규화 흐름(continuous normalizing flows) [77]을 리만 다양체(Riemannian manifolds) [144, 158]로 일반화하는 것과 평행합니다. 이 모델들을 훈련하기 위해, 연구자들은 점수 매칭(score matching)과 점수 함수(score functions)를 리만 다양체에 맞게 적용했습니다.

리만 점수 기반 생성 모델(Riemannian Score-Based Generative Model, RSGM) [45]은 구(spheres)와 도넛 모양의 토러스(toruses)를 포함하여, 약간의 조건을 만족하는 다양한 다양체를 수용합니다. RSGM은 확산 모델을 콤팩트 리만 다양체(compact Riemannian manifolds)로 확장할 수 있다는 것을 보여줍니다. 이 모델은 또한 다양체에서의 확산을 역전하는 공식을 제공합니다. 내재적 관점에서, RSGM은 지오데식 랜덤 워크(Geodesic Random Walk)를 사용하여 리만 다양체에서의 샘플링 과정을 근사합니다. 이는 일반화된 제거 노이즈 점수 매칭 목표(generalized denoising score matching objective)로 훈련됩니다.

반면에, 리만 확산 모델(Riemannian Diffusion Model, RDM) [97]은 변분 프레임워크(variational framework)를 사용하여 연속 시간 확산 모델을 리만 다양체로 일반화합니다. RDM은 $\log$-우도의 변분 하한(variational lower bound, VLB)을 손실 함수로 사용합니다. RDM 모델의 저자들은 이 VLB를 최대화하는 것이 리만 점수 매칭 손실(Riemannian score-matching loss)을 최소화하는 것과 동등하다는 것을 보여주었습니다. RSGM과 달리, RDM은 외재적 관점을 취하며, 관련 리만 다양체가 더 높은 차원의 유클리드 공간(Euclidean space)에 내장되어 있다고 가정합니다.

5.3.2 학습된 다양체(Learned Manifolds). 다양체 가설(manifold hypothesis) [63]에 따르면, 대부분의 자연 데이터는 본질적인 차원이 현저하게 감소된 다양체 위에 놓여 있습니다. 따라서, 이러한 다양체를 식별하고 직접적으로 확산 모델을 훈련하는 것은 데이터 차원이 낮기 때문에 유리할 수 있습니다. 많은 최근 연구들은 이 아이디어를 바탕으로, 오토인코더(autoencoder)를 사용하여 데이터를 낮은 차원의 다양체로 압축한 다음, 이 잠재 공간(latent space)에서 확산 모델을 훈련하는 것으로 시작했습니다. 이 경우, 다양체는 오토인코더에 의해 암시적으로 정의되고 재구성 손실(reconstruction loss)을 통해 학습됩니다. 성공하기 위해서는 오토인코더와 확산 모델의 공동 훈련을 가능하게 하는 손실 함수를 설계하는 것이 중요합니다.

잠재 점수 기반 생성 모델(Latent Score-Based Generative Model, LSGM) [234]은 점수 기반 확산 모델(Score SDE diffusion model)과 변분 오토인코더(Variational Autoencoder, VAE) [123, 195]를 결합하여 공동 학습 문제를 해결하고자 합니다. 이 구성에서 확산 모델은 사전 분포(prior distribution) 학습을 담당합니다. LSGM의 저자들은 VAE의 증거 하한(evidence lower bound)과 확산 모델의 점수 매칭(score matching) 목표를 결합한 공동 학습 목표를 제안합니다. 이로 인해 데이터 로그 가능도(log-likelihood)에 대한 새로운 하한이 생성됩니다. 확산 모델을 잠재 공간(latent space) 내에 위치시킴으로써, LSGM은 기존 확산 모델보다 빠른 샘플 생성을 달성합니다. 또한, LSGM은 이산 데이터(discrete data)를 연속적인 잠재 코드(continuous latent codes)로 변환하여 관리할 수 있습니다.

잠재 확산 모델(Latent Diffusion Model, LDM) [198]은 오토인코더와 확산 모델을 함께 학습하는 대신 각 구성 요소를 별도로 다룹니다. 먼저, 오토인코더는 저차원 잠재 공간을 생성하기 위해 학습됩니다. 그 다음, 확산 모델은 잠재 코드를 생성하기 위해 학습됩니다. DALLE-2 [186]는 CLIP 이미지 임베딩 공간에서 확산 모델을 학습한 후, CLIP 이미지 임베딩을 기반으로 이미지를 생성하는 별도의 디코더를 학습하는 유사한 전략을 사용합니다.

6 다른 생성 모델들과의 연결

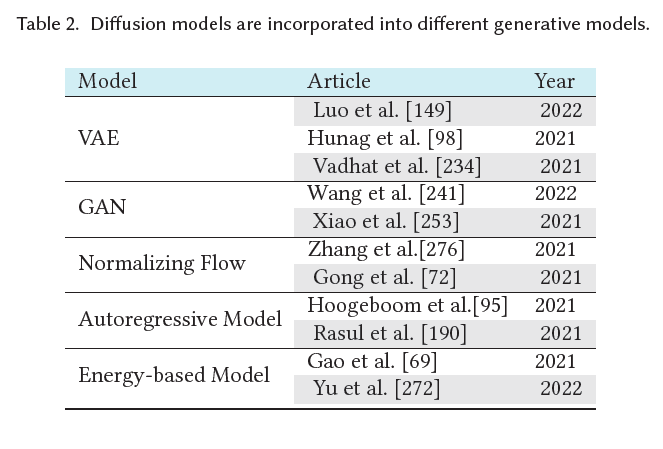
이 섹션에서는 먼저 다섯 가지 중요한 생성 모델 클래스를 소개하고 그들의 장점과 한계를 분석합니다. 그런 다음 확산 모델이 이들과 어떻게 연결되는지 소개하고, 확산 모델을 통합함으로써 이러한 생성 모델들이 어떻게 촉진되는지 설명합니다. 다른 생성 모델들과 확산 모델을 통합한 알고리즘은 표 2에 요약되어 있으며, 그림 3에서도 개략적인 설명을 제공합니다.

표 2. 다양한 생성 모델에 통합된 확산 모델들.

6.1 변분 오토인코더와 확산 모델과의 연결

변분 오토인코더(Variational Autoencoders) [56, 124, 195]는 연속적인 잠재 공간(latent space)에서 입력 데이터를 값으로 매핑하는 인코더(encoder)와 디코더(decoder)를 학습하는 것을 목표로 합니다. 이러한 모델에서, 임베딩(embedding)은 확률적 생성 모델(probabilistic generative model)에서 잠재 변수(latent variable)로 해석될 수 있으며, 매개변수화된 가능도 함수(parameterized likelihood function)에 의해 확률적 디코더(probabilistic decoder)가 구성될 수 있습니다. 또한, 데이터 $\mathbf{x}$는 관찰되지 않은 잠재 변수 $\mathbf{z}$에 의해 조건부 분포 $p_{\theta}(\mathbf{x} \mid \mathbf{z})$를 사용하여 생성된 것으로 가정됩니다.

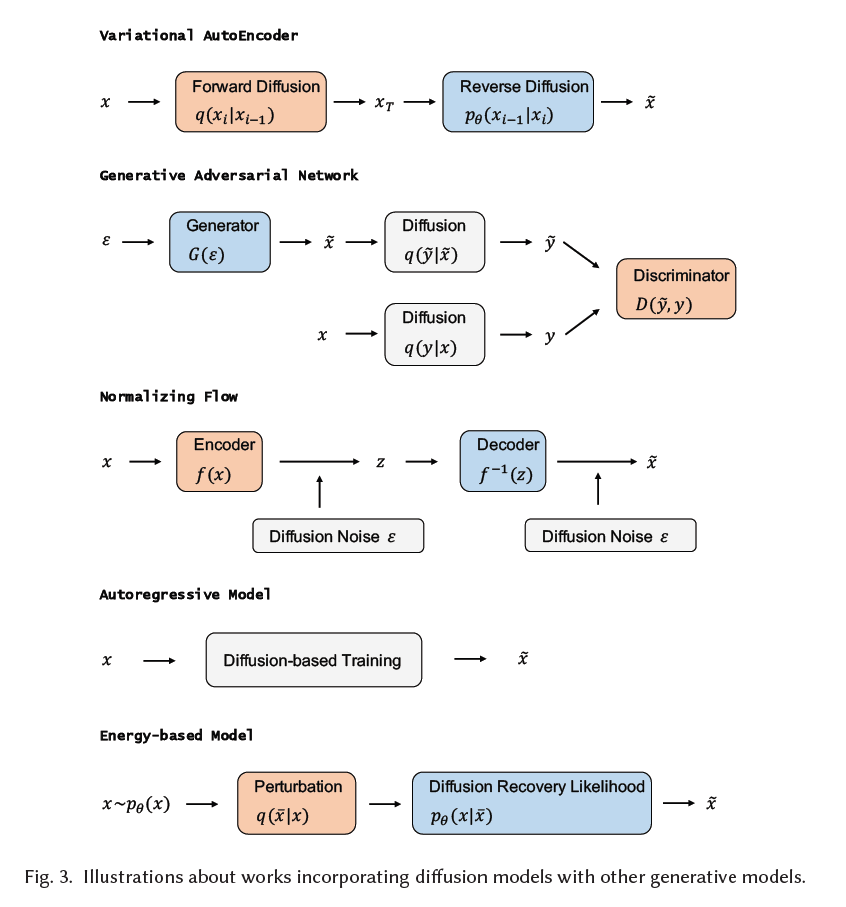
변분 오토인코더(Variational AutoEncoder)
생성적 적대 신경망(Generative Adversarial Network)
정규화 흐름(Normalizing Flow)
자기회귀 모델(Autoregressive Model)
에너지 기반 모델(Energy-based Model)

그림 3. 확산 모델(diffusion models)을 다른 생성 모델들과 통합하는 작업에 대한 일러스트레이션.

그리고 $q_{\phi}(\mathbf{z} \mid \mathbf{x})$는 $\mathbf{z}$를 근사적으로 추론하기 위해 사용됩니다. 효과적인 추론을 보장하기 위해, 변분 베이즈 접근법(variational Bayes approach)이 증거 하한(evidence lower bound)을 최대화하기 위해 사용됩니다:

$\mathcal{L}(\phi, \theta ; \mathbf{x}) \leq \log p_{\theta}(\mathbf{x})$를 만족할 때, 매개변수화된 가능도 함수(parameterized likelihood function) $p_{\theta}(\mathbf{x} \mid \mathbf{z})$와 매개변수화된 사후 근사(parameterized posterior approximation) $q_{\phi}(\mathbf{z} \mid \mathbf{x})$가 점별로 계산될 수 있고 그 매개변수에 대해 미분 가능하다면, ELBO(Evidence Lower Bound)는 경사 하강법(gradient descent)으로 최대화될 수 있습니다. 이 공식은 인코더(encoder)와 디코더(decoder) 모델의 유연한 선택을 가능하게 합니다. 일반적으로 이러한 모델들은 다층 신경망(multi-layer neural networks)에 의해 생성된 매개변수를 가진 지수 가족 분포(exponential family distributions)로 표현됩니다.

DDPM(Denoising Diffusion Probabilistic Models)은 고정된 인코더를 가진 계층적 마르코프 VAE(Variational Autoencoder)로 개념화될 수 있습니다. 구체적으로, DDPM의 순방향 과정은 인코더로 기능하며, 이 과정은 선형 가우시안 모델(linear Gaussian model)로 구조화되어 있습니다(식 (2)에 의해 설명됨). 반면에 DDPM의 역방향 과정은 디코더에 해당하며, 이는 여러 디코딩 단계에 걸쳐 공유됩니다. 디코더 내의 잠재 변수(latent variables)는 모두 샘플 데이터와 같은 크기입니다.

연속 시간 설정에서, Song et al. (2021) [225], Huang et al. (2021) [98], 그리고 Kingma et al. (2021) [121]은 스코어 매칭 목적(score matching objective)이 깊은 계층적 VAE의 ELBO로 근사될 수 있음을 보여줍니다. 따라서, 확산 모델(diffusion model)을 최적화하는 것은 무한히 깊은 계층적 VAE를 훈련하는 것으로 볼 수 있으며, 이는 Score SDE 확산 모델이 계층적 VAE의 연속적인 한계로 해석될 수 있다는 일반적인 믿음을 뒷받침하는 발견입니다.

잠재 스코어 기반 생성 모델(Latent Score-Based Generative Model, LSGM) [234]은 ELBO를 잠재 공간 확산(latent space diffusion)의 맥락에서 특수한 스코어 매칭 목적으로 간주할 수 있음을 보여주며 이 연구 분야를 더 발전시킵니다. ELBO의 교차 엔트로피 항(crossentropy term)은 다루기 어렵지만, 스코어 기반 생성 모델을 무한히 깊은 VAE로 보면, 다루기 쉬운 스코어 매칭 목적으로 변환될 수 있습니다.

6.2 생성적 적대 신경망(Generative Adversarial Networks)과 확산 모델과의 연결점

생성적 적대 신경망(Generative Adversarial Networks, GANs) $[40,73,84]$은 주로 생성기(generator) $G$와 판별기(discriminator) $D$ 두 모델로 구성됩니다. 이 두 모델은 일반적으로 신경망으로 구축되지만, 입력 데이터를 한 공간에서 다른 공간으로 매핑하는 어떤 형태의 미분 가능한 시스템으로도 구현될 수 있습니다. GAN의 최적화는 값 함수 $V(G, D)$를 가진 미니맥스(mini-max) 최적화 문제로 볼 수 있습니다:

생성기 $G$는 새로운 예시를 생성하고 데이터 분포를 암묵적으로 모델링하는 것을 목표로 합니다. 판별기 $D$는 보통 이진 분류기로, 생성된 예시와 실제 예시를 최대한 정확하게 식별하는 데 사용됩니다. 최적화 과정은 생성기에 대해 최소값을, 판별기에 대해 최대값을 생성하는 안장점(saddle point)에서 끝납니다. 즉, GAN 최적화의 목표는 나쉬 균형(Nash equilibrium) [193]을 달성하는 것입니다. 그 지점에서 생성기는 실제 예시의 정확한 분포를 포착했다고 간주할 수 있습니다.

GAN의 문제점 중 하나는 훈련 과정에서의 불안정성으로, 주로 입력 데이터의 분포와 생성된 데이터의 분포 사이에 중첩이 없기 때문에 발생합니다. 한 가지 해결책은 판별기 입력에 노이즈를 주입하여 생성기와 판별기 분포의 지지(support)를 넓히는 것입니다. 유연한 확산 모델(diffusion model)을 활용하여, Wang et al. (2022) [241]은 확산 모델에 의해 결정된 적응형 노이즈 일정을 판별기에 주입합니다. 반면에, GAN은 확산 모델의 샘플링 속도를 촉진할 수 있습니다. Xiao et al. (2021) [253]은 느린 샘플링이 제거 단계에서의 가우시안 가정에 의해 발생하는데, 이는 작은 단계 크기에 대해서만 정당화됩니다. 따라서, 각 제거 단계는 조건부 GAN(conditional GAN)으로 모델링되어 더 큰 단계 크기를 허용합니다.

6.3 정규화 흐름(Normalizing Flows)과 확산 모델과의 연결

노멀라이징 플로우(Normalizing flows) $[51,194]$는 고차원 데이터 $[53,122]$를 모델링하기 위해 다루기 쉬운 분포를 생성하는 생성 모델입니다. 노멀라이징 플로우는 단순한 확률 분포를 매우 복잡한 확률 분포로 변환할 수 있으며, 이는 생성 모델, 강화 학습(reinforcement learning), 변분 추론(variational inference) 및 기타 분야에서 사용될 수 있습니다. 기존의 노멀라이징 플로우는 변수 변환 공식(change of variable formula) [51, 194]을 기반으로 구축되었습니다. 노멀라이징 플로우에서의 궤적은 미분 방정식에 의해 정의됩니다. 이산 시간(discrete-time) 설정에서, 노멀라이징 플로우에서 데이터 $\mathbf{x}$에서 잠재 변수 $\mathrm{z}$로의 매핑은 일련의 전단사(bijections)의 합성으로 이루어지며, $F=F_{N} \circ F_{N-1} \circ \ldots \circ F_{1}$의 형태를 취합니다. 노멀라이징 플로우에서의 궤적 $\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots \mathbf{x}_{N}\right\}$은 다음을 만족합니다:

모든 $i \leq N$에 대하여.

연속적인 설정(continuous setting)과 유사하게, 노멀라이징 플로우는 변수 변환 공식을 통해 정확한 로그 가능도(log-likelihood)를 검색할 수 있습니다. 그러나, 전단사 요구 사항은 실제 및 이론적 맥락에서 복잡한 데이터 모델링을 제한합니다 [39, 246]. 몇몇 연구는 이 전단사 요구 사항을 완화하려고 시도합니다 [53, 246]. 예를 들어, DiffFlow [276]는 플로우 기반(flow-based) 모델과 확산 모델(diffusion models)의 장점을 결합한 생성 모델링 알고리즘을 소개합니다. 결과적으로, DiffFlow는 노멀라이징 플로우보다 더 선명한 경계를 생성하고, 확산 확률 모델(diffusion probabilistic models)에 비해 더 적은 이산화 단계로 더 일반적인 분포를 학습합니다.

6.4 자기회귀 모델(Autoregressive Models)과 확산 모델과의 연결

자기회귀 모델(Autoregressive Models, ARMs)은 확률 연쇄 규칙(probability chain rule)을 사용하여 데이터의 결합 분포(joint distribution)를 조건부 분포들의 곱으로 분해함으로써 작동합니다:

여기서 $\mathbf{x}_{<t}$는 $x_{1}, x_{2}, \ldots, x_{t-1}[11,130]$을 간략하게 나타낸 것입니다. 최근 딥 러닝(deep learning)의 발전은 이미지[34, 237], 오디오[112, 236], 텍스트[12, 18, 80, 160, 163]와 같은 다양한 데이터 형태에 대한 상당한 진전을 이루는 데 도움이 되었습니다. 자기회귀 모델(ARMs)은 단일 신경망을 사용하여 생성 능력을 제공합니다. 이 모델들로부터 샘플링하는 것은 데이터의 차원 수만큼 네트워크 호출을 필요로 합니다. ARMs는 효과적인 밀도 추정기이지만, 특히 고차원 데이터의 경우 샘플링은 연속적이고 시간이 많이 소요되는 과정입니다.

반면에 자기회귀 확산 모델(ARDM)[95]은 순서를 고려하지 않는 자기회귀 모델과 이산 확산 모델을 특별한 경우로 포함하여 임의 순서의 데이터를 생성할 수 있는 능력이 있습니다[6, 96, 216]. ARMs처럼 표현에 인과 마스킹(causal masking)을 사용하는 대신, ARDM은 확산 확률 모델의 목적을 반영하는 효과적인 목표로 훈련됩니다. 테스트 단계에서 ARDM은 데이터를 병렬로 생성할 수 있어 임의 생성 작업에 적용할 수 있습니다.

6.5 에너지 기반 모델과 확산 모델과의 연결

에너지 기반 모델(EBMs)[26, 48, 58, 64, 67, 68, 75, 78, 79, 120, 129, 132, 165, 170, 182, 196, 254, 281]은 판별자(discriminators)의 한 생성적 버전으로 볼 수 있으며 $[79,104,131,134]$ 레이블이 없는 입력 데이터로부터 학습될 수 있습니다. $\mathbf{x} \sim p_{\text {data }}(\mathbf{x})$가 훈련 예제를 나타내고, $p_{\theta}(\mathbf{x})$가 $p_{\text {data }}(\mathbf{x})$를 근사하려는 확률 밀도 함수를 나타낸다고 합시다. 에너지 기반 모델은 다음과 같이 정의됩니다:

여기서 $Z_{\theta}=\int \exp \left(f_{\theta}(\mathbf{x})\right) d \mathbf{x}$는 분할 함수(partition function)이며, 고차원 $\mathbf{x}$에 대해서는 해석적으로 다루기 어렵습니다. 이미지의 경우, $f_{\theta}(\mathrm{x})$는 스칼라 출력을 가진 합성곱 신경망(convolutional neural network)으로 파라미터화됩니다. Salimans 등(2021) [204]은 데이터 분포의 점수를 모델링하기 위해 제약이 있는 점수 모델(constrained score models)과 에너지 기반 모델(energy-based models)을 비교하였으며, 제약이 있는 점수 모델, 즉 에너지 기반 모델이 비교 가능한 모델 구조를 사용할 때 제약이 없는 모델(unconstrained models)만큼 잘 수행할 수 있다는 것을 발견했습니다.

EBM은 많은 바람직한 특성을 가지고 있지만, 고차원 데이터를 모델링할 때 두 가지 도전 과제가 남아 있습니다. 첫째, 우도(likelihood)를 최대화하여 EBM을 학습하는 것은 모델로부터 샘플을 생성하기 위해 MCMC 방법을 필요로 하며, 이는 매우 계산 비용이 많이 듭니다. 둘째, [169]에서 보여주듯이, 수렴하지 않는 MCMC로 학습된 에너지 포텐셜은 안정적이지 않습니다. 즉, 장기적인 마르코프 체인(Markov chains)으로부터의 샘플이 관찰된 샘플과 상당히 다를 수 있으며, 따라서 학습된 에너지 포텐셜을 평가하기 어렵습니다. 최근 연구에서 Gao 등(2021) [69]은 확산 모델의 역과정에서 일련의 EBM으로부터 샘플을 합리적으로 학습할 수 있는 확산 복구 우도(diffusion recovery likelihood) 방법을 제시했습니다. 각 EBM은 복구 우도(recovery likelihood)로 훈련되며, 이는 더 높은 노이즈 수준에서의 노이즈가 있는 버전들을 주어진 상태에서 특정 노이즈 수준에서 데이터의 조건부 확률을 최대화하는 것을 목표로 합니다. EBM은 조건부 분포로부터 샘플링하는 것이 주변 분포로부터 샘플링하는 것보다 훨씬 쉽기 때문에 복구 우도를 최대화합니다. 이 모델은 고품질의 샘플을 생성할 수 있으며, 조건부 분포로부터의 장기적인 MCMC 샘플은 여전히 현실적인 이미지와 유사합니다.

7 확산 모델의 응용 분야

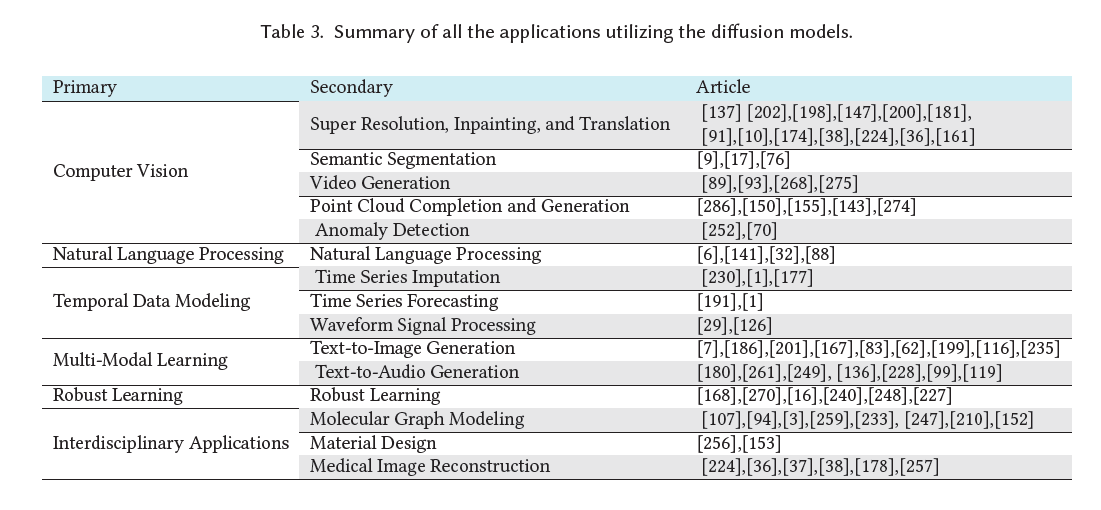
최근 확산 모델은 그들의 유연성과 강점으로 인해 다양한 도전적인 실제 세계 과제를 해결하기 위해 사용되었습니다. 우리는 과제에 따라 이러한 응용 분야를 컴퓨터 비전(computer vision), 자연어 처리(natural language processing), 시계열 데이터 모델링(temporal data modeling), 멀티모달 학습(multi-modal learning), 강건한 학습(robust learning), 그리고 학제간 응용(interdisciplinary applications)의 여섯 가지 다른 카테고리로 분류했습니다. 각 카테고리에 대해, 우리는 과제에 대한 간략한 소개와 확산 모델이 성능을 향상시키기 위해 어떻게 적용되었는지에 대한 자세한 설명을 제공합니다. 표 3은 확산 모델을 사용한 다양한 응용 분야를 요약하고 있습니다.

표 3. 확산 모델을 활용한 모든 응용 분야의 요약.

7.1 컴퓨터 비전(Computer Vision)

7.1.1 초해상도, 인페인팅, 변환(Super Resolution, Inpainting, and Translation). 생성 모델(generative models)은 초해상도(super-resolution), 인페인팅(inpainting), 변환(translation)을 포함한 다양한 이미지 복원 작업에 사용되었습니다 [10, 47, 61, 103, 137, 174, 187, 282]. 이미지 초해상도는 저해상도 입력으로부터 고해상도 이미지를 복원하는 것을 목표로 하며, 이미지 인페인팅은 이미지에서 누락되거나 손상된 영역을 재구성하는 것을 중심으로 합니다.

이러한 작업을 위해 확산 모델(diffusion models)을 사용하는 여러 방법이 있습니다. 예를 들어, 반복적인 정제를 통한 초해상도(Super-Resolution via Repeated Refinement, SR3) [202]는 조건부 이미지 생성을 가능하게 하는 DDPM을 사용합니다. SR3은 확률적이고 반복적인 제거 과정을 통해 초해상도를 수행합니다. 연속 확산 모델(Cascaded Diffusion Model, CDM) [91]은 점차 해상도를 높여가며 이미지를 생성하는 여러 확산 모델로 구성됩니다. SR3와 CDM 모두 입력 이미지에 직접 확산 과정을 적용하는데, 이로 인해 평가 단계가 더 커집니다.

제한된 컴퓨팅 자원으로 확산 모델(diffusion models)을 훈련할 수 있도록, 일부 방법들 [198, 234]은 사전 훈련된 오토인코더(autoencoders)를 사용하여 확산 과정을 잠재 공간(latent space)으로 전환하였습니다. 잠재 확산 모델(Latent Diffusion Model, LDM) [198]은 노이즈 제거(denoising) 확산 모델의 훈련과 샘플링 과정을 간소화하면서도 품질을 희생하지 않습니다.

이미지 복원(inpainting) 작업을 위해, RePaint [147]는 이미지를 더 잘 조절하기 위해 재샘플링 반복을 사용하는 개선된 노이즈 제거 전략을 특징으로 합니다(그림 Fig. 5 참조). 한편, Palette [200]는 조건부 확산 모델(conditional diffusion models)을 사용하여 색상화(colorization), 이미지 복원(inpainting), 이미지 확장(uncropping), JPEG 복원(JPEG restoration)의 네 가지 이미지 생성 작업을 위한 통합 프레임워크를 제공합니다.

이미지 변환(image translation)은 특정 원하는 스타일로 이미지를 합성하는 데 중점을 둡니다 [103]. SDEdit [161]는 확률적 미분 방정식(Stochastic Differential Equation, SDE) 사전 지식을 사용하여 충실도를 향상시킵니다. 구체적으로, 입력 이미지에 노이즈를 추가한 다음, SDE를 통해 이미지의 노이즈를 제거합니다.

그림 4. LDM [198]에 의해 생성된 이미지 초고해상도 결과.

그림 5. RePaint [147]에 의해 생성된 이미지 인페인팅 결과.

7.1.2 의미론적 분할(Semantic Segmentation). 의미론적 분할은 각 이미지 픽셀을 정해진 객체 카테고리에 따라 라벨링하는 것을 목표로 합니다. 생성적 사전 학습(generative pre-training)은 의미론적 분할 모델의 라벨 활용을 향상시킬 수 있으며, 최근 연구에서는 DDPM을 통해 학습된 표현이 분할 작업에 유용한 고수준 의미 정보를 포함하고 있다는 것을 보여주었습니다 $[9,76]$. 이러한 학습된 표현을 활용하는 소수샷 방법(few-shot method)은 VDVAE [33] 및 ALAE [179]와 같은 대안들을 능가하는 성능을 보였습니다. 마찬가지로, 디코더 디노이징 사전 학습(Decoder Denoising Pretraining, DDeP) [17]은 확산 모델(diffusion models)을 디노이징 오토인코더(denoising autoencoders) [239]와 통합하여 라벨 효율적인 의미론적 분할에 대해 유망한 결과를 제공합니다.

7.1.3 비디오 생성(Video Generation). 고품질 비디오를 생성하는 것은 비디오 프레임의 복잡성과 시공간 연속성 때문에 딥 러닝 시대에 여전히 도전적인 과제입니다 [265, 273]. 최근 연구는 생성된 비디오의 품질을 향상시키기 위해 확산 모델로 전환하고 있습니다 [93]. 예를 들어, 유연한 확산 모델(Flexible Diffusion Model, FDM) [89]은 주어진 다른 부분집합을 바탕으로 비디오 프레임의 임의의 부분집합을 샘플링할 수 있는 생성 모델을 사용합니다. FDM은 또한 이 목적을 위해 설계된 특화된 아키텍처를 포함합니다. 추가적으로, 잔차 비디오 확산(Residual Video Diffusion, RVD) 모델 [268]은 자기회귀적인, 엔드-투-엔드 최적화된 비디오 확산 모델을 활용합니다. 이 모델은 역 확산 과정을 통해 생성된 확률적 잔차를 사용하여 결정론적인 다음 프레임 예측을 수정함으로써 미래 프레임을 생성합니다.

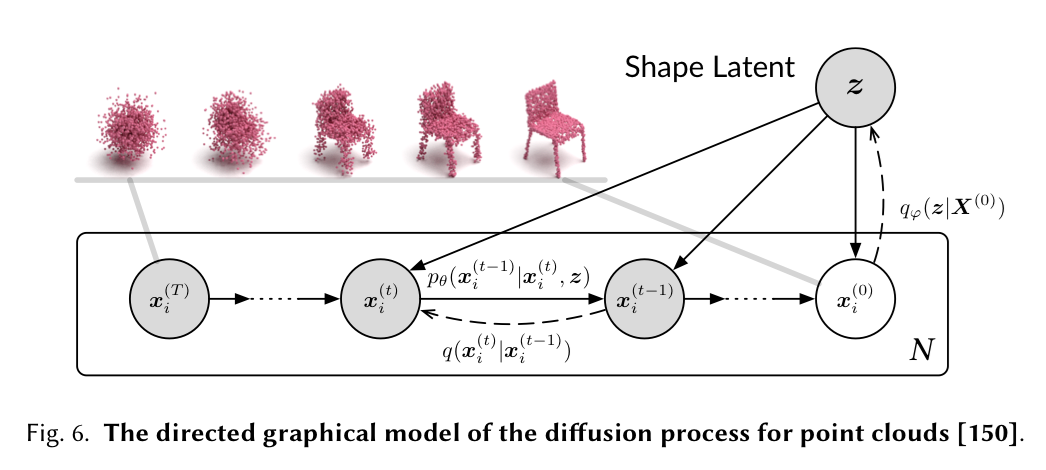
그림 6. 포인트 클라우드(point clouds)에 대한 확산 과정의 지향성 그래픽 모델 [150]

7.1.4 포인트 클라우드(Point Cloud) 완성과 생성

포인트 클라우드는 실제 세계의 객체를 포착하기 위한 3D 표현의 중요한 형태입니다. 그러나 스캔은 부분적인 관찰이나 자기 가림(self-occlusion)으로 인해 종종 불완전한 포인트 클라우드를 생성합니다. 최근 연구에서는 이러한 도전을 해결하기 위해 확산 모델(diffusion models)을 적용하여 누락된 부분을 추론하고 완전한 형태를 재구성하는 데 사용하고 있습니다. 이 작업은 3D 재구성, 증강 현실, 장면 이해(scene understanding)와 같은 다양한 하류 작업(downstream tasks)에 영향을 미칩니다 [151, 155, 274].

Luo et al. 2021 [150]은 포인트 클라우드를 열역학 시스템(thermodynamic system)에서의 입자로 취급하는 접근 방식을 취했으며, 원래 분포에서 잡음 분포(noise distribution)로의 확산을 촉진하기 위해 열 욕조(heat bath)를 사용했습니다. 한편, Point-Voxel Diffusion (PVD) 모델 [286]은 3D 형상의 포인트-복셀(point-voxel) 표현과 탈잡음 확산 모델(denoising diffusion models)을 결합합니다. Point Diffusion-Refinement (PDR) 모델 [155]은 조건부 DDPM(conditional DDPM)을 사용하여 부분 관찰로부터 거친 완성을 생성하며, 생성된 포인트 클라우드와 실제 데이터(ground truth) 간의 점별 매핑(point-wise mapping)을 설정합니다.

7.1.5 이상 탐지(Anomaly Detection)

이상 탐지는 기계 학습(machine learning) [209, 283]과 컴퓨터 비전(computer vision) [262]에서 중요하고 도전적인 문제입니다. 생성 모델(generative models)은 정상이나 건강한 참조 데이터를 모델링하는 데 있어 강력한 메커니즘을 가지고 있는 것으로 나타났습니다 [70, 87, 252]. AnoDDPM [252]은 입력 이미지를 손상시키고 이미지의 건강한 근사치를 재구성하기 위해 DDPM을 활용합니다. 이러한 접근 방식은 효과적인 샘플링과 안정적인 훈련 체계로 더 작은 데이터셋을 더 잘 모델링할 수 있기 때문에 적대적 훈련(adversarial training)을 기반으로 하는 대안보다 더 나은 성능을 발휘할 수 있습니다. DDPM-CD [70]는 DDPM을 통해 대규모의 비감독 원격 감지 이미지를 훈련 과정에 통합합니다. 사전 훈련된 DDPM을 활용하고 확산 모델 디코더(diffusion model decoder)에서의 다중 스케일 표현을 적용하여 원격 감지 이미지의 변화를 탐지합니다.

7.2 자연어 처리(Natural Language Processing)

자연어 처리는 텍스트나 오디오와 같은 다양한 출처에서 인간의 언어를 이해하고, 모델링하며, 관리하는 것을 목표로 합니다. 텍스트 생성은 자연어 처리에서 가장 중요하고 도전적인 과제 중 하나가 되었습니다[102, 138, 139]. 이는 주어진 입력 데이터(예: 시퀀스와 키워드)나 무작위 잡음을 바탕으로 인간 언어로 그럴듯하고 읽을 수 있는 텍스트를 작성하는 것을 목표로 합니다. 텍스트 생성을 위한 다양한 확산 모델 기반 접근법이 개발되었습니다. 이산 노이즈 제거 확산 확률 모델(Discrete Denoising Diffusion Probabilistic Models, D3PM) [6]은 문자 수준의 텍스트 생성을 위한 확산과 같은 생성 모델을 소개합니다[28]. 이는 균일한 전이 확률을 가진 손상 과정을 넘어서 다항 확산 모델[96]을 일반화합니다. 큰 자기회귀 언어 모델(Large autoregressive language models, LMs)은 고품질의 텍스트를 생성할 수 있습니다 $[18,35,185,279]$. 이 LMs를 실제 애플리케이션에 신뢰성 있게 배포하기 위해서는, 텍스트 생성 과정이 보통 제어 가능해야 합니다. 즉, 우리는 원하는 요구 사항(예: 주제, 구문 구조)을 만족하는 텍스트를 생성해야 한다는 의미입니다. 재학습 없이 언어 모델의 행동을 제어하는 것은 텍스트 생성에서 중요하고 큰 문제입니다[43, 117]. 비록 최근 방법들이 간단한 문장 속성(예: 감정)을 제어하는 데에 상당한 성공을 거두었지만[127, 263], 복잡하고 세밀한 제어(예: 구문 구조)에 대해서는 거의 진전이 없습니다. 더 복잡한 제어를 다루기 위해, 확산-LM(Diffusion-LM) [141]은 연속적인 확산을 기반으로 한 새로운 언어 모델을 제안합니다. 확산-LM은 가우시안 잡음 벡터의 시퀀스로 시작하여 점진적으로 단어에 해당하는 벡터로 노이즈를 제거합니다. 점진적인 노이즈 제거 단계는 계층적인 연속적인 잠재 표현을 생성하는 데 도움을 줍니다. 이 계층적이고 연속적인 잠재 변수는 간단한, 기울기 기반 방법으로 복잡한 제어를 달성할 수 있게 만들 수 있습니다. 아날로그 비트(Analog Bits) [32]는 이산 변수를 나타내기 위해 아날로그 비트를 생성하고, 자기 조건화(self-conditioning)와 비대칭 시간 간격으로 샘플 품질을 더욱 향상시킵니다. DiffuSeq [88]는 더 도전적인 텍스트 생성 과제를 수행하기 위한 새로운 조건부 확산 모델을 제안합니다.

7.3 시계열 데이터 모델링(Temporal Data Modeling)

7.3.1 시계열 보간(Time Series Imputation)

시계열 데이터는 많은 중요한 실제 응용 분야에서 널리 사용됩니다[60, 173, $265,280$]. 그럼에도 불구하고, 시계열은 기계적 또는 인위적 오류[213, 229, 269]로 인해 여러 가지 이유로 누락된 값들을 포함하고 있습니다. 최근 몇 년 동안, 결정론적 보간(deterministic imputation)[23, 27, 154]과 확률적 보간(probabilistic imputation)[65]을 포함하여 보간 방법들이 크게 발전했습니다. 조건부 점수 기반 확산 모델을 이용한 보간(Conditional Score-based Diffusion models for Imputation, CSDI)[230]은 점수 기반 확산 모델을 활용하는 새로운 시계열 보간 방법을 제시합니다. 특히, 시간 데이터 내의 상관관계를 활용하기 위해 자기 감독 학습(self-supervised training) 형태를 채택하여 확산 모델을 최적화합니다. 일부 실제 데이터셋에서의 적용은 이전 방법들보다 우수함을 드러냅니다. 제어된 확률적 미분 방정식(Controlled Stochastic Differential Equation, CSDE)[177]은 신경 제어 확률적 미분 방정식을 사용하여 확률적 역학을 모델링하는 새로운 확률적 프레임워크를 제안합니다. 구조화된 상태 공간 확산(Structured State Space Diffusion, SSSD)[1]은 조건부 확산 모델과 구조화된 상태 공간 모델[82]을 통합하여 특히 시계열의 장기 의존성을 포착합니다. 이는 시계열 보간과 예측 작업 모두에서 잘 수행됩니다.

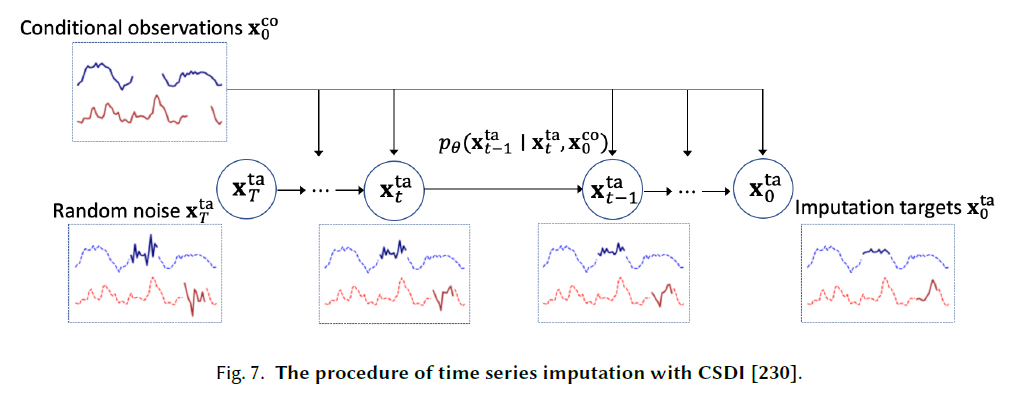
그림 7. CSDI[230]를 사용한 시계열 보간 절차.

7.3.2 시계열 예측(Time Series Forecasting)

시계열 예측은 일정 기간 동안 미래 값에 대한 예측 또는 예보를 하는 작업입니다. 신경 방법(neural methods)은 최근 단변량 점 예측 방법(univariate point forecasting methods)[172] 또는 단변량 확률적 방법(univariate probabilistic methods)[205]을 사용하여 예측 문제를 해결하기 위해 널리 사용되고 있습니다. 다변량 설정에서는 점 예측 방법(point forecasting methods)[140]과 가우시안 코퓰라(Gaussian copulas)[206], GANs[271], 정규화 흐름(normalizing flows)[192]을 사용하여 데이터 분포를 명시적으로 모델링하는 확률적 방법(probabilistic methods)도 있습니다. TimeGrad[191]는 다변량 확률적 시계열 예측을 위한 자기 회귀 모델(autoregressive model)을 제시하며, 각 시간 단계에서 데이터 분포의 그래디언트를 추정하여 샘플링합니다. 이는 점수 매칭(score matching)과 에너지 기반 방법(energy-based methods)과 밀접한 관련이 있는 확산 확률 모델(diffusion probabilistic models)을 활용합니다. 특히, 데이터 가능성에 대한 변분 경계(variational bound)를 최적화하여 그래디언트를 학습하고, 추론 시간에 Langevin 샘플링[220]을 사용하는 마르코프 체인(Markov chain)을 통해 백색 잡음(white noise)을 관심 있는 분포의 샘플로 변환합니다.

7.3.3 파형 신호 처리(Waveform Signal Processing)

전자, 음향학 및 관련 분야에서 신호의 파형은 시간에 대한 함수로서 그래프의 형태로 나타나며, 시간과 크기의 척도와는 독립적입니다. WaveGrad [29]는 데이터 밀도의 기울기를 추정하는 조건부 파형 생성 모델을 소개합니다. 이 모델은 가우시안 흰색 잡음 신호를 입력으로 받아 그래디언트 기반 샘플러를 사용하여 신호를 반복적으로 정제합니다. WaveGrad는 정제 단계의 수를 조정함으로써 추론 속도와 샘플 품질 사이의 자연스러운 교환을 가능하게 하며, 오디오 품질 측면에서 비자기회귀(nonautoregressive) 모델과 자기회귀(autoregressive) 모델 사이의 연결을 만듭니다. DiffWave [126]는 조건부 또는 무조건부 파형 생성을 위한 다재다능하고 효과적인 확률론적 확산 모델을 제시합니다. 이 모델은 비자기회귀(non-autoregressive)이며 데이터 가능성에 대한 변형된 변분 경계(variational bound)를 최적화함으로써 효율적으로 훈련됩니다. 또한, 클래스 조건부 생성(class-conditional generation) 및 무조건부 생성(unconditional generation)과 같은 다양한 파형 생성 작업에서 고품질 오디오를 생성합니다.

7.4 멀티 모달 학습(Multi-Modal Learning)

7.4.1 텍스트-이미지 생성(Text-to-Image Generation). 비전-언어 모델은 잠재적인 응용 프로그램의 수 [184]로 인해 최근 많은 관심을 받고 있습니다. 텍스트-이미지 생성은 서술적인 텍스트로부터 해당 이미지를 생성하는 작업입니다 [57, 116, 235]. 예시는 그림 8에 나와 있습니다. 혼합 확산(Blended diffusion) [7]은 사전 훈련된 DDPM [49]과 CLIP [184] 모델을 모두 활용하며, 자연어 안내를 사용하고 실제 및 다양한 이미지에 적용 가능한 일반 목적의 지역 기반 이미지 편집 솔루션을 제안합니다. 반면에, unCLIP (DALLE-2) [186]은 두 단계 접근 방식을 제안하는데, 텍스트 캡션에 따라 CLIP 기반 이미지 임베딩을 생성할 수 있는 사전 모델과 이미지 임베딩에 따라 이미지를 생성할 수 있는 확산 기반 디코더입니다. 최근에는 Imagen [201]이 텍스트-이미지 확산 모델과 성능 평가를 위한 종합적인 벤치마크를 제안합니다. Imagen은 VQ-GAN+CLIP [41], Latent Diffusion Models [146], DALL-E 2 [186]를 포함한 최신 접근 방식에 대해 잘 수행됨을 보여줍니다. 가이드 확산 모델 [49, 92]이 사실적인 샘플을 생성하는 능력과 텍스트-이미지 모델이 자유 형식의 프롬프트를 처리하는 능력에 영감을 받아, GLIDE [167]는 텍스트 조건부 이미지 합성 응용 프로그램에 가이드 확산을 적용합니다. VQ-Diffusion [83]은 텍스트-이미지 생성을 위한 벡터 양자화 확산 모델을 제안하며, 일방향 편향을 제거하고 누적 예측 오류를 피합니다.

7.4.2 텍스트-오디오 생성(Text-to-Audio Generation)

텍스트-오디오 생성은 일반 언어 텍스트를 음성 출력으로 변환하는 작업입니다 [136, 249]. Grad-TTS [180]는 점수 기반 디코더(score-based decoder)와 확산 모델(diffusion models)을 사용한 새로운 텍스트-음성 변환 모델을 제시합니다. 이 모델은 인코더에 의해 예측된 노이즈를 점진적으로 변환하며, 단조 정렬 탐색(Monotonic Alignment Search) [183] 방법으로 텍스트 입력과 더 잘 맞춥니다. Grad-TTS2 [119]는 Grad-TTS를 적응적으로 개선합니다. Diffsound [261]는 이산 확산 모델(discrete diffusion model) [6, 215]을 기반으로 한 비자동 회귀 디코더(non-autoregressive decoder)를 제시하며, 이는 모든 멜-스펙트로그램 토큰(mel-spectrogram tokens)을 단일 단계에서 예측하고, 다음 단계에서 예측된 토큰을 정제합니다. EdiTTS [228]는 점수 기반 텍스트-음성 변환 모델을 활용하여 대략적으로 수정된 멜-스펙트로그램 사전(mel-spectrogram prior)을 정제합니다. 데이터 밀도의 기울기를 추정하는 대신, ProDiff [99]는 깨끗한 데이터를 직접 예측함으로써 노이즈 제거 확산 모델(denoising diffusion model)을 파라미터화합니다. ACM에 제출된 원고

그림 8. GLIDE [167]에 의해 생성된 텍스트-이미지 결과.

7.5 견고한 학습(Robust Learning)

강인한 학습(robust learning)은 적대적인 변형(adversarial perturbations)이나 노이즈에 강한 학습 네트워크를 돕는 방어 방법들의 한 분류입니다 [16, 168, 179, 240, 248, 270]. 적대적 훈련(adversarial training) [157]이 이미지 분류기에 대한 적대적 공격에 대한 표준 방어 방법으로 여겨지는 반면, 적대적 정화(adversarial purification)는 독립적인 정화 모델을 사용하여 공격받은 이미지를 깨끗한 이미지로 정화하는 대안적인 방어 방법으로 중요한 성능을 보여주었습니다 [270]. 적대적 예제가 주어지면, DiffPure [168]는 전방 확산 과정(forward diffusion process)을 따라 소량의 노이즈로 그것을 확산시킨 후 역 생성 과정(reverse generative process)으로 깨끗한 이미지를 복원합니다. 적응형 노이즈 제거 정화(Adaptive Denoising Purification, ADP) [270]는 노이즈 제거 점수 매칭(denoising score matching) [238]으로 훈련된 EBM이 단 몇 단계 내에 공격받은 이미지를 효과적으로 정화할 수 있음을 보여줍니다. 또한, 정화 전에 이미지에 무작위 노이즈를 주입하는 효과적인 무작위 정화 방식을 제안합니다. 투영된 그래디언트 하강(Projected Gradient Descent, PGD) [16]은 모델에 구애받지 않는 적대적 방어를 목표로 하고 고품질의 노이즈 제거 결과를 제공하는 새로운 확산 기반 전처리 강화 방법을 제시합니다. 또한, 일부 연구에서는 고급 적대적 정화를 위해 안내 확산 과정을 적용하는 것을 제안합니다 [240, 248].

7.6 학제 간 응용

7.6.1 분자 그래프 모델링. 그래프 신경망(Graph Neural Networks, GNN) [85, 251, 266, 285]과 해당 표현 학습(representation learning) 기술들은 속성 예측 $[59,71]$부터 분자 생성 $[105,111,152,211]$에 이르는 다양한 작업에서 분자 그래프를 모델링하는 것을 포함하여 많은 분야에서 큰 성공을 거두었습니다. 여기서 분자는 자연스럽게 노드-엣지 그래프로 표현됩니다. 다양한 응용 분야에서의 효과에도 불구하고, 더 본질적이고 정보적인 속성들이 분자 그래프 모델링을 강화하기 위해 확산 모델과 결합하기 시작했습니다. 비틀림 확산(torsional diffusion) [107]은 비틀림 각도의 공간에서 작업을 수행하는 새로운 확산 프레임워크를 제시하며, 고차원 공간에서의 확산 과정과 외재적-내재적 평가 모델을 사용합니다. GeoDiff [259]는 동등한 마르코프 커널(equivariant Markov kernels)로 진화하는 마르코프 체인이 불변 분포(invariant distribution)를 생성할 수 있음을 보여주고, 바람직한 동등성 속성을 보존하기 위한 마르코프 커널의 블록을 설계합니다. 또한, 동등성 속성을 3D 분자 생성 [94]과 단백질 생성 [3, 13]에 통합하는 다른 연구들도 있습니다. 분자 역학을 시뮬레이션하기 위한 고전적인 힘장 방법에 의해 동기를 얻은 ConfGF [210]는 분자 구조 생성에서 원자 좌표의 로그 밀도의 그래디언트 필드를 직접 추정합니다.

7.6.2 재료 설계. 고체 상태 재료는 수많은 핵심 기술의 중요한 기반입니다 [19]. 결정 확산 변분 오토인코더(Crystal Diffusion Variational Autoencoder, CDVAE) [256]는 안정성을 유도적 편향(inductive bias)으로 통합하여 노이즈

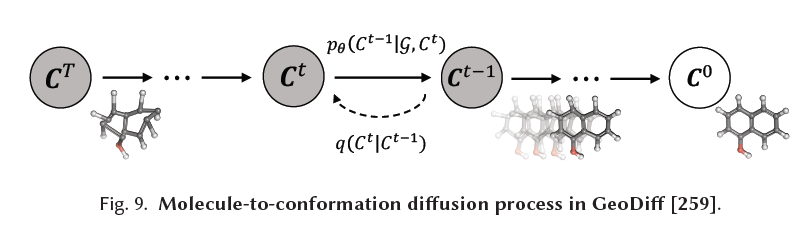
그림 9. GeoDiff [259]에서 분자에서 구조체로의 확산 과정.

조건부 점수 네트워크(conditional score network)는 순열(permutation), 이동(translation), 회전(rotation), 그리고 주기적 불변성(periodic invariance)의 특성을 동시에 활용합니다. Luo et al. (2022) [153]은 동등한 확산(equivariant diffusion)을 사용하여 보완 결정 영역(complementarity-determining regions)의 시퀀스와 구조를 모델링하고, 특정 항원 구조를 목표로 하여 원자 해상도에서 항체를 생성합니다.

7.6.3 의료 영상 복원(Medical Image Reconstruction). 역문제(inverse problem)는 관찰된 측정값으로부터 알려지지 않은 신호를 복구하는 것이며, 이는 컴퓨터 단층 촬영(Computed Tomography, CT)과 자기 공명 영상(Magnetic Resonance Imaging, MRI) [36, 37, 178, 224, 257]의 의료 영상 복원에서 중요한 문제입니다. Song et al. (2021) [224]은 점수 기반 생성 모델(score-based generative model)을 활용하여 사전 지식과 관찰된 측정값 모두와 일치하는 이미지를 재구성합니다. Chung et al. (2022) [38]은 노이즈 제거 점수 매칭(denoising score matching)으로 연속 시간 의존 점수 함수(continuous time-dependent score function)를 훈련하고, 평가 단계에서 수치적 SDE 해결기(numerical SDE solver)와 데이터 일관성 단계(data consistency step) 사이를 반복하여 복원합니다. Peng et al. (2022) [178]은 관찰된 k-공간 신호를 주어진 역확산 과정(reverse-diffusion process)을 점진적으로 안내하여 MR 복원을 수행하고, 효율적인 샘플링을 위한 조밀한 샘플링 알고리즘(coarse-to-fine sampling algorithm)을 제안합니다.

8 미래 방향(FUTURE DIRECTIONS)

확산 모델에 대한 연구는 초기 단계에 있으며, 이론적 및 경험적 측면에서 큰 개선 가능성을 가지고 있습니다. 앞서 언급한 바와 같이, 주요 연구 방향은 효율적인 샘플링과 개선된 가능성(likelihood)을 포함하며, 확산 모델이 특별한 데이터 구조를 다루고, 다른 유형의 생성 모델과 인터페이스하며, 다양한 응용 분야에 맞게 조정될 수 있는 방법을 탐색하는 것입니다. 또한, 우리는 확산 모델에 대한 미래 연구가 다음과 같은 분야로 확장될 것으로 예상합니다.

가정 재검토(Revisiting Assumptions). 확산 모델에서의 많은 전형적인 가정들은 재검토되고 분석되어야 합니다. 예를 들어, 확산 모델의 전방 과정(forward process)이 데이터의 모든 정보를 완전히 지우고 사전 분포(prior distribution)와 동등하게 만든다는 가정은 항상 유지되지 않을 수 있습니다. 실제로, 유한한 시간 내에 정보를 완전히 제거하는 것은 불가능합니다. 전방 노이징 과정(forward noising process)을 언제 중단해야 샘플링 효율성과 샘플 품질 사이의 균형을 맞출 수 있는지 이해하는 것은 매우 흥미로운 주제입니다 [66]. 최근 슈뢰딩거 브릿지(Schrödinger bridges)와 최적 운송(optimal transport) [31, 44, 46, 212, 218]에 대한 진전은 유한한 시간 내에 특정 사전 분포로 수렴할 수 있는 확산 모델의 새로운 공식을 제안하는 유망한 대안적 해결책을 제시합니다.

이론적 이해. 확산 모델(diffusion models)은 특히 적대적 학습(adversarial training)에 의존하지 않고도 대부분의 응용 분야에서 생성적 적대 신경망(GANs)에 필적할 수 있는 강력한 프레임워크로 부상했습니다. 이 잠재력을 활용하는 데 있어 중요한 것은 확산 모델이 특정 작업에 대해 대안들보다 효과적인 이유와 시기를 이해하는 것입니다. 변분 오토인코더(variational autoencoders), 에너지 기반 모델(energy-based models), 자기회귀 모델(autoregressive models)과 같은 다른 유형의 생성 모델과 확산 모델을 구별하는 근본적인 특성을 식별하는 것이 중요합니다. 이러한 차이점을 이해하는 것은 확산 모델이 우수한 품질의 샘플을 생성하면서 최고의 가능성(likelihood)을 달성할 수 있는 이유를 명확히 할 것입니다. 또한 확산 모델의 다양한 하이퍼파라미터를 체계적으로 선택하고 결정하기 위한 이론적 지침을 개발할 필요성도 마찬가지로 중요합니다.

ACM에 제출된 원고

잠재 표현. 변분 오토인코더나 생성적 적대 신경망과 달리, 확산 모델은 데이터의 잠재 공간에서 좋은 표현을 제공하는 데 덜 효과적입니다. 그 결과, 의미론적 표현에 기반한 데이터 조작과 같은 작업에 쉽게 사용될 수 없습니다. 또한, 확산 모델에서의 잠재 공간은 종종 데이터 공간과 동일한 차원을 가지기 때문에 샘플링 효율성이 부정적으로 영향을 받고 모델이 표현 체계를 잘 학습하지 못할 수 있습니다 [106].

9 결론

우리는 다양한 관점에서 확산 모델에 대한 포괄적인 검토를 제공했습니다. 우리는 DDPMs, SGMs, Score SDEs의 세 가지 기본적인 공식에 대한 자체 포함적인 소개로 시작했습니다. 그런 다음 확산 모델을 개선하기 위한 최근 노력을 논의하며, 샘플링 효율성, 가능성 최대화, 특수 구조를 가진 데이터를 위한 새로운 기술의 세 가지 주요 방향을 강조했습니다. 우리는 또한 확산 모델과 다른 생성 모델 간의 연결을 탐구하고 두 모델을 결합할 때의 잠재적 이점을 개요했습니다. 여섯 개 분야에 걸친 응용 분야 조사는 확산 모델의 광범위한 잠재력을 보여주었습니다. 마지막으로, 우리는 미래 연구를 위한 가능한 방향을 개요했습니다.