[논문리뷰] Diffusion Models Beat GANs on Image Synthesis (ADM, 2021)

0. Abstract

• Diffusion Models이 이전까지 SOTA였던 GAN보다 우수함을 실험적으로 보여줌
• 처음으로 diffusion guidance를 제시함
• 깃헙 guided-diffusion 레포

1. Introduction

• GAN
  • image generation tasks에서 SOTA
    • FID, Inception Score, Precision
  • limitations
    • diversity가 떨어짐
    • 학습이 불안정함
    • 위의 단점들 때문에 확장성이 떨어짐
• GAN vs. Diffusion
  • 아직까지는 GAN이 성능이 더 좋음
    1) GAN은 오랜 시간 연구되면서 충분히 튜닝되었기 때문. 반면 디퓨젼은 갓 태어난 날것이니까
    2) GAN은 diversity <-> fidelity tradeoff에서 fidelity를 선택했기 때문에 퀄리티가 좋은 것
• 본 논문에서는 diffusion을 약간 손보면 GAN보다 성능이 좋아짐을 실험적으로 보임

2. Background

1. Diffusion Models
2. Improved DDPM
   • Contributions
     • variance $\Sigma_{\theta}(x_{t},t)$를 상수로 fix하는 것은 optimal이 아니라고 주장
       • 기존 DDPM에서는 $\Sigma_{\theta}(\mathrm{x}_{t},t)=\beta_{t} I$로 세팅했었다
     • propose to parameterize $\Sigma_{\theta}(x_{t},t)=\mathrm{exp}(v\ \mathrm{log}\ \beta_{t}\ +\ (1-v)\ \mathrm{log}\ \tilde{\beta}_{t})$
       • recap DDPM
         • reverse process $p_{\theta}(\mathrm{x}_{t-1}|\mathrm{x}_{t})$를 학습하려면 forward process $q(\mathrm{x}_{t}|\mathrm{x}_{t-1})$를 뒤집은 forward posterior $q(\mathrm{x}_{t-1}|\mathrm{x}_{t})$와 비교해야 했다
         • 그런데 $q(\mathrm{x}_{t-1}|\mathrm{x}_{t})$는 구하기 어려우므로 계산이 쉬운 $q(\mathrm{x}_{t-1}|\mathrm{x}_{t},\mathrm{x}_{0})$를 대신 썼음
         • forward process $q(\mathrm{x}_{t}|\mathrm{x}_{t-1}):=\mathcal{N}(\mathrm{x}_{t};\sqrt{1-\beta}\mathrm{x}_{t-1},\beta_{t}I)$로 주어졌고
         • forward posterior는
           • $q(\mathrm{x}_{t-1}|\mathrm{x}_{t},\mathrm{x}_{0})=\mathcal{N}(\mathrm{x}_{t-1};\tilde{\mu}(\mathrm{x}_{t},\mathrm{x}_{0}),\tilde{\beta}_{t}I)$
           • $\mathrm{where}\ \ \ \tilde{\mu}_{t}(\mathrm{x}_{t},\mathrm{x}_{0}):=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_{t}}{1-\bar{\alpha}_{t}}\mathrm{x}_{0}+\frac{\sqrt{\alpha_{t}}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}\mathrm{x}_{t}\ \ \ \mathrm{and}\ \ \ \tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$
           • 로 주어짐
       • 따라서 $\beta_{t}, \tilde{\beta}_{t}$는 각각 reverse process variance의 upper&lower bound에 해당함
     • $\epsilon$과 $\Sigma$를 동시에 학습하기 위해 weighted sum objective $L_{\mathrm{simple}}+\lambda L_{\mathrm{vlb}}$를 도입함
   • sample quality를 떨어뜨리지 않고도 sampling step 수를 줄일 수 있음
3. DDIM
   • 본 논문에서는 Improved DDPM의 objective & parameterization, DDIM의 sampling strategy를 차용함
   • quality metrics로는 FID를 메인으로 사용하였음

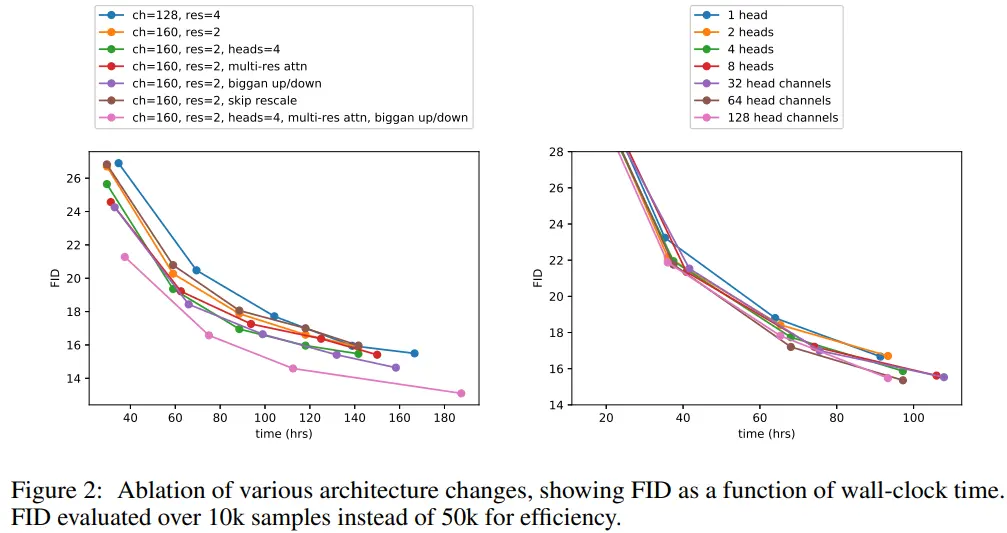
3. Architecture Improvements

• previous works

  • DDPM introduced the UNet architecture
  • score-SDE (NCSN++, DDPM++) found that further changes to the UNet architecture improved performance on the CIFAR-10 & CelebA-64

• architectural changes

  • Increasing depth vs. width, holding model size relatively constant
  • Increasing the number of attention heads
  • Using attention at 32x32, 16x16, and 8x8 resolutions rather than only at 16x16
  • Using the BigGAN residual block for upsampling & downsampling the activations (from score-SDE)
  • Rescaling residual connections with $\frac{1}{\sqrt{2}}$ (from [score-SDE], StyleGAN)

• ImageNet 128x128으로 학습시키고 FID로 성능 평가함

  • 

• Adaptive Group Normalization

  • AdaGN이라는 layer로도 실험해 봄
    • groupnorm 연산 이후 residual block과 더불어 timestep and class embedding도 함께 활용하기
    • adaptive instance norm(AdaIN), FiLM과 유사함
    • $\mathrm{AdaGN}(h,y)=y_{s}\ \mathrm{GroupNorm}(h)+y_{b}$
      • $h$: intermediate activations of the residual block
      • $y=[y_{s},y_{b}]$: obtained from a linear projection of the timestep & class embedding

• Setting default model architectures

  • 2 residual blocks per resolution
  • multiple heads with 64 channels per head
  • attention at 32, 16 and 8 resolutions
  • BigGAN residual blocks for up and downsampling
  • AdaGN for injecting timestep & class embeddings into residual blocks

4. Classifier Guidance

4.0. How to condition diffusion models?

• 우리는 이미 AdaGN layer에서 class information을 주입하고 있음
• classifier $p(y|x)$를 이용해서 diffusion generation을 발전시킬 수 있음
  • previous works(DPM, score-SDE)에 의하면 pre-trained diffusion model을 classifier gradient를 이용해서 컨디셔닝 할 수 있다
  • noisy image $x_{t}$를 보고 label을 판단하는 classifier $p_{\phi}(y|x_{t},t)$를 훈련시키고
  • gradient $\nabla_{x_{t}}\ \mathrm{log}\ p_{\phi}(y|x_{t},t)$를 diffusion sampling process 때 반영하면 label $y$에 대한 컨디셔닝이 된다
• 편의를 위해 notation에서 일부 $t$는 생략하였음 ($p_{\phi}(y|x_{t},t)=p_{\phi}(y|x_{t}), \epsilon_{\theta}(x_{t},t)=\epsilon_{\theta}(x_{t}$)

4.1. Conditional Reverse Noising Process

• unconditional reverse process $p_{\theta}(x_{t}|x_{t+1})$를 label $y$로 컨디셔닝한 확률은 아래와 같이 나타낼 수 있다.

  • $p_{\theta,\phi}(x_{t}|x_{t+1},y)=Z\ p_{\theta}(x_{t}|x_{t+1})\ p_{\phi}(y|x_{t})$
  • $Z$: 확률의 합을 1로 만들어주는 normalizing constant
  • 본래 이 식은 intractable하지만 DPM에 의해 perturb Gaussian distribution으로 근사될 수 있다
• $\begin{aligned} p_{\theta}(x_{t}|x_{t+1}) &= \mathcal{N}(\mu,\Sigma)\\ \mathrm{log}\ p_{\theta}(x_{t}|x_{t+1}) &= - \frac{1}{2}(x_{t}-\mu)^{T}\Sigma^{-1}(x_{t}-\mu)+C \end{aligned}$

• $\mathrm{log}\ p_{\phi}(y|x_{t})$는 $\Sigma^{-1}$보다 낮은 curvature를 가진다 (???)

  • diffusion step 수가 많아질 수록 $||\Sigma|| \rightarrow 0$으로 가기 때문
  • 따라서 $\mathrm{log}\ p_{\phi}(y|x_{t})$를 $x_{t}=\mu$ 근처에서의 Taylor expansion으로 근사할 수 있다

  $\begin{aligned} \mathrm{log}\ p_{\phi}(y|x_{t}) &\approx \mathrm{log}\ p_{\phi}(y|x_{t})|_{x_{t}=\mu} + (x_{t}-\mu)\ \nabla_{x_{t}}\ \mathrm{log}\ p_{\phi}(y|x_{t})|_{x_{t}=\mu}\\ &= (x_{t}-\mu)g + C_{1} \end{aligned}$

  • 여기서 $g= \nabla_{x_{t}}\ \mathrm{log}\ p_{\phi}(y|x_{t})|_{x_{t}=\mu}$이고 $C_{1}$은 constant이므로

• conditional transition operator는 unconditional operator와 비슷한 Gaussian으로 근사되지만, mean이 $\Sigma g$만큼 shift된다

  • 

  • diffusion model output $\mu, \Sigma$와 classifier gradient를 구한 후, $\mu$에 classifier gradient를 더해준다

  • $s$는 scale factor

4.2. Conditional Sampling for DDIM

• 4.1.의 알고리즘은 stochastic diffusion sampling에만 적용 가능하고, DDIM 같은 deterministic sampling에는 쓸 수 없다
• score-based conditioning trick 이용하기
  • connection between diffusion models and score matching: $\nabla_{x_{t}}\ \mathrm{log}\ p_{\theta}(x_{t})=- \frac{1}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(x_{t})$
• 이제 $p(x_{t})p(y|x_{t})$를 score function을 포함하는 꼴로 변형한 뒤 거기에 diffusion network $\epsilon_{\theta}$를 대입해보자

• 이제 새로운 epsilon prediction $\hat{\epsilon}(x_{t})$를 아래와 같이 정의한다
  • 이게 어떻게 나온건지?? 이해 안 됨
    $\hat{\epsilon}(x_{t})=\epsilon_{\theta}(x_{t})-\sqrt{1-\bar{\alpha}_{t}}\ \nabla_{x_{t}}\ \mathrm{log}\ p_{\phi}(y|x_{t})$
  • DDIM같은 샘플러를 이용할 때 기존의 $\epsilon$ 대신 $\hat{\epsilon}$을 쓰면 된다
  • 

4.3. Scaling Classifier Gradients

• Training classifier

  • UNet의 downsampling trunk에 attention pool을 붙여서 classifier를 만들었다
  • diffusion model 학습할 때 들어가는 input을 classifier에도 input으로 넣어서 학습함
  • 학습된 classifier를 classifier guidance에 이용

• gradient scale $s$

  • Figure 4 참고
  • $s=1$로 놓으면 원하는 클래스의 결과가 잘 안 나왔다
  • $s=10$ 정도로 높이면 거의 100% 해당 클래스로 분류되는 결과가 나왔다
  • $s$의 값이 커질수록 classifier gradient의 반영 비율이 exponential하게 높아지기 때문
  • 

• with conditional diffusion model

  • Table 4 참고
  • 여태까지는 unconditional model $p(x)$에 대한 classifier guidance만 다뤘음
  • conditional diffusion model $p(x|y)$에도 똑같은 방식으로 guidance를 줄 수 있다
  • unconditional/conditional model 모두 guidance를 줬을 때 결과물이 좋았고, conditional model + guidance 둘 다 썼을 때 가장 좋은 FID를 달성할 수 있었다

• GAN과의 비교

  • Figure 5 참고
  • BigGAN-deep과 비교했을 때, classifier guidance가 FID<->IS tradeoff 면에서는 우수하지만 precision<->recall tradeoff 면에서는 GAN보다 약간 뒤쳐졌다