[ML] Logistic regression (로지스틱 회귀)

Logistic regression (로지스틱 회귀)

• binary classification (이진 분류) 를 위한 선형 모델
  • 이름은 regression 이지만 regression (회귀) 이 아닌 classification (분류) 모델

• odds ratio (오즈비, 승산비) : 특정 이벤트가 발생할 확률
  • ex) $P \over 1-P$

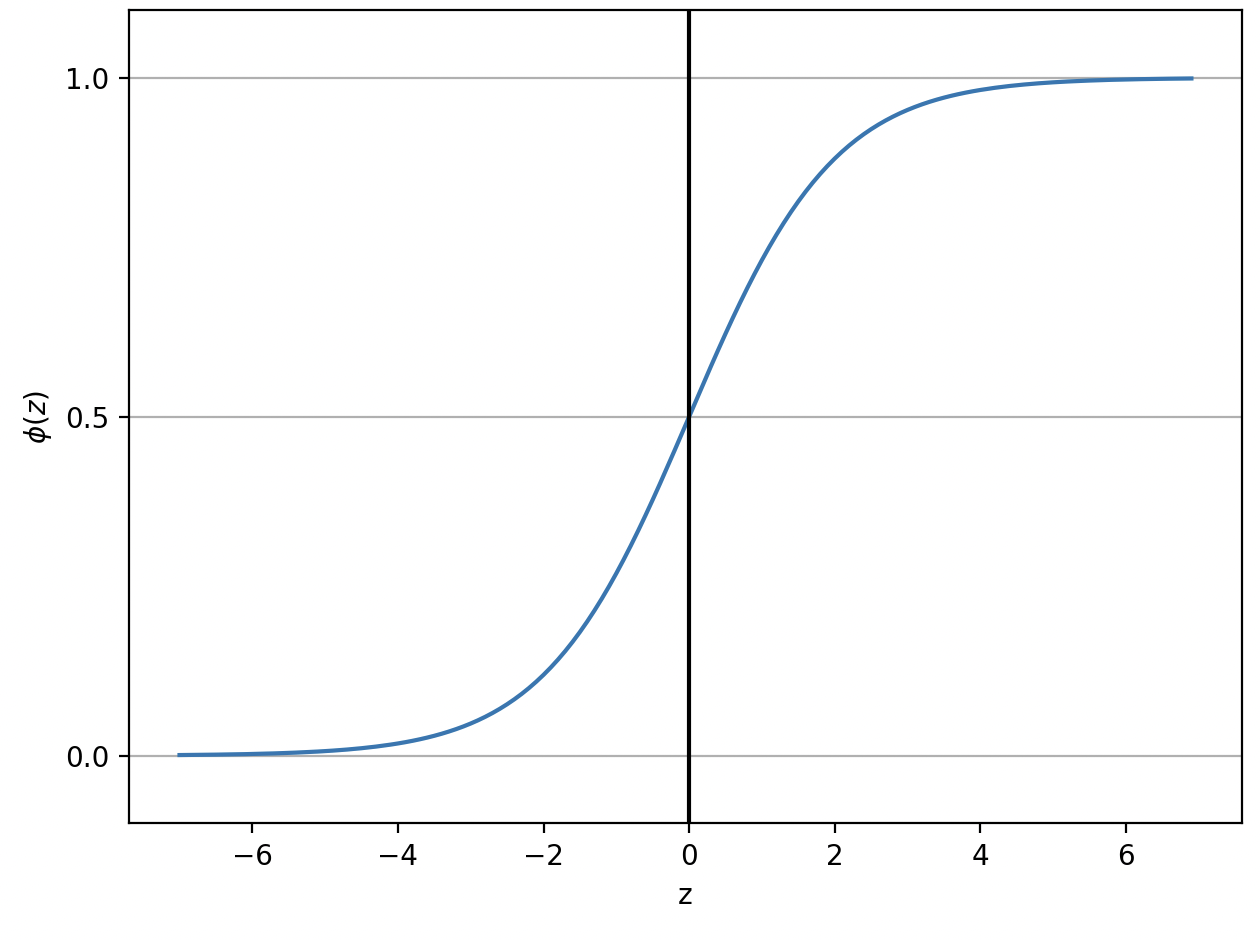
logistic sigmoid funciton (= sigmoid function)

• $\phi(z)= \frac{1}{1 + e^-z}$
• 로지스틱 시그모이드 함수, 시그모이드 함수
  • 로지스틱 회귀에서 activation function(활성화 홤수) 로 사용
  • s자 형태를 그리는 함수
  • z 값에 따라 0, 1에 수렴. 중간값 $\phi(0) = 0.5$

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

def show_sigmoid():
    """
    -7 ~ 7 범위의 sigmoid 시각화
    :return:
    """
    z = np.arange(-7, 7, 0.1)
    phi_z = sigmoid(z)
    plt.plot(z, phi_z)
    plt.axvline(0.0, color='k')
    plt.ylim(-0.1, 1.1)

    plt.xlabel('z')
    plt.ylabel('$\phi (z)$')
    # y축 눈금선
    plt.yticks([0.0, 0.5, 1.0])

    ax = plt.gca()
    ax.yaxis.grid(True)
    plt.tight_layout()
    plt.show()

if __name__=="__main__":
    show_sigmoid()

Scikit-learn 으로 logistic regression training

• 의존성 패키지 설치

 pipenv install scikit-learn numpy
 pipenv install matplotlib

• iris 데이터셋으로 분류 및 시각화

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt

import numpy as np


def train_logistic_regression():
    """
    iris(붓꽃) 데이터셋으로 꽃받침 길이, 꽃잎 길이 2개 feature 로 분류하기
    :return:
    """
    iris_dataset = datasets.load_iris()
    x = iris_dataset.data[:, [2, 3]]  # 꽃 데이터셋 중 일부 feature 만 추출 (꽃받침, 꽃길이)
    y = iris_dataset.target  # 꽃 품종 label

    # test_size : test data와 training data 비율. 0.3이면 test 30%, training 70%
    # random_state: 데이터셋을 섞기 위해 사용되는 random seed. 고정일 경우 매번 동일하게 재현
    # stratify : stratification (계층화). training, test 데이터 셋의 label 비율을 input 데이터셋과 동일하게 함
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=1, stratify=y)

    print(f'class label : {np.unique(y)}')

    # stratification 결과 체크
    print(f'y original data set label count : {np.bincount(y)}')
    print(f'y training data set label count : {np.bincount(y_train)}')
    print(f'y test data set label count : {np.bincount(y_test)}')

    # feature 표준화
    sc = StandardScaler()
    # traing data set 의 feature dimension 마다 평균과 표준 편차 계산
    sc.fit(x_train)

    # transform: 평균과 표준 편차로 data set 을 표준화
    x_train_std = sc.transform(x_train)
    x_test_std = sc.transform(x_test)

    # logistic regression
    lr = LogisticRegression(C=100.0, random_state=1)
    lr.fit(x_train_std, y_train)

    print(f'predict_proba (class 소속 확률) :\n {lr.predict_proba(x_test_std[:3, :])}')
    print(f'predict (class label) :\n {lr.predict(x_test_std[:3, :])}')
    
    # 시각화를 위해 training, test data set 결합
    x_combined_std = np.vstack((x_train_std, x_test_std))
    y_combined = np.hstack((y_train, y_test))

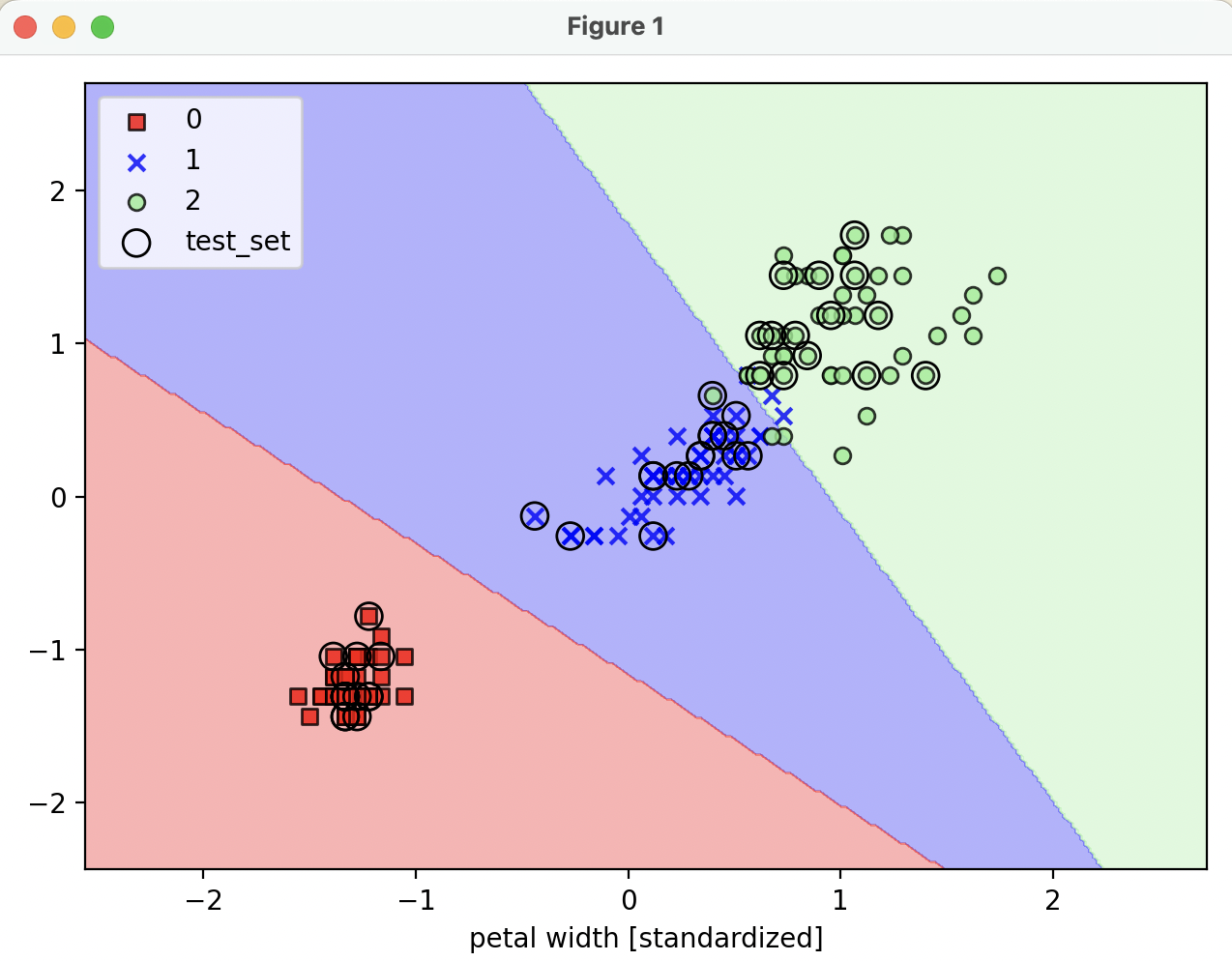
    plot_decision_regions(x=x_combined_std, y=y_combined, classifier=lr, test_idx=range(105, 150))
    plt.xlabel('petal length [standardized]')
    plt.xlabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()

• 시각화 함수 정의

def plot_decision_regions(x, y, classifier, test_idx=None, resolution=0.02):
    """
    시각화
    :param x: 붓꽃 데이터셋 feature (0번 열 : 꽃받침 길이, 1번 열 : 꽃잎 길이)
    :param y: class label
    :param classifier: 분류기
    :param test_idx:
    :param resolution:
    :return:
    """
    # 마커, 컬러맵 설정
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # decision boundary (결정 경계) 그리기
    # feature
    x1_min, x1_max = x[:, 0].min() - 1, x[:, 0].max() + 1  # feature column 0 -> 꽃받침 길이
    x2_min, x2_max = x[:, 1].min() - 1, x[:, 1].max() + 1  # feature column 1 ->  꽃잎 길이

    # meshgrid : 축에 해당하는 1차원 배열을 받아 벡터 공간의 모든 좌표를 담은 행렬을 반환
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    # ravel : 배열을 1차원 배열로 펼치기
    # T : transpose
    # 2개 배열을 펼치고 각 행으로 붙이고 transpose 하여 2개의 열로 변환, 이후 class label 예측
    z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    # xx1, xx2 와 같은 차원의 그리드로 크기 변경
    z = z.reshape(xx1.shape)
    # contourf : 등고선 그래프 그리기
    plt.contourf(xx1, xx2, z, alpha=0.3, cmap=cmap)
    # x, y축 limit 설정
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=x[y == cl, 0], y=x[y == cl, 1],
                    alpha=0.8, c=colors[idx],
                    marker=markers[idx], label=cl,
                    edgecolor='black')

    if test_idx:
        x_test, y_test = x[test_idx, :], y[test_idx]

    plt.scatter(x_test[:, 0], x_test[:, 1],
                facecolors='none', edgecolor='black', alpha=1.0,
                linewidth=1, marker='o',
                s=100, label='test_set')

• 시각화 결과

• predict_proba : 각 class 에 소속할 확률
  • -> 가장 큰 값의 column 이 예측 class label 이 됨
  • 직접 사용하기보단 pridict 메소드로 class label 을 가져오는 편

print(f'predict_proba (class 소속 확률) :\n {lr.predict_proba(x_test_std[:3, :])}')
print(f'predict (class label) :\n {lr.predict(x_test_std[:3, :])}')

# 실행 결과
predict_proba (class 소속 확률) :
 [[1.52213484e-12 3.85303417e-04 9.99614697e-01]
 [9.93560717e-01 6.43928295e-03 1.14112016e-15]
 [9.98655228e-01 1.34477208e-03 1.76178271e-17]]
predict (class label) :
 [2 0 0]

reference

• 서적 '머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 개정 3판'