[ML] TDD와 BDD 개요, 확률적 속성 문제, ML 성능 평가 지표

TDD Test-Driven Development

• TDD 의 규칙
  • 코드 작성 전 자동화된 실패 테스트(failing automated test)를 먼저 만들기
  • 중복 제거
• TDD 에서 지켜야할 사항
  • 프로그램 동작 behavior 이 의도한대로 바뀌었는지 추적하는 코드 작성
  • 각 iteration 단계 후 제대로 작동하고 빠른 반복수행 사이클
  • 버그에 대한 명확한 정의

TDD 사이클

• Red, Green, Refactor 3 단계

• Red

  • 실패 테스트 (failing test) 를 먼저 작성
  • ML 에서의 baseline test : 기준치가 될 최소한의 모델 성능 기준
    • 완전 랜덤, 항상 같은 결과 등등

• Green

  • 테스트 코드를 성공시키기 위한 최소한의 코드 작성
  • 기능 구현보다 테스트를 통과하는 것이 기준

• Refactor

  • 코드를 리팩토링하여 품질과 유지보수성을 높인다.

BDD Behavior-driven development

• TDD 에 비즈니스 고려사항을 추가한 것 BDD 소개
  • 작성된 테스트가 비즈니스 이해 관계자에게 설명할만한 가치가 있는가?

• Given-When-Then (GWT) 패턴

  • 주어진 조건 Given, 언제 When, 그러고 나면 Then 3단계로 구성
  • ex) 빈 데이터세트가 주어지고(Given), 분류분석기 학습이 완료된 상태면(When), 유효하지 않은 명령으로 exception 처리 (Then)
  • TDD 에서 꼭 지켜야할 사항은 아니다

• Given

  • 테스트 내용을 작성
  • ex) 데이터를 읽거나, 데이터의 특정 상황을 이슈화, 특정 사항을 처리하는 것에 대한 테스트

• When

  • 테스트하려는 동작을 시작하게 하는 action
  • ex) 추론을 시행

• Then

  • 변수, return 값 등의 상태 확인
  • ex)

테스트 예제

• nose 를 이용한 테스트

  • 의존성 설치
    pip3 install nose

• Red 단계 테스트 코드 작성

  • NumberGuesser 클래스를 정의하지 않았기 때문에 에러 발생
  • -> 에러를 해결하면 Green 단계로 넘어감

def given_no_information_when_asked_to_guess_test():
  # given (주어진 조건)
  number_guesser = NumberGuesser()
  # when (언제)
  guessed_number = number_guesser.guess()
  # then (그러고 나면)
  assert guessed_number is None, 'there should be no guess.'

# 실행결과
jungahn@userui-MacBookPro-66 Chapter 1 % nosetests
E
======================================================================
ERROR: number_guesser_tests.given_no_information_when_asked_to_guess_test
----------------------------------------------------------------------
Traceback (most recent call last):
  File "/Users/jungahn/.pyenv/versions/3.8.17/lib/python3.8/site-packages/nose/case.py", line 198, in runTest
    self.test(*self.arg)
  File "/Users/jungahn/Desktop/workspace/test-driven-machine-learning/TestDrivenMachineLearning/Chapter 1/number_guesser_tests.py", line 5, in given_no_information_when_asked_to_guess_test
    number_guesser = NumberGuesser()
NameError: name 'NumberGuesser' is not defined

• Green 단계
  • 기능은 없지만 NumberGuesser 클래스와 guess 메소드 정의, import 구문 추가로 테스트는 성공

# 아무 기능 없지만 최소한 테스트 실패는 하지 않는 코드
class NumberGuesser:
  def guess(self):
    return None

from NumberGuesser import NumberGuesser

def given_no_information_when_asked_to_guess_test():
  # given
  number_guesser = NumberGuesser()
  # when
  guessed_number = number_guesser.guess()
  # then
  assert guessed_number is None, 'there should be no guess.'

# 실행 결과 -> 테스트 성공은 한다.
jungahn@userui-MacBookPro-66 Chapter 1 % nosetests
.
----------------------------------------------------------------------
Ran 1 test in 0.001s

OK

확률적 속성 (Randomness) 문제 해결

import random

class NumberGuesser:
    """앞선 입력을 기억하고, 그중 랜덤하게 응답하도록 수정"""

    def __init__(self):
        self._guessed_numbers = []

    def numbers_were(self, guessed_numbers):
        self._guessed_numbers += guessed_numbers

    def number_was(self, guessed_number):
        self._guessed_numbers.append(guessed_number)

    def guess(self):
        if self._guessed_numbers == []:
            return None
        return random.choice(self._guessed_numbers)

• [1,2,5] 입력을 기억시키고, 100회 예측을 수행
  • -> 예측 결과들은 기억된 배열 [1,2,5] 중에서 있어야한다.

def given_multiple_datapoints_when_asked_to_guess_many_times_test():
  #given
  number_guesser = NumberGuesser()
  previously_chosen_numbers = [1,2,5]
  number_guesser.numbers_were(previously_chosen_numbers)
  #when
  guessed_numbers = [number_guesser.guess() for i in range(0,100)]
  #then
  for guessed_number in guessed_numbers:
    assert guessed_number in previously_chosen_numbers, 'every guess should be one of the previously chosen numbers'
  assert len(set(guessed_numbers)) > 1, "It shouldn't always guess the same number."

• 초기에 [1,2,5] 로 학습하고, 추가로 0 을 학습하였을 때, 예측 값은 [0,1,2,5] 중에서 존재해야한다.

  • 또한 충분히 수행된 예측값은 항상 같은 값일 수 없으므로, 예측값이 여럿이어야한다.
  • 실패 확률이 0은 아니지만 0에 수렴

• $N$개 데이터세트에서 복원추출 $k$회에서 모든 결과가 동일할 확률은

  • $P(\text{모든 추출이 동일한 항목일 확률}) = \frac{1}{N^k}$ 이므로
  • $P = \frac{1}{3^{100}} \approx 1.94 \times 10^{-48}$

def given_a_starting_set_of_observations_followed_by_a_one_off_observation_test():
    #given
  number_guesser = NumberGuesser()
  previously_chosen_numbers = [1,2,5]
  number_guesser.numbers_were(previously_chosen_numbers)
  one_off_observation = 0
  number_guesser.number_was(one_off_observation)
  #when
  guessed_numbers = [number_guesser.guess() for i in range(0,100)]
  #then
  for guessed_number in guessed_numbers:
    # 예측 범위는 추가로 학습된 0 도 포함해야한다.
    assert guessed_number in previously_chosen_numbers + [one_off_observation], 'every guess should be one of the previously chosen numbers'
  # 충분히 여러번 수행된 예측 값들은 항상 같은 결과를 가져오면 안된다.
  assert len(set(guessed_numbers)) > 1, "It shouldn't always guess the same number."

• 충분히 많은 테스트를 했다면, 모든 예측값이 다 나올 것이라는 테스트

  • 실패 확률이 0은 아니지만 0에 수렴

• 책에서는 실패 확률은 $0.5^{100}$ 로 추정하였으나, 3개 값 중 복원 추출하는 것이므로 포함-배제의 원리 Inclusion-Exclusion Principle 로 접근해야함

  • $\left| \bigcup_{i=1}^n A_i \right| = \sum_{k=1}^n (-1)^{k+1} \sum_{1 \le i_1 < \cdots < i_k \le n} \left| A_{i_1} \cap \cdots \cap A_{i_k} \right|$

  • $P(\text{모든 경우의 수가 다 나오지 않을 확률}) = \sum_{i=1}^{N} (-1)^{i+1} \binom{N}{i} \left(1 - \frac{i}{N}\right)^k$

  • $7.38 \times 10^{-18}$ 로 매우 작아 0에 수렴하는 것은 동일

def given_a_one_off_observation_followed_by_a_set_of_observations_test():
  #given
  number_guesser = NumberGuesser()
  print(number_guesser._guessed_numbers)
  previously_chosen_numbers = [1,2]
  one_off_observation = 0
  number_guesser.number_was(one_off_observation)
  number_guesser.numbers_were(previously_chosen_numbers)

  # # 예측 범위는 추가로 학습된 0 도 포함해야한다.
  all_observations = previously_chosen_numbers + [one_off_observation]
  
  #when
  guessed_numbers = [number_guesser.guess() for i in range(0,100)]
  
  #then
  for guessed_number in guessed_numbers:
    # 예측 값은 예측 범위 내에서 존재해야.
    assert guessed_number in all_observations, 'every guess should be one of the previously chosen numbers'
    
  # 예측값 3개 범위에서 100회 수행했으므로 모든 예측값이 존재하는지 테스트 (실패 확률이 0은 아니지만 0에 수렴)
  assert len(set(guessed_numbers)) == len(all_observations), "It should eventually guess every number at least once."

• 번외) 포함-배제의 원리로 모든 예측값이 나오지 않을 확률 계산해보기

import math

def probability_not_all_cases_appear(N, k):
    """
    Calculate the probability that not all cases appear at least once
    in k draws with replacement from N distinct items.
    
    Parameters:
    N (int): The number of distinct items.
    k (int): The number of draws.
    
    Returns:
    float: The probability that not all items appear at least once.
    """
    probability_not_all = sum(
        (-1) ** (i + 1) * math.comb(N, i) * (1 - i / N) ** k for i in range(1, N + 1)
    )
    return probability_not_all

# Example usage
N = 3
k = 100
print(probability_not_all_cases_appear(N, k))

머신러닝에 TDD 적용

• 각 ML 알고리즘이 가지는 정략적 측정 방법을 활용
  • 선형 회귀 분석 linear regression 은 adjusted R2 (조정된 결정계수)
  • 분류 분석 문제는 ROC curve (Receiver operating characteristic), confusion matrix 등
  • k-fold cross validation 도 많이 사용됨
    • k 개로 등분하여 subset 으로 여러 데이터세트 만드는 기법
    • 여러 데이터세트로 검증, overfitting 검증, 제 3의 데이터셋으로 검증
• 알고리즘이 좋다/나쁘다 기준이 아님. 가능한 좋은 모델을 찾기 위한 방법.

개선된 분석 모델의 검증 방법

• supervised learning 의 성능은 ROC curve 값을 사용 가능
  • AUC (Area Under the ROC Curve) : ROC curve 아래쪽 전체 영역의 면적
  • inflection point (변곡점) 위치를 파악
  • 전체 시간 비율에 따라 제대로 분류되어야하는 데이터의 최대치 설정

$\text{TPR} = \frac{\text{TP}}{\text{TP} + \text{FN}}$ , $\text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}$

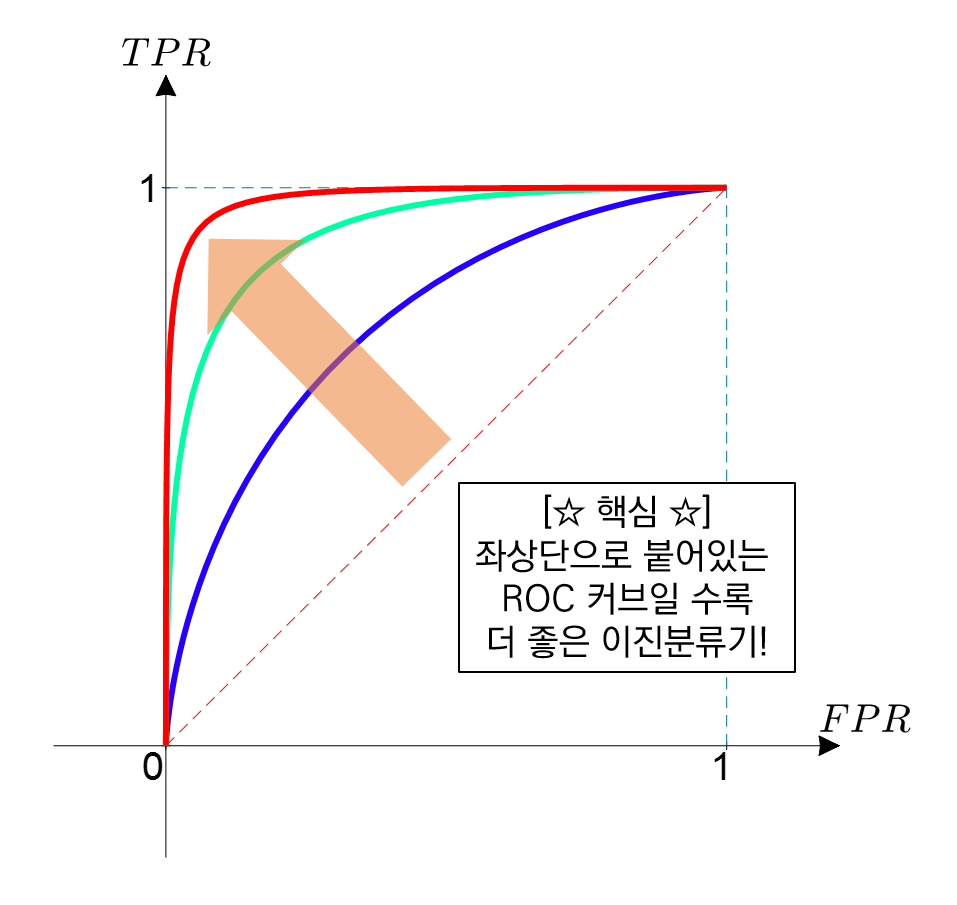
• 단, 분류기 성능이 좋다고 매출로 직결되진 않는다.
  • ex) 특정 광고를 잘못 내보냈을 때 소송비용이 크다면?
    • -> $FPR$ 이 높아질수록 (=광고 잘못 내보낼수록) 급격하게 순이익 감소

• unsupervised learning 은 cross-validation 기법을 통해 테스트
  • 이전 테스트의 학습 결과가 지속되지 않기에, 최종 결과가 좀 더 나은 객관성을 갖는다.

reference

• 서적 '테스트 주도 머신 러닝'
• Dan North BDD 소개
• 예제 코드 github