♣ 안녕하세요! 오늘 AI-REMEMBER는 원래 하는 노드 + 지난 포스팅에서 언급한 대로 14.12~14.14절의 AI의 현재와 미래, 머신러닝과 딥러닝 관련 내용을 어느 정도 더 다루겠습니다.
♣ 사실 Exploration 3이 아직 3일 정도의 시간이 남아있어서 남아있는 Fundamental 노드를 조금씩 채워가는 방향으로 가 보려고 합니다.
♣ 오늘 다루는 내용은 Fundamental 14장의 12절부터 14절까지 내용과, 당일 노드인 Fundamental 16장(선형 회귀, 로지스틱 회귀)입니다.
14장 'AI의 현재와 미래' 부분 요약 정리
- 머신러닝 상황에서는 더 좋은 모델을 만들기 위해 사람의 개입을 굉장히 필요로 한다.
- 머신러닝 모델을 학습시키기 위해서 데이터를 전처리하고 멋지게 가공하는 작업이 필수적이다.
- 다양한 파라미터들을 조합 또는 조절해서 더 좋은 피처를 만들어내어 모델의 성능을 높이는 과정을 피처 엔지니어링(Feature Engineering) 이라고 한다. 머신러닝에서는 이것이 내용이 방대한 부분은 있으나 매우 중요하다.
- 반면, 딥러닝은 모델의 복잡성을 늘려서 피처 엔지니어링을 최소화한다.
- 딥러닝은 뚜렷한 형태를 갖지 않은 데이터로부터 표현을 추출해내는 부분에 있어서 머신러닝보다 월등하다.
- 딥러닝 기반으로 자연어를 입력받아 기계번역을 하거나, 문장을 생성하는 Task 등을 수행할 수 있다.
- 직선 또는 평면의 형태로 정의되는 러닝 모델을 특별히 선형모델이라고 한다. 선형모델은 가장 단순한 러닝모델이다.
- 오늘날 이미지 인식 분야에서는 선형모델을 쓰지 않는다. 이미지 데이터는 픽셀로 구성되어 있기 때문에 복잡한 구조와 특성을 가지므로 선형모델로 표현하고 반영하는 것이 어렵기 때문이다.
- 이미지 인식 분야에서는 선형모델에 대한 대안으로 인공신경망과 같이 복잡성이 높은 러닝 모델을 이용한다. 복잡성이 높은 신경망의 구조를 러닝모델로 사용하는 머신러닝 패러다임을 딥러닝이라고 한다.
- 퍼셉트론은 합성함수로 볼 수 있다.
- 퍼셉트론은 입력층, 은닉층, 출력층으로 크게 3개의 층으로 이루어진다.
- 다층 퍼셉트론에서는 은닉층의 개수가 많을수록 인공신경망이 Deep하다고 한다. 이렇게 충분히 깊은 인공신경망을 러닝모델로 사용하는 머신러닝 패러다임을 딥러닝이라고 한다. 여기서 충분히 깊은 인공신경망을 다른 말로 심층 신경망(DNN)이라고 한다.
- 컨볼루션 신경망은 이미지 인식 분야에서 많이 사용한다.
- 순환 신경망은 자연어 처리 분야에서 많이 사용한다.
- 딥러닝 모델의 효과적인 학습을 위해서는 상당히 많은 데이터를 필요로 한다.
- 딥러닝은 연산량이 매우 높아 학습에 걸리는 시간이 오래 걸리는 경우가 많다.
- 머신러닝/딥러닝 모두 예측하거나 출력한 결과가 어떻게 도출되었는지 설명할 수 있어야 신뢰도를 높일 수 있다.
16.1 회귀(Regression)
- Regression Analysis : 관찰된 여러 데이터를 기반으로 각 연속형 변수 간의 관계를 모델링하고 이에 대한 적합도를 측정하는 분석방법으로, 단순히 평균으로 수렴하는 현상을 넘어서서 2개 이상의 변수 사이의 함수관계를 추구하는 통계적인 방법
- Linear Regression : 두 변수 사이의 관계를 직선의 형태로 가정하고 분석하는 방법
- Linear Regression에서 좋은 모델을 만들기 위해 필요한 4가지 기본가정
- 선형성 : 종속변수와 독립변수 간에 선형성을 만족하는 특성을 의미
- 독립성 : 다중 회귀분석 시에 중요한 기본가정이 되는 특성으로 독립변수들 간에 상관관계 없이 독립성을 만족하는 특성을 의미
- 등분산성 : 분산이 같다는 것을 의미. 분산이 같다는 것은 어느 한쪽으로 데이터가 치우치지 않고 고르게 분포한다는 의미. 등분산성의 주체는 잔차(Residuals)이다.
- 정규성 : 잔차가 정규성을 만족하는지 즉, 잔차가 정규분포를 보이는지의 여부를 의미
- 분류와 회귀의 차이점
- Classification(분류) : 주어진 데이터의 여러 특성값들을 이용, 해당 데이터의 클래스를 추론하는 방법
- Regression(회귀) : 주어진 데이터의 여러 특성값들을 이용, 해당 데이터와 연관된 다른 데이터의 정확한 값을 추론하는 방법
- 분류모델은 클래스를 추론하기 위해 클래스별 확률 값을 출력한다.
- 회귀모델은 연관된 종속변수의 값을 직접 출력한다.
16.2 Linear Regression 더 자세히 알아보기
- 선형 회귀는 종속변수 y와 하나 이상의 독립변수 x와의 선형 상관관계를 모델링하는 회귀분석 방법이다.
- 독립변수가 1개일 경우 단순 선형회귀, 2개 이상일 경우 다중 선형회귀라고 한다.
- 선형회귀식 y=βx+ϵ에 대한 고찰
- β : 회귀계수
- ϵ : 오차 (모집단의 회귀식에서 예측된 값과 실제 관측 값의 차이)
- β, ϵ은 모두 파라미터이다. 이는 우리가 데이터로부터 추정해야 하는 값이다.
- x, y에 해당하는 데이터가 있을 때 이러한 데이터로부터 파라미터를 추정한 뒤 그 값들을 바탕으로 모델링을 한다.
- 선형회귀 모델을 찾는다는 것은 주어진 데이터에 선형 식이 잘 맞을 수 있도록 회귀계수 및 오차를 구하는 것이다.
- 머신러닝의 선형회귀모델 : H=Wx+b
- W : 가중치(Weight)
- b : 편향(bias)
- H : 가정(Hypothesis)
- 딥러닝 기법을 이용해서 회귀모델을 구한다는 것은, 결국 주어진 데이터를 활용해서 파라미터 W와 b를 구하는 것을 말한다.
- W, b는 대개 스칼라 값이라기보다는 Matrix 형태로 나타나는 경우가 많다.
- 파라미터의 개수가 많아질수록 모델의 크기가 커지므로 학습도 어려워진다.
- 잔차(Residuals) : 표본집단의 회귀식에서 추정한 값과 실제 데이터 간의 차이
- 최소제곱법 : 잔차를 이용하여 주어진 점 데이터들을 가장 잘 설명할 수 있는 회귀모델을 찾는 대표적인 방법
- 최소제곱법의 사용 : n개의 점 데이터에 대해 잔차의 제곱의 합을 최소로 하는 W, b를 구하는 것이다.
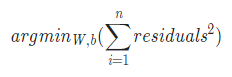
- 결정계수(R-squared, R2 score) : 0에서 1 사이의 값을 가지며 1에 가까울수록 회귀모델은 데이터를 잘 표현하고 있다는 해석이 가능하다.
- 해당 회귀그래프 해석
- R2 Score 값이 0.544이지만, LSTAT가 커질수록 price는 작아지므로, LSTAT과 price 사이에는 음의 상관관계를 갖는다.
- 점 데이터가 결정된 회귀직선 근방에 대체로 잘 모여 있다.
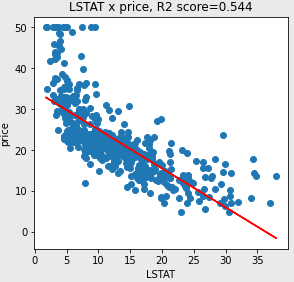
- 경사하강법(Gradient Descent)
- 적절한 회귀모델의 회귀계수를 찾기 위해서는 손실함수 설정을 잘 해야 한다.
- 머신러닝에서는 가중치의 Gradient 즉, 미분값이 최소인 지점을 손실함수를 최소로 하는 지점일 것이라고 가정한다.
- 일반적인 가중치 함수는 아래로 볼록한 모양을 띤다.
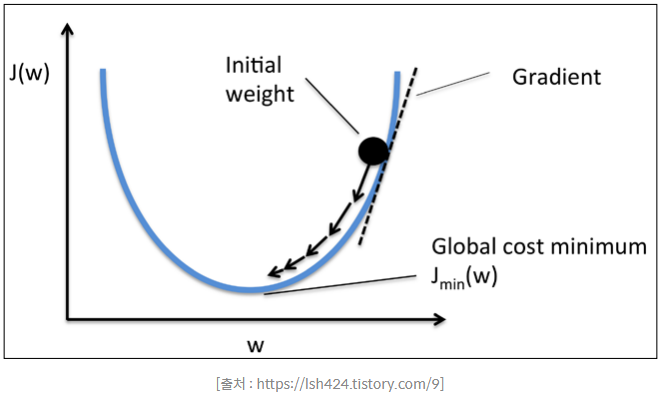
- 그림의 'Global cost minimum'을 만족하는 가중치 값을 가지려면 Gradient 즉, 기울기 값이 가장 작아지는 시점인 중앙에 위치하면 된다.
- 최소지점으로 가기 위해 Gradient 값을 업데이트하는 공식
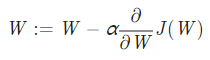
- 공식에서 α는 learning rate를 의미한다.
- α의 값이 클수록 화살표의 길이는 길어지며, 더 빠르게 수렴하는 지점으로 갈 수 있다.
- learning rate는 적당히 커야 한다. 너무 크게 될 경우 가중치 값을 건너뛰며 진행하는 상황이 생기면서 수렴하지 못할 수 있기 때문이다.
- 이러한 적절한 learning rate를 설정하는 것은 머신러닝/딥러닝에서 매우 중요하다.
16.3 로지스틱 회귀분석(Logistic Regression)
- 데이터가 어떤 범주에 속해있을 확률을 0에서 1사이의 범위에서 예측을 하고, 예측한 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도학습 알고리즘이다.
- Y값은 확률을 나타낸다. 따라서 Y의 하한과 상한은 각각 0과 1이다.
- 1개 이상의 독립변수를 이용하여 데이터가 2개의 범주 중 하나에 속하도록 결정하는 이진 분류 문제를 풀 때 사용한다.
- Sigmoid Function은 아래의 로지스틱 회귀식을
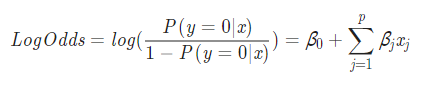
P(Y=0∣x)에 대해 정리한 식에 대하여
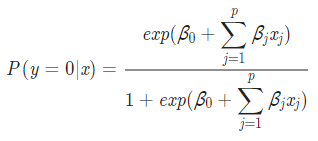
지수함수 자체를 z로 치환하여 우변을 간단히 하였을 때,
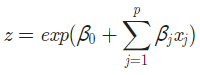
아래와 같이 정리할 수 있다. 이것을 시그모이드(Sigmoid) 함수라 한다.
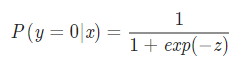
- P(Y=0∣x) : 독립변수 x에 대하여 종속변수 y의 값이 0일 확률
- 로지스틱 회귀문제를 해결하는 순서
- 실제 데이터(x)를 대입하여 Odds와 회귀계수(β)를 구한다.
- Odds 구하는 방법 : 사건이 발생할 확률을 그렇지 않을 확률로 나눈 값이다.
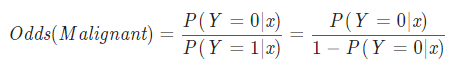
- Odds는 (0,∞) 사이의 값을 갖는다.
- LogOdds를 계산하고, 계산한 값을 시그모이드 함수의 입력으로 넣는다.
- 특정 범주에 속할 확률의 값을 계산한다.
- 설정한 한계점(Threshold)에 대하여 그 값 이상이면 1, 아니면 0으로 이진분류한다.
- 로지스틱 회귀는 분류모델이라기보다는 회귀모델로 본다. 그 이유는 모델이 리턴하는 값이 연속적인 변수로 나타나기 때문이다.
- 다만 분류 문제를 확률적으로 접근하기 위한 아이디어를 제공하는 모델이 될 수 있다.
16.4 Softmax Function, Cross Entropy
- 로지스틱 회귀는 이진 분류뿐만 아니라 셋 이상의 여러 범주로 분류하는 다중 로지스틱 회귀로 확장될 수 있다.
- 셋 이상의 범주를 분류할 때에는 시그모이드 함수가 아닌 Softmax 함수를 사용한다.
- Softmax 함수식은 아래와 같으며, 아래와 같은 특징을 갖는다.
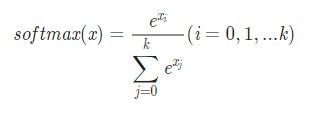
- 각 범주의 확률 값은 0에서 1 사이의 값을 가진다.
- 모든 범주에 해당하는 softmax의 값의 총합은 1이다.
- softmax 함수에 모든 범주의 LogOdds를 통과시켰을 때, 해당 데이터가 어떤 범주로 분류되는지 확실히 알 수 있도록 하기 위해, 가장 크게 나온 값만 1을 부여하고 나머지 값은 모두 0을 부여하는 one-hot encoding 방식을 활용하게 된다.
- Cross Entropy 함수식은 아래와 같으며, 구성 및 특징은 다음과 같다.
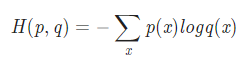
- Softmax 함수의 Loss Function이다.
- 가중치가 최적화될수록 H(p,q)의 값이 감소하는 방향으로 가중치 학습이 된다.
- p(x) : 실제 데이터의 범주 값
- q(x) : Softmax의 결과 값
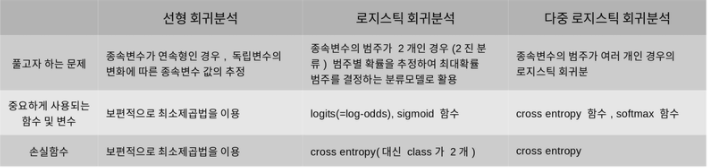
<최종 정리>