Clustering(군집분석)이란?

유사한 속성들을 갖는 데이터를 일정한 수의 군집으로 그룹핑하는 비지도 학습입니다.

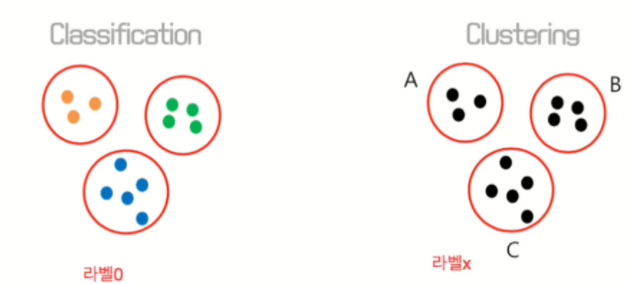
지금까지 다루었던 머신러닝 모델(선형회귀, 다중선형회귀, 결정트리)는 특정 독립변수에 대한 종속변수(레이블, 정답)이 있는 경우입니다. 하지만 클러스터링의 경우는 정답이 없는 경우에 사용하며 속성별로 데이터를 나누게 됩니다. 때문에 몇개의 군집으로 나누어질지는 분석하는 입장에서 알 수 없다는 특징을 가집니다.

Clustering의 목표

좋은 군집화란 동일한 군집에 속한 데이터들 서로 유사하게 그룹핑하는 것입니다. 다른 의미로는 다른 군집에 속한 데이터들이 서로 다를수록 좋다는 뜻이 됩니다.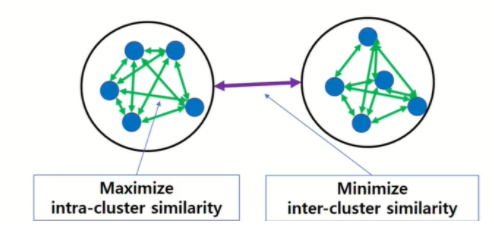

군집화 종류

• 분할적 군집화(Partitional Clustering)
• 계층적 군집화(Hierarchical Clustering)
• K-평균 군집화(K-Means Clustering)

분할적 군집화

특정 기준에 의해 동시에, 각 데이터들을 미리 정해진 개수의 군집 중 하나로 할당 시키는 군집화 방법입니다.

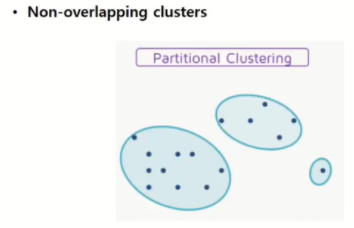
계층적 군집화

가까이에 위치한 (유사한) 데이터들끼리 계층적으로 결합(agglomerative) 시켜 나가는 방식으로 데이터들이 결합되는 과정을 나타내는 dendrogram을 생성합니다. 이 방법은 사전에 군집 개수를 지정하지 않는 방법으로 결정트리의 가지치기와 유사하며 원소 단위부터 데이터를 결합시킵니다.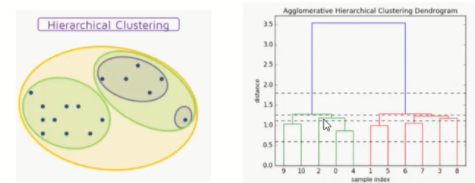

K-평균 군집화(K-Means Clustering)

K-평균 군집화란 대표적인 분할적 군집화 알고리즘으로 사전에 군집의 수(K)를 지정합니다.

각 군집은 하나의 중심점 (centroid, center)이 존재하고 각 데이터들을 가장 가까운 중심점에 해당하는 군집에 할당하는 방식입니다.

K-평균 군집화 알고리즘은 다음과 같습니다.

1.구하고자 하는 군집의 수(K) 설정
2.초기 데이터의 분포 상태에서 K개의 중심점을 임의로 지정
3.각 데이터들로부터 K개의 각 중심점 까지의 거리를 계산
4.각 데이터들을 가장 가까운 중심점이 속한 군집에 할당
5.K개의 중심점을 다시 계산하여 갱신 ( 중심점은 각 군집의 데이터들의 평균값)
6.중심점이 더 이상 변하지 않을 때까지 3, 4, 5 과정을 반복

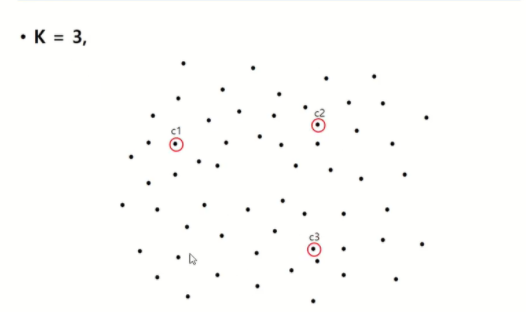
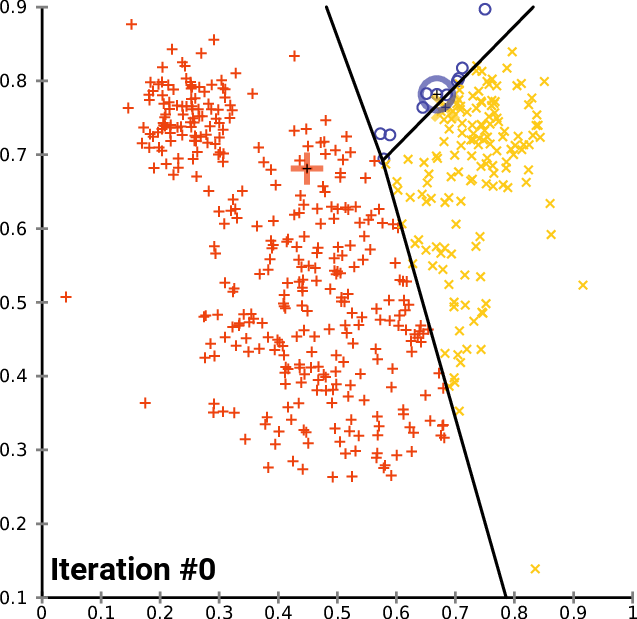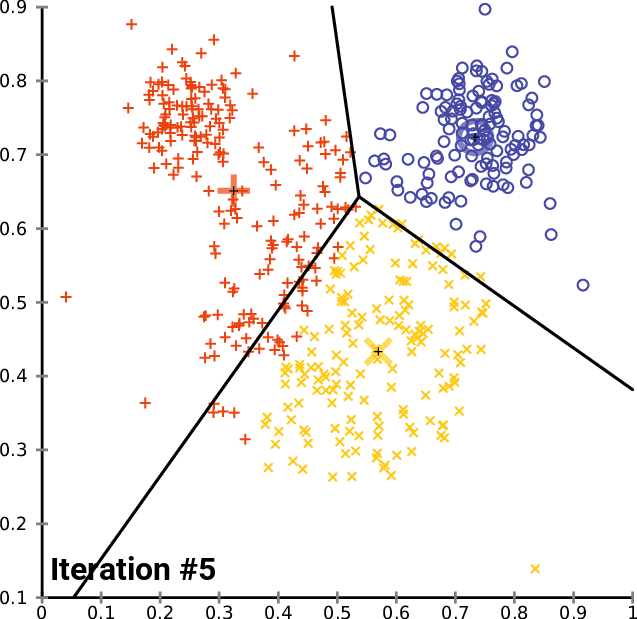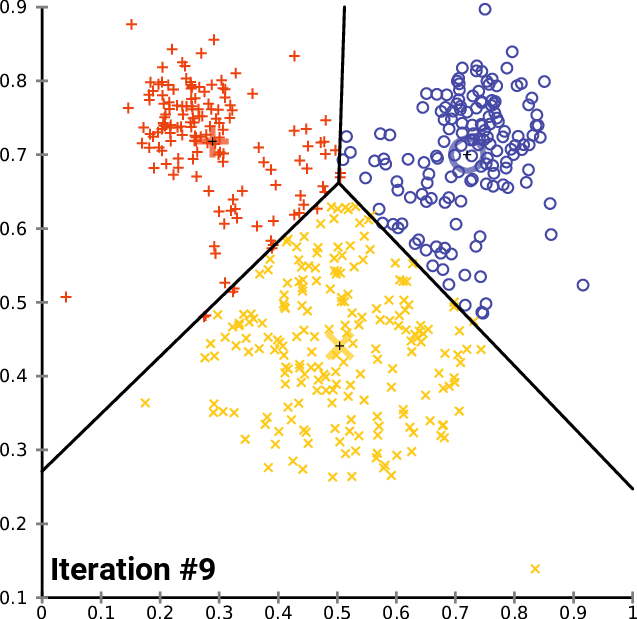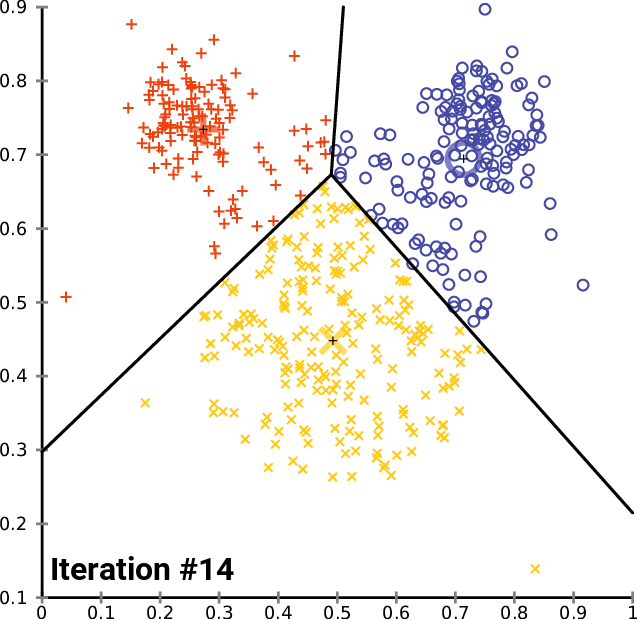
K(군집의 수)를 3으로 지정하고 임의의 점 c1, c2, c3를 지정합니다.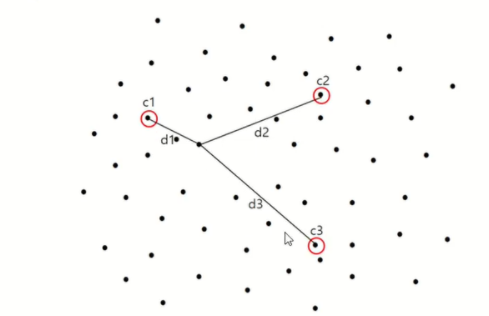
그 이후 모든 원소에 대해서 c1, c2, c3까지의 거리 중 가장 가까운 우너소에 군집을 할당합니다.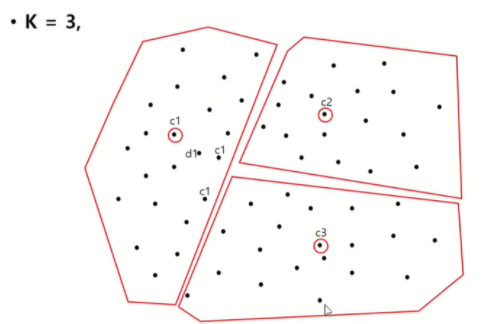

이 과정을 반복하고 나눠진 그룹 안에서 평균에 해당하는 점을 찾습니다.

모든 점들로부터의 거리(오차)의 합이 가장 작아지는 점을 찾고 모든 점에 대해 반복하면서 더이상 옮겨지지 않는 c1, c2, c3를 찾는 것이 최종 군집이 됩니다.

초기 중심점의 중요성

초기에 임의로 정해지는 k개의 중심점에 따라서 결과가 달라질 수 있습니다.

군집화 고려사항

군집화는 거리(유사도) 계산 방식을 사용합니다.

Euclidean, Manhattan, Pearson correlation, Mahalanobis .... 등 다양한 거리 계산 방식이 존재합니다.

사용하는 거리 계산 방식에 따라 군집화 결과가 달라질 수 있습니다.

군집화 결과의 평가는 객관적 평가 지표에 따릅니다.

Sum of Squared Error(SSE), Silhouette coefficient ....

거리 (유사도) 계산 방식

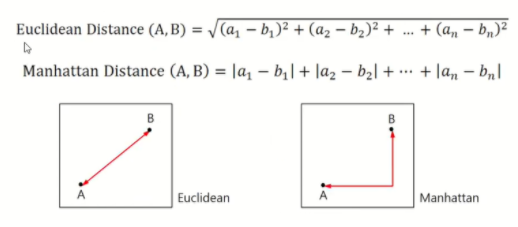
일반적으로 사용하는 거리 계산 방식으로는 Euclidean Distance를 사용합니다.

군집화 결과의 평가

• Sum of Squared Error(SSE)

군집 분석의 기본 목적에 충실한 방법이지만 군집 내의 거리만을 고려한다는 단점이 존재합니다.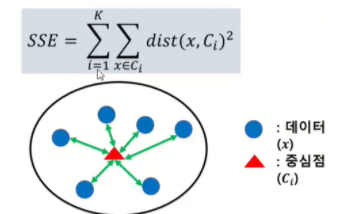

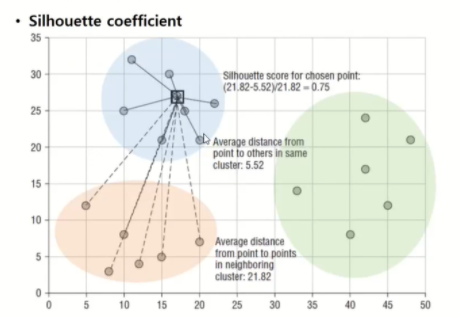
• Silhouette coefficient

a(i): 데이터 i 로부터 같은 군집 내에 있는 다른 모든 데이터들 사이의 평균 거리:

클러스터 내의 응집이 덜된 정도(a(i)값은 작아질수록 성능향상)

b(i): 데이터 i로부터 가장 가까운 인접 군집 내에 있는 데이터들 사이의 평균 거리 중 가장 작은 값:

클러스터 간의 분리도(b(i) 값은 커질수록 성능향상)

-1 에 가까울수록 나쁜 결과이고 1에 가까울수록 좋은 결과

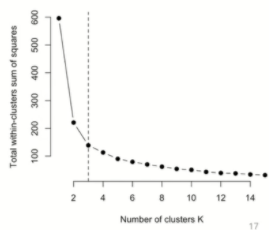
군집 개수(K)의 설정

많은 경우에는 몇 개의 군집이 적정한지를 사전에 알고 있습니다. 하지만 그렇지 않은 경우 평가 지표를 이용하여 최적의 군집 수를 선택하게 되는데 이는 Elbow point에서 결정하게 됩니다.

• X축 : 클러스터 개수

• Y축 : 클러스터 내 오차제곱합(SSE)
  

  요약

• 비지도 학습 방법으로서 탐색적 데이터 분석(EDA) 단계에 활용 가능합니다.

군집 내는 최대한 유사하게, 군집 간은 최대한 이질적으로 군집을 구성하는 것이 군집화의 목표입니다.

K-평균 군집화의 경우 분할적 방법으로 사전에 정해높은 군집의 개수대로 군집화를 진행합니다.

한가지 주의 사항으로는 K-평균 군집화는 모든 변수들의 거리를 계산하기 때문에 모든 변수가 수치형 변수인 경우에만 사용이 가능합니다.