1. Multiclass

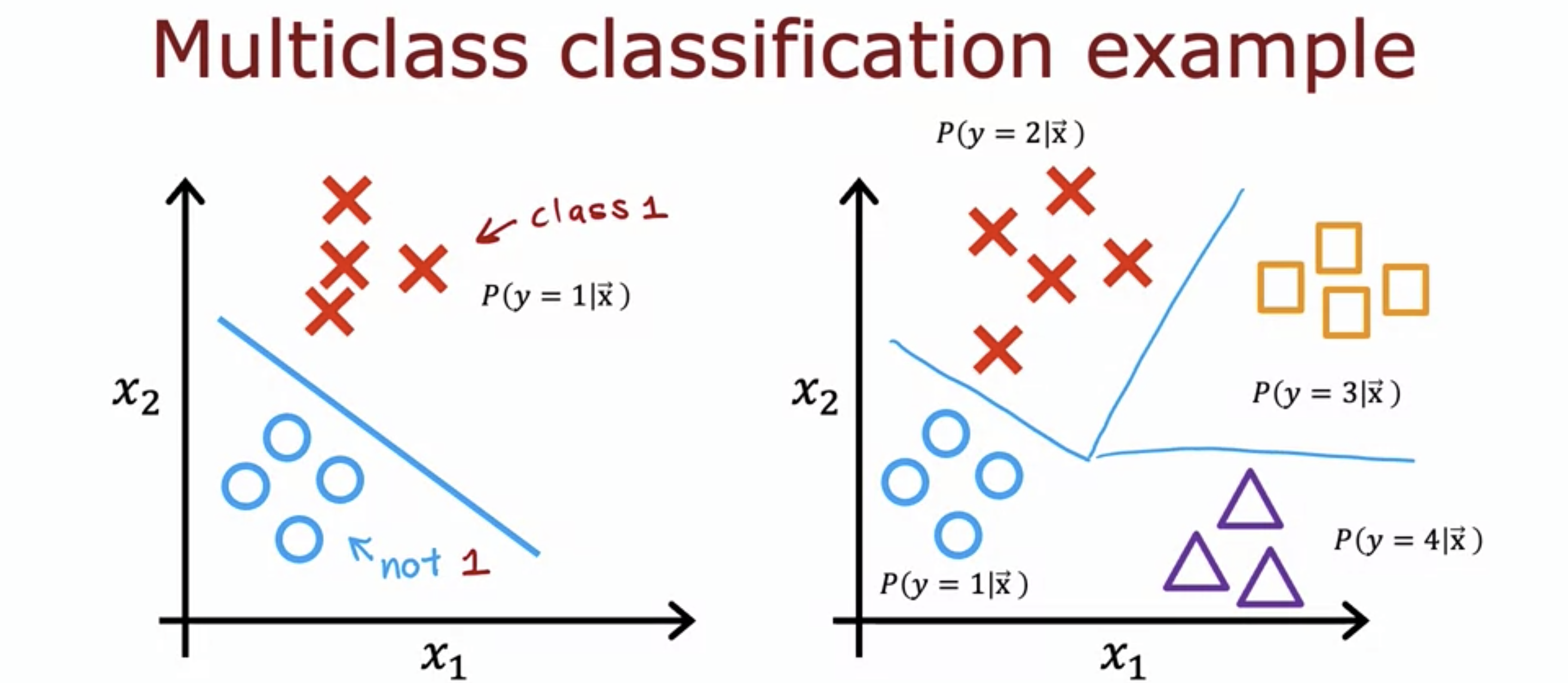
• No more binary classification, now more categories.

2. Softmax

• Softmax is a generalization of logistic regression in order to address classification of multiclass outputs.
• In the video, the softmax is used for classifying the hand-written digit from 1-9.

Loss Function for Softmax

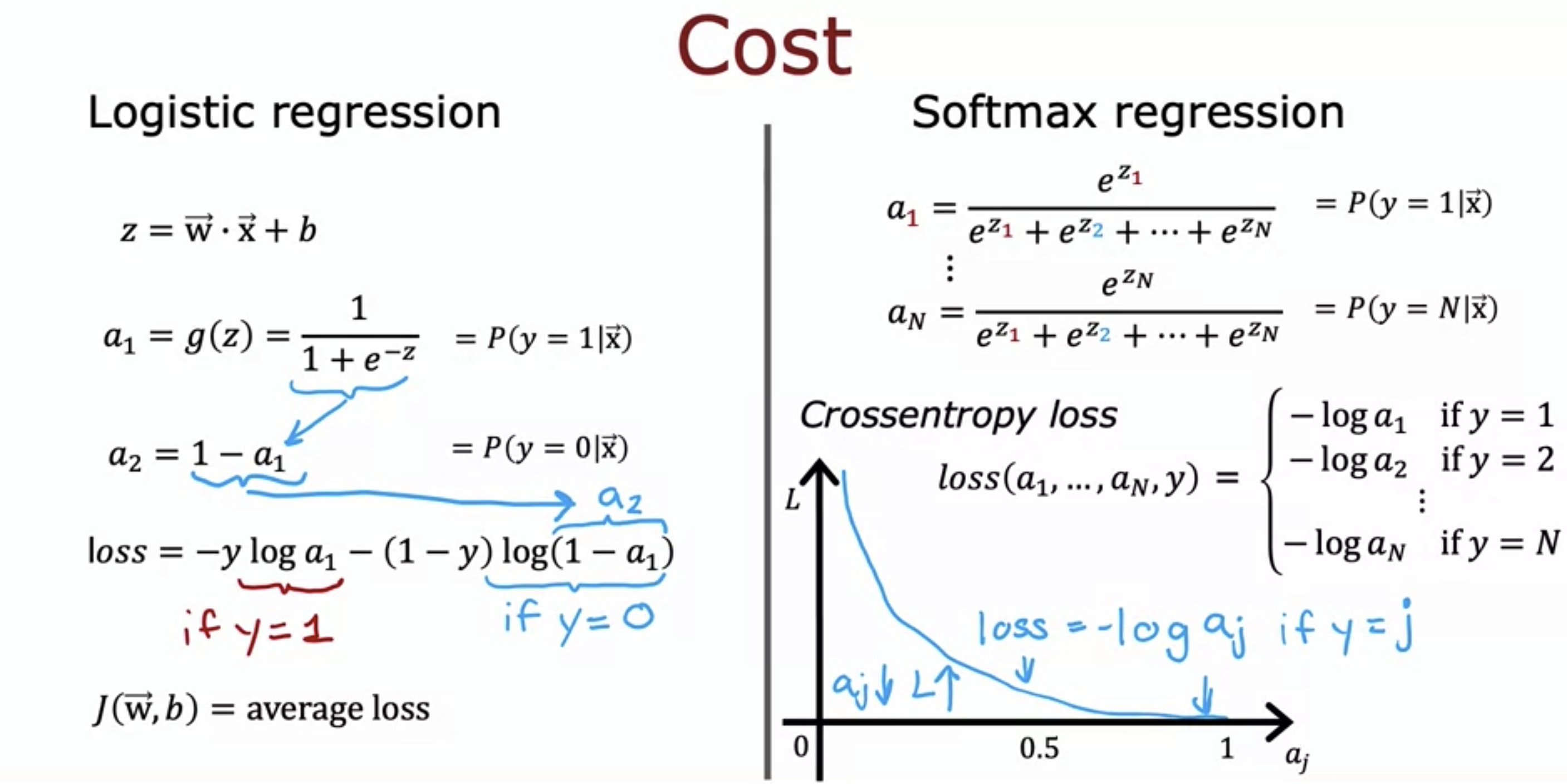
• As the probability of it being a_j gets closer to 1, the cost decreases to 0.
  
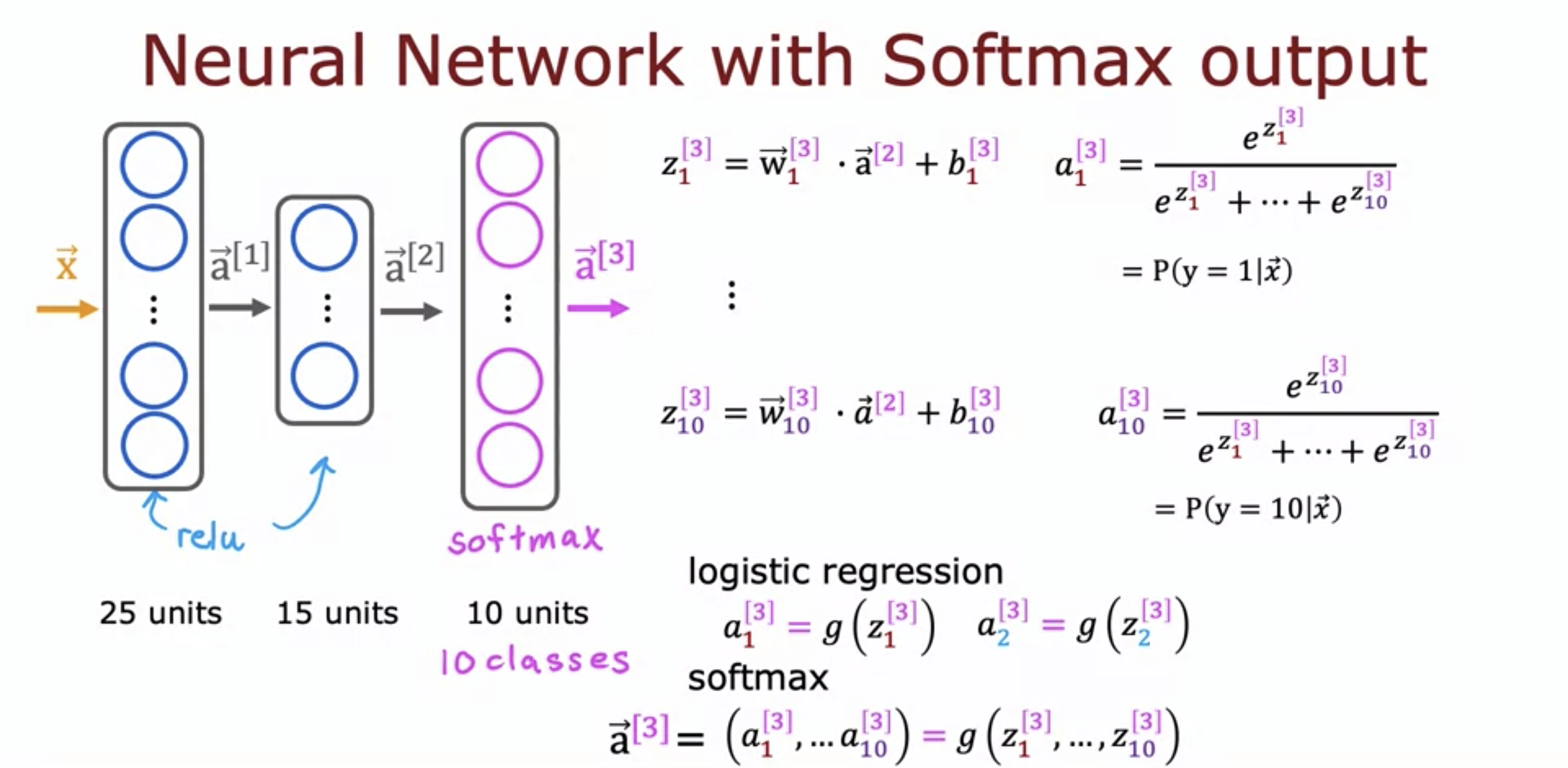
• Unlike other activation functions, softmax depends on z values of other neurons.

• SparseCategoricalCrossentropy - sparse for only one possible output instead of several
• There is a better way tho...

Cost Function of Softmax

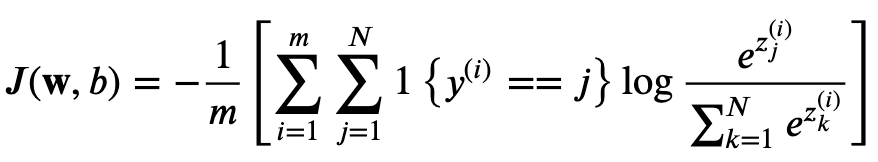
• m is the number of examples,
• N is the number of units,
• i is the i-th example,
• j is the j-th unit, as well as the j-th class for classification.

3. Improved Implementation of Softmax

• In logistic regression, instead of using g(z) as an intermediate value for the loss function, we could expand it - this would give more accurate value for the loss.
• The original compile function call is changed with the addition of from_logits=True and the change of activation function of the last layer from sigmoid to linear.

• New function tf.nn.softmax(logits) is used together to predict.

4. Multi-label Classification

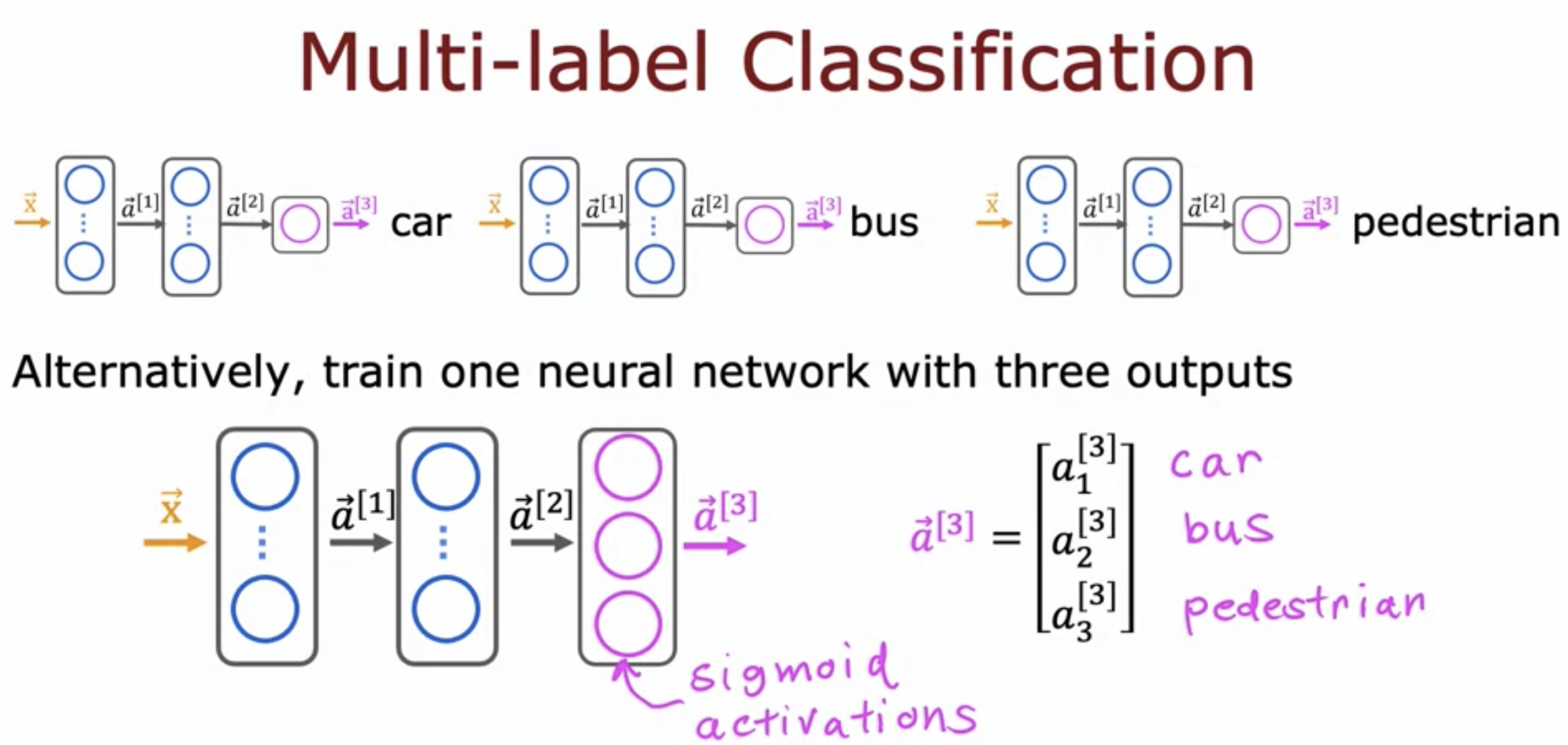
• Each output in the final layer represents the probability that there is a car, there is a bus, and there is a pedestrian.
  • These probabilities do not add up to 1, because each is different label.
  • In multi-class classification, the probabilities do add up to 1.
  • To sum up, multiclass classification is classifying categories that are related to one another, while multi-label need not be.