1. Diagnosing bias and variance

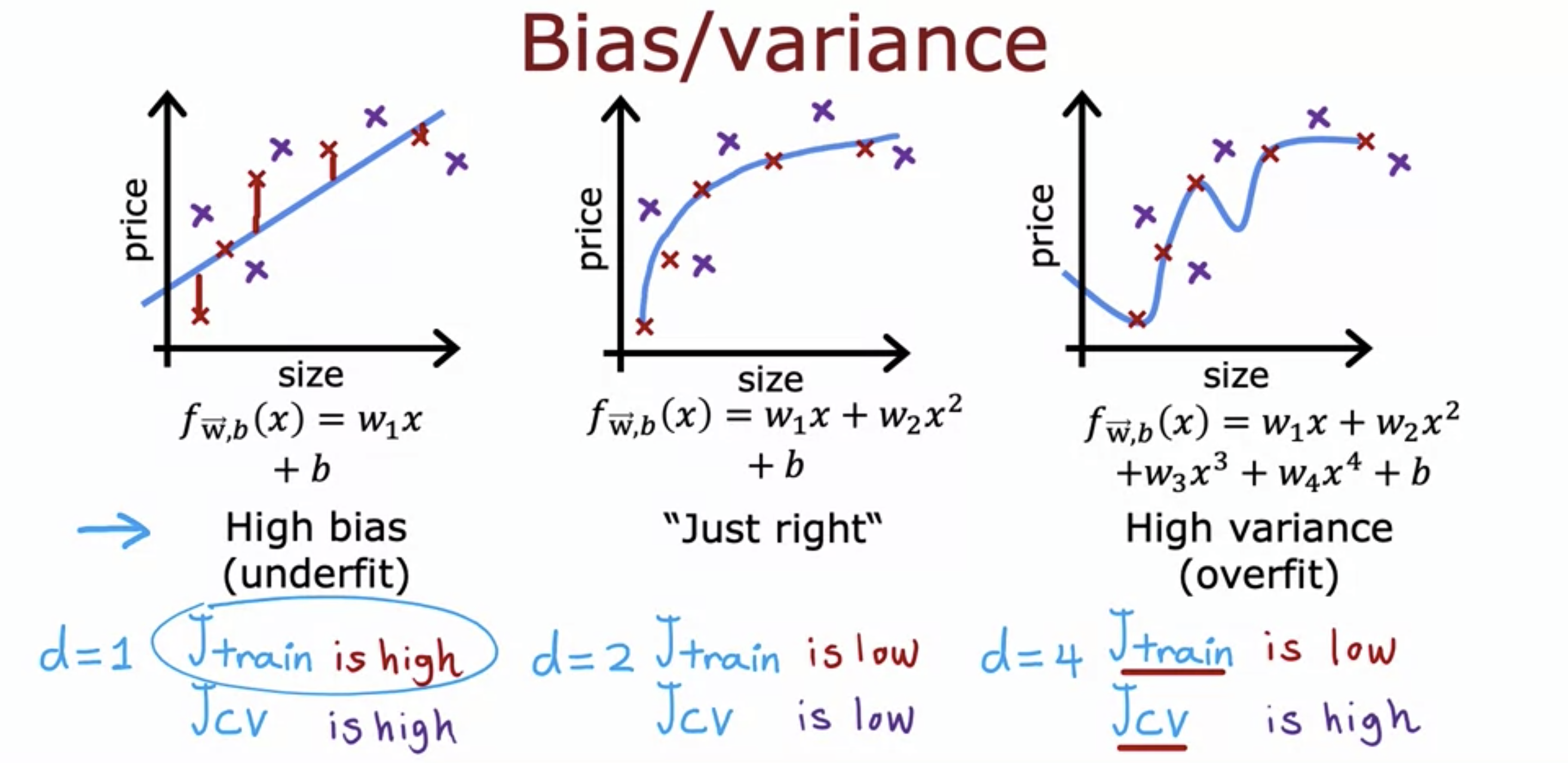
• High bias means the model is too simple to capture the complexity of the underlying data.
  • Both J_train() and J_cv() are high.
• High variance means the model is too complicated
  • J_train() is low, but J_cv() is high.
• Both Js are low for an ideal model.

• In worst case it is possible to have both high bias and high variance.

2. Regularization and bias/variance

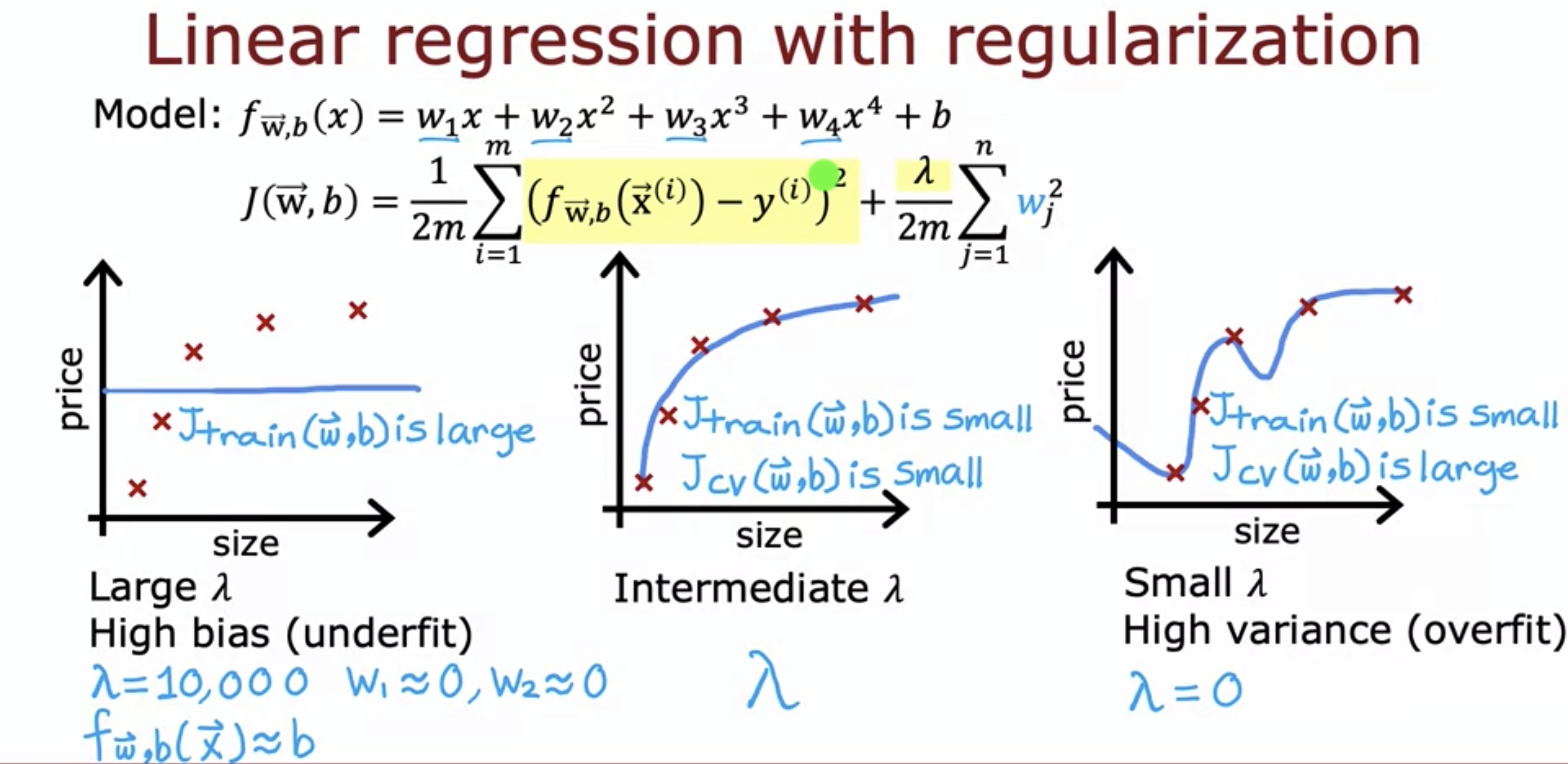
• A large lambda value of the regularization term can lead to high bias, whereas a small lambda value leads to high variance.
• Choosing a good lambda value is important for a good model.

• Just like how we did for cross-validation set, we try different lambda values and pick the lambda value that leads to the least J_cv() value.
• Then we report generalization error using test set.

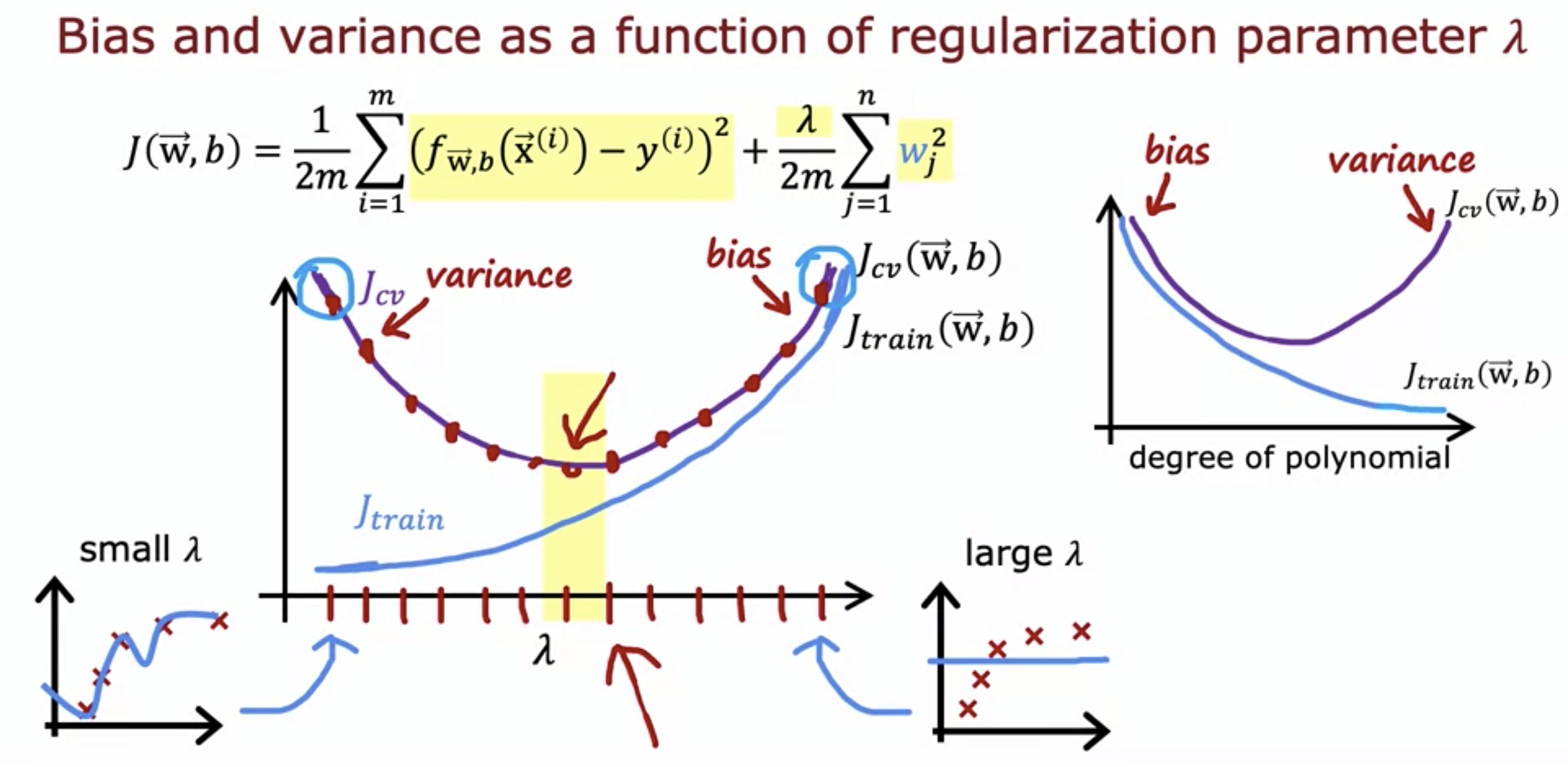
• As seen from the graph above, J_train() is low and J_cv() is high (high variance, overfitting) when the lambda is low, because low lambda means no penalties to the parameters.
• and both J_train() and J_cv() are high (high bias, underfitting) when lambda is high, because high lambda means high penalties to the parameters, making the model a straight line.

3. Establishing a baseline level of performance

• High training error does not always mean that the algorithm is doing badly.
• When assessing a model for speech recognition, for example, it is good to have a human level performance measured as well.
• By comparing human level performance and training error, we can see that the model is actually not that bad.
• One reason why the model shows high training error could be because the inputs are inaudible in the first place, as proven by the low human level performance as well.

• If the difference between baseline performance and the training error is higher than the difference between training error and CV error, the model has high bias (underfitting).
• If its the otherwise, the model has high variance (overfitting).
• If the training error is close to the baseline performance, it means the algorithm is doing decently.

4. Learning Curves

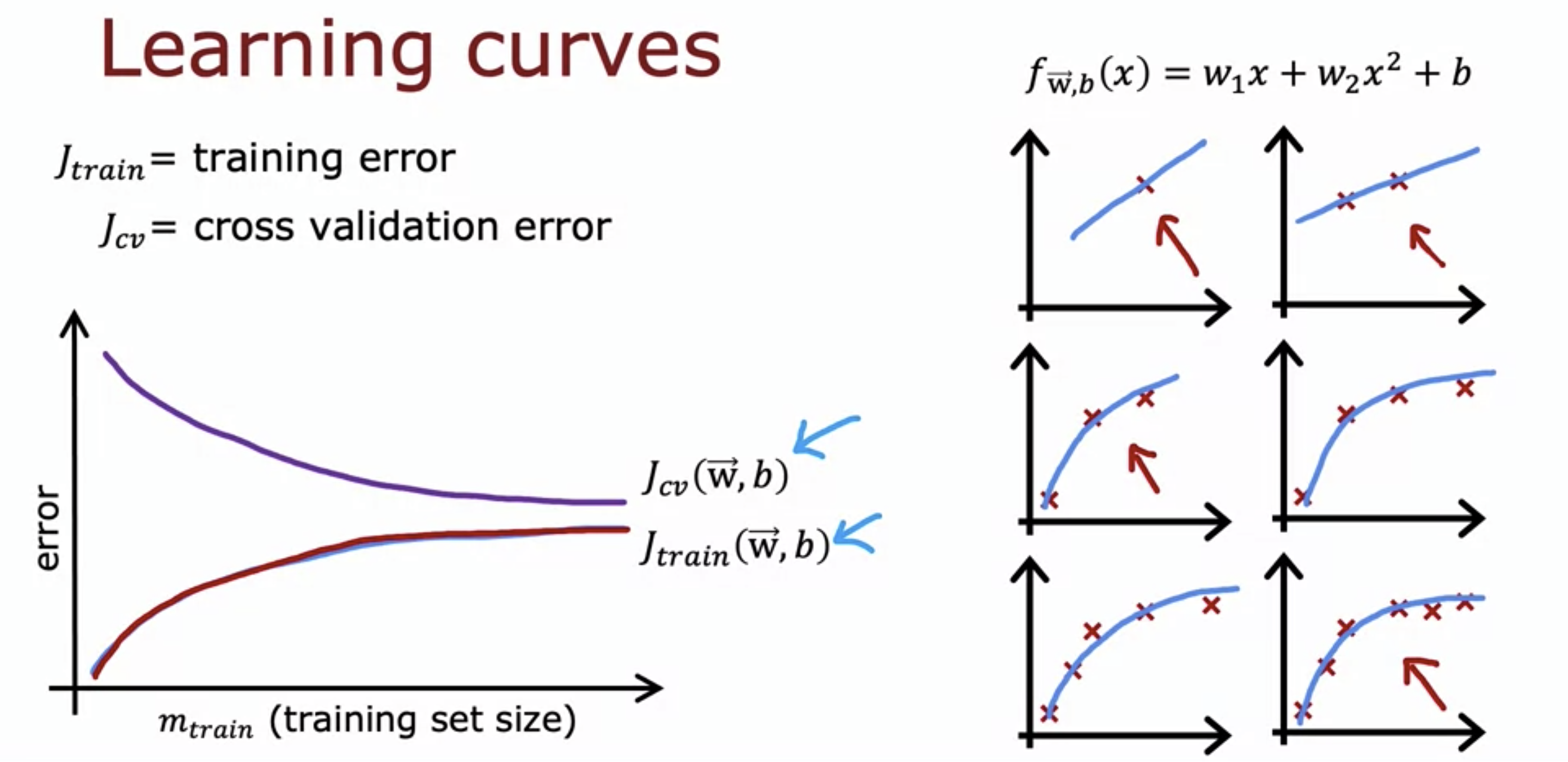
• J_train() is lower than J_cv() all the time.
• As more data is collected, their learning curves flatten out.

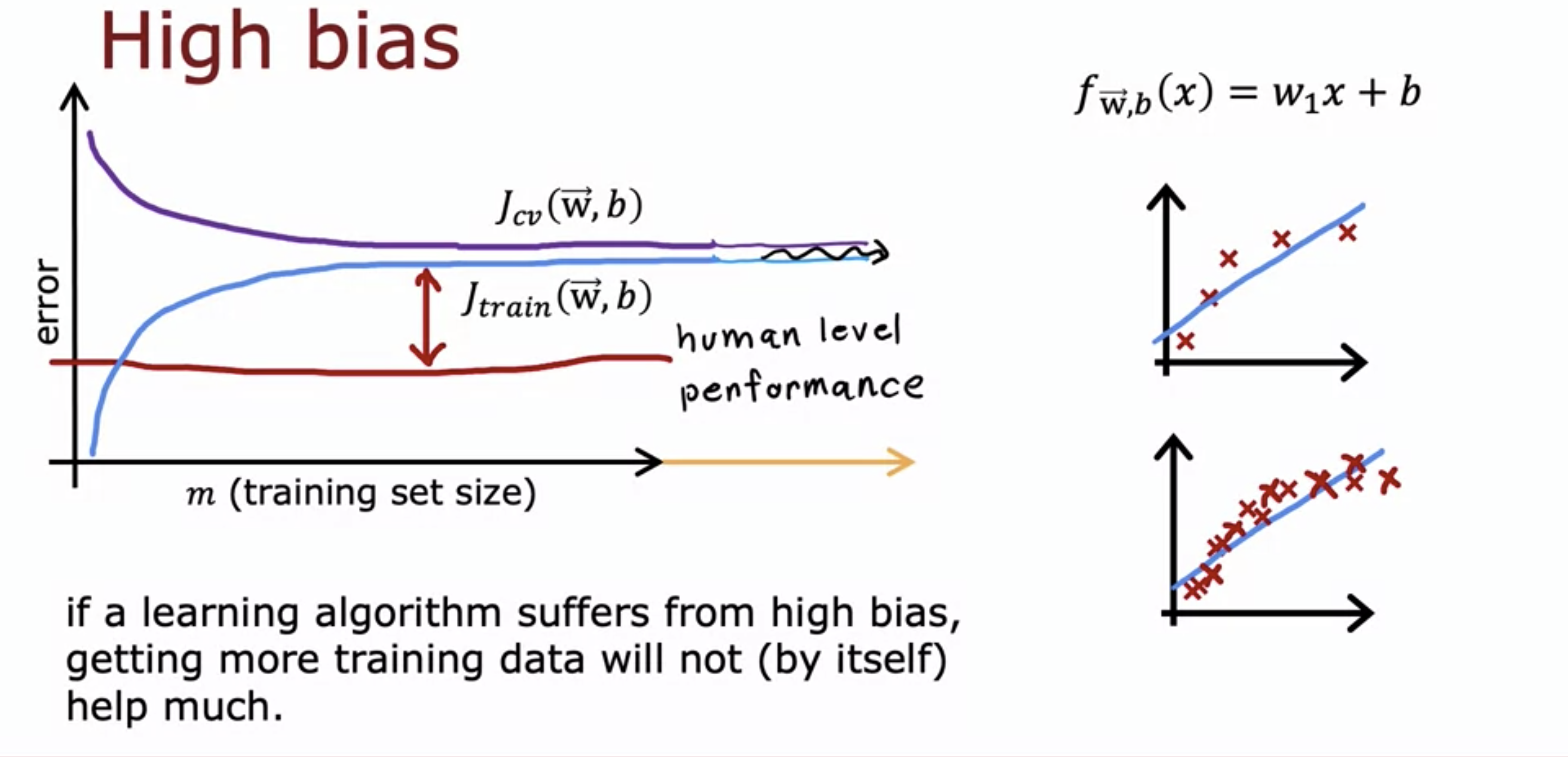
• For a model with high bias, collecting more data does not really help lowering the error down to baseline level performance.
• This is because a model with high bias is too simple that it lacks the capacity to learn from the existing data.

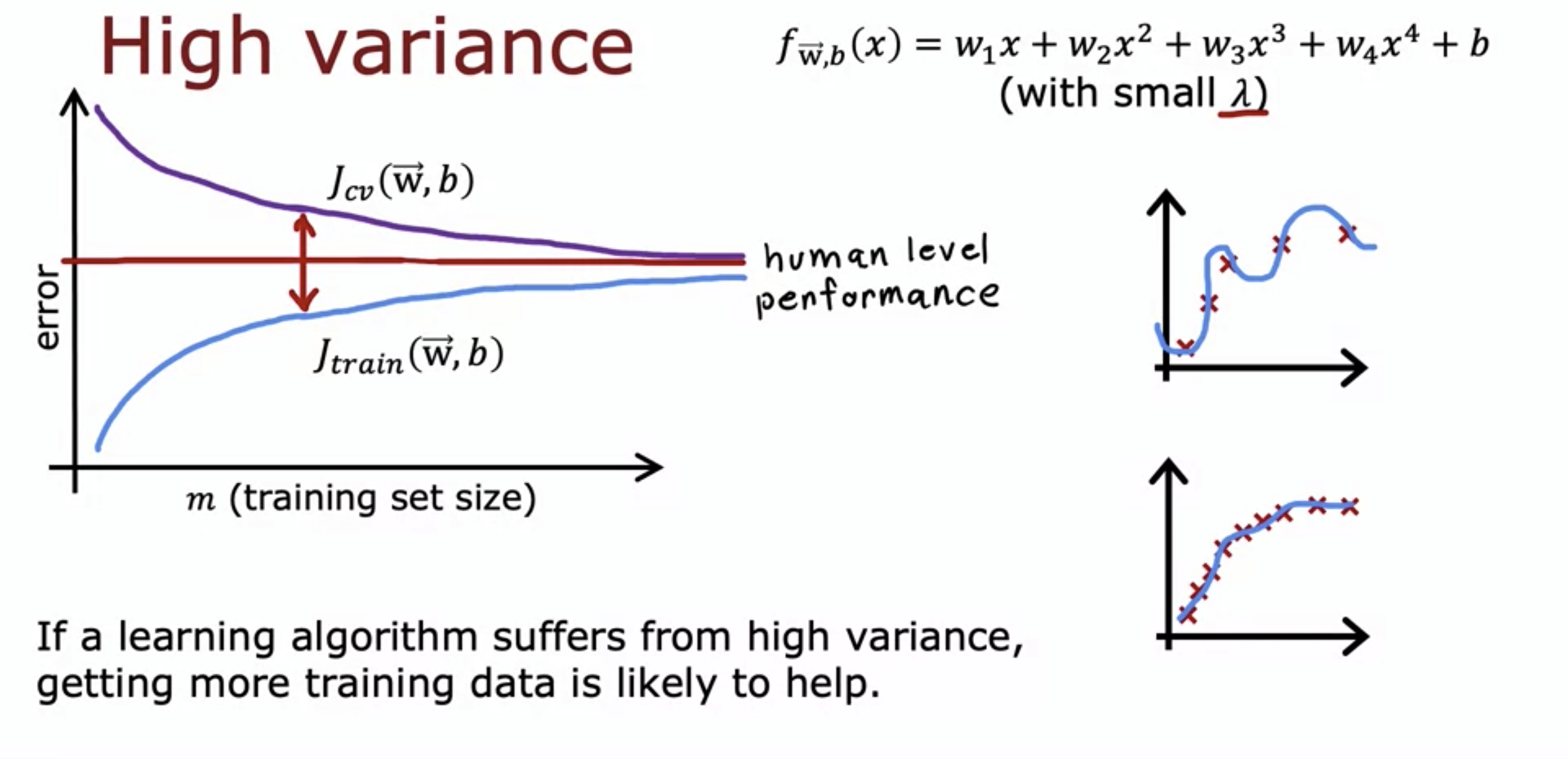
• For high variance models, J_cv() is much much higher than J_train() with small training set size.
  • This is because of the noise in the data. With little data, 4th degree polynomial could be too complicated that it overfits the data.
• When training set size is small, J_train() is lower than human level performance, because of the overfitting.

5. Debugging a learning algorithm

• Bias vs Variance takes a very short time to learn but a life time to master - a standford phd student LOL

6. Bias/variance and neural networks

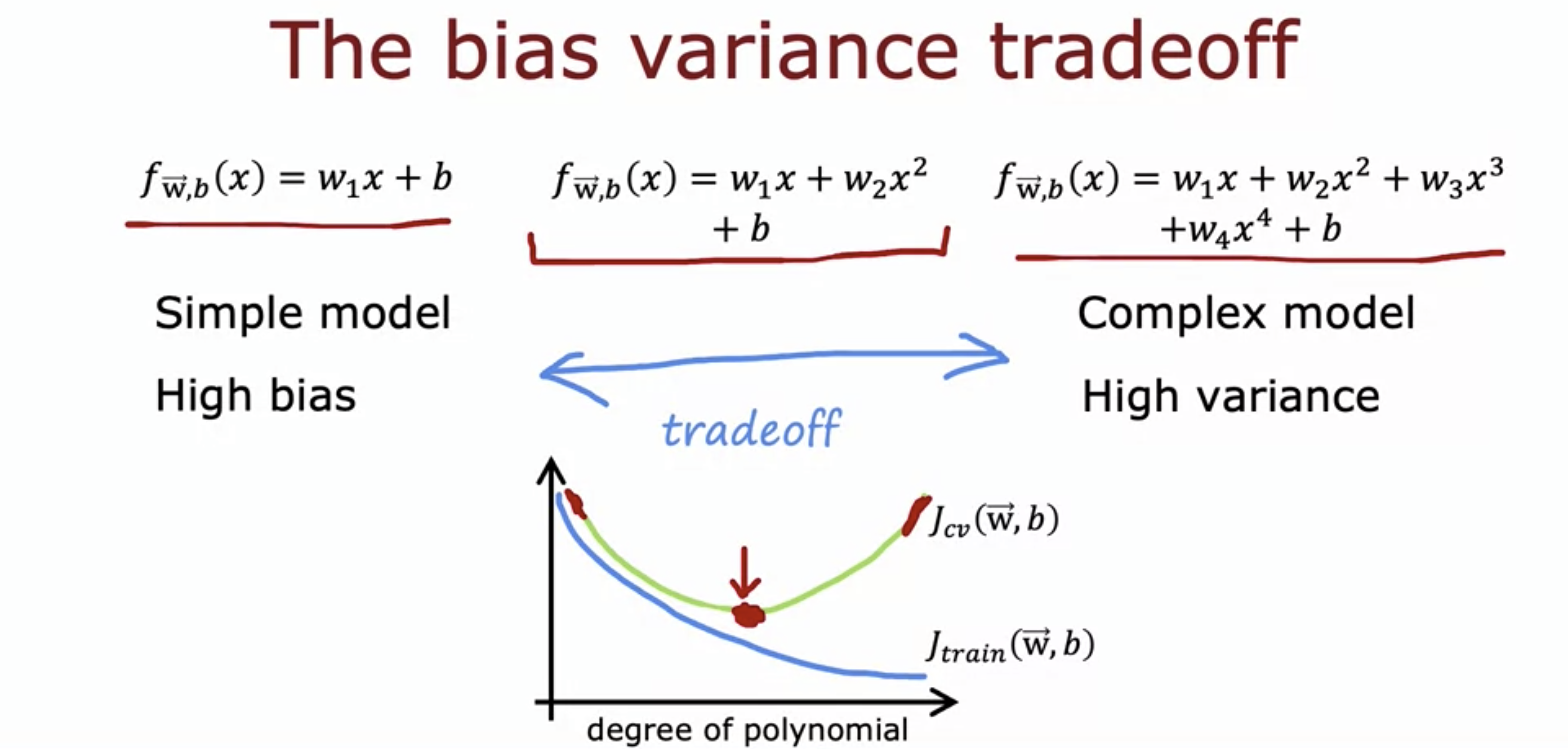
• It is usually the case that we need a tradeoff between bias and variance.
• However, for neural networks, we don't really need it.

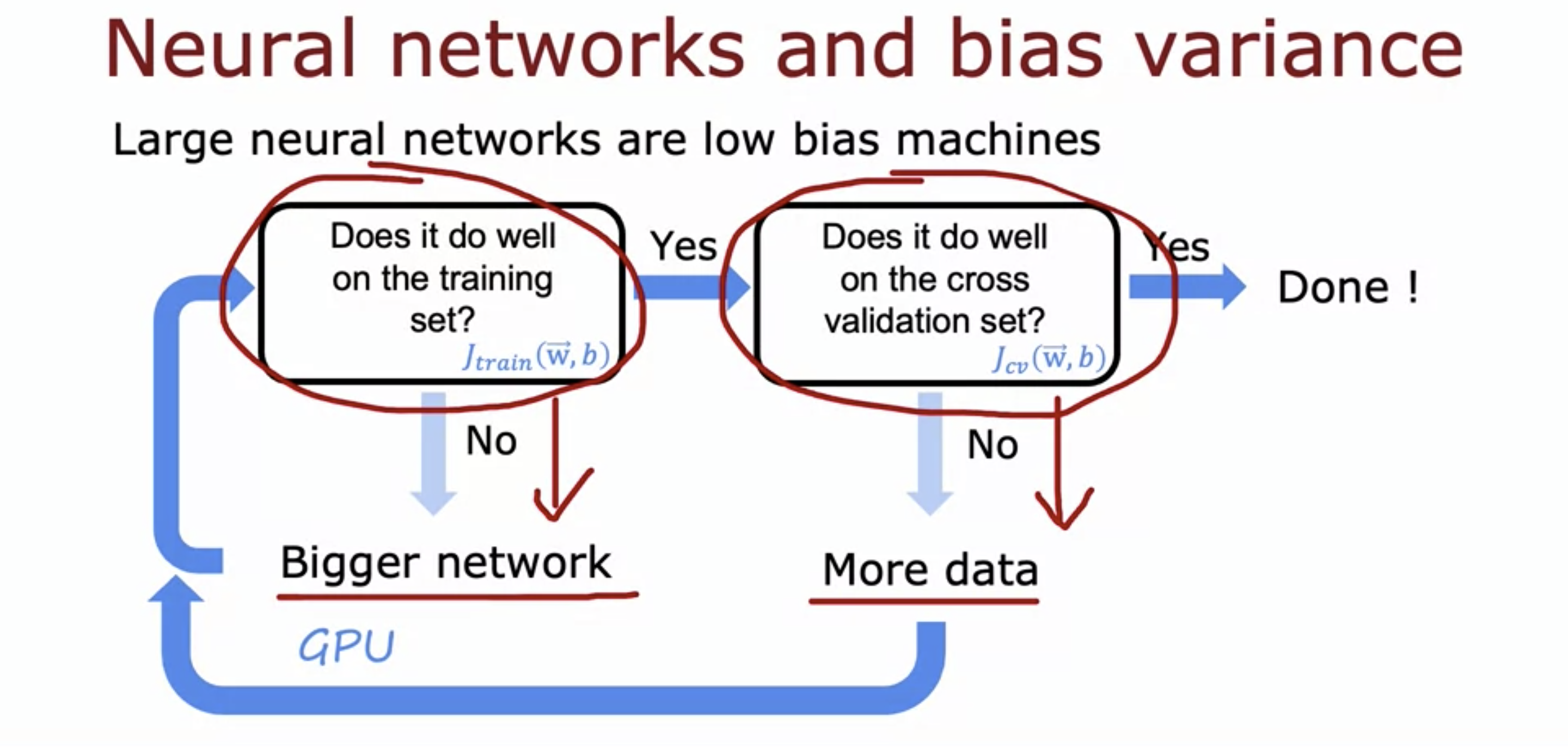
• Large neural networks are low bias machines.
  • If we make neural networks large enough, we can almost always fit our training set well, so long as our training set is not enormous.
• If J_train() is quite big, we can make a bigger network.
  • Bigger networks will solve high bias problems.
  • Bigger networks are of course more computationally expensive.
• If it is quite negligible, then if J_cv() is big, we can collect more data.

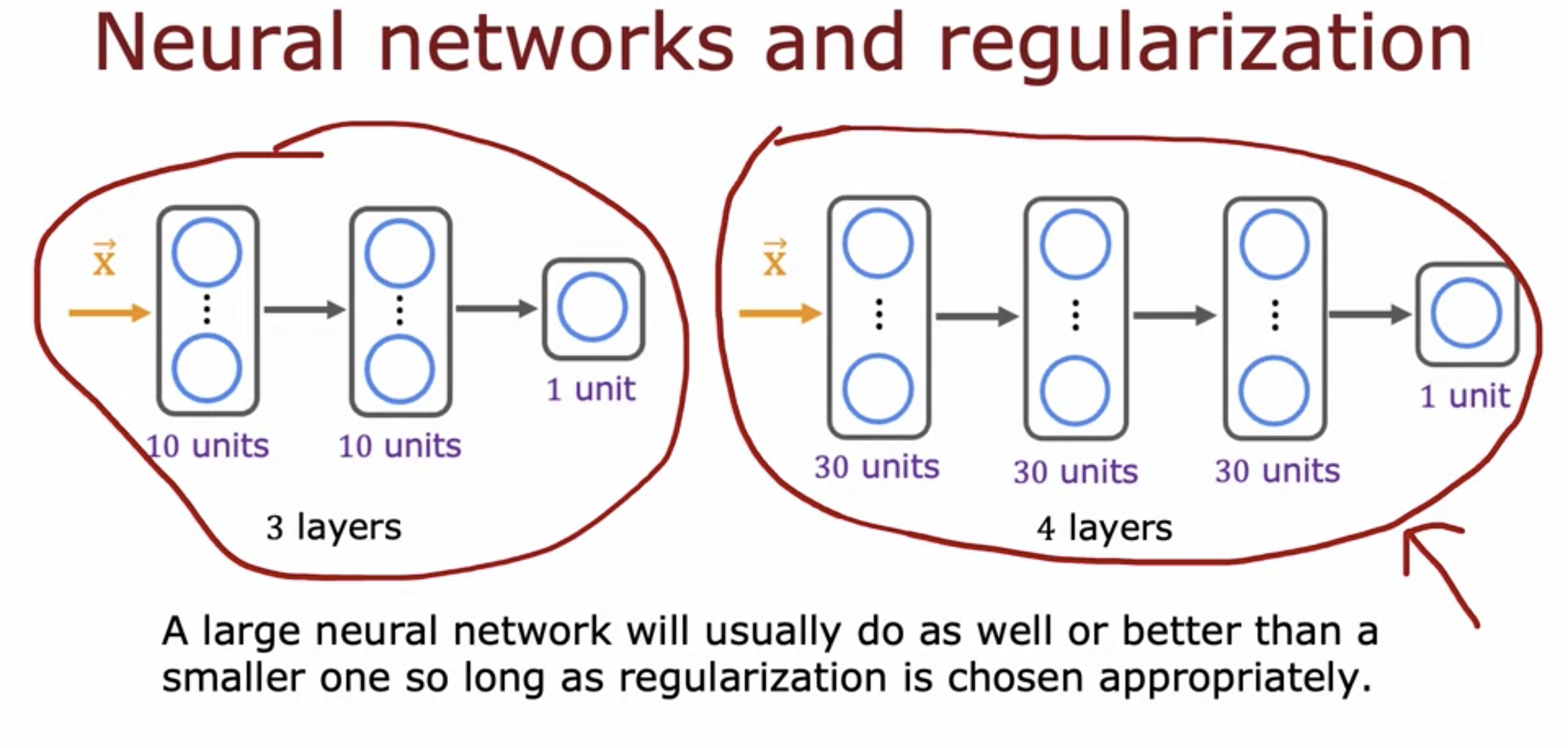
• So long as regularization term is chosen appropriately, it will not hurt to have a larger neural network.

• kernel_regularizer=L2(0.01) to add regularization term
  • 0.01 is thel lambda in this case