[AIB]Note121~2 Hypothesis Test, Chi-square test

1. Hypothesis Test

1.1 Hypothesis Test가 무엇인가?

• 가설검정이라고 한다. 데이터를 분석을 하고 '~~할 것이다.'라고 할 때 이러한 주장이 타당한지 아닌지를 확인하는 과정
• 우리가 알고 싶은 것은 '모집단'의 특성이다. 하지만 모집단의 특성을 정확하게 알기란 불가능이다. 이 때 필요한 게 일부분을 추출해서 그 일부분(=sample)을 통해 모집단의 특성을 유추한다.

1.2 모집단과 sample

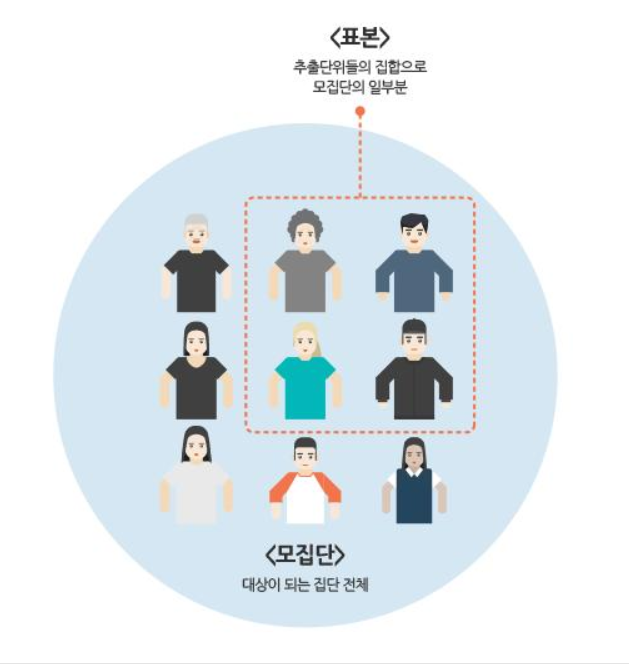사진 출처:통계청

1.2.1 모집단(Population)

• 정보를 얻고자 하는 대상이 되는 집단 전체.
• 모집단을 다 알 수 있을 거 같은데? 라는 생각이 들 수 있다. 대한민국 국민의 키, 학력 등등 이런 것을 정확하게 알기 위해서는 직접 조사하고 이를 분류하고 정리해야한다.
  그러기에는 시간, 노력 등등이 많이 필요하다. 또 대한민국 국민이 아니라 기업에서 (잠재)소비자을 모집단으로 정하면 알 수 없다. 이러한 여러 이유로 인해 모집단을 알아내는 것은 불가능으로 생각하면 된다.

1.2.2 표본(Sample)

• 모집단의 일부분
• 모집단을 정확히 알아내는 것은 불가능에 가깝기 때문에 모집단의 일부분인 표본을 통해 '모집단은 이럴것이다!'라고 추정하는 것이다.

1.2.3 샘플링(Sampling)

• 모집단에서 샘플을 추출하는 행위
• 단순 무작위 표본추출(Simple random sampling): 모집단에서 표본을 무작위로 추출하는 방법, 구체적으로는 모집단의 각각의 요소, 특징 등이 표본으로 선택될 가능성이 같게 된다.
• 계통 표본추출(Systematic Sampling): 표본을 추출 할 때에 규칙을 가지고 추출하는 방법, N번째의 표본을 추출한다라고 생각하면 된다.(3, 5, 7, 9 ... 번째의 데이터를 추출)
• 층화 표본추출(Stratified Random Sampling): 모집단을 미리 중복되지 않는 여러 그룹으로 나누고 각 그룹 별로 무작위로 추출하는 방법. 여론조사를 생각하면 좋다. 20~29세, 30~39세,,, 처럼 나이대별로 나누고 해당 나이대에 맞는 사람 중에서 무작위로 조사를 해서 표본을 추출하는 방법
• 군집 표본추출(Cluster Sampling): 모집단을 미리 여러 그룹으로 나누고, 이후 특정한 그룹을 무작위로 선택하는 방법.

+ 표본 평균의 표준 오차(Standard Error of the Sample Mean): 표본 통계량(sample의 값, 수치로 이해하면 쉽다)의 표준 편차를 의미한다.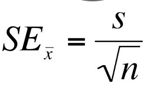
n은 표본의 수(Sample size), s는 표본의 표준편차(Sample standard deviation)이다. 여기서 알 수 있듯이, n(표본의 수)이 커질수록, 표준 오차는 줄어든다. 우리가 찾고자 하는 모수의 특성과 근사한 값을 얻을 수 있고, 높은 신뢰도를 바탕으로 모집단을 추정할 수 있게 된다.

1.3 평균과 표준편차(Standard deviation)

• 보통 많이 사용하는 것이 평균과 표준편차(or 분산)이 된다.
• 평균(Mean, m)은 산술 평균, 기하 평균 등이 있는데 여기서는 산술 평균, 즉 우리가 흔히 쓰는 평균이다.
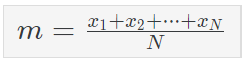  N은 표본의 수!
• 표준편차(Standard deviation)는 흩어져 있는 정도를 나타낸다. 즉, 표준편차가 작을수록 평균값에 많이 모여있고, 클수록 많이 떨어져있다.
  
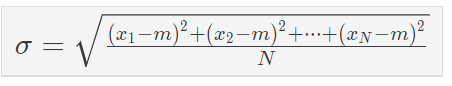
• 분산(Variance)는 표준편차를 제곱해주면 된다. 이말은 분산의 제곱근(루트)이 표준편차라는 뜻!
  

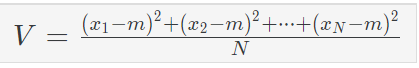
1.4. 귀무가설과 대립가설, 신뢰도, p-value

• 귀무가설(Null Hypothesis): 어떤 것 사이에는 차이가 없다고 하는 가설, 자연 상태 그대로의 가설,
  예) 두 집단 간의 평균 차이는 '없을 것'이다.
• 대립가설(Alternative Hypothesis): 통계검증을 하기 위해 세우는 가설, 귀무가설이 기각되면 채택하는 가설.
  예) 두 집단 간의 평균 차이는 '있을 것'이다.
• 신뢰도(Confidence level): 모수(알고싶은 모집단의 특징)가 신뢰구간 안에 포함될 확률 (보통 95%, 99% 등 사용) - N123때 신뢰구간으로 더 자세히 정리!
  예) 신뢰도가 95%다 = 모수가 신뢰 구간 안에 포함될 확률이 95% = 귀무가설이 틀렸지만 우연히 맞을 확률이 5%
• p-value(유의확률, p값): 주어진 귀무가설이 '얼마나 타당한지, 얼마나 근거가 있는지'를 0과 1사이의 값으로 표현해준다.
  0에 가까울수록 귀무가설의 설득력이 낮아진다.(=귀무가설을 기각하고 대립가설 채택).
  예) p-value = 0.000000000005, 귀무가설의 설득력이 낮으므로 귀무가설을 기각하고 대립가설을 채택한다. 보통 0.05나 0.01을 기준으로 삼는다.(근데 절대적인 것은 아님)

1.5 T-test

• 목적: 두 개의 표본(값)의 '평균' 같은지 다른지 비교하기 위해 사용한다.
• 언제: 샘플의 값이 정규성, 등분산성, 독립성을 만족할 때 사용한다.
  + 정규성 - 데이터가 정규 분포 할 때(아니면 Mann-whitney test), 등분상성 - 두 그룹이 유사한 분산 값을 가질 때(아니면 자유도 수정해서 다시 t검정), 독립성 - 두 그룹이 연결(paired)되어 있지 않은 상태(아니면 대응표본 t검정)

1.5.1 One Sample t-test

• 내가 수집한 데이터나 샘플을 통해 모집단의 평균이 특정 값과 같은지를 검증하는 방법
• 즉, 내가 가진 데이터의 평균이 얼마이고, 분산이 얼마인데, 이 데이터를 바탕으로 과연 모집단의 평균이 특정한 값이라고 말할 수 있는지를 검증할 수 있다.
• 귀무가설: 평균 = 특정값,
  대립가설: 평균 != 특정값

1.5.2 Two Sample t-test

• 서로 독립적인 두 집단의 평균이 차이가 0인지 확인한다. 즉 두 샘플의 평균이 같은지 비교.
• 귀무가설: 집단1의 평균 - 집단2의 평균 = 0,
  귀무가설: 집단1의 평균 != 집단2의 평균

2. Chi-square test

2.1 Type of Error

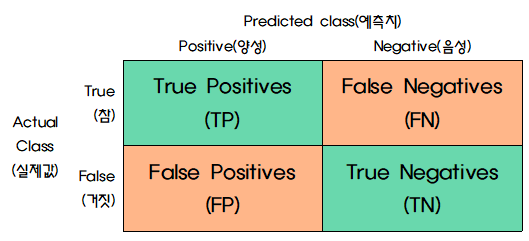
• 실제 값이 '찐이냐 아니냐'로 보고, 예측치가 '도구'를 사용해서 찐인지 아닌지를 판별한다고 이해하면 쉽다.
• Actual Class: '찐'으로 코로나에 걸렸다. 안걸렸다.
  Predicted Class: 자가진단 키트를 통해서 양성/음성으로 나타나는 것.
• TP/TN: '찐'으로 코로나 걸려서, 키트에서 양성으로 뜨는 것. '찐'으로 코로나에 안걸려서, 키트에서 음성으로 뜨는 것. -> 문제 없음.
• FN/FP: '찐'으로 코로나에 걸렸는데, 키트에서 음성으로 뜨는 것. '찐'으로 코로나에 안걸렸는데, 키트에서 양성으로 뜨는 것. -> 문제 있음.

2.1.1 Type I errors

• Type 1: 귀무가설이 실제로는 참인데, 기각하는 것.
  실제 음성(Negative)인 것을 양성(Positive)로 판정
  거짓 양성(False positive) 또는 알파 오류(α error)라고 불림.
  Type 1 error의 0.05%, 5% 유의수준은 귀무가설이 5%의 확률로 '잘못 기각'된다는 의미.
  예) 질병이 없는데, 있다고 뜨는 경우 / 불이 안 났는데, 불이 났다고 경보기가 울리는 경우.
  귀무가설: 질병이 없다. (기각) 대립가설: 질병이 있다 (채택)
  + p-value와의 관계
  p-value는 1종 오류를 범할 확률과 동일하다.
  p-value가 0.05. 즉, 5%라는 말은 100번 중 5번만 1종 오류를 범했다는 의미다.
  95%의 신뢰도로 귀무가설을 기각하고 대립가설을 채택한다는 뜻이다.
  그래서 유의 수준을 0.05, 5%로 정했을 때 p-value의 값이 0.05보다 적게 되면 1종 오류가 일어날 확률이 줄어들게 되고 귀무가설을 기각할 수 있게 되는 것이다.

2.1.2 Type II errors

• Type 2: 귀무가설이 실제로는 거짓인데, 채택하는 것.
  실제 양성(Positive)인 것을 음성(Negative)으로 판정
  거짓 음성(False Negative) 또는 베타 오류(β error)라고 불림.
  예) 질병이 있는데, 질병이 없다고 하는 경우 / 불이 났는데, 화재 경보기가 가만히 있는 경우.
  귀무가설: 질병이 없다. (채택) 대립가설: 질병이 있다.(기각)

• 일반적으로 α와 β의 확률은 서로 trade-off(하나가 커지면, 하나는 줄어든다)관계이다.

• 어쩌다 우연히 발생한 차이에 속지 않도록 하는 것이 목적이라 보통 '1종 오류'를 최소화 하고자 한다.

2.2 Chi-square test

• 교차분석(cross-tabulation analysis)이라고도 부르며 카이제곱 검정이라고도 한다. χ2 (x랑 다름, '카이'라고 부르며 그리스어)

• 범주형 데이터 사이의 상호관련성을 확인하기 위해 교차표(Table)를 만들어 관계를 확인하는 분석 방법이다.

• 관찰 빈도와 기대 빈도의 차이가 유의미한 수준으로 나는지, 아닌지를 검정한다.
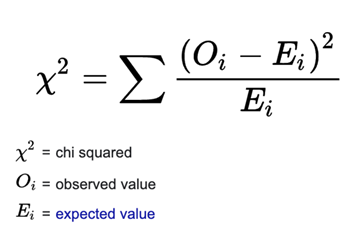  (관측 빈도에서 기대 빈도를 뺀 값)의 제곱을 기대빈도로 나눈 값.

• 이것도 p-value를 활용해서 귀무가설의 기각 여부를 결정한다.
  예) 귀무가설: 가족의 수와 자동차의 크기는 독립적이다(=가족의 수와 자동차의 크기는 연관성이 없다.)
  대립가설: 가족의 수와 자동차의 크기는 독립적이지 않다.(=가족의 수에 따라 자동차의 크기는 다르다.)

+ 범주형 데이터: 'A', 'B', 'C'처럼 종류를 표시하는 데이터. 다른 말로는 카테고리(Category)데이터 라고도 부른다. 예)국적, 혈액형, 거주지 등등
+수치형 데이터(Numerical data): 범주형과 반대되는 개념으로 관측된 값이 숫자로 측정되는 자료를 말한다. 예)시험 성적, 키, 몸무게
++수치형 자료는 다시 키, 몸무게 같은 연속적인 자료와 자동차 사고 건수, 출입횟수 등 셀 수 있는 자료를 말한다. (자동차 사고가 0.4만큼 날 수 없다. 났으면 난거고 안났으면 안난거다.)