[AIB]Note123~4 Confidence interval, Bayesian

1. Confidence interval(신뢰구간)

1.1 ANOVA(ANalysis Of VAriance, 분산분석)

• t-test, chi-square test를 통해 우리는 1개 그룹, 2개 그룹의 값을 살펴 보았다.
  그러면 3개 이상의 그룹을 확인할 수는 없을까?
• 2개 이상의 그룹을 확인하기위해 그룹1 vs 그룹2, 그룹2 vs 그룹3, 그룹1 vs 그룹3을 각각 하면 되지 않을까? 생각할 수 있다. 이론적으로는 가능하지만 문제가 있다.
• 3벌의 가설 검정에서 각각 매번 통계적으로 에러가 발생할 확률은 α이다.
  α = 0.05라면. 3개의 가설 검정 중 적어도 하나에서 에러가 날 확률은 1-(1-α)^3이고 이는 약 15%에 달한다.
• 또 m개 그룹에 대한 가설 검정이라면
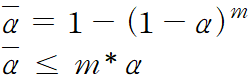  라는 것이 증명되어 있다. 즉, 하나씩 여러번 비교하는 것은 그룹수가 늘어날수록 정확도가 떨어진다는 것!
• 그래서 한번에 3개 이상의 그룹을 비교할 수 있는 ANOVA검정이 나오게 되었다. (정규성, 동분산성, 독립성 만족해야함 / 각 그룹의 평균이 서로 차이가 있는지 밖에 확인해주지 않는다)
• 여러 그룹들이 하나의 분포에서 나왔다는 가정을 통해 검정을 할 수 있다. 이를 위한 지표는 F-statistic. 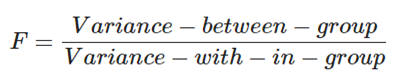표본 그룹 간 분산 / 표본 그룹 내 분산
  F값이 높다는 것이 가지는 의미는

1. 분자(다른 그룹끼리의 분산)는 크고, 분모(전체 그룹의 분산)는 작아야 한다.
2. 다른 그룹끼리의 분포가 다를 것이다. 라는 가정이 붙게 된다.
3. 따라서 F값이 커지는 것은 그룹 사이의 차이가 크다 // F값이 작아지는 것은 그룹 사이의 차이가 적다.

1.2 관련 법칙과 정리들

1.2.1 큰 수의 법칙(Law of large numbers)

• Sample 데이터의 수가 커질수록, sample 통계치는 점점 모집단의 모수와 같아진다.
• Sample이 10, 20, 30,,, 100, 1000개로 커질 수록 모집단과 가까워진다.

1.2.2 중심극한정리(Central Limit Theorem, CLT)

• Sample 데이터의 수가 많아질수록, sample의 '평균'은 정규분포에 근사한 형태로 나타난다.
• Sample 10번 수집하는 것(Sampling)을 10번, 100번, 1000번 할 수록으로 이해하면 될듯...?
• 학교 다닐 때, 학부 수준에서는 통계치를 구할 때 샘플의 갯수를 30개 정도로 하고 이를 뒷받침 하는 근거로 CLT를 사용하면 된다고 배웠었다. 가장 강력한 도구라고....

+ 정규분포(Normal distribution 혹은 가우스 분포, Gaussian distribution)
평균(μ, 뮤)을 중심으로 좌우가 대칭이며 종 모양으로 생긴 분포. 곡선은 확률 밀도 함수. 곡선 아래의 면적 = 확률, 아래 면적 넓이의 합은 '1' (확률은 모두 더하면 1이 나온다.) 이 때 평균이 0, 분산이 1일 때의 분포를 표준 정규 분포라고 한다.

1.3 Confidence interval(신뢰 구간)이 무엇인가?

• 신뢰 구간은 모수가 어느 범위 안에 있는지를 확률적으로 보여주는 방법이다.
• 대한민국 국민의 평균 수명이 얼마일까? 를 생각해 보았을 때
• 점 추정(Point estimate): 평균 100세일 것. 딱 하나의 지점(Point)로 추측하는 방법.
• 구간 추정(Interval estimate): 70~80세일 것. 60~90세 일 것. 0~120세 일 것. Point로 추측하는 것이 아니라 구간으로 추측하는 것.
• 점 추정은 '모'아니면 '도'인데 틀릴 확률이 높을 수밖에 없다.
  70~80세는 차이가 10세 밖에 안나지만 대신에 실제 평균 수명이 70~80세 안에 들어가기가 힘들 수 있다.
  하지만 0~120세는 이 악물고 맞추고자 하는 의지로 볼 수 있겠다. 대신 그렇게 해서 맞추더라도 별 의미는 없다. 마치 물을 마시는 사람은 200년 안에 죽는다와 같은 상식선에서도 해결가능한 문제이기 때문.
• 즉, 예측하는 범위(70~80세 vs 0~120세)와 적당히 맞출 수 있는 수준을 적절하게 설정해주어야한다.

1.4 정규화(Normalization)와 표준화(Standardization)

• 데이터의 단위, 값의 범위 등의 Scale을 맞춰주는 작업임.
• 우리나라 돈 1억 원과 일본 엔화 1억 엔과 미국 1억 달러, 비트코인 1억 코인이 지니고 있는 시장가치가 같다고 하는 사람은 없다. 모두 각자의 시장에서 1억 OO으로 거래가 되지만, 가치는 모두 다르기 때문이다. 그런데 우리나라 경제와 미국 경제를 비교할 때에 하나로 통일 시켜주지 않으면 데이터가 이상하게 나오게 될 것이다. 그렇기에 데이터를 분석하기 이전에 먼저 Scale을 통일시켜 줄 필요가 있는데 이와 비슷한 의미로 이해하면 좋을 것.
• 정규화: 한 특성 내에 가장 큰 값은 1, 가장 작은 값은 0으로 변환시켜 준다.
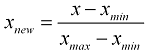
  식: (측정값 - 최소값) / (최대값 - 최소값)
  데이터 집단에서 A라는 데이터가 가지는 위치를 확인할 수 있다.
• 표준화: 데이터를 0을 중심으로 양쪽으로 분포시키는 방법. 이렇게 하면 모든 데이터들은 평균을 기준으로 얼마나 떨어져 있는지를 보여준다.
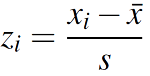
  식: (측정값 - 평균) / 표준 편차
• 뭐가 더 좋아요? : Case by Case 절대적인 방법은 없고 상황에 맞게 조율해주는 것이 필수!

2. Bayesian(베이지안 추론)

• 베이지안 정리, 추론, 통계 등등의 핵심은 기존의 데이터에서 '새로운 사건'을 추가함으로써 예측의 정확성을 높여주는 것이다.
• https://youtu.be/Y4ecU7NkiEI 2월 14일은 발렌타인데이인데 내가 초콜렛을 받았다? 그럼 나에게 호감을 갖고 있을까 아닐까? 를 베이지안 추론을 사용해서 확인해본다.
• https://youtu.be/eMA9KjDQBsA 3개의 문 중에서 2개는 염소, 1개는 GV80이 있다. 내가 문 하나를 선택하고 그 문에 GV80이 있으면 GV80 겟또~☆ 하지만 염소가 있으면 망.... 그럴때 어떤 선택을 하는 것이 GV80을 얻을 확률을 높여줄까?
  
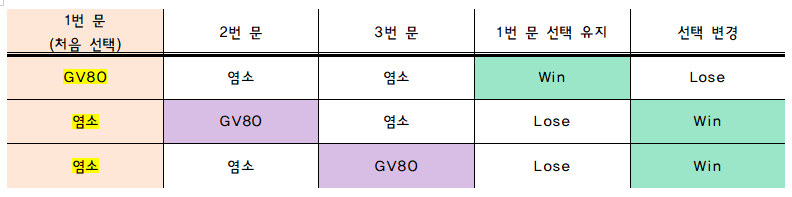
• 처음 선택했을 때에는 1/3의 확률로 GV80이 있다.
  그리고 사회자가 내가 선택하지 않은 문 중에 염소가 있는 문을 열어준다.
• 이 때 내가 다시 선택을 하면 GV80을 고를 확률이 2/3으로 두 배가 된다! 2배 이벤트
• 이게 베이지안 추론의 핵심! 정보가 새로 추가되고 확률이 올라간다는 것!!

2.1 조건부 확률(The Law of Conditional Probability)

• B가 일어났을 때 A가 일어날 확률
  
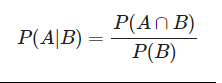
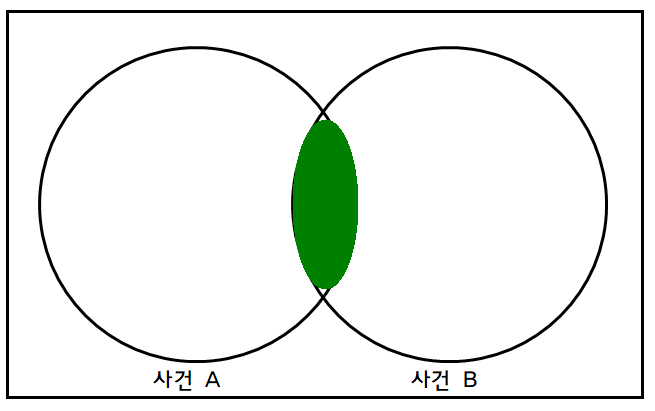
• 전체 사각형이 모든 가능한 확률 공간, A와 B의 교집합이 가운데 색칠된 부분.

2.2 베이지안 이론(Bayes Theorem)

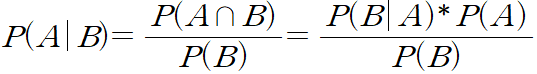
• 사전 확률. B라는 정보가 업데이트 되기 전의 확률
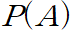
• 사후 확률. B라는 정보가 업데이트 된 후의 확률
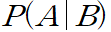
• 일종의 Data이자 확률을 업데이트 할 수 있는 증거, 정보.
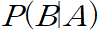
• 베이지안 테스트를 반복하여 사용하면 그 정확성이 업데이트 된다. 데이터를 업데이트 해서 예측의 정확성을 높이기 위해 사용한다.