
1. Dimension reduction(차원 축소)
1.1 Vector transformation(벡터 변환)
- https://youtu.be/g-Hb26agBFg
- 선형 변환은 임의의 두 벡터를 더하거나 스칼라 곱을 하는 것을 말한다. 두 벡터 공간 사이의 함수, 한 점을 한 벡터 공간에서 다른 벡터 공간으로 이동시키는데 그 이동규칙을 선형 변환이라고 한다.
- f를 활용해서 임의의 두 벡터[x1, x2])에 대해서 [2x1+x2, x1-3x2]로 변환할 수 있다.
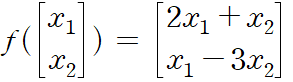
- 그렇기에 위의 f를 활용하는 것은 T를 곱해주는 것으로 이해할 수 있다.
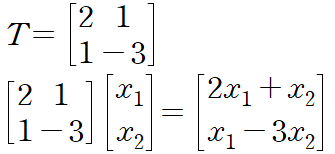
- 임의의 벡터를 다른 벡터로 변환하는 과정은 특정 T 매트릭스를 곱하는 것과 동일하다.
1.2 Eigenvector(고유벡터)
- Transformation은 Matrix를 곱해 벡터(=데이터)를 다른 위치로 옮긴다는 뜻.
- 행렬 A를 선형 변환으로 위치를 옮겨 새롭게 볼 때에 선형 변환 A에 의한 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터
- 벡터를 변환할 때, 크기만 변화하고 방향은 변하지 않는 벡터
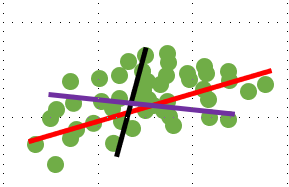
- 위의 그림에서 빨강, 보라, 검정 세 가지 선 중에서 초록색 데이터를 (그나마) 가장 잘 표현할 수 있는 선은 바로 빨간 선이다. 빨간 선을 저 초록 데이터의 고유 벡터로 이해하면 좋다.분산이 큰 vector를 선택해주어야 한다.
(이렇게 이해함...)
1.3 Eigenvalue(고유값)
- 고유벡터에서 상수배의 값.
- 변화한 크기의 값.
- 고유벡터와 고유값은 항상 쌍을 이루고 있다.
1.4 PCA(Principle Component Analysis, 데이터 차원 축소)
1.4.1 PCA는 뭘까?
- 주성분 분석이라고도 한다. 기존의 여러 변수를 재조합(Selection, Extraction)하여 고차원에서 저차원으로 차원을 축소해준다.
1.4.2 PCA를 해야하는 이유.
- 첫째: 1차원은 선(x축), 2차원은 면(x, y축), 3차원은 입체(x, y, z축)으로 표현할 수 있다. 그리고 우리가 이해할 수 있다. 그렇지만 4차원, 6차원, 10차원은??? 이해할 수 없다.
- 둘째: 데이터를 분석할 때 사용하는 feature가 모두 똑같은 비중으로 중요하지가 않다.
예를 들어 우리나라 경제를 분석할 때 여러 중요한 것 중에 하나는 수출입이다. 우리나라가 교역하는 국가 중에서 미국, 중국, 일본의 중요도와 남아프리카공화국, 적도기니, 팔라우와 같은 국가들이 분석에 차지하는 비중은 크게 차이날 수 밖에 없다. 그렇기에 전자의 경우는 한국의 경제 분석에 꼭 포함시켜야 하지만, 후자의 국가들은 제외하고 분석하여도 그 결과에 큰 차이가 나지 않을 것이다.
데이터를 분석할 때에도 이와 비슷한 이유로 중요한 feature는 포함시키고 나머지는 제외시키는 것이 중요하단 뜻! - 셋째: Overfitting(과적합)의 문제, 샘플(데이터)의 수에 비해 feature의 수가 너무 많은 경우 과적합의 문제가 발생한다. 과적합은 주어진 샘플은 너무나도 잘 설명하지만, 주어진 샘플을 제외하고 실제 데이터에서는 힘을 제대로 못 쓰는 경우를 의미한다.
아래의 그림과 같은 경우라고 이해하면 된다. 보라색은 분석에 사용한 데이터, 주황색은 새로운 실제 데이터. 회귀 분석을 진행하였을 때 주황색, 실제 데이터에도 적합해야 하지만 초록색 선은 전혀 반영하지 못하고 있다.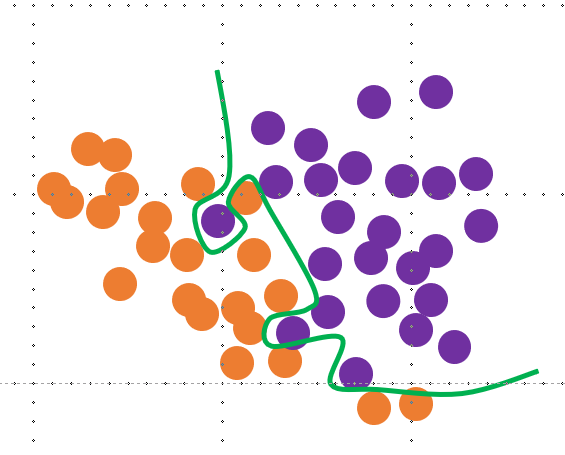
1.4.3 PCA는 어떻게 할까?
- 차원 축소에는 여러 방법이 있는데 여기서는 크게 Selection과 Extraction을 살펴본다.
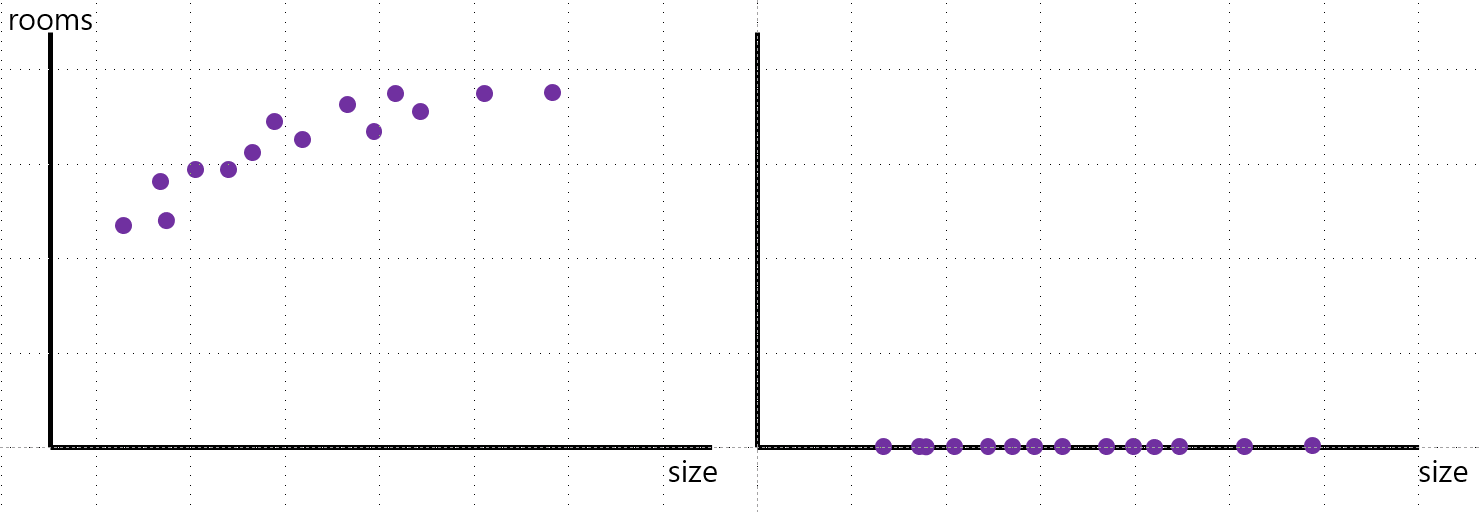
- Selection(선택): 왼쪽의 데이터는 x축에 size, y축에 rooms를 두어 2차원으로 표현했다. 하지만 오른쪽의 그래프는 x축 size만 남겨두어 1차원으로 축소했다. 이런 것이 pca, 데이터 차원 축소의 일종이다.
장점: 선택한 feature를 해석하기 쉽다.
단점: 선택하고 선택하지 않은 feature 사이의 연관성을 염두해두어야 한다.
예) LASSO, Genetic algorithm 등 - Extraction(추출): 기존에 있는 feature와 그것을 활용해 새롭게 만든 feature를 사용하는 것. 마치 커피의 원두를 로스팅 하는 것과 비슷하다.
장점: feature 사이의 연관성이 고려된다. feature 수를 많이 줄일 수 있다.
단점: 그렇게 해서 나온 feature의 해석이 어렵다.
예) PCA, Auto-encoder 등
+ 벡터를 바꾼다: 벡터의 방향을 바꾸거나(덧셈), 크기를 바꾸거나(곱셈)
2. Clustering
2.1 Scree plots
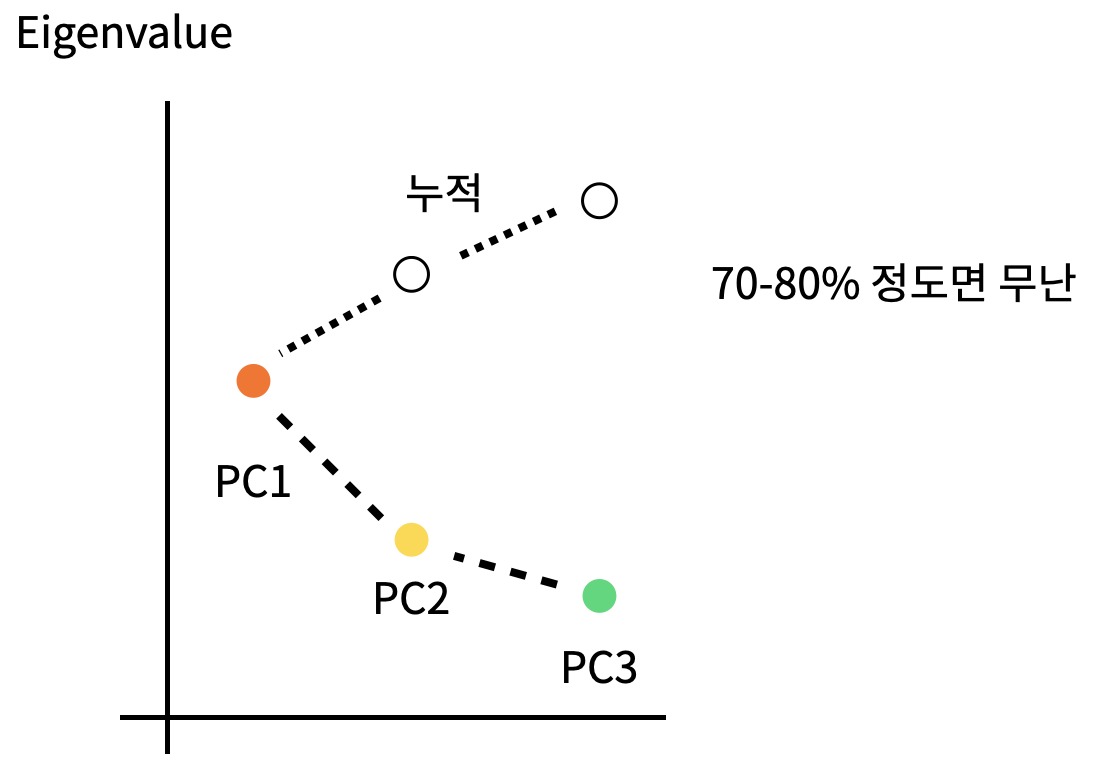
- pca를 통해 차원을 축소한다고 했다. 그러면 축소를 하는데 얼마나 축소해야하나? 가 문제가 될 수 있다.
- scree plot은 주성분을 x축에, 주성분의 Eigenvalue(고유값, 분산)을 y축에 두고 시각적으로 얼마나를 판단하게 도와준다.
2.2 지도학습과 비지도학습
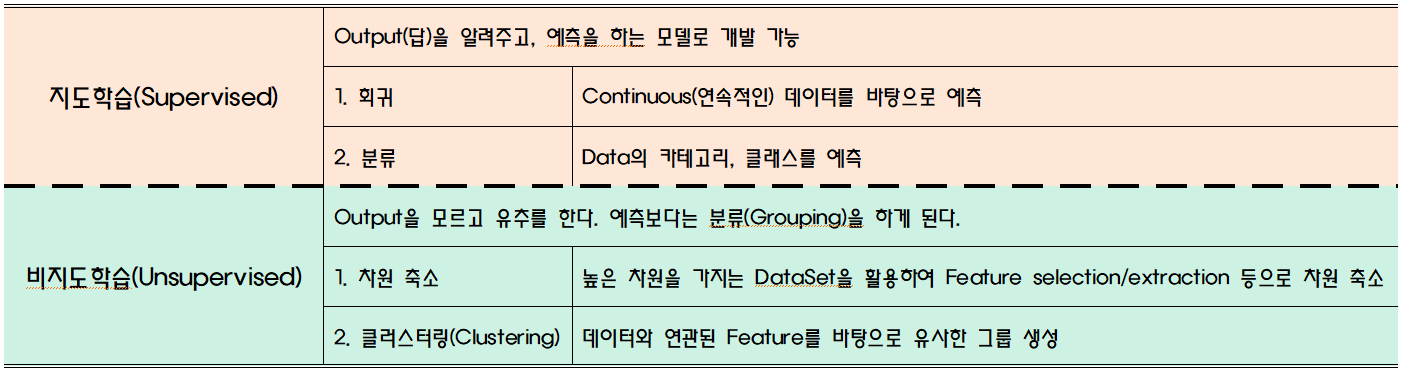
- 강화학습(Reinforcement): 머신러닝의 여러 유형 중 하나. 기계가 좋은 행동을 할 경우 보상, 그렇지 않을 경우 처벌
(그렇다고해서 몽둥이로 컴퓨터를 때리지는 않는다....)
2.3 Clustering(클러스터링)
- Unsupervised Learning의 한 종류
- 주어진 데이터들이 얼마나 그리고 어떻게 유사한지 알 수 있다.
- 하지만 정답을 보장하지 않기에 EDA를 위한 방법으로 많이 사용된다.
- 다만, 우리가 알 수 없는(혹은 몰랐던) 특성을 찾아내준다.
2.3.1 Hierarchical(계층, 위계)
- Aggolomerative(병합): 개별 포인트에서 시작 후 점점 크게(위로) 합쳐간다.
- Divisive(구분): 한개의 큰 클러스터에서 시작해서 점점 작게(아래로) 나뉘어져 간다.
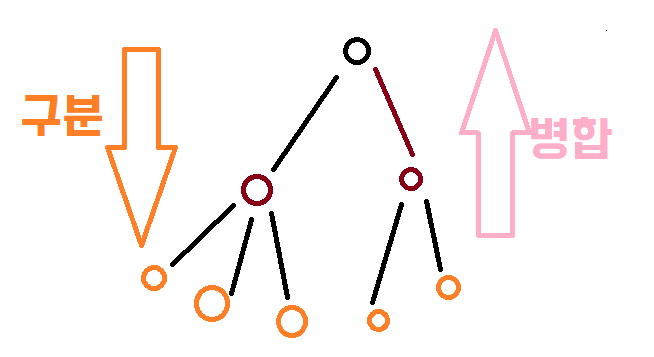 (이미지를 어떻게 표현해야하나 고민하다... 그림판으로 했습니다... ㅜㅜ)
(이미지를 어떻게 표현해야하나 고민하다... 그림판으로 했습니다... ㅜㅜ)
2.3.2 K-means Clustering
- https://www.naftaliharris.com/blog/visualizing-k-means-clustering/ 실습해볼 수 있는 사이트
- 임의로 spot을 만들고 가장 가까운 것으로 Grouping 및 spot은 각각의 그룹의 중앙으로 이동한다.
- 과정: 1) k개의 랜덤한 데이터를 cluster의 중심점으로 설정. 2) 중심점 근처(가장 가까운 데이터)의 데이터를 해당 cluster로 할당한다. 3) 변경된 cluster에 대해 중심점을 새로 계산. 4)cluster에 유의미한 변화가 없을 때까지 2)~3)을 계속 반복
- K를 결정하는 방법: 1)They Eyeball Method: 사람이 주관적으로 K를 판단 2)Metrics: 객관적인 지표를 설정하여 K를 결정
- Elbow Method: k의 개수가 3일때 최적. L자 모양의 그래프가 사람의 팔꿈치와 닮았다고 해서 Elbow라고 부른다. 팔꿈치 모양의 k를 선택하면 된다.
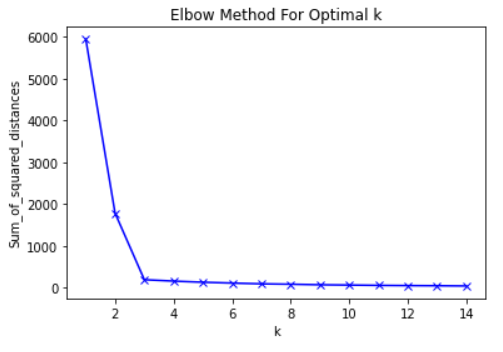
+ K의 개수에 따라 달라지는 그룹
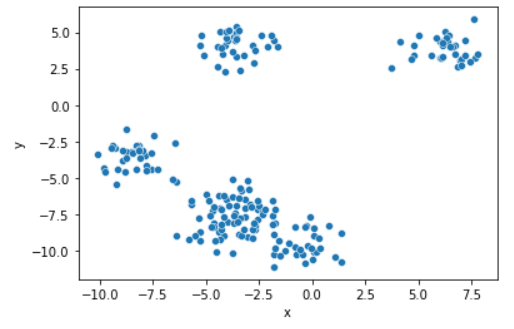 원본 scatter plot
원본 scatter plot
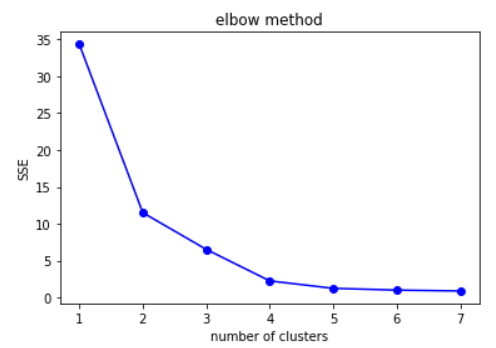 위 그래프를 보았을 때에는 4개가 좋아보인다.
위 그래프를 보았을 때에는 4개가 좋아보인다.
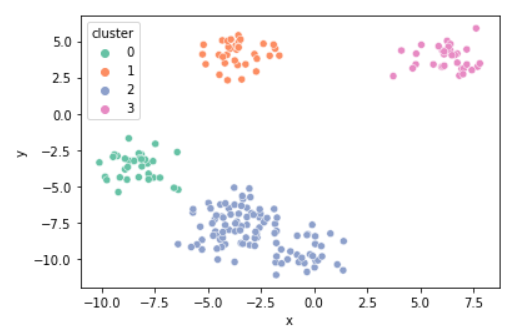 k = 4
k = 4
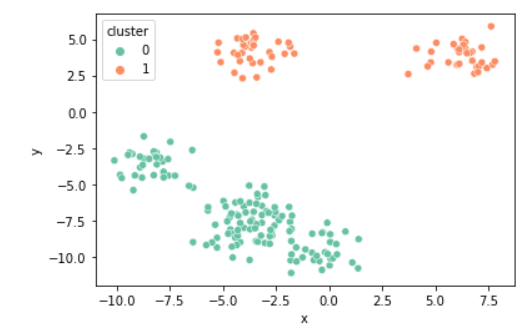 k = 2
k = 2
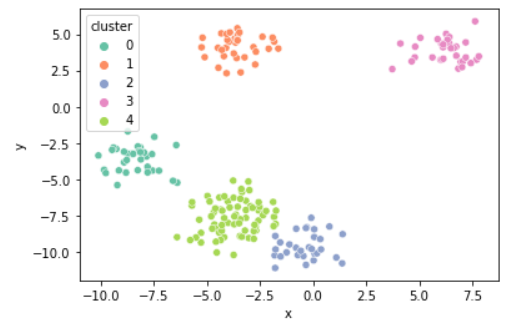 k = 5
k = 5
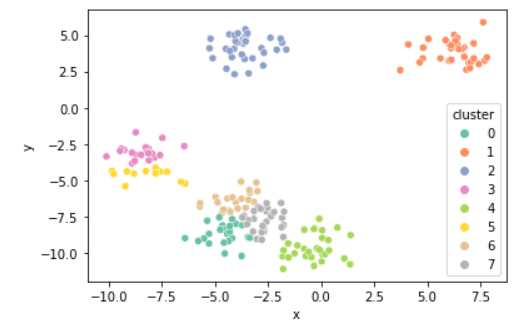 k = 8
k = 8
