
📚 K-최근접 이웃 알고리즘 (K-NN)
KNN 알고리즘은 상당히 간단한 모델이고, sklearn으로 쉽게 구현 가능한 모델이다. 우리는 데이터 전처리 과정 중 KNN 알고리즘을 이용하여 다양한 결측치, 이상치 등의 값을 대체할 수 있다.
먼저, 아래 그림과 함꼐 보자.
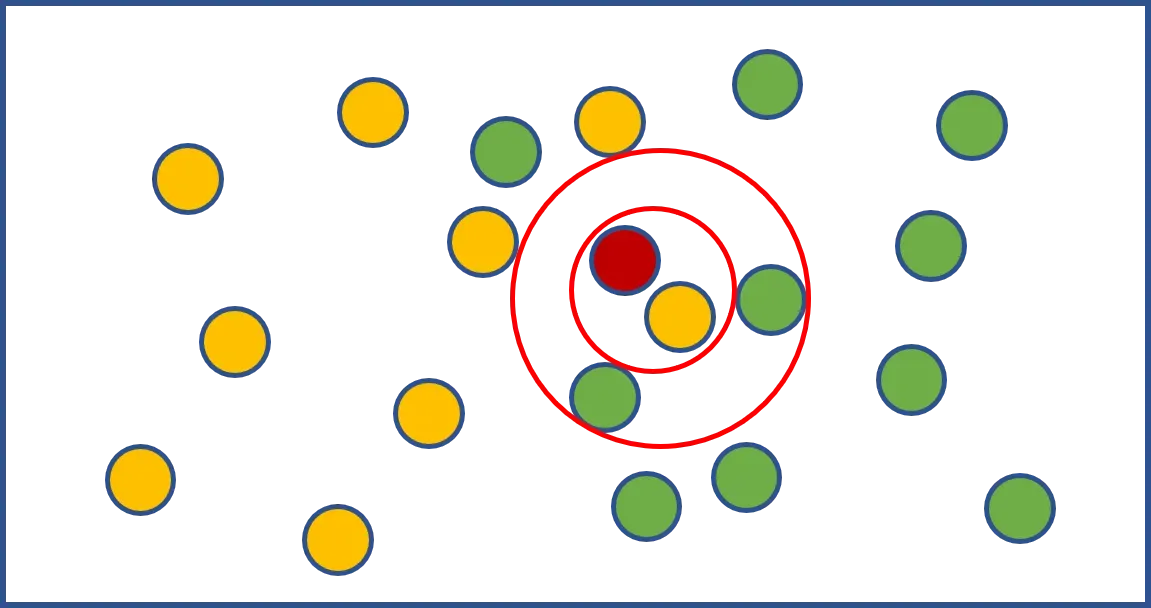
KNN은 위의 그림의 빨간색 원처럼 새로운 데이터가 주어졌을 때 기존 데이터 가운데 가장 가까운 K개 이웃의 정보로 새로운 데이터를 예측하는 방법이다.
분류모델인 경우 위의 그림에서 만약 K가 1이면 주황색으로 분류하는 것이고 K가 3이면 녹색으로 분류하는 것이다. 만약 Linear Regression 문제라면 이웃들의 종속변수의 평균이 예측값으로 결정된다.
위의 설명에서 알 수 있듯이 KNN은 딱히 학습이라고 부를 수 있는 절차가 없다.
새로운 데이터가 들어왔을 때 기존 데이터들과의 거리를 계산하여 이웃들을 뽑아서 예측을 수행하기 때문이다.
때문에 Instance-based Learning 혹은 Lazy Model이라고 부르기도 한다.
Regression처럼 데이터로부터 모델을 생성한 후 예측을 진행하는 Model_based Learning과 대비되는 개념이고, 별도의 모델 생성과정 없이 관측치(distance)만을 이용하여 분류와 회귀작업을 수행한다.
KNN의 hyperparameter는 2가지이다.
탐색할 이웃 수인 K, 그리고 거리 측정 방식이다.
K가 작을 경우 지역적 특성을 지나치게 반영하는 overfitting이 발생할 수 있으며 K가 너무 크면 과하게 정규화되는 경향인 underfitting이 될 수 있다. 또한 KNN을 수행하기 전 정규화 작업을 반드시 수행해야 한다.
📚 KNN의 장점
-
KNN 알고리즘은 학습데이터에 포함되어 있는 noise에 크게 영향을 받지 않으며 학습 데이터의 수가 많다면 꽤 효과적인 알고리즘으로 알려져 있다. 특히 Mahalanobis 거리와 같이 데이터의 분산을 고려할 경우 꽤 robust한 방법론으로 알려져 있고 현업에서도 많이 사용되는 방법이다.
-
K값이 1인 1-NN의 오차범위는 가장 이상적인 오차범위의 2배보다 같거나 작다는 것이 수학적으로 증명되어 있다. 쉽게 말하면 1-NN에 한해서는 어느정도 모델 성능보장을 할 수 있다는 의미이다.
📚 KNN의 단점
Hyperparameter인 K의 개수와 어떤 거리척도가 분석에 적합한지 대한 내용이 불분명하다. 따라서 임의로 선택해야 하는 단점도 가지고 있고, 새로운 관측치와 각각의 학습데이터 사이의 거리를 전부 계산해야 하는 문제가 있기 때문에 시간이 오래 걸린다는 단점이 있다.
📚 KNN 구현
이제 KNN을 코드로 구현하고 K 값에 따른 결과도 비교해보자. 데이터 셋은 Ozone Data Set을 사용할 것이다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.preprocessing import MinMaxScaler
from sklearn import linear_model
from sklearn.neighbors import KNeighborsRegressor📚 Raw Data Loading
ozone = pd.read_csv('/파일경로/ozone.csv')
df = ozone[['Solar.R', 'Wind', 'Temp', 'Ozone']]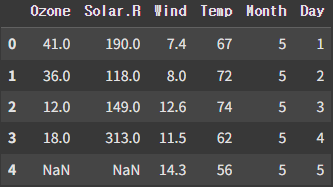
📚 데이터 전처리
# 결측치 처리 (지금은 삭제 처리)
new_df = df.dropna(how='any', inplace=False)
# 이상치 처리 (지금은 삭제 처리)
zscore_threshold = 1.8
mask = np.abs(stats.zscore(new_df['Ozone'])) <= zscore_threshold
df1 = new_df.loc[mask]
# 데이터 정규화
# 데이터 분리
x_data = df1.drop('Ozone', axis=1, inplace=False).values
t_data = df1['Ozone'].values.reshape(-1, 1)
scaler_x = MinMaxScaler()
scaler_t = MinMaxScaler()
scaler_x.fit(x_data)
scaler_t.fit(t_data)
x_data_norm = scaler_x.transform(x_data)
t_data_norm = scaler_t.transform(t_data)결측치, 이상치는 간단하게 삭제 처리를 하였고, KNN 알고리즘 사용을 위해 정규화 작업을 진행하였다.
📚 Test Data 준비
test_data = np.array([[310, 15, 80]])Solar.R = 310, Wind = 15, Temp = 80 에 대해 예측을 진행할 것이다.
📚 KNN Model 구현 및 예측
knn_regressor = KNeighborsRegressor(n_neighbors=2)
knn_regressor.fit(x_data_norm, t_data_norm)
test_data_norm = scaler_x.transform(test_data)
result_knn_norm = knn_regressor_2.predict(test_data_norm)
result_knn = scaler_t.inverse_transform(result_knn_2_norm)
print(result_knn) # [[33.]]우선 K를 2로 지정하였을 때 33이라는 결과를 예측하였고, 정규화된 데이터로 학습을 진행하였기 때문에 test data 역시 정규화하여 예측을 진행하여야 한다.
📚 n_neighbors에 따른 결과 변화
neighbors = []
result = []
for i in range(1, 11):
knn_regressor = KNeighborsRegressor(n_neighbors=i)
neighbors.append(i)
knn_regressor.fit(x_data_norm, t_data_norm)
test_data_norm = scaler_x.transform(test_data)
result_knn_norm = knn_regressor.predict(test_data_norm)
result_knn = scaler_t.inverse_transform(result_knn_norm)
result.append(result_knn.ravel())
plt.plot(neighbors, result)
plt.xlabel('result')
plt.ylabel('n_neighbors')
plt.show()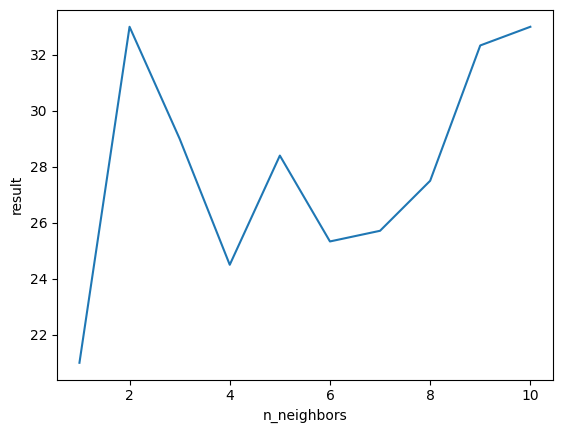
K값을 1 ~ 10까지 변경해 가면서 예측한 result의 변화를 나타낸 그래프이다. 이처럼 KNN의 경우 K값에 따라 결과가 달라질 수 있으니 사용할 땐 이러한 점을 주의해야 한다.
