[Machine Learning] 다중 선형 회귀 - Multiple Linear Regression

---

📚 Multiple Linear Regression

Multiple Linear Regression
독립변수가 1개가 아닌 여러개인 선형 회귀 모델

Multiple Linear Regression의 경우 단지 독립변수가 여러개 결합되어 있다는 것, 이에 따라 구해야할 Weight 역시 여러개라는 것 이외에는 Simple Linear Regression 구현과 크게 다르지 않다.

이번엔 저번 글에서 다룬 KNN을 이용하여 데이터 전처리 후, sklearn과 tensorflow를 사용하여 Multiple Linear Regression을 구현해보자.

import numpy as np
import pandas as pd

from scipy import stats
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import MinMaxScaler

from sklearn.linear_model import LinearRegression

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten, Dense
from tensorflow.keras.optimizers import SGD

---

📚 Data Preprocessing

다음과 같은 방식으로 데이터 전처리 후, 학습을 진행할 것이다.

1. 독립변수에 대한 결측치는 median으로 처리
2. 독립변수에 대한 이상치는 mean으로 처리
3. 종속변수에 대한 이상치는 검출한 후 mean으로 처리
4. 데이터 정규화
5. 종속변수에 대한 결측치는 KNN을 이용하여 예측값으로 처리

---

📚 Raw Data Loading

df = pd.read_csv('/content/drive/MyDrive/KDT/data/ozone.csv')
training_data = df

x_data = training_data[['Solar.R','Wind','Temp']]
t_data = training_data['Ozone']

display(x_data.head())
display(t_data.head())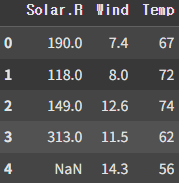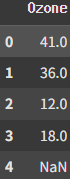

---

📚 독립변수에 대한 결측치 처리

for col in x_data.columns:
    col_median = np.nanmedian(x_data[col])
    x_data[col].loc[x_data[col].isnull()] = col_median

먼저 독립변수에 대한 결측치를 검출한 후, median 값으로 처리하였다. 이때 아직 이상치에 대해 처리되지 않았음으로 mean 값으로 처리하지 않았다.

---

📚 독립변수에 대한 이상치 처리

zscore_threshold = 1.8

for col in x_data.columns:
    outliers = x_data[col][(np.abs(stats.zscore(x_data[col])) > zscore_threshold)]
    col_mean = np.mean(x_data.loc[~x_data[col].isin(outliers), col])
    x_data.loc[x_data[col].isin(outliers), col] = col_mean
    print(col_mean)
    # 198.6013986013986 <- Solar.R column
	# 9.820279720279721 <- Wind column
	# 78.75524475524476 <- Temp column

이후 독립변수에 대한 이상치를 Z-Score를 사용하여 검출 후, mean 값으로 처리하였다.

---

📚 종속변수에 대한 이상치 처리

outliers = t_data[(np.abs(stats.zscore(t_data)) > zscore_threshold)]
col_mean = np.mean(t_data[~t_data.isin(outliers)])
t_data[t_data.isin(outliers)] = col_mean
print(col_mean)
# 42.12931034482759 <- Ozone column

확인결과 종속변수에 대한 이상치는 없었지만 존재하는 경우 위와 같이 처리할 수 있다.

---

📚 데이터 정규화

scaler_x = MinMaxScaler()  # MinMaxScaler 클래스의 인스턴스 생성.
scaler_t = MinMaxScaler()  # MinMaxScaler 클래스의 인스턴스 생성.

scaler_x.fit(x_data.values)
scaler_t.fit(t_data.values.reshape(-1,1))

x_data_norm = scaler_x.transform(x_data.values)
t_data_norm = scaler_t.transform(t_data.values.reshape(-1,1)).ravel()

KNN, Tensorflow 모델에 데이터를 사용하기 위해 데이터 전처리를 해주어야 한다.

---

📚 종속변수에 대한 결측치 처리 (KNN)

x_data_train_norm = x_data_norm[~np.isnan(t_data_norm)]
t_data_train_norm = t_data_norm[~np.isnan(t_data_norm)]

knn_regressor = KNeighborsRegressor(n_neighbors=2)
knn_regressor.fit(x_data_train_norm, t_data_train_norm)


knn_predict = knn_regressor.predict(x_data_norm[np.isnan(t_data_norm)])
t_data_norm[np.isnan(t_data_norm)] = knn_predict
print(knn_predict)
# [0.08383234 0.18562874 0.07784431 0.19161677 0.26946108 0.28143713
#  0.17664671 0.13173653 0.26047904 0.53592814 0.19161677 0.32634731
#  0.61377246 0.61377246 0.19760479 0.19760479 0.11676647 0.07784431
#  0.28742515 0.21556886 0.11676647 0.11676647 0.08083832 0.07784431
#  0.04191617 0.1497006  0.23652695 0.1497006  0.32335329 0.67365269
#  0.19760479 0.67664671 0.23353293 0.11377246 0.08682635 0.51796407
#  0.08682635]

다음과 같이 위에서 처리한 데이터를 통해 종속변수에 대한 결측치를 KNN 모델을 통해 예측하여 Multiple Linear Regression 모델 학습에 사용할 수 있다.

이제 모든 데이터 전처리 작업이 끝났으니 Multiple Linear Regression 모델을 구현해보자.
예측할 데이터는 다음과 같다.

test_data = [[310,15,80]] # Solar>r, Wind, Temp

---

📚 Multiple Linear Regression 구현 (sklearn)

model = LinearRegression()
model.fit(x_data_norm,t_data_norm)
result = model.predict(scaler_x.transform(test_data))

print('sklearn result : {}'.format(scaler_t.inverse_transform(result.reshape(-1,1))))

# sklearn result : [[38.75927452]]

---

📚 Multiple Linear Regression 구현 (tensorflow)

keras_model = Sequential()

keras_model.add(Flatten(input_shape=(3,)))
keras_model.add(Dense(1, activation='linear'))

keras_model.compile(optimizer=SGD(learning_rate=1e-2), loss='mse')

keras_model.fit(x_data_norm,
                t_data_norm,
                epochs=5000,
                verbose=0)

keras_result = keras_model.predict(scaler_x.transform(test_data))

print('tensorflow result : {}'.format(scaler_t.inverse_transform(keras_result.reshape(-1,1))))

# tensorflow result : [[38.64248]]

sklearn, tensorflow 둘 다 Simple Linear Regression과 모델을 구현하는 방식에는 큰 차이가 없는 것을 볼 수 있다.

---