모델(Model): ExponentialSmoothing

calico·2025년 11월 27일

Artificial Intelligence

목록 보기

126/143

1. ExponentialSmoothing(지수평활법)

https://wikidocs.net/266270

statsmodels.tsa.holtwinters.ExponentialSmoothing은 시계열 예측을 위한 고전적이면서도 실무적 활용도가 높은 지수평활법 모델입니다.

추세(Trend), 계절성(Seasonality)을 함께 다룰 수 있어 단기 예측에 특히 강합니다.

ARIMA 계열 대비 설정이 단순하고 빠른 예측 모델이 필요할 때
데이터 패턴이 추세 + 계절성을 명확히 가지고 있을 때
복잡한 ML 모델 대신 해석 가능하고 가벼운 모델이 필요한 프로젝트
전력수요, 매출, 재고소진량 등 주기성 높은 실무 데이터에 적합

2. 모델 종류

단일 지수 평활법(Simple Exponential Smoothing) 은 시계열 데이터에서 추세나 계절성이 없을 때 사용하는 가장 기본적인 예측 기법으로, 최근 데이터일수록 더 큰 가중치를 주기 위해 평활상수 α(0 < α < 1)를 적용해 예측을 업데이트한다. 예측 공식은 다음과 같다.

F_{t+1} = α X_t + (1−α) F_t

여기서 X_t는 실제 관측값, F_t는 예측값이며, α가 클수록 최신 데이터에 민감하게 반응한다. 이 모델은 변화가 크지 않고 비교적 안정적인 시계열에서 효과적이다.

반면 홀트-윈터스(Holt-Winters) 방법은 단일 지수 평활법을 확장해 추세(Trend) 와 계절성(Seasonality) 을 동시에 반영하도록 만든 방식으로, 세 가지 버전이 있다:

Additive 모델: 계절 효과가 일정한 크기일 때(예: 계절적 변동이 ± 일정폭).
Multiplicative 모델: 계절 효과가 데이터 규모에 비례해 커질 때(예: 판매량 증가와 함께 계절성도 커짐).
Triple Exponential Smoothing: 트렌드 + 계절성을 모두 포함하는 완전한 형태로, 현업에서 일반적으로 말하는 “홀트-윈터스 예측”이 이 방식이다.

즉, 추세나 계절성이 없으면 단일 지수 평활법, 추세만 있으면 Holt(이중 지수 평활법), 추세 + 계절성 모두 있으면 Holt-Winters(삼중 지수 평활법) 을 선택하는 것이 표준이다.

1) 단순 지수평활(Simple)

추세/계절성이 없는 데이터에서 사용
가장 기본적인 형태

2) Holt’s Linear (이중 지수평활)

추세(trend) 있는 시계열에 적합
추세 옵션
- add: 선형 증가/감소
- mul: 지수적 증가/감소
- damped: 추세가 시간이 지나며 약해지는 형태

3) Holt-Winters (삼중 지수평활)

추세 + 계절성(seasonality) 데이터를 다룸
계절성 옵션
- add: additive seasonality
- mul: 풍성/빈곤 비율이 변하는 multiplicative seasonality

3. 주요 파라미터 정리

`trend`

None, 'add', 'mul', 'additive', 'multiplicative'
추세 있는 데이터는 add, 증가폭이 커지는 데이터는 mul

`seasonal`

None, 'add', 'mul'
주기적 패턴이 명확하면 설정
multiplicative는 패턴 크기가 비례적으로 변할 때 사용

`seasonal_periods`

계절 주기 길이
- 예: 월별 매출의 연간 주기 → 12
- 일별 시계열의 주간 주기 → 7

`damped_trend`

추세가 시간이 지나면서 약해진다면 True
안정적 예측을 위해 실무에서 자주 사용됨

`use_boxcox`

변동성이 커서 안정화를 원할 때 사용
True, False, 'log', 또는 λ값 가능

`optimized`

True 권장
자동으로 smoothing parameter를 최적화

4. 장점

설정이 단순하면서도 추세 + 계절성을 모두 반영
계산량이 적어 매우 빠름
하이퍼파라미터 튜닝 부담이 적음
실무에서 단기 예측 정확도가 높고 해석 용이

5. 단점

장기 예측에는 부정확
비정상성, 외부 요인 영향이 큰 데이터에서는 한계
갑작스러운 변동(프로모션, 이상치)에 취약

6. 코드 예시 (Python)

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(
    data,
    trend='add',
    seasonal='mul',
    seasonal_periods=12,
    damped_trend=True
).fit()

forecast = model.forecast(12)  # 향후 12개월 예측

단일 지수 평활법 예제


import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing

#예시 데이터 (랜덤 데이터 시계열 생성)
np.random.seed(0)
data = np.random.randn(100)

#pandas의 Series로 변환
time_series = pd.Series(data)

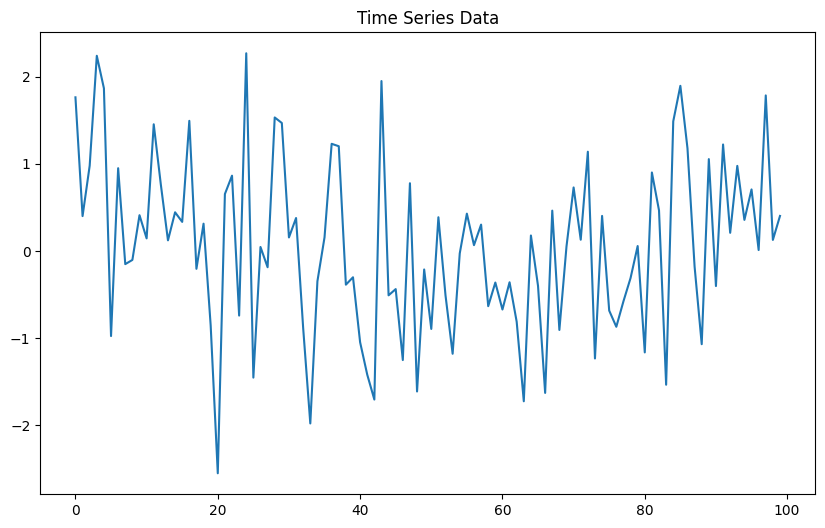
#시계열 데이터 시각화
plt.figure(figsize=(10, 6))
plt.plot(time_series)
plt.title("Time Series Data")
plt.show()

#단일 지수 평활법 (alpha=0.3)
model = ExponentialSmoothing(time_series, trend=None, seasonal=None)
# alpha = smoothing_level
model_fit = model.fit(smoothing_level=0.3, optimized=False)

#예측
forecast_steps = 10
forecast = model_fit.forecast(steps=forecast_steps)

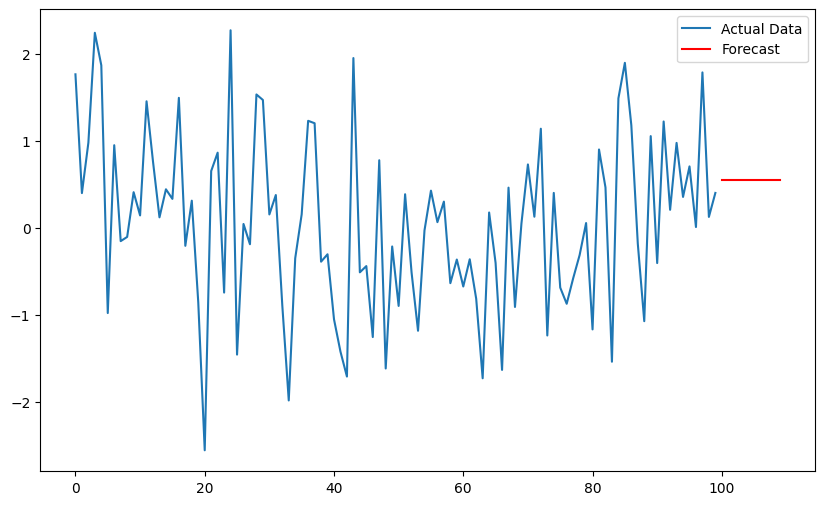
#예측 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(time_series, label="Actual Data")
plt.plot(np.arange(len(time_series), len(time_series) + forecast_steps), forecast, label="Forecast", color='red')
plt.legend()
plt.show()

홀트-윈터스 예제


# 홀트 -윈터스 방법 (Additive Seasonality)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing

#예시 데이터 (랜덤 데이터 시계열 생성)
np.random.seed(0)
data = np.random.randn(100)

#pandas의 Series로 변환
time_series = pd.Series(data)

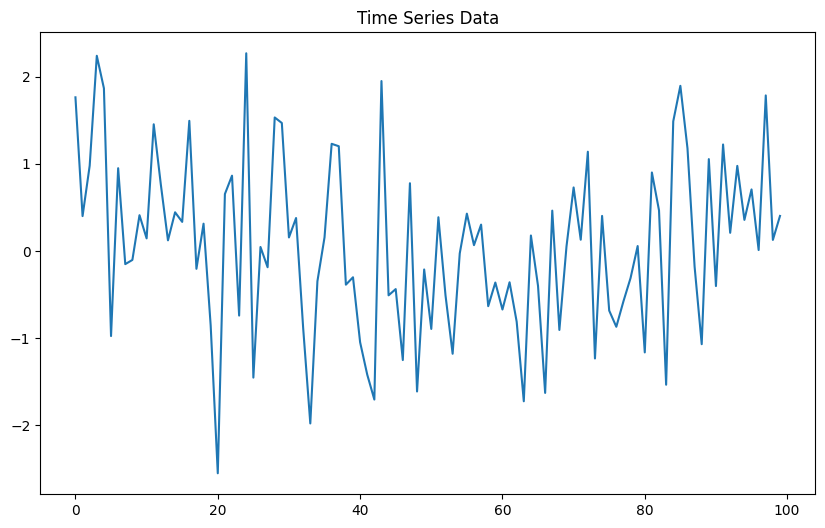
#시계열 데이터 시각화
plt.figure(figsize=(10, 6))
plt.plot(time_series)
plt.title("Time Series Data")
plt.show()

model_hw = ExponentialSmoothing(time_series, trend='add', seasonal='add', seasonal_periods=12)
model_hw_fit = model_hw.fit()

#예측
forecast_hw = model_hw_fit.forecast(steps=12)

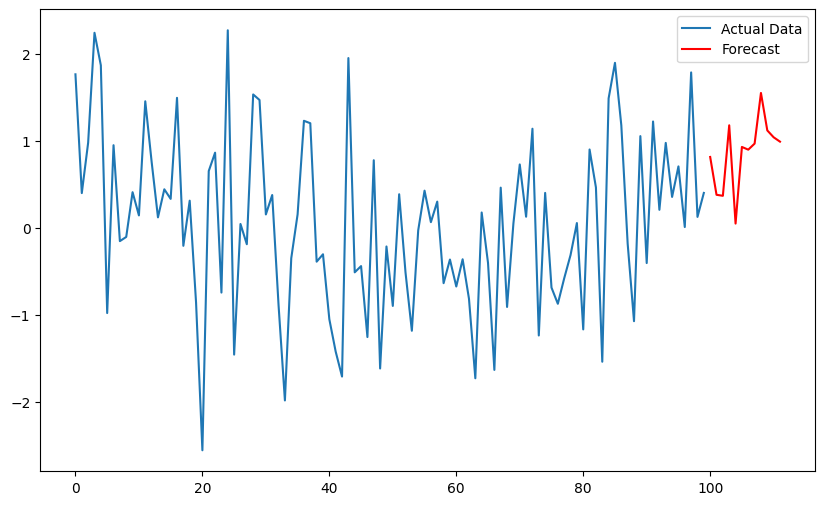
#예측 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(time_series, label="Actual Data")
plt.plot(np.arange(len(time_series), len(time_series) + 12), forecast_hw, label="Forecast", color='red')
plt.legend()
plt.show()