스미스-워터맨(Smith-Waterman) 알고리즘: DPX(Dynamic Programming eXtensions) 명령어

https://mobuk.tistory.com/90

스미스–워터맨(Smith–Waterman) 알고리즘

• 두 서열(sequence)의 지역적 유사성(local similarity) 을 찾기 위한 지역 서열 정렬(Local Sequence Alignment) 알고리즘

  • 생물정보학에서 DNA, RNA, 단백질 서열 비교에 자주 사용되며, Needleman–Wunsch 알고리즘(전역 정렬)과 대조되는 개념입니다.

• 목표: 두 서열의 가장 유사한 부분 구간(subsequence) 을 찾는다.

• 핵심 차이점

  • Needleman–Wunsch: 전체 서열을 처음부터 끝까지 정렬 (Global Alignment)

  • Smith–Waterman: 서열의 일부 구간만 최적 정렬 (Local Alignment)

• 즉, 전체 길이가 아니라 부분적으로 가장 닮은 영역을 찾는 데 집중합니다.

2. 점수 체계 (Scoring Scheme)

• 보통 다음과 같은 점수를 설정합니다.

MATCH     = +1  (같은 문자일 때)
MISMATCH  = -1  (다를 때)
GAP       = -2  (공백 삽입 시)

이 점수는 문제나 데이터에 따라 달라질 수 있습니다.

3. 알고리즘 단계

1) DP 테이블 초기화

• 길이가 각각 m, n인 두 서열 A, B가 있다고 하면
  (m+1) × (n+1) 크기의 DP 테이블 H를 만듭니다.

• 모든 셀을 0으로 초기화합니다.

  • 전역 정렬과 달리, 스미스–워터맨은 음수 점수를 허용하지 않기 때문에 0이 매우 중요합니다.

H[0][j] = 0
H[i][0] = 0

2) 점수 계산식

• 각 셀 (i, j)에서 가능한 세 가지 방향을 고려합니다.

1) 대각선 ↖ : H[i-1][j-1] + (MATCH or MISMATCH)
2) 위쪽   ↑ : H[i-1][j] + GAP
3) 왼쪽   ← : H[i][j-1] + GAP

• 이 중 가장 큰 값을 취하되, 음수일 경우 0으로 초기화합니다.

즉,

H[i][j] = max(
    0,
    H[i-1][j-1] + score(A[i], B[j]),
    H[i-1][j] + GAP,
    H[i][j-1] + GAP
)

• 이 “0”이 들어가는 부분이 바로 지역 정렬(Local alignment) 의 핵심입니다.

  • 점수가 0이 되는 순간, 새로운 지역 구간이 시작된다고 해석합니다.

3) 최댓값 찾기

• DP 테이블을 모두 채운 후, H[i][j] 값 중 가장 큰 값이 최적 지역 정렬 점수입니다.

  • 그 셀이 바로 최적 구간의 끝을 의미합니다.

4) 추적(Traceback)

• 최댓값 위치에서 시작해서 대각선(↖), 위(↑), 왼쪽(←)으로 거슬러 올라가며 점수가 0이 되는 지점까지 역추적합니다.

  • 이때 따라간 경로가 가장 유사한 지역 서열 구간을 나타냅니다.

4. 예시

A = "ACACACTA"
B = "AGCACACA"

• DP 계산 후 최댓값이 6이라면,해당 위치에서 역추적하면 예를 들어 이런 정렬이 나올 수 있습니다:

A: ACACACTA
B: AGCACACA
       ||||
       CACA  (local match)

• 즉, 전체 서열이 아니라 "CACA" 구간이 가장 유사한 부분으로 탐지됩니다.

5. 스미스–워터맨 vs 니들먼–운치 비교

구분	Smith–Waterman	Needleman–Wunsch
정렬 방식	지역 정렬 (부분 서열)	전역 정렬 (전체 서열)
초기화	전부 0	첫 행·열은 누적 gap
음수 점수	0으로 클리핑	음수 허용
사용 예시	유사 구간 탐색, BLAST	전체 서열 비교
최댓값	DP 내 임의의 위치	DP 마지막 셀 (끝점)

6. 파이썬 예시 코드

import numpy as np

def smith_waterman(seq1, seq2, match=1, mismatch=-1, gap=-2):
    m, n = len(seq1), len(seq2)
    H = np.zeros((m+1, n+1), dtype=int)
    max_score = 0
    max_pos = None

    # DP 테이블 채우기
    for i in range(1, m+1):
        for j in range(1, n+1):
            score_diag = H[i-1][j-1] + (match if seq1[i-1] == seq2[j-1] else mismatch)
            score_up = H[i-1][j] + gap
            score_left = H[i][j-1] + gap
            H[i][j] = max(0, score_diag, score_up, score_left)

            if H[i][j] > max_score:
                max_score = H[i][j]
                max_pos = (i, j)

    # Traceback
    i, j = max_pos
    aligned1, aligned2 = "", ""
    while i > 0 and j > 0 and H[i][j] > 0:
        if H[i][j] == H[i-1][j-1] + (match if seq1[i-1] == seq2[j-1] else mismatch):
            aligned1 = seq1[i-1] + aligned1
            aligned2 = seq2[j-1] + aligned2
            i -= 1; j -= 1
        elif H[i][j] == H[i-1][j] + gap:
            aligned1 = seq1[i-1] + aligned1
            aligned2 = "-" + aligned2
            i -= 1
        else:
            aligned1 = "-" + aligned1
            aligned2 = seq2[j-1] + aligned2
            j -= 1

    return max_score, aligned1, aligned2, H

6. DPX(Dynamic Programming eXtensions) 명령어

• Smith–Waterman의 셀 갱신 식을 Hopper(H100)에서 DPX( Dynamic Programming accelerators ) 내장 연산으로 묶어 주면, 전형적인 add + {min/max} + clamp(0) 패턴을 한 번에 처리할 수 있다.

• NVIDIA가 공개한 DPX SIMD 내장함수(인트린식) 예시는 다음과 같습니다.

  • __vimax3_s16x2_relu(a,b,c) → 반워드(16비트) 단위로 max(max(max(a,b),c), 0) 수행

  • __viaddmax_s16x2_relu(a,b,c) → 반워드 단위로 (a+b)와 c의 max, 그리고 ReLU(0 하한 클램프) 까지 한 번에 수행

  • __viaddmin_s16x2_relu(a,b,c) → 반워드 단위로 (a+b)와 c의 min, 그리고 ReLU 수행

• 이 인트린식들은 CUDA 12에서 DPX API로 노출되며, Hopper(Compute Capability 9.x)에서 하드웨어 가속되고 구세대에서는 소프트웨어 대체 경로가 사용됩니다. (NVIDIA Developer, NVIDIA Docs)

1) SW(로컬 정렬, affine gap)의 DPX 매핑 감각

• Affine gap 버전의 전형적 재귀식(점수는 16비트 정수 가정, ReLU는 로컬 정렬의 max(…,0)에 해당)

  • 치환/대각(매치·미스매치): M[i][j] = H[i-1][j-1] + s(x_i, y_j)

  • 삽입(위에서 내려옴)

    • I[i][j] = max(H[i-1][j] + go+ge, I[i-1][j] + ge)

  • 삭제(왼쪽에서 옴)

    • D[i][j] = max(H[i][j-1] + go+ge, D[i][j-1] + ge)

  • 최종 셀

    • H[i][j] = max(0, M[i][j], I[i][j], D[i][j])

• 여기서 go(gap open), ge(gap extend)는 음수 패널티고, 우리는 반워드 2개(s16x2)를 한꺼번에 갱신해 대역폭/스루풋을 끌어올립니다.

  • I/D 갱신은 “add 후 max” 패턴이므로 __viaddmax_s16x2_relu와 잘 맞고, 최종 H는 “3-way max + ReLU”라 __vimax3_s16x2_relu가 적합합니다.

2) 예시 CUDA C++ 커널 (s16x2로 2셀씩 갱신)

교육·시작용 미니멀 예시입니다. 실제 서비스 수준에선 타일링, 워프 간 동기화, 메모리 coalescing, anti-diagonal 처리, bank 충돌 회피, traceback 압축 저장 등을 추가하세요.

// nvcc -O3 -arch=sm_90a sw_dpx.cu -o sw_dpx
#include <cuda_runtime.h>
#include <stdint.h>

// DPX SIMD intrinsics (CUDA 12+; Hopper에서 HW 가속)
//  - __viaddmax_s16x2_relu(a,b,c): per-halfword ReLU(max(a+b, c))
//  - __vimax3_s16x2_relu(a,b,c):   per-halfword ReLU(max(a,b,c))
extern "C" __device__ unsigned int __viaddmax_s16x2_relu(unsigned int, unsigned int, unsigned int);
extern "C" __device__ unsigned int __vimax3_s16x2_relu(unsigned int, unsigned int, unsigned int);

// 유틸: s16x2 pack/unpack
__device__ inline unsigned pack_s16x2(short lo, short hi) {
    return (unsigned)((uint16_t)lo | ((uint32_t)(uint16_t)hi << 16));
}
__device__ inline short lo_s16(unsigned u){ return (short)(u & 0xFFFF); }
__device__ inline short hi_s16(unsigned u){ return (short)((u >> 16) & 0xFFFF); }

// 간단한 점수표: match=+2, mismatch=-1 (16비트 안전)
__device__ inline short sub_score(char a, char b) { return (a==b) ? 2 : -1; }

// 커널 가정:
//  - 한 워프가 한 anti-diagonal 스트립을 담당 (데모 목적)
//  - H/I/D는 s16로 저장 (점수 범위 확인 필수)
//  - traceback은 생략 (필요 시 방향 비트패킹 버퍼 추가)
__global__ void sw_dpx_kernel(
    const char* __restrict__ A, int M,
    const char* __restrict__ B, int N,
    short gap_open, short gap_ext,
    short* __restrict__ H,  // (M+1) x (N+1)
    short* __restrict__ I,
    short* __restrict__ D)
{
    // 간단화를 위해: 각 스레드가 (i,j)와 (i,j+1) 두 셀(s16x2)을 한 번에 처리한다 가정
    int j = (blockIdx.x * blockDim.x + threadIdx.x) * 2 + 1; // 1..N-1
    int i = blockIdx.y + 1;                                  // 1..M

    if (i > M || j > N) return;

    // 이전 셀 값 로드
    // 인덱싱: row-major, pitch = (N+1)
    int pitch = N + 1;

    // 상( i-1, j ), ( i-1, j+1 )
    short H_up0 = H[(i-1)*pitch + j];
    short H_up1 = (j+1 <= N) ? H[(i-1)*pitch + (j+1)] : 0;
    short I_up0 = I[(i-1)*pitch + j];
    short I_up1 = (j+1 <= N) ? I[(i-1)*pitch + (j+1)] : (short)0;

    // 좌( i, j-1 ), ( i, j )
    short H_lt0 = H[i*pitch + (j-1)];
    short H_lt1 = H[i*pitch + j];
    short D_lt0 = D[i*pitch + (j-1)];
    short D_lt1 = D[i*pitch + j];

    // 대각( i-1, j-1 ), ( i-1, j )
    short H_dg0 = H[(i-1)*pitch + (j-1)];
    short H_dg1 = H[(i-1)*pitch + j];

    // 서브스코어 계산 (두 칸 패킹)
    short s0 = sub_score(A[i-1], B[j-1]);
    short s1 = (j+1 <= N) ? sub_score(A[i-1], B[j]) : (short)-1;
    unsigned S = pack_s16x2(s0, s1);

    // 상방향 갭 갱신: I = max(H_up + go+ge, I_up + ge), ReLU(0) 불필요 (음수가 유효) → 하지만
    // 최종 H에서 ReLU 처리하므로 중간 I/D는 음수 허용. 여기서는 viaddmax_relu를 써도 무방(0클램프가 들어감).
    //  -> 정확하게 음수를 유지하려면 _relu가 없는 변형을 쓰는게 이상적이나, 공개 API는 _relu변형이 대표적.
    //     교육용 예시: 0 하한이 들어가도 보통 gap이 음수 패널티이므로 max(…,0)이 H에서 걸리기 전에 I/D가 0에 눌릴 수 있음.
    //     실제 프로덕션에선 CUDA 버전에 따라 _relu 없는 변형/정밀 흐름을 선택하거나 오프셋을 더해 양수영역으로 치우치는 구현을 고려하세요.

    short go_ge = gap_open + gap_ext; // 음수
    unsigned V_go_ge = pack_s16x2(go_ge, go_ge);
    unsigned V_ge    = pack_s16x2(gap_ext, gap_ext);

    unsigned V_Hup   = pack_s16x2(H_up0, H_up1);
    unsigned V_Iup   = pack_s16x2(I_up0, I_up1);
    unsigned V_Hlt   = pack_s16x2(H_lt0, H_lt1);
    unsigned V_Dlt   = pack_s16x2(D_lt0, D_lt1);
    unsigned V_Hdg   = pack_s16x2(H_dg0, H_dg1);

    // I 갱신: max(H_up + go+ge, I_up + ge)
    unsigned I_cand1 = __viaddmax_s16x2_relu(V_Hup, V_go_ge, V_Iup); // ReLU 포함
    unsigned I_new   = __viaddmax_s16x2_relu(V_Iup, V_ge,    I_cand1);

    // D 갱신: max(H_lt + go+ge, D_lt + ge)
    unsigned D_cand1 = __viaddmax_s16x2_relu(V_Hlt, V_go_ge, V_Dlt);
    unsigned D_new   = __viaddmax_s16x2_relu(V_Dlt, V_ge,    D_cand1);

    // 대각 매치/미스매치: M = H_dg + S
    // (ReLU는 H에서 처리)
    short M0 = (short)(H_dg0 + s0);
    short M1 = (short)(H_dg1 + s1);
    unsigned V_M = pack_s16x2(M0, M1);

    // 최종 H: max(0, M, I, D) → 3-way max + ReLU (M vs I vs D) 후 0과도 max
    // vimax3_relu가 (a,b,c,0)을 모두 처리
    unsigned H_tmp = __vimax3_s16x2_relu(V_M, I_new, D_new);

    // 결과 저장
    short H0 = lo_s16(H_tmp), H1 = hi_s16(H_tmp);
    short I0 = lo_s16(I_new), I1 = hi_s16(I_new);
    short D0 = lo_s16(D_new), D1 = hi_s16(D_new);

    H[i*pitch + j] = H0;
    if (j+1 <= N) H[i*pitch + (j+1)] = H1;

    I[i*pitch + j] = I0;
    if (j+1 <= N) I[i*pitch + (j+1)] = I1;

    D[i*pitch + j] = D0;
    if (j+1 <= N) D[i*pitch + (j+1)] = D1;
}

// 호스트 래퍼(데모용): 그리드/블록 구성은 시퀀스 길이에 맞게 조정
void launch_sw_dpx(const char* d_A, int M, const char* d_B, int N,
                   short go, short ge, short* d_H, short* d_I, short* d_D,
                   cudaStream_t stream=0)
{
    dim3 block(128, 1, 1);                  // 128스레드 → j를 2칸씩 처리
    dim3 grid((N + 1 + block.x*2 - 1)/(block.x*2), M, 1);
    sw_dpx_kernel<<<grid, block, 0, stream>>>(d_A, M, d_B, N, go, ge, d_H, d_I, d_D);
}

빌드/런 팁

• 컴파일: nvcc -O3 -arch=sm_90a sw_dpx.cu -o sw_dpx
  (H100은 sm_90a/sm_90 계열. 로컬 환경에 맞춰 지정)
• CUDA 12+에서 DPX 인트린식이 제공되며 Hopper에서 하드웨어 가속. 구세대 GPU에서는 소프트웨어 에뮬레이션 경로라 속도 이점이 줄어듭니다. (NVIDIA Docs)
• 점수 범위가 int16을 넘지 않도록 go, ge, match/mismatch와 서열 길이 상한을 조절하세요(오버플로 방지). CUDASW++4.0 같은 최신 구현은 DPX 활용 + 타일링/패킹 최적화를 통해 큰 이득을 얻습니다. (BioMed Central)

3) 정확도/성능 관련 주의

1. ReLU의 위치

   • 위 예시는 교육용으로 I/D 갱신에도 _relu 변형을 사용했지만, 이론적으로는 I/D 상태값이 음수도 유효합니다(최종 H에서만 0 하한).

   • CUDA 버전에 따라 _relu 없는 변형을 선택하거나, 내부 점수에 상수 오프셋을 더해 양수 영역에서 연산한 뒤 마지막에 오프셋 제거하는 테크닉을 쓰면 수학적으로 더 깔끔합니다. (공식 블로그는 _relu 변형을 SW에서 적극 활용하는 예시를 보여줍니다.)

2. 패킹과 동시성

   • 여기선 s16x2로 “가로 2셀”을 처리했지만, 실제론 anti-diagonal 파이프라이닝, 타일 단위 공유메모리 캐싱, 워프 셔플 등을 조합해야 메모리 병목을 줄이고 DPX의 장점을 극대화할 수 있습니다. CUDASW++4.0은 이 부분을 정교하게 구현합니다.

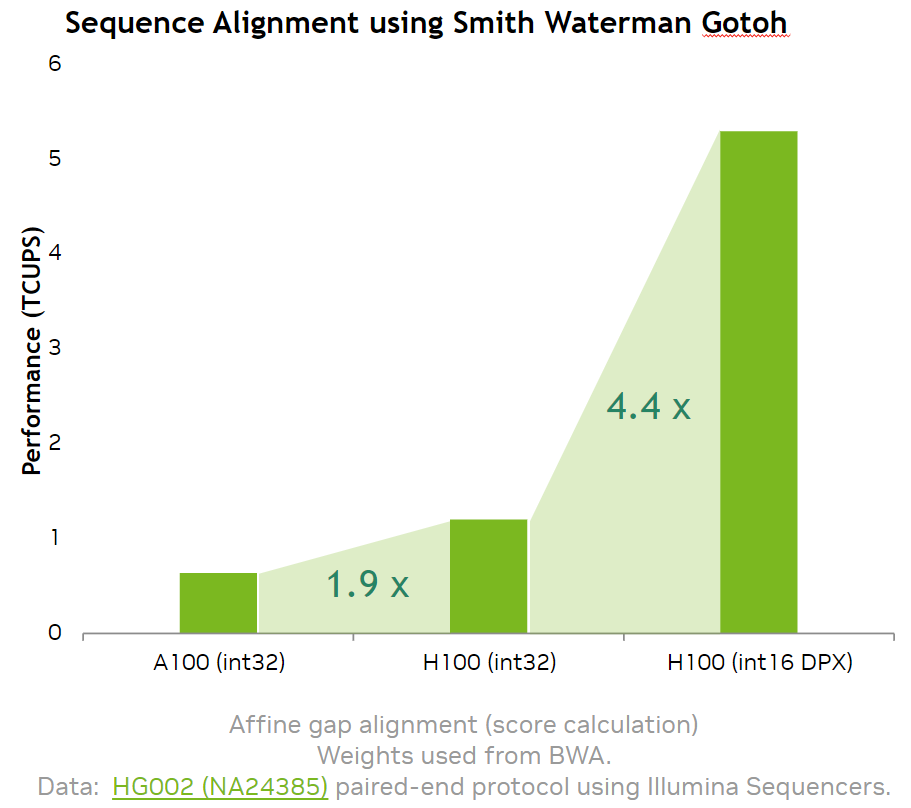
3. 스피드업 기대치

   • NVIDIA는 H100에서 SW 스코어링 단계가 A100 대비 ~7–8× 가속된다고 보고합니다(내부 루프 DPX화).

     • 워크로드/길이/구현에 따라 달라집니다.