[머신러닝] PCA(Principal Component Analysis / iris, wine, eigenface, HAR, MNIST, 타이타닉 데이터 )
제로베이스 데이터스쿨

✍🏻 3일, 4일 공부 이야기.
오늘 실습한 내용은 위 깃허브 사진을 클릭하면 이동됩니다 :)
PCA(Principal Component Analysis)
PCA(주성분 분석)는 데이터 집합 내에 존재하는 각 데이터의 차이를 가장 잘 나타내주는 요소를 찾아내는 방법이다. 주로 통계 데이터분석(주성분 찾기), 데이터 압축(차원 감소), 노이즈 제거 등의 분야에서 사용되고 있다.
차원 축소(Dimensionality Reduction)와 변수 추출(Feature Extraction) 기법으로 널리 쓰이고 있는데 PCA(주성분 분석)는 데이터의 분산을 최대한 보존하면서 서로 직교하는 새 축을 찾아 고차원 공간의 표본들을 선형 연관성이 없는 저차원의 공간으로 변환하는 기법이다.
이때 변수 추출(Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법으로서 변수 선택(Feature Selectrion)과는 다르다는 것을 알아야한다.
sklearn
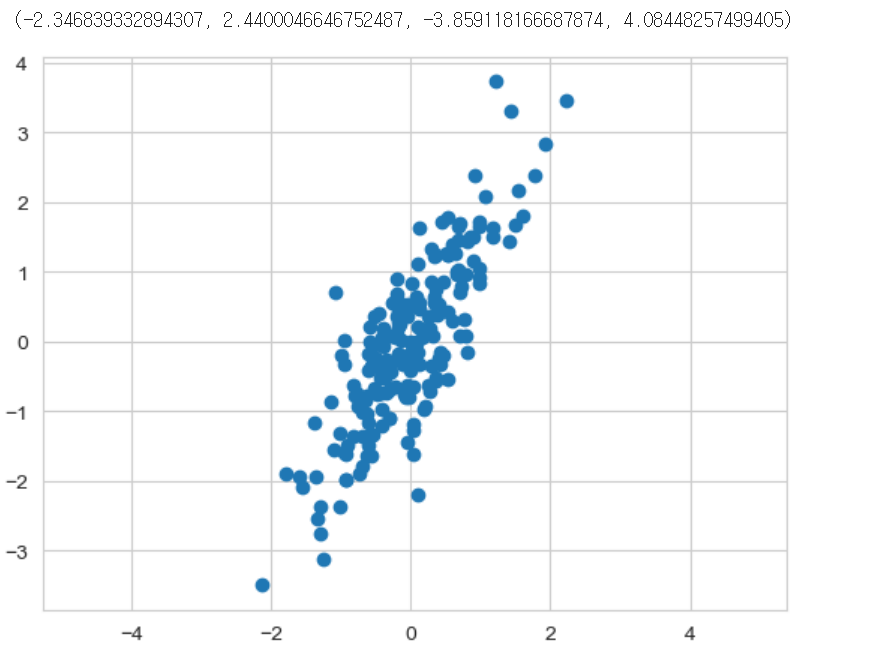
(200,2)의 shape을 가지는 난수를 발생시키고 해당 데이터를 2개의 주성분으로 표현해보자.
# np.random.rand : 0 - 1 사이 균일 분포에서의 난수
# np.random.randn : 가우시안 표준 정규분포에서의 난수
rng = np.random.RandomState(13)
X = np.dot(rng.rand(2, 2) , rng.randn(2, 200)).T
sns.set_style('whitegrid')
plt.scatter(X[:,0], X[:,1])
plt.axis('equal') # x축과 y축의 1 간격을 같게 조정💻 출력
위와 같은 데이터가 만들어졌다. 모든 데이터를 단 2개의 벡터로 표현하는 것이 주성분 분석이다.
# n_components : 표시될 주성분 개수
from sklearn.decomposition import PCA
pca = PCA(n_components= 2, random_state=13)
pca.fit(X)2개의 주성분으로 학습된 pca 변수에는 다음과 같은 인사이트를 얻어낼 수 있다.
-
pca.components_
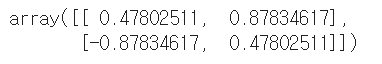
2행의 행렬이 반환되었고, 각 반환된 행은 하나의 주성분이 된다. -
pca.explained_variance_
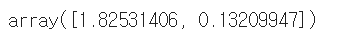
: 각 주성분의 설명력 -
pca.explained_variance_ratio_
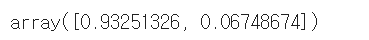
: 각 주성분의 설명력의 비율 -
pca.mean_
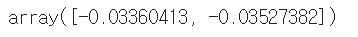
: 주성분의 평균으로 시작점이 됨
def draw_vector(v0, v1, ax = None):
# 그림을 그릴 matplotlib 축
ax = ax or plt.gca()
# 화살표 스타일 설정
arrowprops = dict(
arrowstyle = '->', # 화살표 스타일
linewidth = 2, # 선 굵기
color = 'black', # 색상
# 시작점(v0)과 끝점(v1)에서 선 길이를 줄이는 비율
shrinkA = 0,
shrinkB = 0,
)
# 텍스트 없이 그려짐, 점 위치 , 점 위치, 화살표 속성
ax.annotate('', v1, v0, arrowprops = arrowprops)
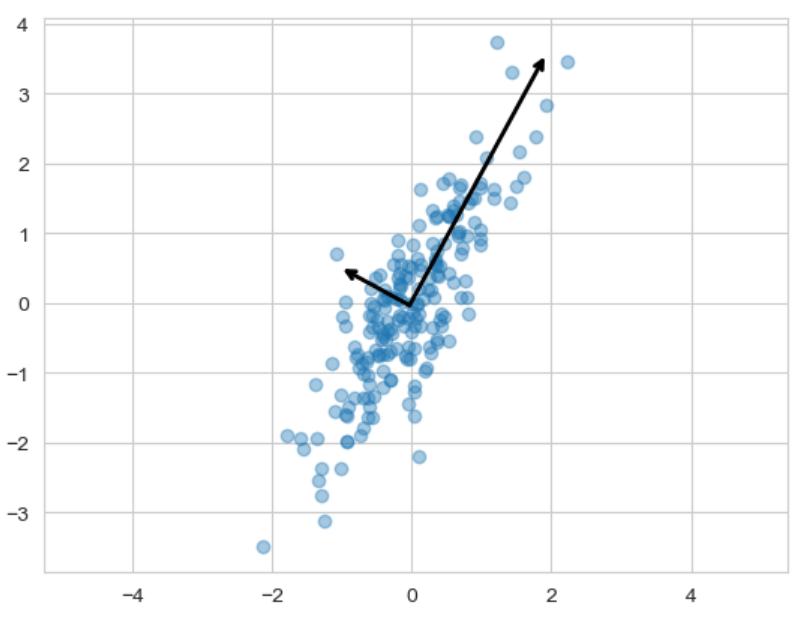
plt.scatter(X[:, 0], X[:, 1], alpha=0.4)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length) # 3배는 화살표가 보이기 위해 임의로 설정한 값
# pca.mean_ : 각 벡터에 대한 시작점
# pca.mean_ + v : 끝점
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')
plt.show()💻 출력
주성분을 그리는 함수를 만들어주고 출력하면 두 화살표를 통해 모든 데이터를 표현하는 주성분이 만들어졌다.
주성분은 기존의 축을 주성분으로 바꾸는 주축 변경도 가능하다.
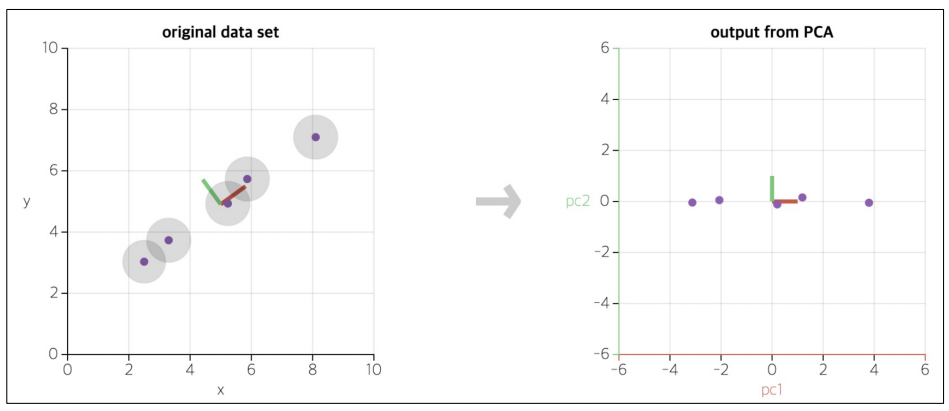
그동안 연습했던 여러 데이터들을 주성분 분석도 해보자.
iris 데이터
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
iris_pd = pd.DataFrame(iris.data, columns = iris.feature_names)
iris_pd['species'] = iris.target
sns.pairplot(iris_pd, hue = 'species', height = 3,
x_vars = ['sepal length (cm)', 'petal length (cm)'],
y_vars = ['sepal width (cm)', 'petal width (cm)'])데이터를 읽고 모든 데이터로 일단 pariplot을 그리면 아래와 같다.
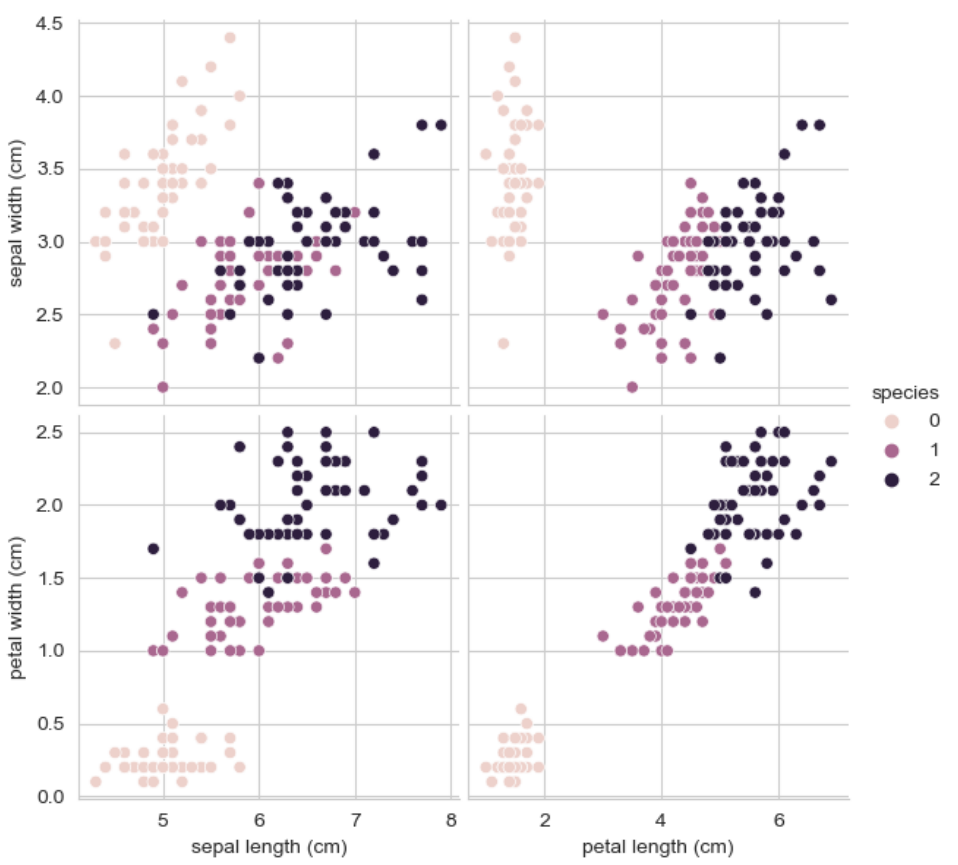
특성 4개로 각 꽃을 분류해보기엔 어려워보인다.
2개의 주성분으로 특성 4개를 줄여보자.
먼저, PCA에서는 Scaler의 적용이 꽤 큰 효과를 불러일으키기 때문에 StandardScaler를 fit시킨 후 주성분 분석을 실시할 것이다.
from sklearn.preprocessing import StandardScaler
iris_ss = StandardScaler().fit_transform(iris.data)그리고 pca의 결과를 반환하는 함수와 그 결과를 데이터프레임으로 반환하는 함수를 만들어주었다.
from sklearn.decomposition import PCA
def get_pca_data(ss_data, n_components = 2):
pca = PCA(n_components= n_components)
pca.fit(ss_data)
return pca.transform(ss_data), pca
def get_pd_from_pca(pca_data, cols = ['pca_component_1', 'pca_component_2']):
return(pd.DataFrame(pca_data, columns = cols))앞서 Scaler를 적용한 데이터에 pca를 적용해보자.
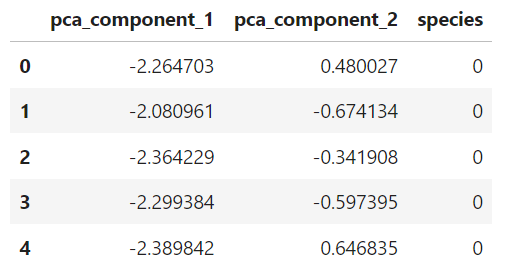
# 변환
iris_pca, pca = get_pca_data(iris_ss, 2)
# iris_pca.shape #(150, 2)
iris_pd_pca = get_pd_from_pca(iris_pca)
iris_pd_pca['species'] = iris.target
iris_pd_pca.head()💻 출력
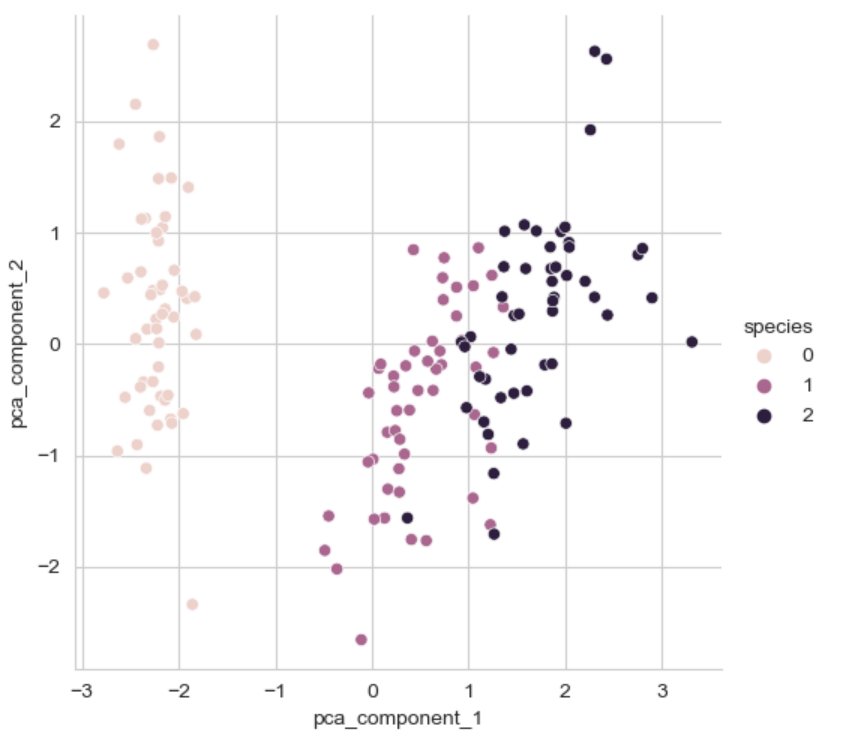
sns.pairplot(iris_pd_pca, hue = 'species', height = 5,
x_vars = ['pca_component_1'],
y_vars = ['pca_component_2'])💻 출력
그리고 시각화해보면 4개의 특성으로 그린 pairplot보단, 좀 더 분류하기 쉬워보인다.
2가지의 특성을 이용했을 때의 설명력은 pca.explained_variance_ratio_를 통해 array([0.72962445, 0.22850762])라는 결과값이 나왔다. 머신러닝에 적용하면 어떨까?
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
def rf_scores(X, y, cv = 5):
rf = RandomForestClassifier(random_state= 13, n_estimators=100)
scores_rf = cross_val_score(rf, X, y, scoring = 'accuracy', cv = cv)
print("Score : ", np.mean(scores_rf))
# 4가지 특성을 모두 사용한 randomforest
# iris_ss : Standard Scaler만 적용한 iris
print(rf_scores(iris_ss, iris.target))
# 주성분 분석을 적용한 randomforest(2가지 특성 이용)
pca_X = iris_pd_pca[['pca_component_1', 'pca_component_2']]
print(rf_scores(pca_X, iris.target))💻 출력
Score : 0.96
Score : 0.9066666666666666
데이터를 100% 반영한 것이 아니기 떄문에 정확도는 떨어질 수 밖에 없다. 하지만 데이터를 줄여서 머신러닝을 돌릴 수 있다는 인사이트를 얻어가자.
wine 데이터
앞서 wine 데이터는 feature가 여러 개였다. 레드 와인인지, 화이트 와인인지 구분하기 위해 주성분 분석과 머신러닝을 돌려보자.
데이터를 읽고 StandardScaler를 적용시키면 아래와 같다.
wine_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/wine.csv'
wine = pd.read_csv(wine_url, sep = ',', index_col=0)
# 와인 색상 분류를 하기 위해 타겟 데이터를 'color' 컬럼으로 정함
wine_y = wine['color']
wine_X = wine.drop(['color'], axis = 1)
# StandardScaler
wine_ss = StandardScaler().fit_transform(wine_X)pca_wine, pca = get_pca_data(wine_ss, n_components=2)
# pca_wine.shape #(6497,2)
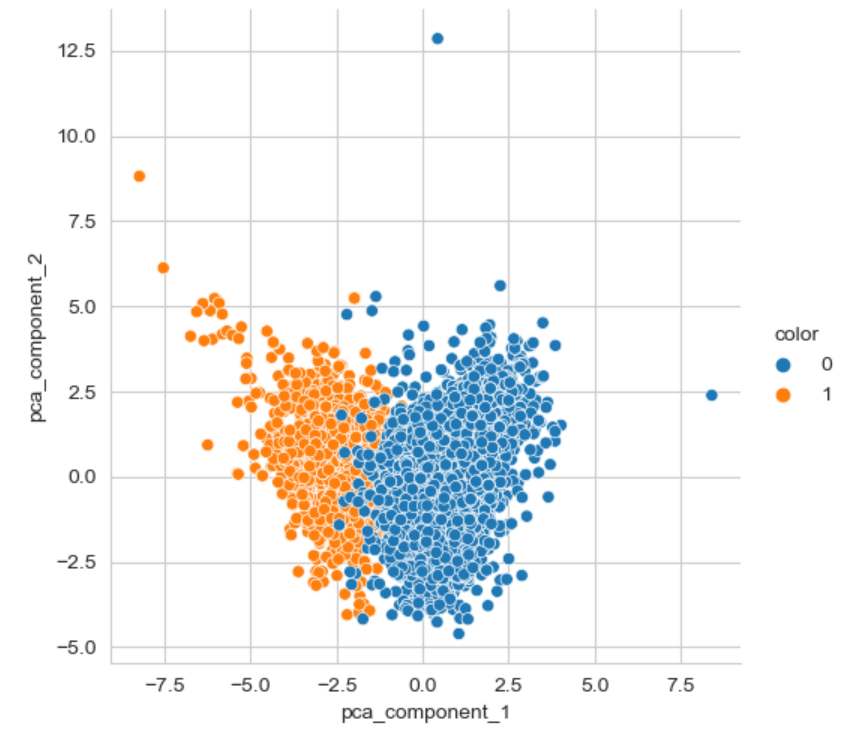
pca.explained_variance_ratio_ wine 데이터는 총 12개의 컬럼을 가지고 있는데, 2개의 주성분으로 줄여보았다. 이 때 설명력은 array([0.25346226, 0.22082117]) 가 나왔다. 총 설명력이 50%도 되지 않아 분석으로 적당해 보이진 않았지만, 그래도 시각화해보자.
pca_columns = ['pca_component_1', 'pca_component_2']
pca_wine_pd = pd.DataFrame(pca_wine, columns = pca_columns)
pca_wine_pd['color'] = wine_y.values
sns.pairplot(pca_wine_pd, hue = 'color', height = 5,
x_vars=['pca_component_1'], y_vars = ['pca_component_2'])💻 출력
설명력은 좋지 않았지만, 시각화된 것을 보았을 땐 그리 나빠 보이진 않는다! 한 번 머신러닝을 돌려보자.
- 주성분 분석없이
StandardScaler만 돌린RandomForest# StandardScaler만 적용된 원 데이터로 돌린 rf rf_scores(wine_ss, wine_y)💻 출력
Score : 0.9935352638124
- 2개의 PCA로 변환한 데이터로 돌린
RandomForest# 2개의 pca로 변환한 데이터로 돌린 rf pca_X = pca_wine_pd[['pca_component_1', 'pca_component_2']] rf_scores(pca_X, wine_y)💻 출력
Score : 0.981067803635933
머신러닝 성능에는 큰 차이가 없어보인다.
이번에는 주성분 3개로 표현해보자.
pca_wine, pca = get_pca_data(wine_ss, n_components=3)
print(pca.explained_variance_ratio_ )
pca_columns = ['pca_component_1', 'pca_component_2', 'pca_component_3']
pca_wine_pd = pd.DataFrame(pca_wine, columns = pca_columns)
pca_wine_pd['color'] = wine_y.values
pca_X = pca_wine_pd[['pca_component_1', 'pca_component_2', 'pca_component_3']]
rf_scores(pca_X, wine_y)💻 출력
[0.25346226 0.22082117 0.13679223]
Score : 0.9832236631728548
설명력도 60%로 올랐고 98%의 정확도도 보였다.
3개의 특성으로 12개의 특성을 대신할 수 있게 되었다.
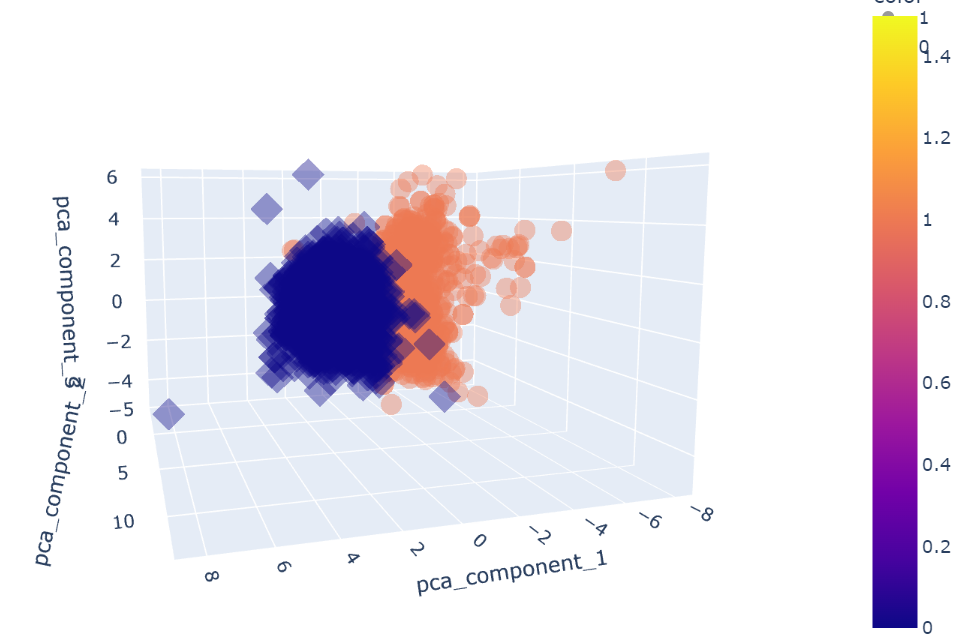
import plotly_express as px
fig = px.scatter_3d(pca_wine_pd, x = 'pca_component_1', y = 'pca_component_2', z = 'pca_component_3',
color = 'color', symbol = 'color', opacity=0.4)
fig.update_layout(margin = dict(l = 0, r = 0, b = 0, t = 0))
fig.show()💻 출력
PCA eigenface(표정 이미지)
pca eigenface 는 사람들의 얼굴 이미지를 분석하여 표정을 찾아볼 수 있는 PCA 의 재밌는 예시이다.
우리는 여기서 특정 인물(20번째 인물 , olivetti)의 10장 사진만 실습해볼 예정이다.
from sklearn.datasets import fetch_olivetti_faces
faces_all = fetch_olivetti_faces()
# 특정 인물 선택
K = 20 # 인덱스가 20인 인물 선택
faces = faces_all.images[faces_all.target == K]
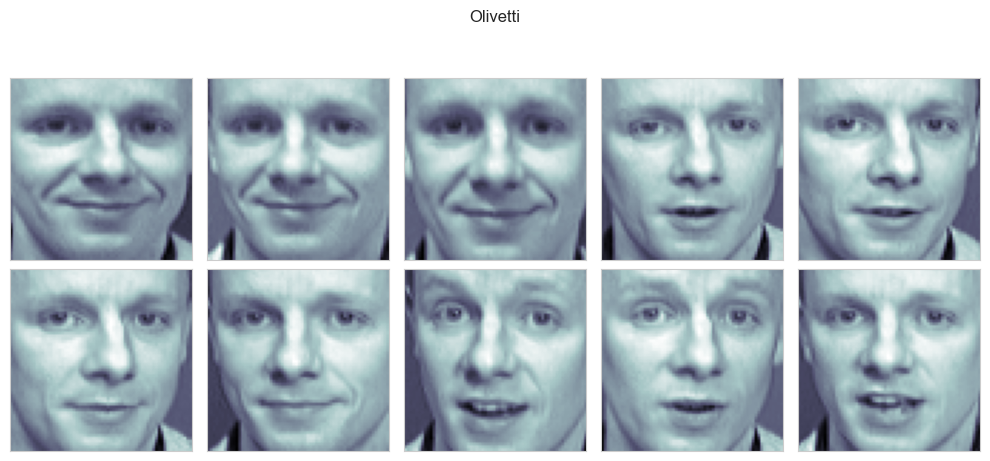
# faces.shape # (10,64,64)데이터를 읽어들였는데 해당 데이터가 어떻게 생긴 것인지 살펴보자.
import matplotlib.pyplot as plt
# 2행 5열로 그림을 그리고자 함
N = 2
M = 5
fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top = 1, hspace = 0, wspace= 0.05)
for n in range(N*M):
ax = fig.add_subplot(N, M, n+1)
ax.imshow(faces[n], cmap = plt.cm.bone)
ax.grid(False)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
plt.suptitle('Olivetti')
plt.tight_layout()
plt.show()💻 출력
여러 표정의 10장의 사진이 들어가있다.
이 사진을 2개의 주성분으로 분리시켜 모든 사진을 표현해보도록 하자.
from sklearn.decomposition import PCA
pca = PCA(n_components= 2)
X = faces_all.data[faces_all.target == K] # Olivetti 데이터
W = pca.fit_transform(X)
X_inv = pca.inverse_transform(W)
X.shape, W.shape, X_inv.shape, faces.shape💻 출력
(10, 4096) (10, 2) (10, 4096) (10, 64, 64)
X는 10장의 데이터가 64*64 픽셀로 이루어진 데이터로 보인다. 이미지 데이터는 픽셀을 맞춰주는 것이 중요하기 때문에 이렇게 shape을 확인하는 것이 중요하다.
주성분 분석한 2개의 특성으로 이미지를 그려보자면 기존의 그림(faces)이 64*64 픽셀로 이루어졌으니 X_inv를 reshape 해준 후 그려주어야한다.
# 결과 확인
N = 2
M = 5
fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top = 1, bottom = 0, hspace = 0, wspace= 0.05)
for n in range(N*M):
ax = fig.add_subplot(N, M, n+1)
# 기존 shape으로 돌려줘야함
ax.imshow(X_inv[n].reshape(64,64), cmap = plt.cm.bone)
ax.grid(False)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
plt.suptitle('PCA result Olivetti')
plt.tight_layout()
plt.show()💻 출력
사진이 약간 뭉그뜨려진 느낌이 있지만 표정은 대체로 잘 표현된 듯하다.
도대체 component 변수에는 무슨 역할을 하는 것이 저장되어있는 것일까?
face_mean = pca.mean_.reshape(64,64)
face_p1 = pca.components_[0].reshape(64,64)
face_p2 = pca.components_[1].reshape(64,64)
# 첫번째 그림
plt.figure(figsize=(12,7))
plt.subplot(131)
plt.imshow(face_mean, cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([]); plt.title("mean")
# 두번째 그림
plt.subplot(132)
plt.imshow(face_p1, cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([]); plt.title("face_p1")
# 세번째 그림
plt.subplot(133)
plt.imshow(face_p2, cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([]); plt.title("face_p2")
plt.show()💻 출력
pca_mean , pca.comonents_[0], pca.comonents_[1] 변수를 그려보았다. 우리가 가진 10장의 데이터는 face_mean에서 face_p1, face_p2를 더한 것을 통해 모두 표현되는 것이다.
해당 주성분이 얼만큼 표현되는지에 대한 가중치를 설정하고 face_mean에서 해당 가중치를 face_p1에 곱한 값을 더해 10장의 사진을 다시 그려보았다.
N = 2
M = 5
# 우리는 10장을 그릴 것이다.
w = np.linspace(-5, 10, N*M) # -5부터 10까지 10개의 숫자
# 첫번째 성분 변화
fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top = 1, bottom = 0, hspace=0,wspace=0.05)
for n in range(N*M):
ax = fig.add_subplot(N, M, n+1)
# face_mean에서 face_p1에 가중치를 곱해서 더한 데이터
ax.imshow(face_mean + w[n] * face_p1, cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([])
plt.title('Weight : ' + str(round(w[n])))
plt.tight_layout()
plt.show()💻 출력
# 두번째 성분 변화
fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top = 1, bottom = 0, hspace=0,wspace=0.05)
for n in range(N*M):
ax = fig.add_subplot(N, M, n+1)
# face_mean에서 face_p2에 가중치를 곱해서 더한 데이터
ax.imshow(face_mean + w[n] * face_p2, cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([])
plt.title('Weight : ' + str(round(w[n])))
plt.tight_layout()
plt.show()💻 출력
주성분을 조금씩 변화시켜보니 원본 데이터의 모습이 살짝 보이는 것 같다.
이번에는 두 주성분을 한 번에 표현해보자.
nx, ny = (5,5)
x = np.linspace(-5, 8, nx)
y = np.linspace(-5, 8, ny)
# 앞서 추출한 가중치를 meshgrid 형태로 추출
w1, w2 = np.meshgrid(x, y)
# 이미지와 결합시키기 위한 reshape
w1 = w1.reshape(-1,)
w2 = w2.reshape(-1,)
fig = plt.figure(figsize=(10,5))
plt.subplots_adjust(top = 1, bottom = 0, hspace=0,wspace=0.05)
for n in range(N*M):
ax = fig.add_subplot(N, M, n+1)
# face_mean에서 face_p1에 가중치를 곱해서 더한 데이터
ax.imshow(face_mean + w1[n] * face_p1 + w2[n] * face_p2 , cmap = plt.cm.bone)
plt.grid(False); plt.xticks([]); plt.yticks([])
plt.title(str(round(w1[n])) + ' , ' + str(round(w2[n])))
plt.tight_layout()
plt.show()💻 출력
두 주성분의 가중치를 변화해가며 그려보았는데 이는 아래와 같은 의미를 가진다.

MNIST

필기체 인식을 위해 제공된 데이터 NIST에서 숫자 데이터만 모아둔 것이 MNIST 데이터셋이다.
캐글에서 CSV 파일을 다운받아 사용해도 되고 라이브러리를 불러서 사용할 수도 있다.
28*28 픽셀의 0 - 9사이의 숫자 이미지와 레이블로 구성되어 있으며, 6만개의 훈련용 셋과 1만개의 실험용 셋으로 구성되어있다.
df_train = pd.read_csv('./data/mnist_train.csv')
df_test = pd.read_csv('./data/mnist_test.csv')
X_train = np.array(df_train.iloc[:, 1:])
y_train = np.array(df_train['label'])
X_test = np.array(df_test.iloc[:, 1:])
y_test = np.array(df_test['label'])데이터를 읽고 분리해 주었다.
먼저 데이터가 어떻게 생겼는지 봐보자.
6만개의 훈련용 데이터 셋 중 16개의 데이터만 랜덤으로 살펴보자.
import random
samples = random.choices(population=range(0,60000), k = 16)
import matplotlib.pyplot as plt
plt.figure(figsize=(14,12))
for idx, n in enumerate(samples):
plt.subplot(4, 4, idx + 1)
plt.imshow(X_train[n].reshape(28,28), cmap = "Greys", interpolation = 'nearest')
plt.title(y_train[n])
plt.show()💻 출력
랜덤으로 뽑은 16개의 숫자의 인덱스를 가진 데이터를 뽑아봤다.
이제 필기체 데이터를 넣으면 무슨 숫자인지 알아맞추는 모델을 만들기 위해 PCA와 KNN을 적용시켜보자.
먼저 KNN만 적용시킨 결과는 아래와 같다.
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors= 5)
clf.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
pred = clf.predict(X_test)
accuracy_score(y_test, pred)💻 출력
0.9688
96% 의 꽤 좋은 성능을 보여준다. 하지만 KNN은 모든 거리를 계산해야하기 때문에 시간이 오래 걸릴 수도 있다. 위 코드를 실행시키는 데에 20.5초 정도 소요되었다.
만약 특성이 많은 데이터라면 소요되는 시간은 무한대로 늘어날 것이다. 이를 차원의 저주라 하는데 이때 필요한 것이 차원을 줄여주는 PCA이다.
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.model_selection import GridSearchCV, StratifiedKFold
pipe = Pipeline([
('pca', PCA()),
('clf', KNeighborsClassifier())
])
parameters = {
'pca__n_components' : [2,5,10],
'clf__n_neighbors' : [5,10,15]
}
kf = StratifiedKFold(n_splits= 5, shuffle= True, random_state=13)
grid = GridSearchCV(pipe, parameters, cv = kf, n_jobs= -1, verbose = 1)
grid.fit(X_train, y_train)
pred = grid.best_estimator_.predict(X_test)
accuracy_score(y_test, pred)💻 출력
0.9289
성능이 조금 줄었지만 앞서 20.5초가 걸렸던 코드가 2초로 엄청 줄었다.
# 결과 확인
def results(y_pred, y_test):
from sklearn.metrics import classification_report, confusion_matrix
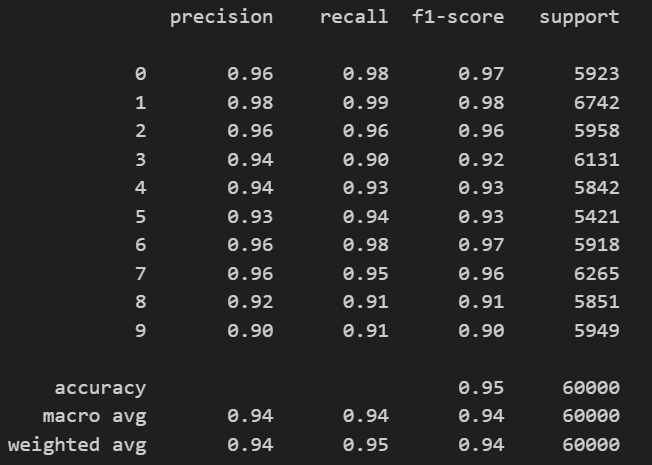
print(classification_report(y_test, y_pred))
results(grid.predict(X_train), y_train)💻 출력
실제로 결과가 어떤지 보았는데 대체로 골고루 잘 맞추고 있는 것 같다.
잘못 예측한 데이터도 몇 개 살펴보았는데 그건 깃허브에 올려두었으니 관심있으면 참고하기!!
타이타닉
titanic_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/titanic.xls'
titanic = pd.read_excel(titanic_url)titanic 데이터를 부르고 앞서 분석에서 꽤 중요한 역할을 해주었던 title(신분) 컬럼을 추가하고 ['Miss', 'Rare_m', 'Mr', 'Mrs', 'Rare_f'] 의 데이터로 분류해주었다.
그리고 머신러닝을 돌리기 위해선 문자열 데이터들이 숫자형으로 표현되어야하기 때문에 sex 컬럼과 title 컬럼을 LabelEncoder를 돌려 각각 gender, grade 컬럼에 저장해주었다.
from sklearn.preprocessing import LabelEncoder
# gender 컬럼 생성
le_sex = LabelEncoder()
le_sex.fit(titanic['sex'])
titanic['gender'] = le_sex.transform(titanic['sex'])
# grade 컬럼 생성
le_grade = LabelEncoder()
le_grade.fit(titanic['title'])
titanic['grade'] = le_grade.transform(titanic['title'])그리고 age와 fare 컬럼에 null이 들어간 데이터는 제외하고 Train/Test 셋으로 구분해주었다.
# null 데이터 제외
titanic = titanic[titanic['age'].notnull()]
titanic = titanic[titanic['fare'].notnull()]
# 데이터 분리
from sklearn.model_selection import train_test_split
X = titanic[['pclass', 'age', 'sibsp', 'parch', 'fare', 'gender', 'grade']].astype('float')
y = titanic['survived']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2, random_state=13)이제 주성분 분석 후 KNN을 적용시켜보자.
# 7개의 컬럼을 2개의 주성분으로 변환
pca_data, pca = get_pca_data(X_train, n_components= 2)
print_variance_ratio(pca)💻 출력
variance_ratio : [0.93576422 0.0632686 ]
sum of variance_ratio : 0.9990328289217747
2개의 주성분으로 분석했을 때 설명력이 99%이다...(??) 한 번 시각화해보자.
pca_pd = get_pd_from_pca(pca_data, pca.components_.shape[0])
pca_pd['survived'] = y_train
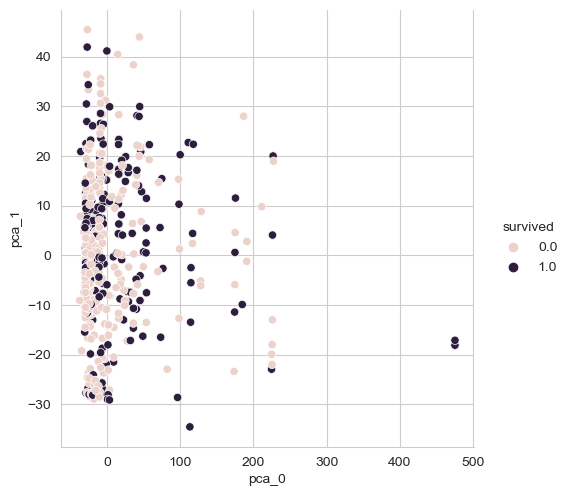
sns.pairplot(pca_pd, hue = 'survived', height = 5, x_vars = ['pca_0'], y_vars = ['pca_1'])💻 출력
위 시각화만 보았을 땐 생존 여부의 구분이 쉬울 것 같아보이진 않는다. 3개의 주성분으로 변환시켜보자.
pca_data, pca = get_pca_data(X_train, n_components= 3)
pca_pd = get_pd_from_pca(pca_data, pca.components_.shape[0])
pca_pd['survived'] = y_train
import plotly.express as px
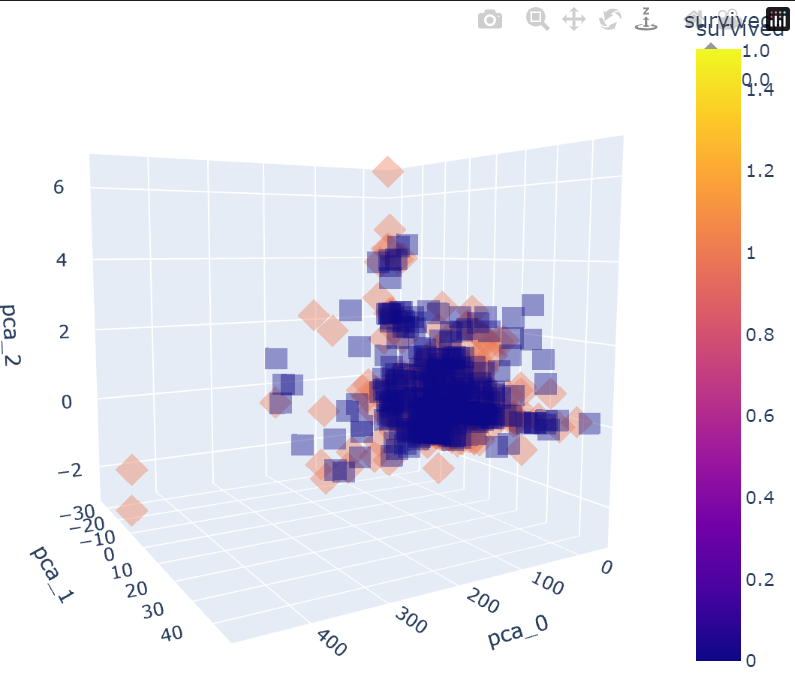
fig = px.scatter_3d(pca_pd, x = 'pca_0', y = 'pca_1', z = 'pca_2',
color = 'survived', symbol = 'survived',
opacity= 0.4)
fig.update_layout(margin = dict(l = 0, r = 0, b = 0, t =0))
fig.show()💻 출력
3차원의 그림은 이렇게 plotly를 이용하면 더 입체적으로 그릴 수 있다.
# pipeline 으로 survivied 예측
estimators = [
('scaler' , StandardScaler()),
('pca', PCA(n_components=3)),
('clf', KNeighborsClassifier(n_neighbors=20))
]
pipe = Pipeline(estimators)
pipe.fit(X_train, y_train)
pred = pipe.predict(X_test)
accuracy_score(y_test, pred)💻 출력
0.7655502392344498
그리고 KNN으로 예측한 정확도는 76%이다.
디카프리오라는 인물의 데이터를 예상해서 위 모델에 적용시킨 생존율은 아래와 같다.
# ['pclass', 'age', 'sibsp', 'parch', 'fare', 'gender', 'grade']
# grade : ['Miss', 'Mr', 'Mrs', 'Rare_f', 'Rare_m']
dicaprio = np.array([[3,18,0,0,5,1,1]])
winslet = np.array([[1,16,1,1,100,0,3]])
print("Decaprio : ", pipe.predict_proba(dicaprio)[0,1])
print("Winslet : ", pipe.predict_proba(winslet)[0,1])💻 출력
Decaprio : 0.1
Winslet : 0.85