역전파 알고리즘 (Backpropagation)

역전파 알고리즘은 입력이 주어지면 순방향으로 계산하여 출력을 계산한 후에 실제
출력과 우리가 원하는 출력 간의 오차를 계산한다.

1. 가중치 초기화
   모든 가중치와 바이어스를 0∼1 사이의 난수(random number)로 초기화한다.

2. 반복 학습
   오차가 충분히 작아질 때까지, 모든 가중치에 대해 아래 과정을 반복한다.

3. 손실 함수의 그래디언트 계산
   각 가중치에 대해 손실 함수 $E$의 기울기(gradient) 를 계산한다:

   $\frac{\partial E}{\partial w}$

4. 가중치 업데이트
   경사하강법을 이용해 가중치를 오차를 줄이는 방향으로 업데이트한다:

   $w(t+1) = w(t) - \eta \cdot \frac{\partial E}{\partial w}$

• $\eta$: 학습률 (learning rate)

역전파를 통해 구한 기울기(gradient)를 사용하여, 손실 함수 $E(w)$ 가 최소가 되는 지점까지 학습을 진행한다.

---

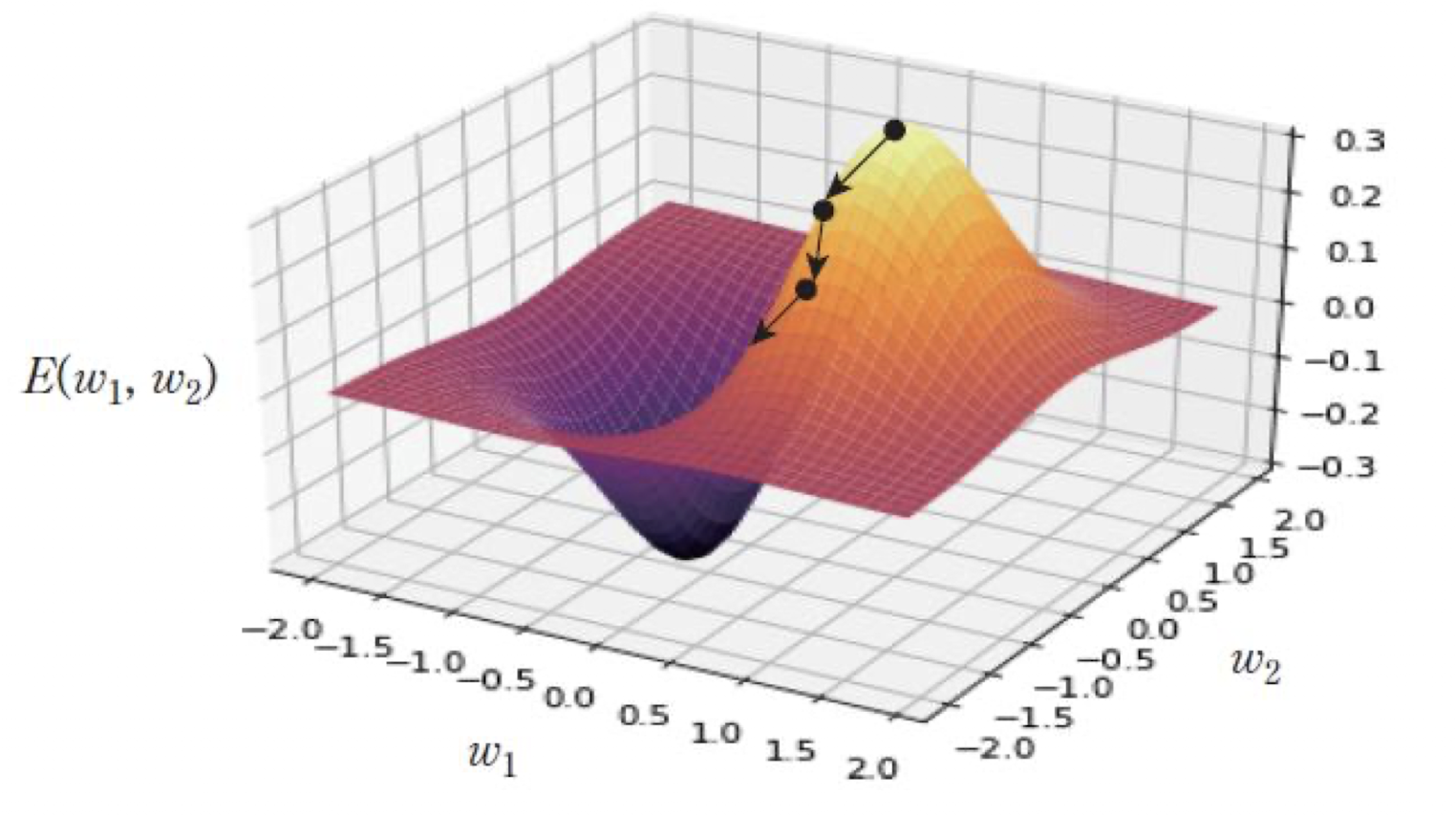
미분의 Chain Rule (연쇄 법칙)

신경망은 여러 층으로 이루어져 있으므로, 출력까지의 경로가 함수의 합성으로 되어 있음.

예를 들어,

• $y = f(u)$
• $u = g(x)$

💡 $w_1$을 변경하려면?? - $w_1$은 $h_1$ 계산에 영향을 주고 - $h_1$은 다시 $y$, 그리고 `최종 오차` $E$에 영향을 미침

단계별로 다음과 같이 나눠서 미분해 나가도록 설계:
$\frac{\partial E}{\partial w_1} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_1} \cdot \frac{\partial h_1}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1}$

---

유닛i와 유닛j를 연결하는 가중치 "유닛j가 출력층인 경우"

📌 출력층 유닛에 대한 가중치 미분: $\frac{\partial E}{\partial w_{ij}}$

Chain Rule 적용

① $\frac{\partial E}{\partial \text{out}_j}$
오차 함수가 출력값에 얼마나 민감한지

• 유닛의 출력값 변환에 따른 오차의 변화율이다.

② $\frac{\partial \text{out}_j}{\partial \text{net}_j}$
활성화 함수 $f$의 미분

• 입력합의 변화에 따른 유닛 $j$의 출력 변화율이다.
• 활성화 함수의 미분값이다.

③ $\frac{\partial \text{net}_j}{\partial w_{ij}}$
가중치 $w_{ij}$가 입력 합 $net_j$에 얼마나 영향을 주는지

• 가중치의 변화에 따른 $net_j$의 변화율이라고 할 수 있다.

✅ 최종 미분 식 정리

---

유닛i와 유닛j를 연결하는 가중치 "유닛j가 은닉층인 경우"

📌 은닉층 유닛에 대한 가중치 미분: $\frac{\partial E}{\partial w_{ij}}$

은닉 유닛의 오차는 출력처럼 직접 계산되지 않기 때문에,
출력층으로부터 역으로 전파된 오차를 바탕으로 계산해야 한다.

Chain Rule 적용 (은닉층)

①$\frac{\partial E}{\partial \text{out}_j}$: 은닉 유닛 $j$의 오차
은닉층은 직접 정답이 없기 때문에, 연결된 출력층 유닛 $k$ 들로부터 오차를 전달받음:

• $L$은 은닉 유닛 $j$ 와 연결된 출력 유닛들의 집합

이미 계산된 $\frac{\partial E}{\partial out_k}\cdot\frac{\partial out_k}{\partial net_k}$ 에 $w_jk$만 곱하면 됨
👉 앞에서 계산된 거에다가 이미 없데이트 된것을 곱하면 됨

② $\frac{\partial \text{net}_j}{\partial \text{out}_j} = f'(\text{net}_j)$

• 활성화 함수의 미분값

③ $\frac{\partial \text{net}_j}{\partial w_{ij}} = \text{out}_i$

• 앞쪽 유닛 $i$의 출력값

✅ 최종 미분 식 정리

여기서

으로 정의됨 → 이게 은닉층 오차의 핵심 공식

---

📕 역전파 알고리즘 정리 "delta"

$\delta_k$ 란?

• 유닛 $k$에서의 오차를 의미
• 출력층이나 은닉층의 유닛에서 오차의 변화를 전달하는 값

👉 출력층 유닛 $j$

👉 은닉층 유닛 $j$

즉, 신경망 레이어에 따라서 다음과 같이 구분하여서 계산한다.

그라디언트(기울기)를 계산하는 데 필요한 값!

가중치 업데이트

• 가중치 미분:
  출력층일 때는 $\delta_j$값에 입력값 $out_i$를 곱해서 계산:
  $\frac{\partial E}{\partial w_{ij}} = \delta_j \cdot out_i$
• 은닉층일 때는 델타값을 이용해 이전 층으로부터 전파된 오차를 기반으로 계산:
  $\frac{\partial E}{\partial w_{ij}} = (out_j - target_j) \cdot f'(net_j) \cdot out_i$

델타의 역할

델타 $\delta_k$는 오차를 출력층에서 은닉층으로, 은닉층에서 입력층으로 전파하는 데 중요한 역할을 한다.

신경망의 학습은 이 델타 값을 통해 오차를 각 유닛에 전파하고, 이를 반영하여 가중치를 업데이트하는 방식으로 진행된다.

---

🧮 역전파 알고리즘 직접 계산

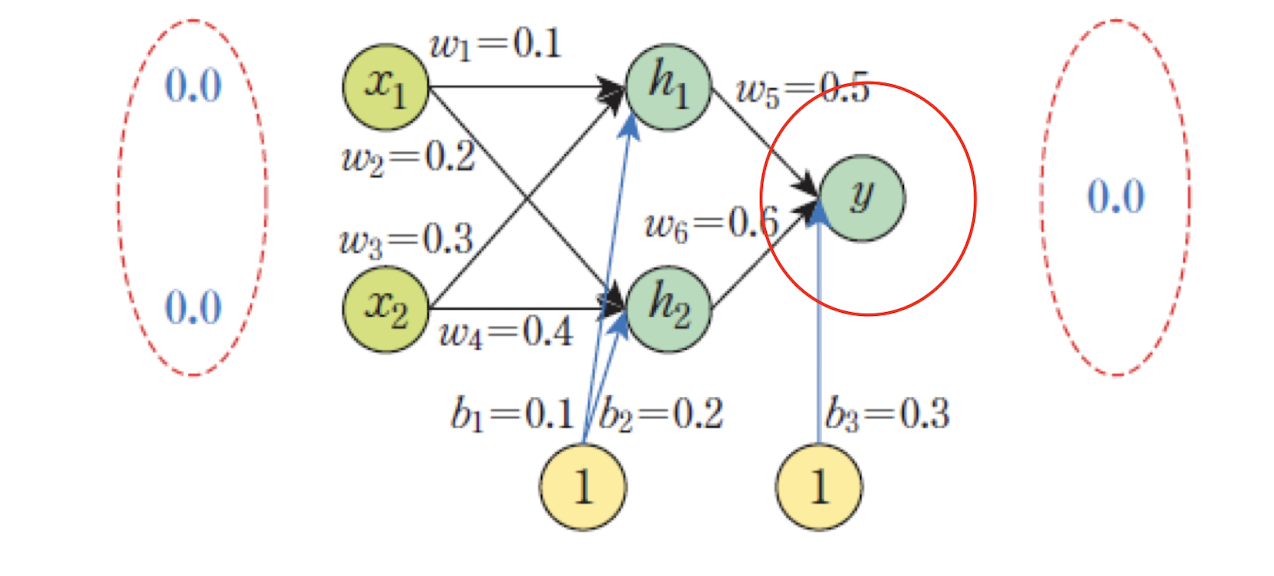
✅ 순방향 패스 (Forward Pass)

1. 출력층 유닛 $y$에 대한 출력 계산:
   가중치와 입력 값들을 계산하여 $net_y$를 구한다.

   $\text{net}_y = w_5 \cdot \text{out}_{h1} + w_6 \cdot \text{out}_{h2} + b_3$
   $= 0.5*0.524979+0.6*0.549834+0.3=0.89239$

   여기서 $out_{h1}$과 $out_{h2}$는 은닉층에서 나오는 값이다.
   이 값을 sigmoid 함수로 통과시켜 최종 출력 $out_y$를 얻는다.

   $\text{out}_y = \frac{1}{1 + e^{-\text{net}_y}} = \frac{1}{1 + e^{-0.89239}} \approx 0.709383$

2. 총 오차 계산
   목표 출력 $target_y=0.0$과 계산된 출력 $out_y$사이의 오차를 계산한다.

---

✅ 역방향 패스 (Backward Pass)

📌출력층 → 은닉층

1. 가중치 $w_5$의 변화가 출력 오차에 미치는 영향을 계산 Chain Rule
   $\frac{\partial E}{\partial w_5} = \frac{\partial E}{\partial \text{out}_y} \cdot \frac{\partial \text{out}_y}{\partial \text{net}_y} \cdot \frac{\partial \text{net}_y}{\partial w_5}$

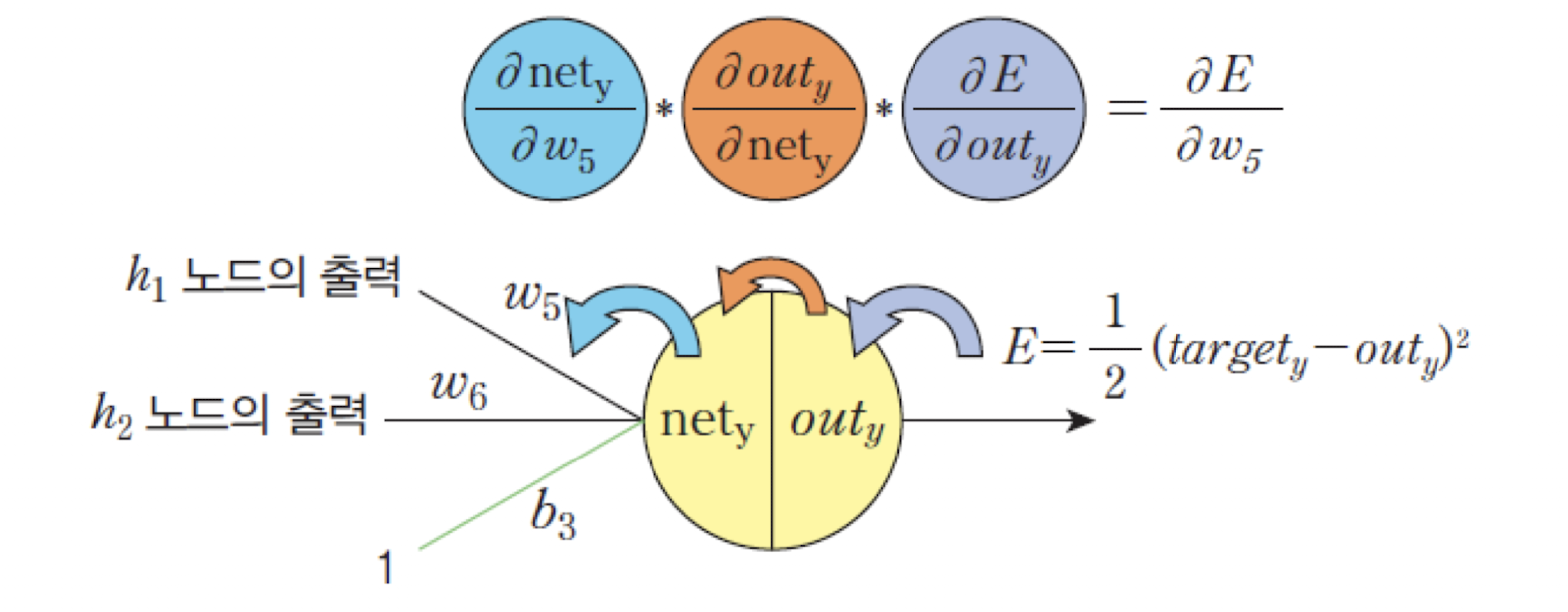
단계별로 미분:

• 출력층에 대한 오차:
  $\frac{\partial E}{\partial \text{out}_y} = (\text{out}_y - \text{target}_y) = 0.709383 - 0 = 0.709383$

layer2_error = layer2*y

• 활성화 함수 미분 (sigmoid 함수의 미분):
  $\frac{\partial \text{out}_y}{\partial \text{net}_y} = \text{out}_y \cdot (1 - \text{out}_y) = 0.709383 \cdot (1 - 0.709383) = 0.206158$

layer2_delta=layer2_error*actf_deriv(layer2)

• 가중치 미분:
  $\frac{\partial \text{net}_y}{\partial w_5} = \text{out}_{h1} = 0.524979$

---

2. 최종 기울기 계산
   따라서 $w_5$에 대한 기울기는:
   $\frac{\partial E}{\partial w_5} = \frac{\partial E}{\partial \text{out}_y} \cdot \frac{\partial \text{out}_y}{\partial \text{net}_y} \cdot \frac{\partial \text{net}_y}{\partial w_5}$
   $= 0.709383 \cdot 0.206158 \cdot 0.524979 = 0.076775$
   이 값은 경사하강법을 이용하여 가중치를 업데이트하는 데 사용된다.

layer2_delta*layer1.T

---

📌 가중치 업데이트

경사하강법을 통해 $w_5$의 값을 업데이트한다:

여기서 학습률 $η$는 0.5이고, 따라서:

역방향 패스는 출력 오차를 은닉층으로 전파하여 각 가중치가 오차에 미치는 영향을 계산한다.
이 정보를 바탕으로 가중치를 업데이트하는 과정이다.

• 가중치가 점점 낮아진다.
• 바이어스는 기존 값보다 낮아지게 된다. 이는 다음번에 유닛의 출력을 더 낮게 만들것이다.

👉 우리가 원하는 출력값은 0 이기 때문이다.

---

📌 은닉층 → 입력층

1. 가중치 $w_1$의 업데이트 계산:
   $w_1(t+1) = w_1(t) - \eta \cdot \frac{\partial E}{\partial w_1} = 0.10 - 0.2 \cdot 0.0 = 0.10$
   $w_2(t+1) = 0.2, \quad w_3(t+1)=0.3, \quad w_4(t+1)=0.4$

• 입력값이 0인 경우에는 가중치는 변화하지 않는다.
• 입력이 0이면 가중치를 아무리 바꿔도 무슨 소용이 있나?

2. 바이어스 $b_1$와 $b_2$업데이트:
   $b_1(t+1) = 0.096352, \quad b_2(t+1) = 0.195656$

• 바이어스는 기존 값보다 낮아지게 된어, 출력값을 더 낮추는 방향으로 동작한다.

---

📌 손실함수 평가

⬇️ 경사하강법 1번 적용

⬇️ 경사하강법 10000번 적용

오차가 크게 줄어든다.

---

📦 Numpy를 이용하여 MLP 구현

import numpy as np

# 시그모이드 함수
def actf(x):
    return 1 / (1 + np.exp(-x))

# 시그모이드 함수의 미분치
def actf_deriv(x):
    return x * (1 - x)

# 입력유닛의 개수, 은닉유닛의 개수, 출력유닛의 개수
inputs, hiddens, outputs = 2, 2, 1
learning_rate = 0.2

# 훈련 샘플과 정답
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
T = np.array([[1], [0], [0], [1]])

W1 = np.array([[0.10, 0.20], [0.30, 0.40]])  # 입력에서 은닉층으로 가는 가중치
W2 = np.array([[0.50], [0.60]])  # 은닉층에서 출력층으로 가는 가중치
B1 = np.array([0.1, 0.2])  # 은닉층의 바이어스
B2 = np.array([0.3])  # 출력층의 바이어스

# 순방향 전파 계산
def predict(x):
    layer0 = x  # 입력을 layer0에 대입한다.
    Z1 = np.dot(layer0, W1) + B1  # 행렬의 곱을 계산한다.
    layer1 = actf(Z1)  # 활성화 함수를 적용한다.
    Z2 = np.dot(layer1, W2) + B2  # 행렬의 곱을 계산한다.
    layer2 = actf(Z2)  # 활성화 함수를 적용한다.
    return layer0, layer1, layer2

# 역방향 전파 계산
def fit():
    global W1, W2, B1, B2  # 외부에서 정의된 변수를 변경해야 하므로 global 사용
    for i in range(90000):  # 9만번 반복한다.
        for x, y in zip(X, T):  # 학습 샘플을 하나씩 꺼낸다.
            x = np.reshape(x, (1, -1))  # 2차원 행렬로 만든다. ①
            y = np.reshape(y, (1, -1))  # 2차원 행렬로 만든다.

            # 순방향 계산
            layer0, layer1, layer2 = predict(x)

            # 오차 계산
            layer2_error = layer2 - y  # 출력층 오차
            layer2_delta = layer2_error * actf_deriv(layer2)  # 출력층 델타 계산

            # 은닉층 오차 및 델타 계산
            layer1_error = np.dot(layer2_delta, W2.T)  # 은닉층 오차 ②
            layer1_delta = layer1_error * actf_deriv(layer1)  # 은닉층 델타 계산 ③

            # 가중치 업데이트
            W2 += -learning_rate * np.dot(layer1.T, layer2_delta)  # ④
            W1 += -learning_rate * np.dot(layer0.T, layer1_delta)  # ⑤

            # 바이어스 업데이트
            B2 += -learning_rate * np.sum(layer2_delta, axis=0)  # ⑥
            B1 += -learning_rate * np.sum(layer1_delta, axis=0)  # ⑦

# 테스트 함수
def test():
    for x, y in zip(X, T):  # 학습 샘플을 하나씩 꺼낸다.
        x = np.reshape(x, (1, -1))  # 하나의 샘플을 꺼내서 2차원 행렬로 만든다.
        layer0, layer1, layer2 = predict(x)  # 순방향 계산
        print(x, y, layer2)  # 출력층의 값을 출력해본다.

# 훈련을 하고 테스트를 실행
fit()  # 학습
test()  # 테스트

[[0 0]] [1] [[0.99196032]]
[[0 1]] [0] [[0.00835708]]
[[1 0]] [0] [[0.00836107]]
[[1 1]] [1] [[0.98974873]]

---

Summary

• MLP는 입력층과 출력층 사이에 은닉층(hidden layer)을 갖는 신경망 구조이다.
• 역전파 알고리즘은 MLP를 학습시키기 위해 사용되는 핵심 방법이다.
• 역전파의 과정:
  1. 입력이 주어지면 순방향으로 계산하여 출력을 구한다.
  2. 실제 출력과 원하는 출력의 차이인 오차를 계산한다.
  3. 이 오차를 역방향으로 전파하여 가중치를 업데이트하고, 오차를 줄이는 방향으로 학습을 진행한다.