MLP의 중요 개념들

일반적으로 훈련 샘플의 개수는 아주 많다.

• 풀배치 학습 (full batch learning)
• 온라인 학습 (online learning)
• 미니배치 학습 (mini batch learning)

---

📗 풀배치 학습

풀 배치 학습은 신경망 학습에서 모든 훈련 샘플을 한 번에 처리하는 방식이다.
이 방법은 평균 그래디언트를 계산하여 가중치를 업데이트하는 방식으로 진행된다.
하지만, 많은 샘플을 한번에 처리하기 때문에 시간이 많이 걸리고 계산이 느릴 수 있다.

1. 가중치와 바이어스를 0부터 1 사이의 난수로 초기화.

2. 수렴할 때까지 모든 가중치에 대해 다음을 반복.

3. 모든 훈련 샘플을 처리하여 평균 그래디언트 $\frac{\partial E}{\partial w} = \frac{1}{N} \sum_{k=1}^{N} \frac{\partial E_k}{\partial w}$

4. 가중치 업데이트: $w(t+1) = w(t) - \eta \cdot \frac{\partial E}{\partial w}$

---

📘 온라인 학습

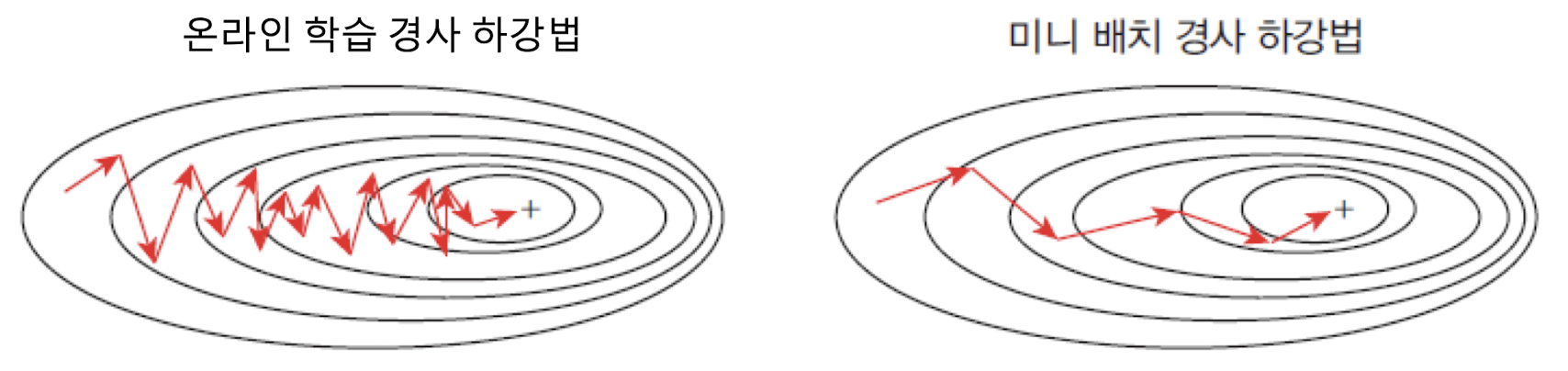
온라인 학습은 훈련 샘플 중에서 무작위로 하나의 샘플을 선택하여 가중치를 업데이트하는 방식이다.
이 방법은 계산이 쉽고 샘플마다 빠르게 학습이 가능하지만, 샘플 선택에 따라 우왕좌왕하기 쉽다.

1. 가중치와 바이어스를 0부터 1 사이의 난수로 초기화.

2. 수렴할 때까지 모든 가중치에 대해 반복.

3. 훈련 샘플 중에서 무작위로 i번째 샘플을 선택.

4. 그래디언트 계산: $\frac{\partial E}{\partial w}$

5. 가중치 업데이트: $w(t+1) = w(t) - \eta \cdot \frac{\partial E}

---

📙 미니배치 학습

미니배치 학습은 풀 배치와 온라인 학습의 중간 형태로, 훈련 샘플을 B개씩 묶어서 처리하는 방식이다.
빠르게 계산하면서도 안정적인 학습을 할 수 있다.

1. 가중치와 바이어스를 0부터 1 사이의 난수로 초기화.

2. 수렴할 때까지 반복.

3. 훈련 샘플 중에서 무작위로 B개의 샘플을 선택.

4. 그래디언트 계산: $\frac{\partial E}{\partial w} = \frac{1}{B} \sum_{k=1}^{B} \frac{\partial E_k}{\partial w}$

5. 가중치 업데이트: $w(t+1) = w(t) - \eta \cdot \frac{\partial E}{\partial w}$

📦 미니배치 실습 code

import numpy as np
import tensorflow as tf

# 데이터를 학습 데이터와 테스트 데이터로 나눈다.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
data_size = x_train.shape[0]
batch_size = 12  # 배치 크기

# 배치 크기 많큼 랜덤하게 선택
selected = np.random.choice(data_size, batch_size)
print(selected)
x_batch = x_train[selected]
y_batch = y_train[selected]

# 미니 배치 사용할 경우 MSE 함수
def MSE(t, y):
    size = y.shape[0]
    return 0.5 * np.sum((y - t) ** 2) / size

[58298 3085 27743 33570 35343 47286 18267 25804 4632 10890 44164 18822]

🖇️ 미니배치 행렬로 구현하기

XOR 연산 학습을 위한 신경망 설계:

- XOR 연산을 학습할 수 있는 신경망의 예시로, 입력층과 은닉층을 가진 네트워크가 구성된다. - 각 입력 값 $x_1, x_2$와 가중치 $w_1, w_2, w_3, w_4,$ 바이어스 $b_1, b_2$는 신경망의 연결을 나타낸다.

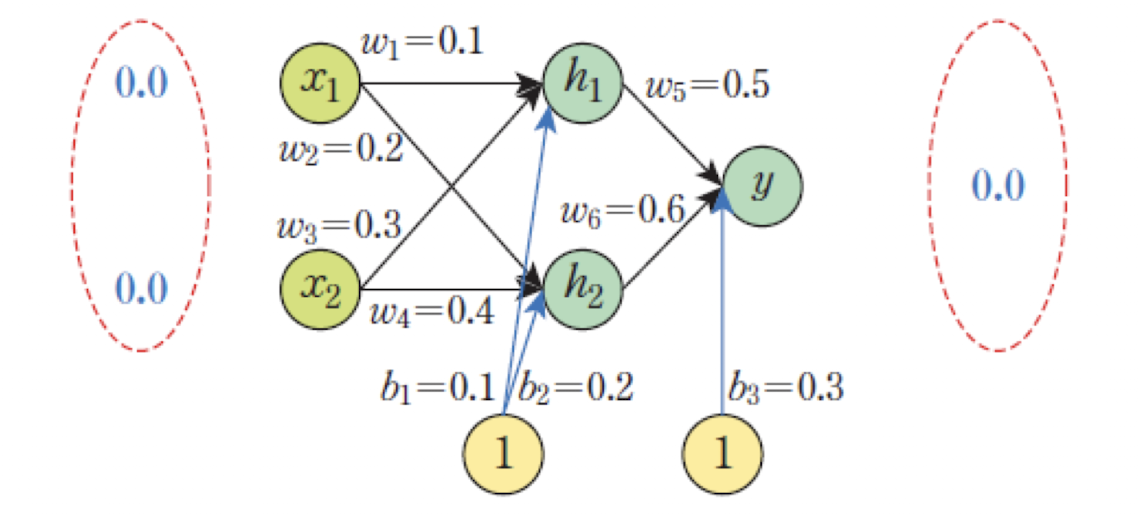
행렬계산:

• $Z_1$: 은닉층 유닛이 받은 입력의 총합을 나타내는 행렬
• $A_1$: 활성화 함수 적용 후 은닉층의 출력
• $Z_2$: 출력층 유닛이 받은 입력의 총합
• $Y$: 출력층의 활성화 함수 적용 후 최종 출력

---

• $Z_1$은 은닉층 유닛이 받는 입력의 총합을 나타내는 행렬

• $A_1$은 $Z_1$을 활성화함수에 대입한 후의 행렬

• $Z_2$는 출력층 유닛이 받는 입력의 총합을 나타내는 행렬

• $Y$는 $Z_2$에 출력층의 활성화함수를 적용하여 얻은 출력층 유닛의 출력

---

🖇️ 미니배치 오차 역전파

• Loss Function: $\quad E = \frac{1}{2} (Y - T)^T (Y - T)$
• Activation Function: $\quad Y = f(z) = \frac{1}{1 + e^{-z}}$

① $\quad \frac{\partial E}{\partial Y} = (Y - T) = \begin{bmatrix} y^{(1)} - t^{(1)} \\ y^{(2)} - t^{(2)} \\ y^{(3)} - t^{(3)} \\ y^{(4)} - t^{(4)} \end{bmatrix} \quad \text{layer2\_error}$

② $\quad \frac{\partial Y}{\partial Z_2} = Y \circ (1 - Y) = \begin{bmatrix} y^{(1)} \cdot (1 - y^{(1)}) \\ y^{(2)} \cdot (1 - y^{(2)}) \\ y^{(3)} \cdot (1 - y^{(3)}) \\ y^{(4)} \cdot (1 - y^{(4)}) \end{bmatrix} \quad \text{actf\_deriv(layer2)}$

③ $\quad \frac{\partial Z_2}{\partial W_2} = (A_1)^T = \begin{bmatrix} a_1^{(1)} & a_1^{(2)} & a_1^{(3)} & a_1^{(4)} \\ a_2^{(1)} & a_2^{(2)} & a_2^{(3)} & a_2^{(4)} \end{bmatrix} \quad \text{layer1.T}$

가중치 업데이트: $\quad w_5(t+1) = w_5(t) - \eta \cdot \frac{\partial E}{\partial w_5}$

샘플이 4개 이므로 4로 나누어서 평균 gradient를 계산하고 여기에 학습률을 곱하여 $w_5$를 업데이트한다.

---

📦 미니배치의 구현

import numpy as np

# 시그모이드 함수
def actf(x):
    return 1 / (1 + np.exp(-x))

# 시그모이드 함수의 미분치
def actf_deriv(x):
    return x * (1 - x)

# 입력유닛, 은닉유닛 및 출력유닛의 개수
inputs, hiddens, outputs = 2, 2, 1
learning_rate = 0.5

# 훈련 입력과 출력
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
T = np.array([[0], [1], [1], [0]])

# 가중치를 –1.0에서 1.0 사이의 난수로 초기화한다.
W1 = 2 * np.random.random((inputs, hiddens)) - 1
W2 = 2 * np.random.random((hiddens, outputs)) - 1
B1 = np.zeros(hiddens)
B2 = np.zeros(outputs)

# 순방향 전파 계산
def predict(x):
    layer0 = x  # 입력을 layer0에 대입한다.
    Z1 = np.dot(layer0, W1) + B1  # 행렬의 곱을 계산한다.
    layer1 = actf(Z1)  # 활성화 함수를 적용한다.
    Z2 = np.dot(layer1, W2) + B2  # 행렬의 곱을 계산한다.
    layer2 = actf(Z2)  # 활성화 함수를 적용한다.
    return layer0, layer1, layer2

# 역방향 전파 계산
def fit():
    global W1, W2, B1, B2
    for i in range(60000):
        layer0, layer1, layer2 = predict(X)
        layer2_error = layer2 - T
        layer2_delta = layer2_error * actf_deriv(layer2)
        layer1_error = np.dot(layer2_delta, W2.T)
        layer1_delta = layer1_error * actf_deriv(layer1)

        W2 += -learning_rate * np.dot(layer1.T, layer2_delta) / 4.0
        W1 += -learning_rate * np.dot(layer0.T, layer1_delta) / 4.0
        B2 += -learning_rate * np.sum(layer2_delta, axis=0) / 4.0
        B1 += -learning_rate * np.sum(layer1_delta, axis=0) / 4.0

# 테스트 함수
def test():
    for x, y in zip(X, T):
        x = np.reshape(x, (1, -1))  # 하나여도 2차원 형태이어야 한다.
        layer0, layer1, layer2 = predict(x)
        print(x, y, layer2)

# 학습 및 테스트 실행
fit()
test()

[[0 0]] [0] [[0.0124954]]
[[0 1]] [1] [[0.98683933]]
[[1 0]] [1] [[0.9869228]]
[[1 1]] [0] [[0.01616628]]

---

🏫 학습률

learning rate

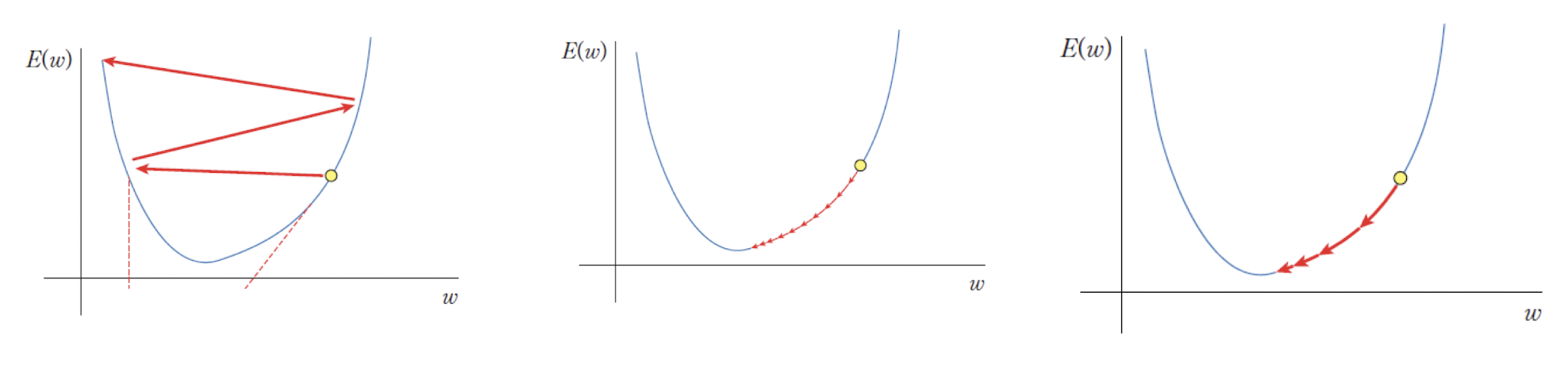
• 학습률은 신경망 학습에서 가중치를 얼마나 크게 변경할지 결정하는 값이다.

• 너무 큰 학습률은 오버슈팅을 발생시켜 최적점을 지나치게 될 수 있다.

• 너무 작은 학습률은 학습 속도가 느려지며, 지역 최소값에 빠질 위험이 있다.

• 적절한 학습률을 설정하면 최적화 과정이 원활하게 진행된다.

momentum

• 모멘텀은 이전 가중치 변화량을 반영하여 가속도를 추가하는 방법이다.

• 이 방법을 통해 가중치가 지역 최솟값을 벗어나 전역 최솟값을 찾는 데 도움이 된다.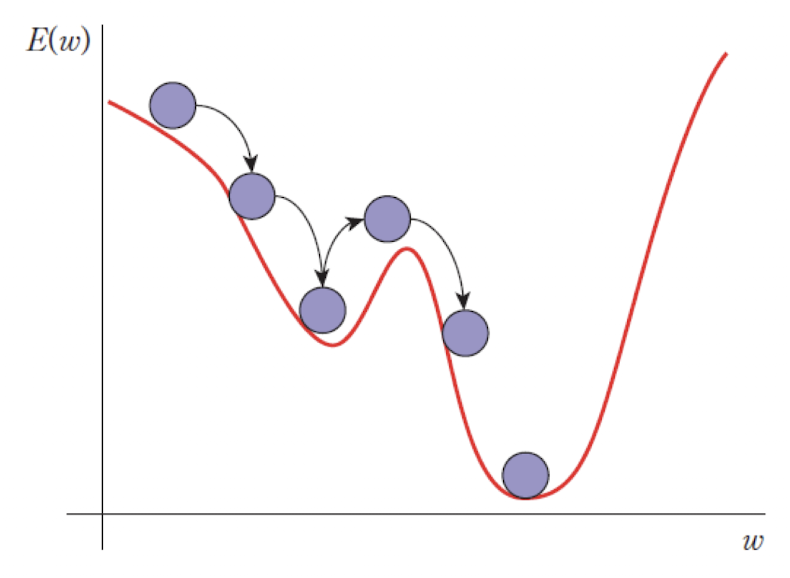

  $W_{t+1} = W_t - \eta \cdot \frac{\partial E}{\partial W} + momentum^*W_t$

  

---

Adagrad

• 가변 학습률을 사용하는 방법으로 SGD 방법을 개량한 최적화 방법이다.
• 주된 방법은 학습률 감쇠(learning rate decay)이다.
• Adagrad는 학습률을 이전 단계의 기울기들을 누적한 값에 반비례하여서 설정한다.

RMSprop

• Adagrad에 대한 수정판
• Adadelta와 유사하지만 그래디언트 누적 대신에 지수 가중 이동 평균을 사용한다.
  $W_{t+1} = W_t - \eta \cdot \frac{1}{\sqrt{v_t+\epsilon}}\frac{\partial E}{\partial W}$

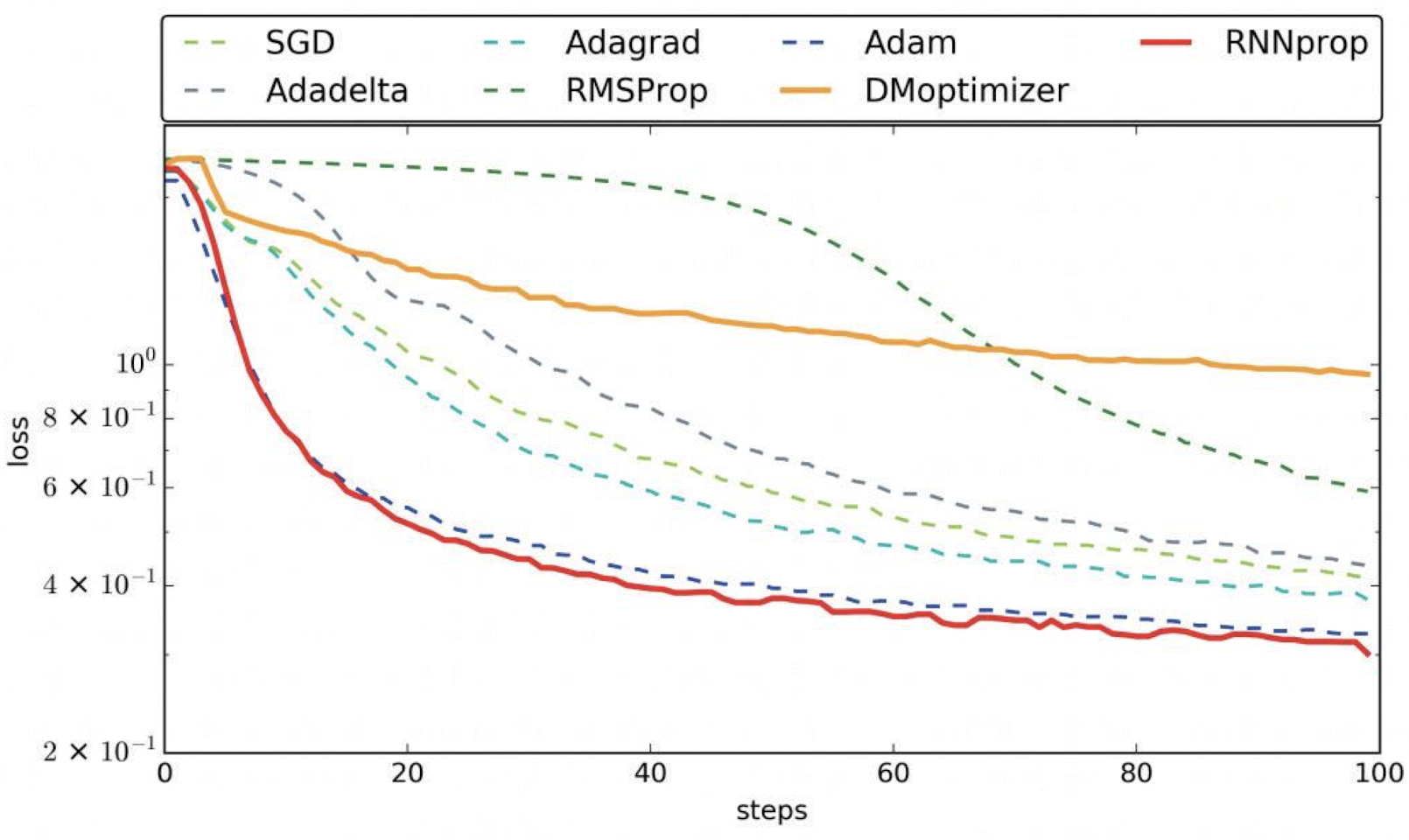
Adam

• Adaptive Moment Estimation의 약자이다.
• Adam은 기본적으로 (RMSprop+모멘텀)이다.
  현재 가장 인기 있는 최적화 알고리즘 중에 하나이다.

---

🏷️ Summary

학습 방법과 학습률

• 풀 배치는 전체 데이터를 처리한 후 가중치를 업데이트하며 안정적이지만 느리다.

• SGD는 하나의 샘플만 보고 업데이트하므로 빠르지만 불안정하다.

• 미니 배치는 그 중간으로, 여러 샘플을 묶어 균형 잡힌 학습을 진행한다.

• 학습률은 핵심 하이퍼파라미터이며, RMSprop, Adam과 같은 알고리즘은 적응적으로 학습률을 조정한다.