강의 보기

목차

1. System of equations
2. Inverse matrices
3. Rank
4. Column space
5. Null space

System of equations(선형 방정식계, 선형계)

방정식계란 미지수인 변수 리스트와 변수들과 관련된 방정식의 리스트를 가진 경우를 말합니다.

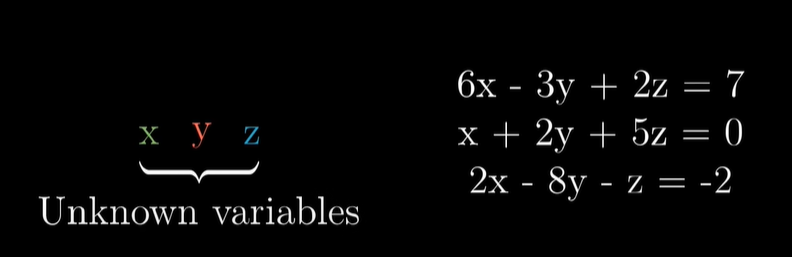
각 방정식 내에서 각 변수들의 역할은 어떤 상수를 스케일링하는 것이다. 스케일된 변수들을 서로 더하는 것이 전부입니다. 이런 변수를 조직화 한 것이 일종의 특수한 방정식계라 볼 수 있습니다.

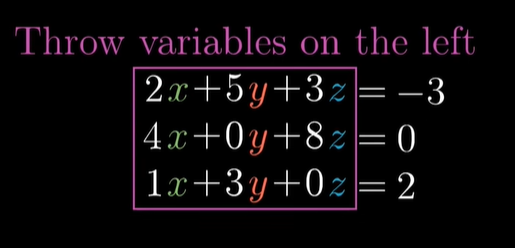
모든 변수들을 좌항으로 던지고,

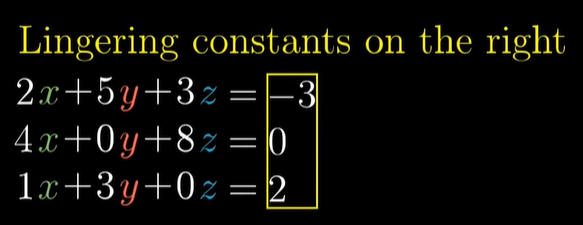
오른쪽에는 상수를 놓습니다.

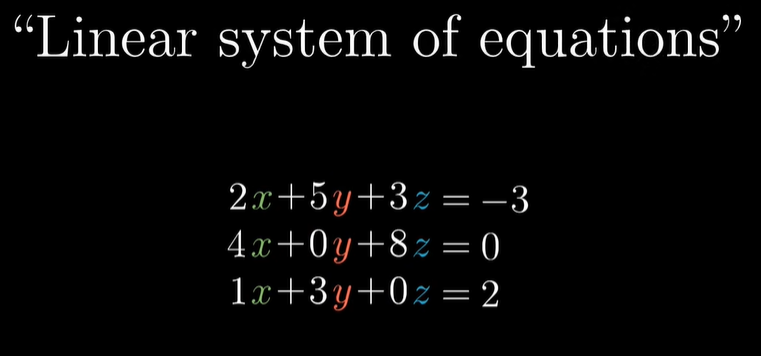
이렇게 놓은 것을 "Linear system of equations, 선형 방정식계"라고 합니다.

여기서 행렬-벡터 곱셈이랑 많이 비슷해 보인다는 걸 눈치채셨나요? 위의 모든 방정식은 하나의 벡터 방정식으로 표현할 수 있습니다.

상수 계수만을 모아서 Coefficients를 만들고, 변수만 모아서 벡터를 만들어서 행렬 벡터 곱셈하면 다른 상수 벡터와 같아집니다.

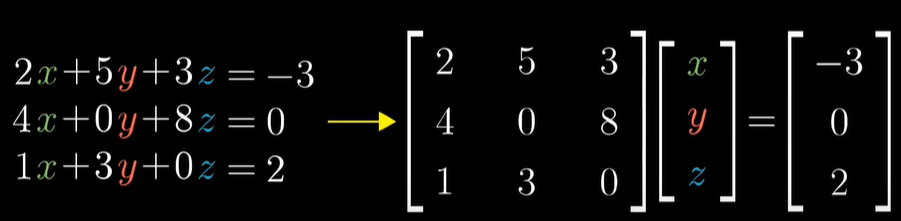
왼쪽의 행렬을 상수 행렬을 A, 변수는 벡터 v라고 표현한다면, 하나의 벡터가 만들어졌네요.

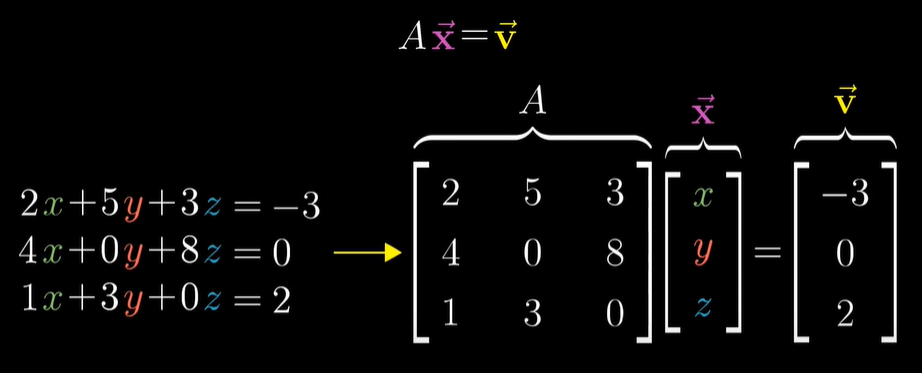
이것이 바로 선형방정식계를 짧게 표현한 것입니다.

이제 이 방정식의 해를 찾는 방법은 무엇이 있을까요?

행렬 A 변환이 모든 공간을 더 낮은 차원으로 축소 시키는 지, 선이나 점 같은 공간으로 변환 시키는지, 아니면 공간 전부가 그대로 남는 지 등을 알아보는 것이 시작점입니다!

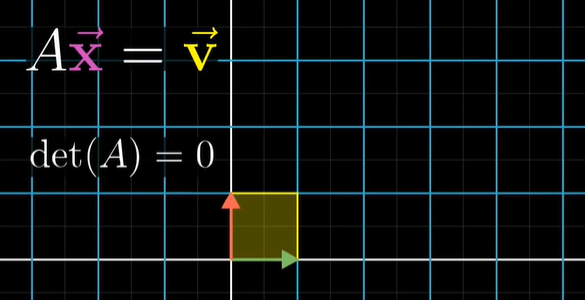
이는 지난 강의에서 다룬 행렬 A의 행렬식 값이 0인지 아닌지를 보는 것과 같습니다.

det(A) != 0 의 경우는?

공간을 제로 영역으로 축소시키지 않는 경우

Inverse matrices | 역행렬

역행렬이 등장합니다. 역의 방향으로 전환한 경우를 뜻하는데요. 이를 역변환이라고도 합니다.

위는 행렬 A의 역행렬 예시를 보여주고 있습니다. 중요한 건 이 영상에서는 계산을 가르쳐 주지 않습니다! 개념만 이해하고 넘어갑시다.

다시 원래의 행렬 A에 A의 역행렬을 곱해줍니다. 일반적으로 이것은 다시 시작한 점으로 돌아온다고 설명하고 있습니다. 아무 것도 바꾸지 않은 행렬과 같다는 의미입니다. 이게 무슨 말일까요?

아무 것도 하지 않는 변환을 "항등 변환(identity transformation)"이라고 하는데요.

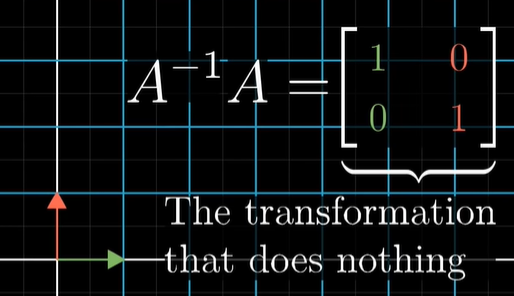
원래의 모습 그대로 둔다. i-hat, j-hat의 그대로 모습을 두기 때문에 (1,0),(0,1)이 되는 것입니다. 위의 그림을 보면 더 잘 이해가 될 것입니다!

방정식을 푸는 방식도 이렇게 생각할 수 있습니다.

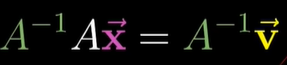
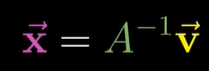
이해가 되시나요?

A의 역행렬과 A를 곱하면 '아무 변환도 일어나지 않는다' 이기 때문에 원래의 방정식만 남고 옆에 역행렬과 벡터를 곱한 값을 구하면 방정식의 답을 구할 수 있게 되는 것이죠!

아까 앞에서 det(A) != 0 의 경우를 간단히 짚고 넘어갔었죠. 공간을 제로 영역으로 축소시키지 않는다고 설명을 하고 넘어갔었는데요. 이건 역행렬의 중요한 속성에 속합니다.

det(A) != 0일 경우에만 역행렬이 존재하기 때문입니다!

det(A) = 0 의 경우는?

반대로 더 작은 차원으로 축소 시키는 것이기 때문에 역행렬은 존재하지 않습니다.

즉, 역행렬이 존재하기 위해서는 아무 것도 하지 않는 변환, "항등 변환(identity transformation)"이 성립해야 되겠네요.

Rank | 랭크

공간을 하나의 선으로 수축하는 경우가 공간을 평면으로 수축하는 경우도 있습니다. 이 경우는 단순히 "행렬식 0(zero determinant)"보다 더 정확한 표현이 필요할 것 같습니다.

변환의 결과가 1이라면(=즉, 선이라면, 1차원이라면), 이 경우를 랭크(rank)=1이라고 합니다.

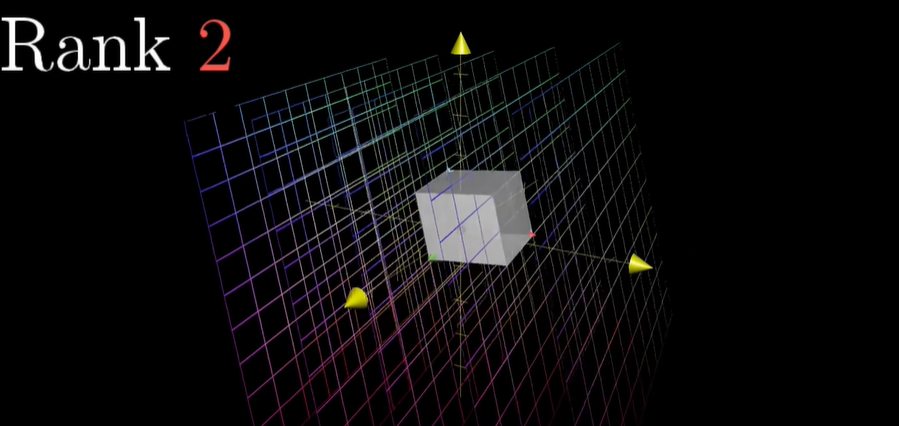
변환의 결과가 2라면 이 경우는 RANK = 2입니다.

그래서 랭크의 의미는 Number of dimensions in the output

RANK는 변환 결과의 차원수를 의미합니다.

Q1. 예를 들어, 2x2 행렬의 경우에 최대로 될 수 있는 rank는 몇일까요?

바로 2 입니다. 기저 벡터를 확장 시켜서 온전한 2차원 공간을 만들 수 있습니다. 행렬식 값이 0이 아니기도 합니다.

Q2. 그렇다면 3x3에서 rank가 2이라는 말은 무엇을 뜻하나요?

이것은 3차원에서 2차원으로 공간이 축소되었음을 뜻합니다.

3차원 변환의 행렬식 값이 0이 아니고, 3차원 공간의 결과가 온전한 3차원이라면 이때 RANK = 3이라고 말 할 수 있겠습니다.

Column space | 열공간

행렬의 가능한 열 집합을 그 행렬의 "열 공간(Column space)"이라고 합니다.

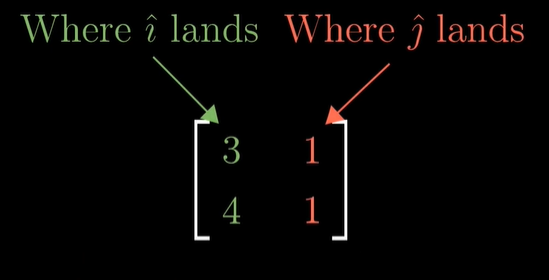
'행렬의 열들은 기저벡터의 변환 후 위치'라는 것이 이해가 되신다면, 변환 후 기저벡터들의 확장 공간은 가능한 모든 결과 공간을 알려준다는 것이 이해가 되실 겁니다.

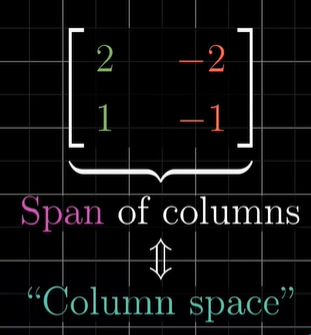
즉, 열 공간(column space)란 행렬의 열들의 확장 공간입니다.

그렇다면 여기서 랭크를 다시 더 정확하게 재정의 할 수 있습니다.

랭크(Rank)는 열공간의 차원 수입니다.

Q3. 랭크가 높아진다는 건 무엇을 의미하나요?

랭크는 열의 갯수와 같다는 말이고, 열의 갯수가 많아짐을 의미합니다.

그리고 랭크와 열의 갯수가 같은 상태를 "온전한 랭크(full rank)"라고 부릅니다.

여기서 기억해야 할 점은 영 벡터(zero vector)는 어느 열공간에든지 포함되어 있다는 점입니다!

선형 변환은 반드시 원점이 고정되어 있어야 하기 때문입니다. 이게 이해가 안 되신다면 Linear transformation 챕터를 복습하고 오셔야 합니다.😁

완전한 랭크(full rank)인 변환에서 원점으로 변하는 벡터는 영벡터 뿐입니다.

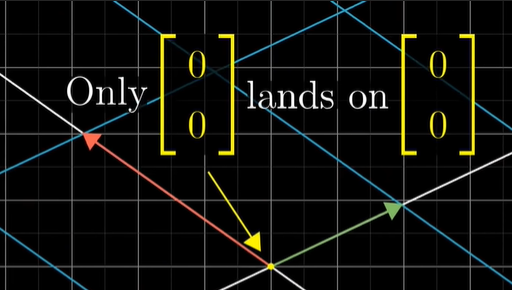
Q4. full rank가 아니라는 말은 무슨 뜻인가요?

차원이 축소되거나 확장된다는 것을 의미합니다!

만약 행렬이 full rank가 아니라면, 더 작은 차원으로 축소되는 경우라면, 제로 벡터가 되는 수많은 점을 가지게 됩니다.

Null space | 영공간

3차원 변환이 공간을 선으로 축소시킨다면, 한 평면의 모든 벡터들이 원점으로 이동하게 됩니다.

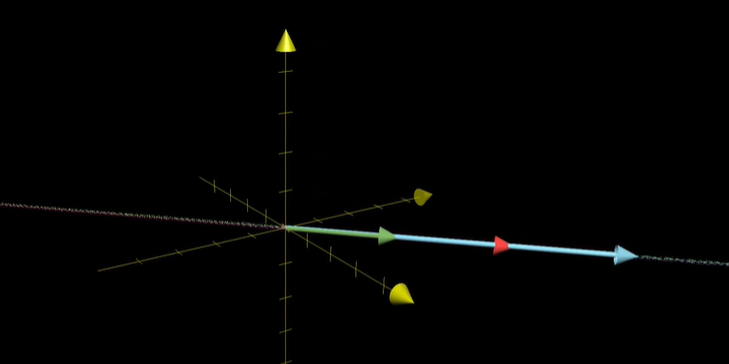
이 그림처럼요.

원점으로 이동되는 벡터들의 집합을 그 행렬의 "영공간(Null Space)" 혹은 "커널(kernel)"이라고 부릅니다.

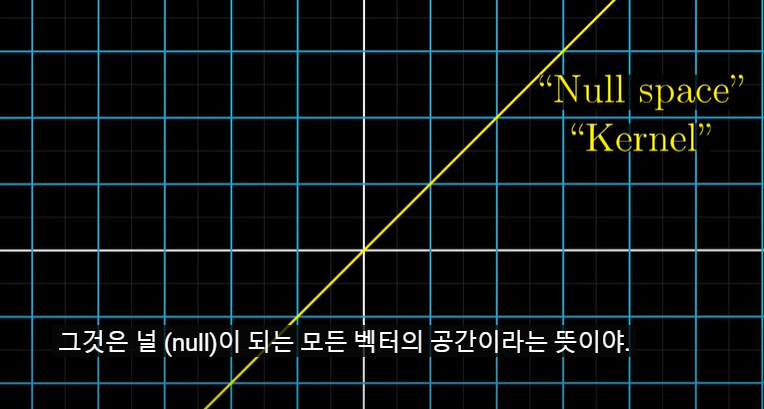
영공간, 커널은 널(Null)이 되는 모든 벡터의 공간이라는 뜻입니다. 벡터들이 모두 영벡터로 이동하는 것입니다.

선형 방정식계 용어로 말하면,

벡터 v가 영벡터인 경우, 영공간(null space) 모두가 해가 될 수 있습니다.