강의 바로 보러가기: 클릭
Review Ch.9
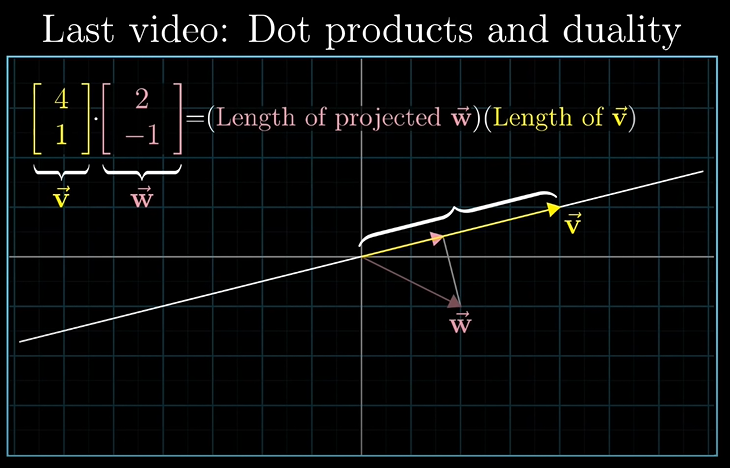
지난 강의에서는 내적(dot product)과 선형 변환에 대해 배웠습니다.
이번 강의에서는 외적(cross product)에 대해 설명할 예정입니다.
벡터 v, w의 외적
벡터 v, w의 외적은 x 기호를 사용하여 v X w 라고 적고, 평행사변형의 면적(area)를 뜻합니다.
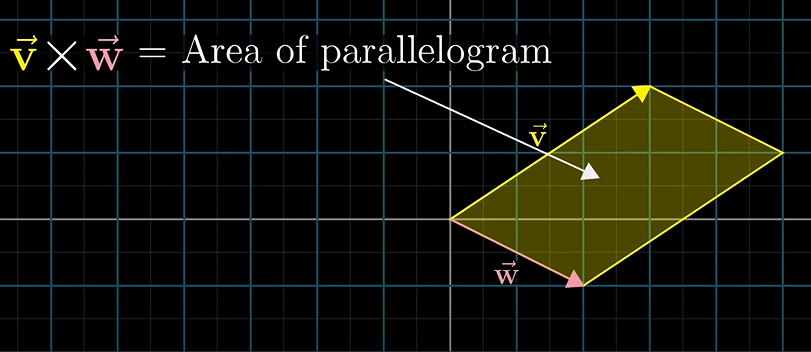
여기서 이제 방향을 고려해주면 되는데요.
기본적으로 벡터v가 벡터w의 오른쪽에 있는 경우 두 벡터의 곱, vXw 값은 양수(positive)이고 평행사변형의 면적과 동일하고
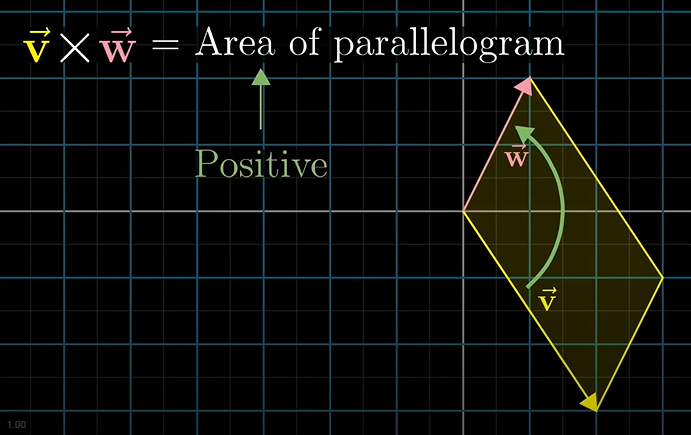
벡터v가 벡터w의 왼쪽에 존재하는 경우, 외적(cross product)는 음수(negative)가 됩니다. 말그대로 평행사변형 면적의 음수값이 됩니다.

Prerequisite: Understanding determinants
전제조건: 행렬식(determinants)에 대한 이해

행렬식은 변환에 의해 면적(area)이 얼마나 변하는지 측정하는 게 전부입니다.
2차원 행렬을 떠올리고, 변환 전 영역을 보면
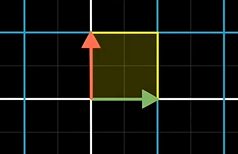
i-hat과 j-hat은 정사각형(unit square)을 이루고 있고, 변환 후에는 평행사변형이 됩니다.
그래서 행렬식이 면적 변화 요소(factor)을 구하면 그대로 이 평행사변형의 면적이 됩니다.
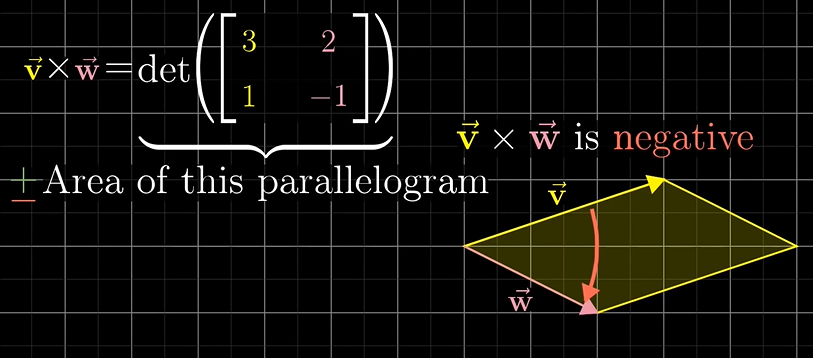
여기서 방향(orientation)이 변환에 의해 뒤집혔으면 음수값을 갖게 됩니다.
More perpendicular
두 벡터가 수직에 가까운 상태일 때, 외적은 두 벡터가 같은 쪽으로 기울어져 있는 겨우보다 큽니다.
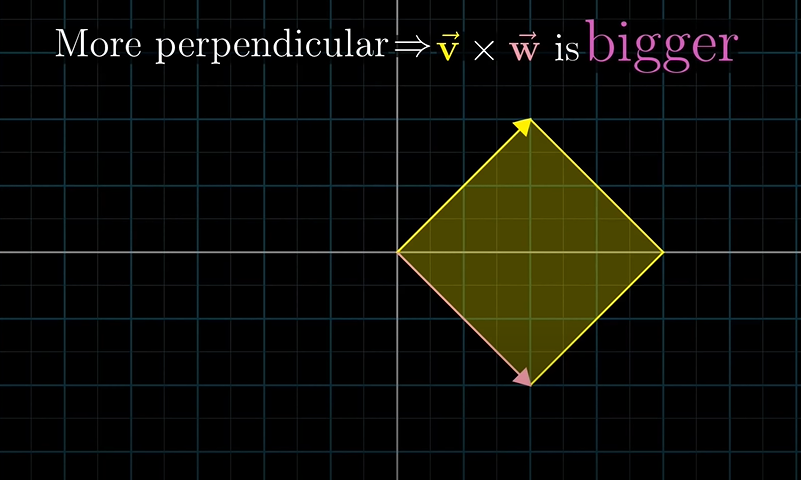
그 이유는 단순히 평행사변형의 면적은 수직에 가까울 수록 최댓값이 되기 때문이다.

Area of parallelogram
Area of parallelogram 평행사변형의 면적은 중요합니다.
위의 정리를 통해 잊지 말아야 할 것은
외적의 결과는 숫자가 아니라 벡터이다.
라는 점입니다.
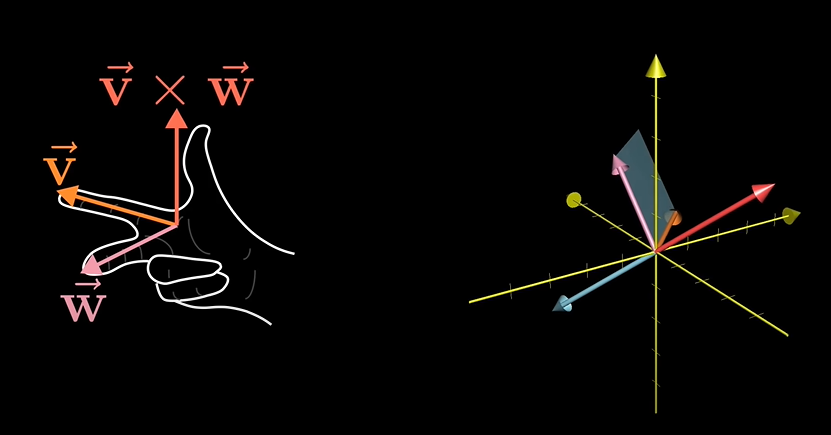
3차원에서는 새 벡터의 길이가 바로 평행사변형의 면적과 같습니다.

평행사변형에 수직한 방향입니다. 여기서는 오른쪽 손의 법칙을 설명하는데 엄지 손가락이 가리키는 방향이 외적의 방향이 됩니다.
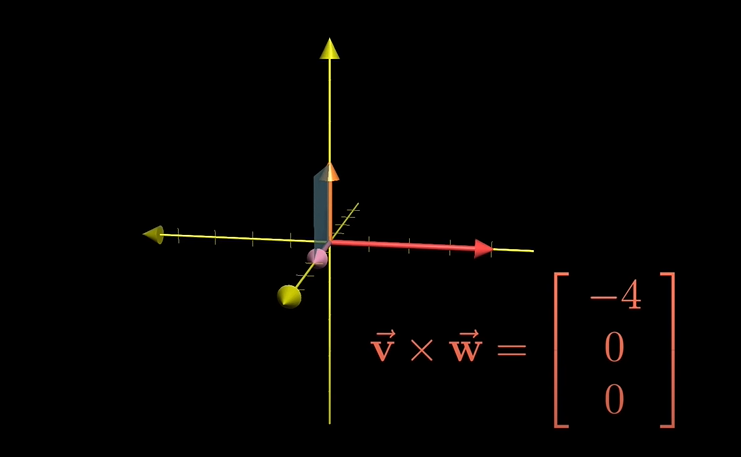
위의 예는 정사각형의 면적이 4인 경우(Area = 4)이고 결과적으로 이 두 벡터의 외적은 -4*i가 됩니다.
3차원 행렬식
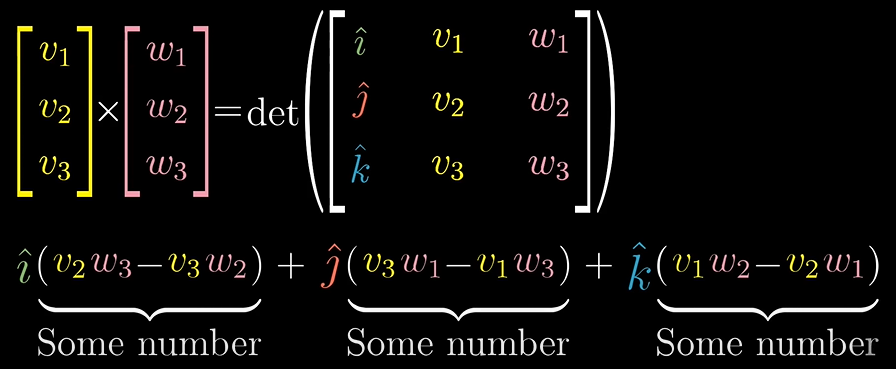
먼저 3차원 행렬을 만듭니다.
두 번째, 세 번째 열을 v, w 벡터로 채우고, 첫 번째 열은 기저벡터 i-hat, j-hat, k-hat을 적습니다. 그리고 나서 행렬식을 계산합니다.
그렇다면 기저벡터들의 선형 조합식을 얻게 됩니다.
선형조합식은 위의 이미지처럼 계산됩니다. 선형조합식으로 계산된 벡터는 v, w 벡터에 수직한 유일한 벡터이며, 평행사변형 면적과 같습니다.
여기까지 내적과 외적에 대한 개념을 시각적으로 설명을 잘 해주었습니다! 다음 강의는 선형 변환에 따른 외적에 대해 상세히 다루는 영상이라고 합니다!
