강의 바로 보러 가기 클릭
Chapter 9| Dot products and duality
보통 내적의 개념은 선형대수학에서 벡터를 배우고 난 바로 뒤에 위치해 있습니다. 하지만 이 강의에서는 챕터 9에서야 내적에 대한 개념을 보여주고 있습니다. 내적에 대한 이해가 뒤에서 하는 것이 더 쉽다고 하는데요! 내적이 무엇인지 알아보러 갑시다!
내적(Dot products)
Dot product을 구한다는 것은 같은 좌표값으로 짝을 지어 모두 곱하고 더하는 것을 말합니다.
두 벡터 v, w의 dot product을 살펴보겠습니다.
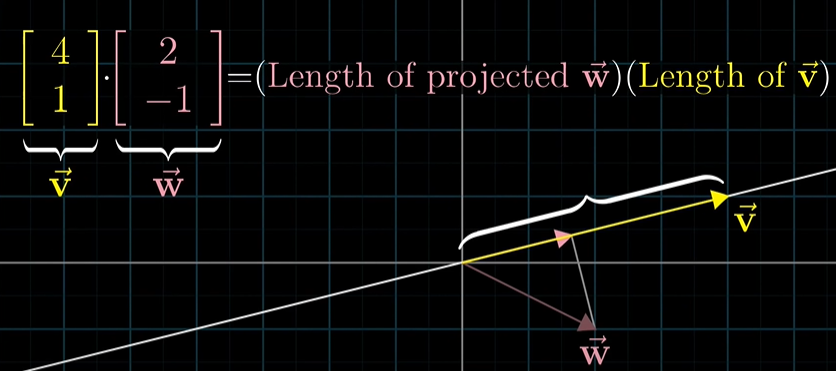
벡터 w를 원점에서 시작하고 벡터 v 위를 지나게 투영시키면,
이 투영된 w 벡터의 길이에 벡터 v 길이를 곱하는 것을 v*w 내적이라고 합니다.
만약 w 벡터 투사체가 v 벡터 방향과 반대라면 dot product은 음수가 됩니다.
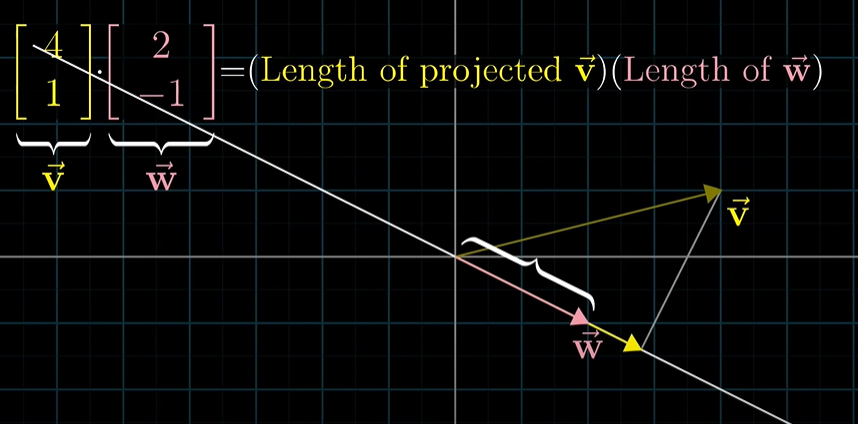
반대로 v 벡터를 w에 투영시켜도 내적은 같은 값이 나옵니다. 두 방법이 전혀 다른 계산 같지만 내적은 순서가 중요하지 않습니다!
이제 여기서 한 가지 궁금점이 들겁니다! 안 들었다고 해도 영상에서 알아서 궁금하게 만듭니다.🤗
여기서 좌표값을 매칭하고 곱하는 것과 투사(projection, 투영)과는 무슨 관계인 걸까요? 이걸 설명하기 위해 다음 개념이 필요합니다! 바로 duality!
이중성(duality)
이론은 이렇습니다. 이 영상에서는 공식 대신에 시각적으로 이해를 도와주고 있습니다!
앞서 정의했듯이 선형변환은 i-hat, j-hat의 위치에 따라 결정이 됩니다.
1차원으로 변형한 기저벡터의 도착지가 수선의 숫자로 보일 뿐이지, 결국은 행렬의 열이기 때문에 각 열들은 하나의 숫자로만 이루어지게 됩니다.

이 형태가 바로 1x2 행렬입니다.
변환을 벡터에 적용한다는 것은 무슨 의미일까요?
어떤 선형 변환이 있고 i-hat과 j-hat은 1, -2입니다.
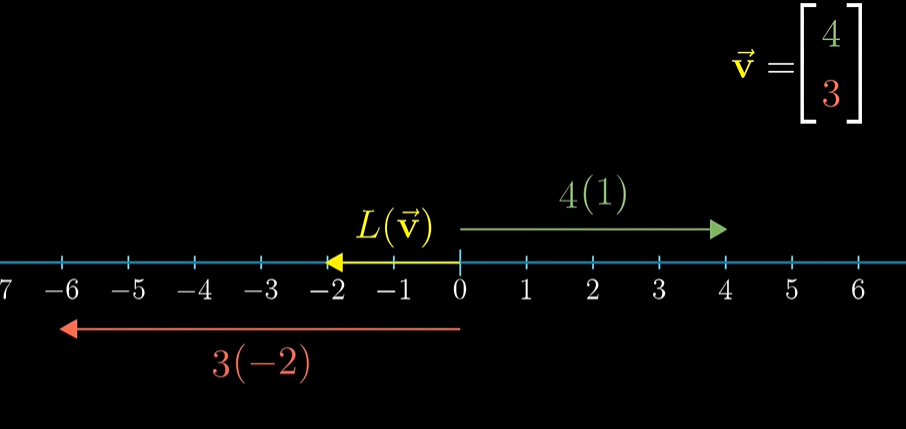
벡터 [4, 3]이 있다면 i-hat4 + j-hat3 으로 생각해야 합니다. 선형성(linearity)에 따르면 같은 비율이어야 하기 때문에 i-hat4 + j-hat3 이런 값이 되는 겁니다. 결과적으로는
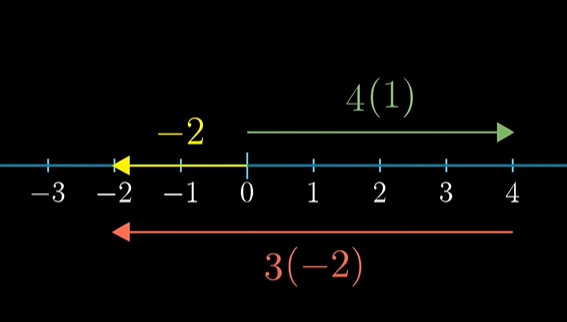
-2에 도착합니다. 이 계산은 순전히 수치적으로 보자면 행렬-벡터 곱셈이 됩니다.
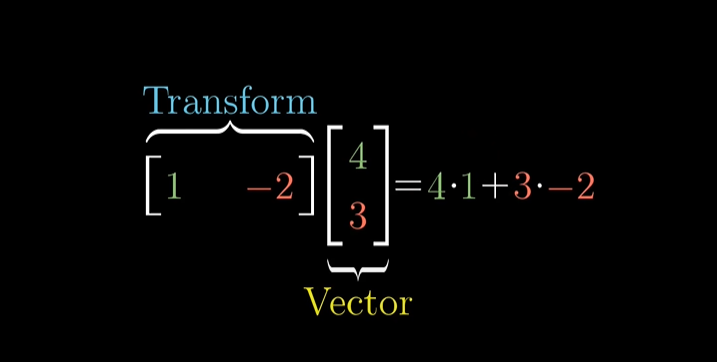
이제 이 행렬-벡터의 곱이 두 벡터의 내적과 똑같이 느껴질 것입니다.
여기서는 1x2 행렬과 2차원 벡터 사이에는 관련성이 있다고 하는데요!
입력이 벡터고 출력이 숫자인 선형변환과 벡터 그 자신과의 관계에는 연관성이 있다고 합니다.
Line of symmetry
대칭성이 있다.
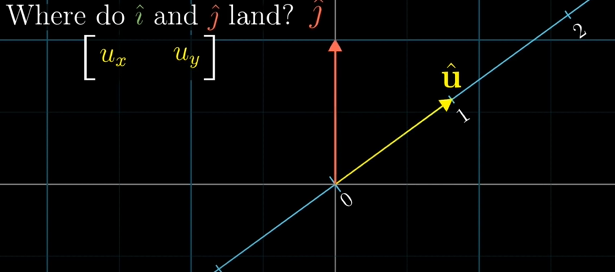
i-hat, u-hat 모두 단위벡터(길이 1)이어서 i-hat을 u-hat을 통과하는 선으로 투영하는 것은 u-hat을 x축(i-hat)에 투영하는 것과 완전히 대칭입니다.
그래서 i-hat이 투영 위치를 구할 때 u-hat을 x축에 투영된 위치를 구하는 것과 똑같습니다.
그런데 u-hat을 x축에 투영하는 것은 u-hat의 x 좌표값을 구하는 것과 같습니다.
같은 이유로 u-hat의 y 좌표값은 j-hat을 수선으로 투영한 위치와 같습니다.
투영 변환을 나타내는 1x2 행렬은 그냥 u-hat의 좌표가 됩니다!
임의 벡터 투영은 이 행렬에 임의 벡터를 곱하는 것이고, 이건 계산적으로 u-hat과의 내적(dot product)과 똑같습니다.
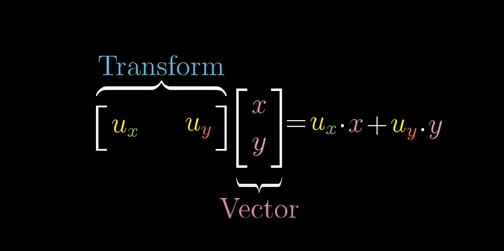
이것이 단위벡터의 내적과 벡터를 단위벡터로 투영한 길이를 구하는 것과 같은지 설명해줍니다.

이제 여기서 배울 것은 선형 변환 중 하나를 가지고 있다면,
즉, 결과 공간이 수선(number line)인 선형변환을 가지고 있다면, 어떻게 정의하든지 간에 어떤 유일한 벡터가 그 변환에 대응되고 있습니다.
이것이 수학에서 말하는 "이중성(duality)"에 관한 경우입니다!

자연스러우면서 놀라운 대응관계가 두 개의 수학적 대상물 사이에서 나타나는 것이라 설명하고 있습니다.
벡터에서 "이중(dual)"이라는 것은 그 벡터가 가진 선형변환 성질을 말합니다.
그리고 1차원에서 변환시키는 선형변환에서 이중(dual)이란, 공간상의 특정 벡터를 말합니다.

내적은 벡터가 같은 방향을 가리키는지 알아내는데도 유용한 도구이며, 두 벡터를 내적하는 것(dotting)은 두 벡터 중 하나를 변환인자로 보는 것입니다.
다음 영상에서는 이중성에 대한 예제와 외적에 대해 설명할 것이라고 합니다!
