Chapter8 강의 보기
이번 강의는 이때까지 배웠던 행렬식(determinant)과는 다른 형태를 배우게 될 것입니다. 왜냐하면 이때까지 2x2, 3x3 같은 n차 정방 행렬만 보았기 때문입니다!
그래서 저희는 선형변환도 2→2차원, 3→3차원의 변형만 다루었죠.
오늘은 3x2 matrix😱를 배우게 될 거예요!

이제 여기선 i-hat과 j-hat이 눈에 잘 보이겠죠!
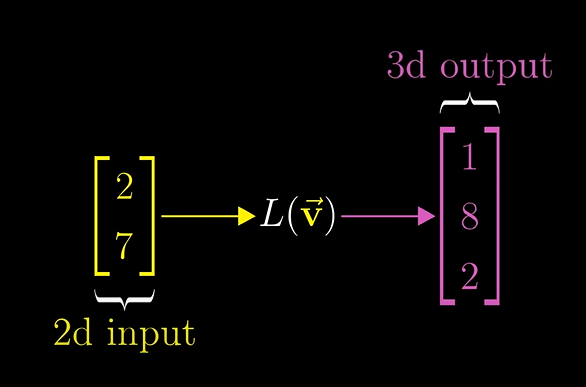
이젠 2차원 벡터를 3차원 벡터로 변환하는 과정을 살펴보겠습니다.
선형(Linear)이란?
격자선이 평행하고 균등 간격을 가지며, 원점은 계속 원점인 경우
3x2 matrix

여기선 (1,0)에서 i-hat은 (2,-1,-2)가 되고, (0,1)에서 j-hat은 (0,1,1)이 됩니다.
주목할 점은 3x2 matrix라는 점입니다. 행렬의 열공간은 3차원 공간의 원점을 가로지르는 2차원 평면상의 모든 벡터가 됩니다.

하지만 행렬은 여전히 full rank입니다. 이 열공간의 차원수가 입력공간의 차원수와 같기 때문입니다.
두 열이 입력공간의 두 기저벡터를 말하는 거라서 기저벡터의 도착지인 각 열의 3개의 행은 3개의 다른 좌표값을 나타냅니다.
2x3 matrix
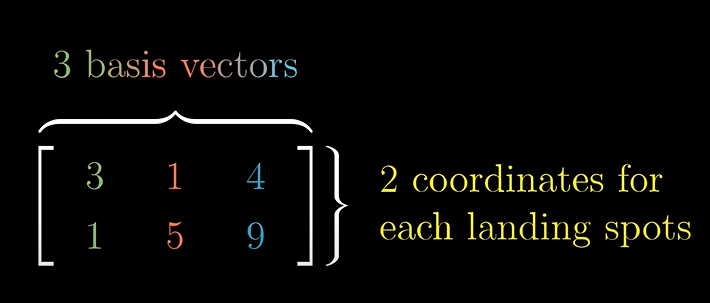
- 3개의 열은 3개의 기저벡터를 가진 공간에서 시작했다는 뜻으로 3차원에서 시작했다는 뜻입니다.
- 2개의 행이 의미하는 것은 세 기저벡터의 변환 후를 말해줍니다.
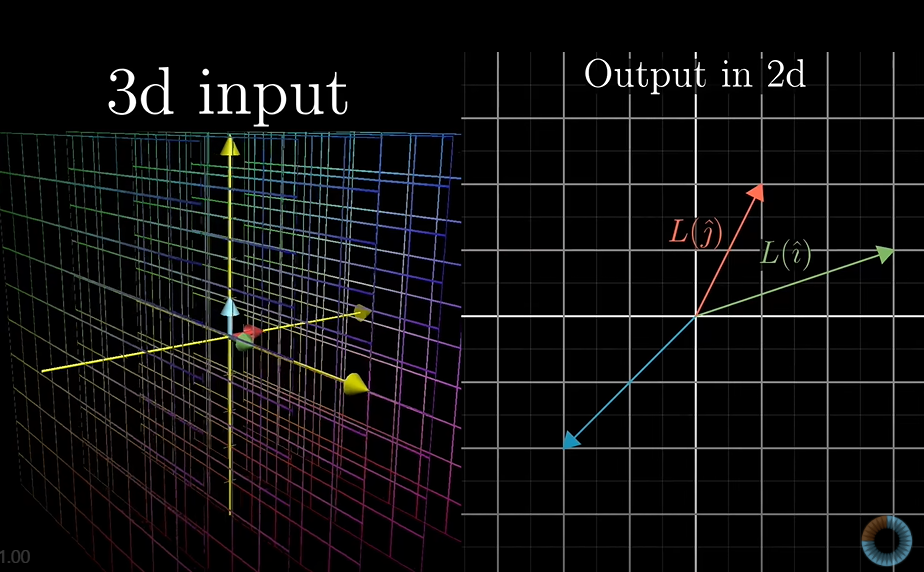
3차원에서 2차원 공간으로의 변환입니다. 일종 투사, 투영이라 합니다.
1x2 matrix
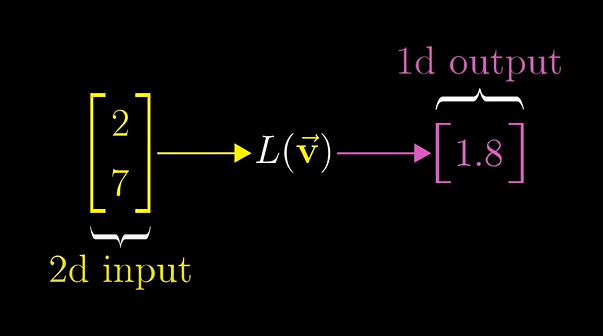
2차원에서 1차원으로 이동하는 변환도 가능합니다.
1차원은 그저 단지 하나의 선입니다. 그래서 2차원 벡터입력을 받아 결과로 숫자 하나를 내놓습니다.
위의 예에서 일어나는 축소 변환은 골치 아프다고 합니다.

두 열은 기저벡터의 도착지를 의미하는데 하나의 숫자로 표현됩니다. 이건 dot product와 관련해서 의미를 갖고 있다고 합니다.
이것은 다음 Chapter9에서 더 자세히 다룬다고 합니다! Ch8은 단순히 예시를 보여주고 어떻게 될 지 궁금증을 유발하고 있네요!
그 전 행렬 곱셈과 선형방정식계에 대한 고민을 하고 오라고 합니다!
