The determinant(행렬식)
예전에 선형대수학 수업을 들었을 때, 행렬식에 대해 배웠었다. 행렬식(determinants)이란
- 역의 존재
- 역수의 존재(ab=1을 만족하는 실수 a의 역수 b가 존재할 조건은 a != 0 일 때)- 역 행렬의 존재(AB=I을 만족하는 행렬 A의 역행렬 B가 존재할 조건: det(A) != 0)
- 행렬식
- 임의의 정방 행렬의 역행렬 존재 여부, 즉 특이성(singularity) 판단에 사용한다.
이 말은 즉, 행렬식이란 역행렬이 존재하는 비특이 행렬이어야만 조건이 성립할 수 있다는 것이다.
이 영상에선 determinant를 어떻게 다루고 있을지 궁금하네요.😉
How much are areas scaled?
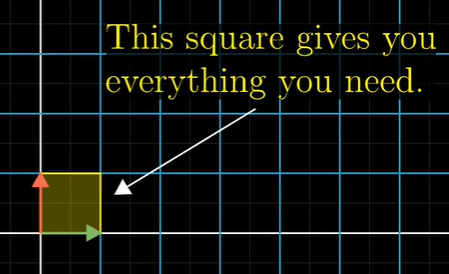
특정 지역의 크기를 증가하거나 감소시키는 팩터(factor) 요인값을 측정해보는 방법이 있다.
Generally stretches space
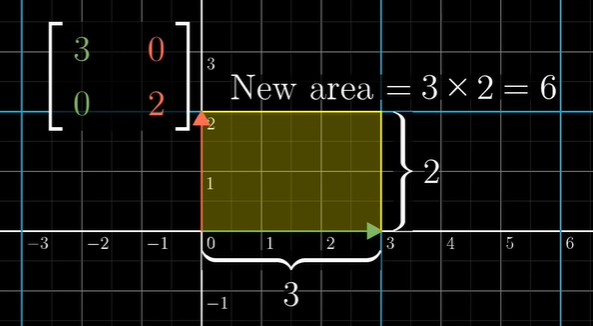
1x1 행렬이었다면 위의 노란색 영역처럼 확대된다. 영역의 크기가 6으로 바뀌었다.
그렇다면, 이 선형변환은 팩터 6으로 영역(area)를 확장시킨다고 말할 수 있다.
Generally squishes space
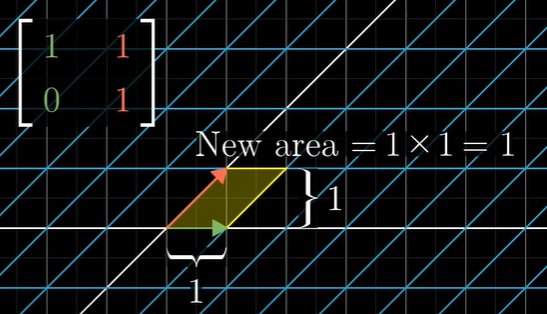
위는 영역이 줄어드는 것처럼 보여도 평행사변형의 넓이는 1로 같다.
The "determinant" of a transformation
선형변환의 행렬식 계산하는 방법은 뒤에서 설명할 것이고, 예시를 이미지로 가볍게 살펴봅시다.
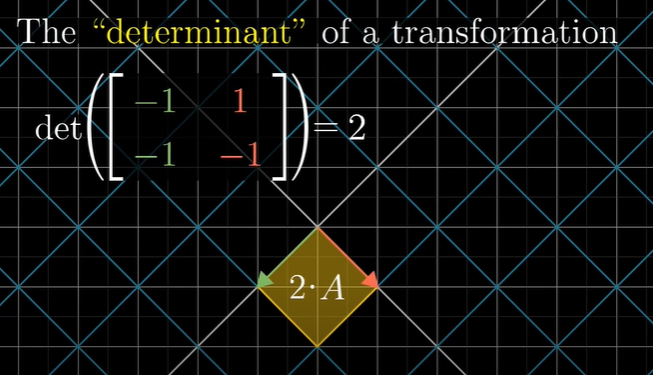
(예시 1)
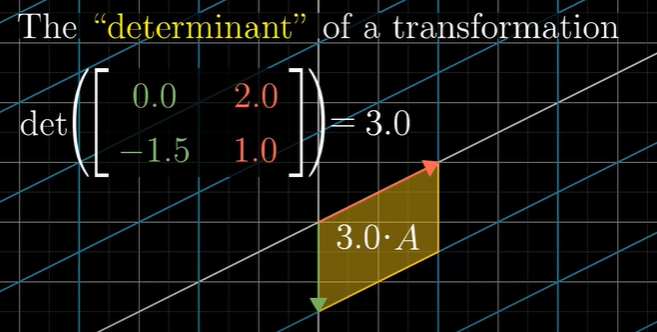
(예시 2)
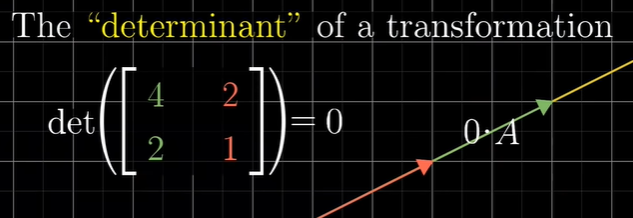
(예시 3)
예시 3의 경우는 아주 중요한 예시입니다. 왜냐하면 2차원 변환의 행렬식으로 변한 것이 아닌 1차원 직선으로 변화했기 때문에 area가 0이 되었기 때문입니다!
주어진 행렬식(determinant) 값이 0인지 확인하는 것은 계산할 수 있는지 없는지를 알려줍니다.
det(M) < 0 ?
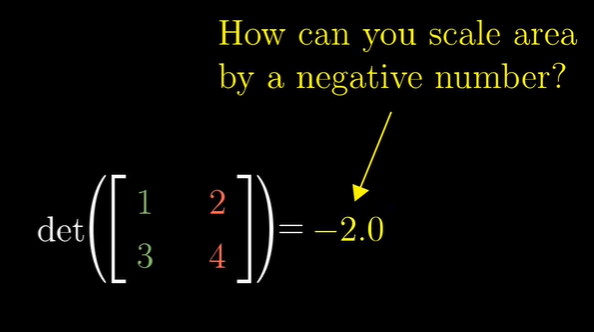
How can you scale area by a negative number?
행렬식은 당연히 음수값도 허용합니다. 그렇다면 영역을 생각할 때 음수는 어떻게 생각해야 하는 걸까요?
이것은 방향(orientation)과 관계가 있습니다.
하지만 행렬식의 절대값이 영역 스케일링에 관한 팩터로 생각할 수 있습니다. 음수는 그저 방향을 전환한다는 것을 의미하기 때문입니다. 영역의 크기와는 무관함!
3차원의 행렬식, volume(부피)
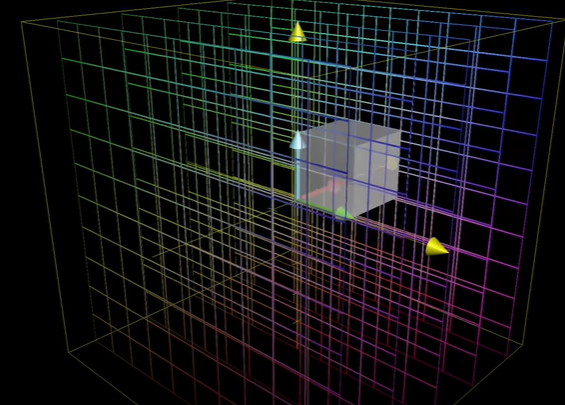
3차원에서도 1x1x1 큐브 모양의 정육면체를 떠올린다면 쉽습니다. 이의 부피를 계산하는 것도 어렵지 않죠.

여기서도 행렬의 값이 0이 된다면, 이 모든 부피가 찌부러뜨려서 0이 된다고 생각하면 됩니다.
Linearly Dependent

위의 계산 식을 보면 선형 독립(Linearly Dependent)이라고 떠올릴 수 있습니다.
3차원 공간에서의 음수 영역은 무엇을 의미할까요? 3차원에서 똑같이 방향 전환으로 설명하고 있습니다. 이 방향은 3곳을 의미하겠죠. x, y, z의 3개의 축이 있으니까요.
det(M) = ad - bc
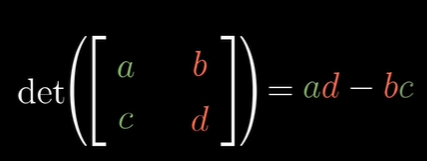
2차원 행렬의 경우엔 이렇게 계산을 해줍니다.

물론 3차원 행렬도 구하는 방식이 있습니다!😂 하지만 3차원 이상부터는 계산하는 방법을 확실하게 연습해야 헷갈리지 않고 풀 수 있게 됩니다.
대학교에서는 5차원 행렬의 역행렬을 구하라. 라는 문제가 나오기도 했는데 이건 정말 노가다의 끝판왕이었지요. 이 영상에서도 설명하는 사람은 이런 계산은 선형대수의 본질은 아닌 것 같다고 말하고 있습니다. 저도 이 소신 발언에 동참하고 싶습니다.😏
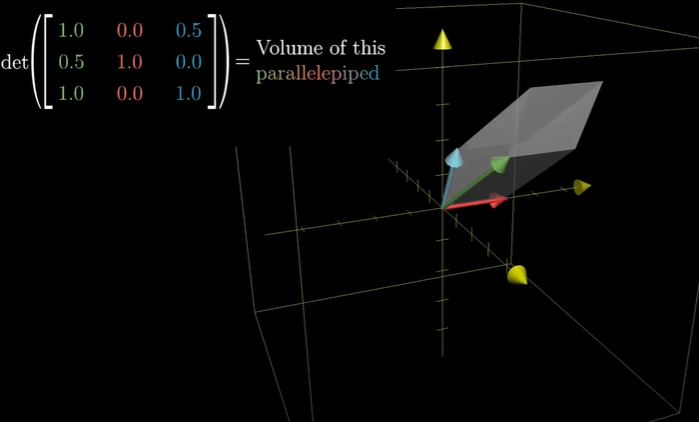
이 영상에서는 계산이 아닌 행렬식이 무엇을 의미하는지, 그 본질을 이해하고 접근하는 것을 추천합니다!
Quiz!
det(M1M2) = det(M1)*det(M2) 일까요?
와. 영상에서는 답을 안 알려주네요? 알고보니 교수님보다 더 나쁜 분인듯...
아무튼 det(AB) = det(A)det(B) 는 성립합니다. True!
여기서는 사실 행렬의 개념이 들어가면 더 쉽게 이해할 수 있는데요.
A의 행렬이 있다면 A의 역행렬을 A-1라고 합니다. 그리고 A와 A-1를 곱하면 무엇이 되나요?
AA-1 = I
I는 단위행렬입니다. 단위행렬은 대각선의 요소가 모두 1인 행렬이고, 사실 정의로서는
AI = IA 일 때, I는 단위행렬이다.
라고 볼 수 있습니다. 왜냐하면 행렬은 AB != BA 라고 했던 것 기억나시죠? 곱셈의 교환법칙이 성립되지 않습니다. 그래서 I의 정의를 저렇게 내릴 수 있는 것입니다.
아무튼, 퀴즈의 본론으로 돌아갑시다.

이렇게 정리할 수 있겠습니다!
