Three-dimensional linear transformations
3차원의 선형변환
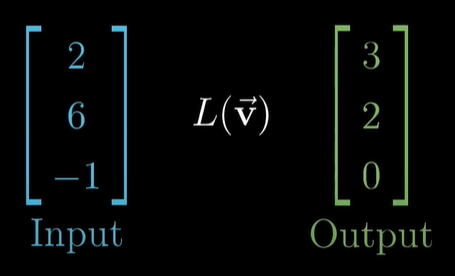
3차원 벡터를 입력 받아서 3차원 벡터를 출력합니다.
3차원 공간을 상상해 봅시다. 2차원 공간과 같이 격자선은 평행하고, 간격이 일정합니다. 원점은 고정되어 있습니다. 공간의 모든 점들은 벡터의 끝점을 대신합니다.
입력(input) 벡터를 받아서 움직여서 대엉되는 결과(output) 벡터를 만드는 것입니다. 변환은 앞에서도 말했듯이 기저 벡터의 움직임을 알면 설명할 수 있습니다.
그런데 3차원에서는 세 개의 표준 기저벡터를 표시하는 일반적인 방법이 있습니다! 😉
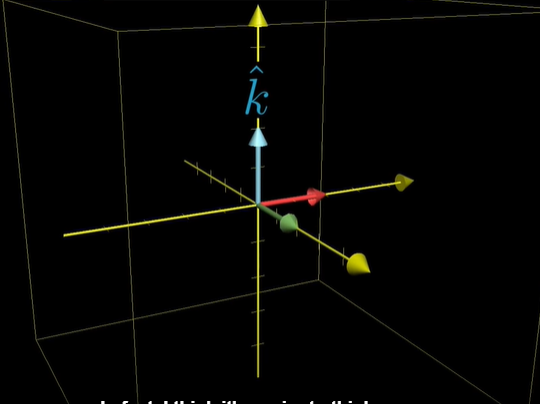
이전에 x축의 단위벡터를 무엇이라 했나요? i-hat입니다. 그럼 y축의 단위벡터는 j-hat, 그렇다면 새로운 축이 생겼습니다. z축의 단위벡터를 k-hat으로 하기로 했습니다!
이 변환들을 기저벡터로 설명하는 것이 더 쉽습니다.
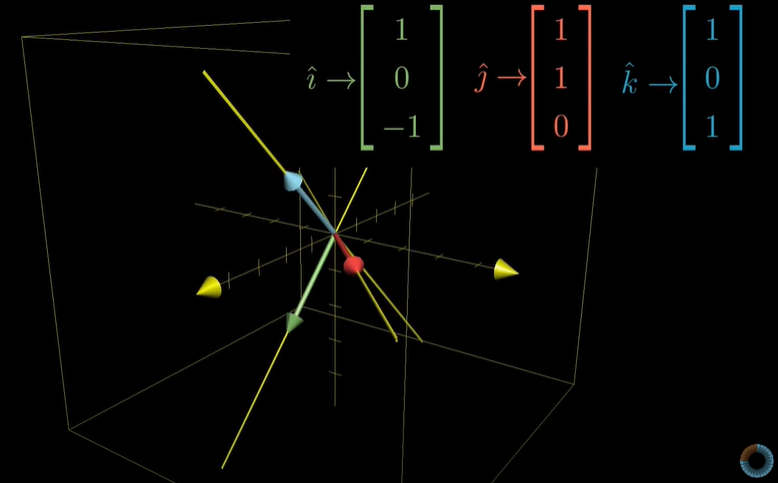
변환 후의 세 기저벡터의 좌표값만 생각하는 것입니다. 세 벡터의 좌표값을 열(column)으로 합쳐 3x3 행렬이 됩니다. 9개의 숫자로 이 변환을 완전하게 설명할 수 있는 것입니다.

3좌표값의 집합이 행렬의 열을 구성하게 되고, 행렬이 이 변환을 설명할 수 있게 됩니다.
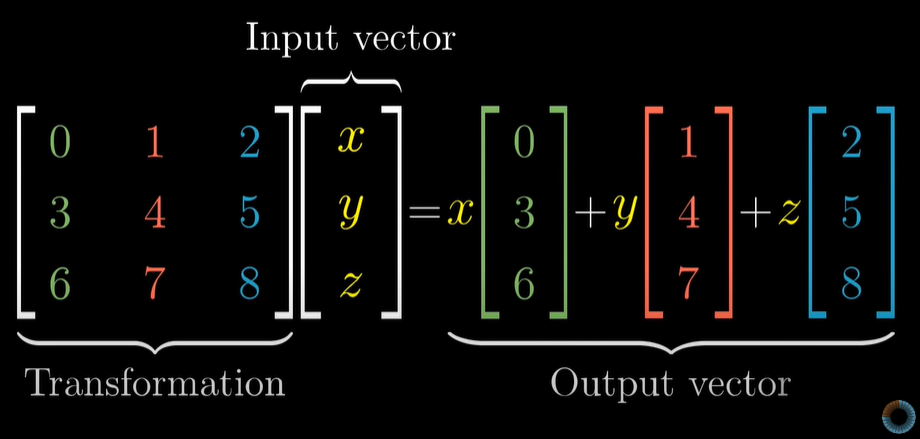
2차원에서 했던 것처럼 각 기저벡터들은 그 벡터로 스케일링해서 합치면 원하는 결과 벡터를 얻을 수 있는 것과 동일합니다.
그래서 벡터의 변환 결과를 알려면, 벡터의 좌표값을 행렬에 대응되는 열과 곱한 다음 그 결과들을 합하면 됩니다.
이전의 4강 행렬의 곱에서도 마찬가지로 오른쪽 행렬을 기준으로 먼저 변환 처리 되고, 왼쪽 행렬이 그 다음 변환 처리 됩니다.
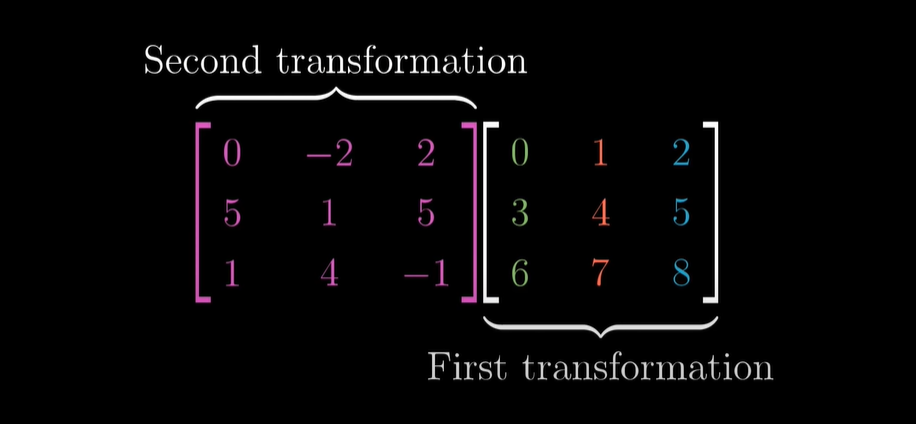
이 (3x3)행렬과 (3x3)행렬의 곱셈을 한 번 직접 계산해 보세요!
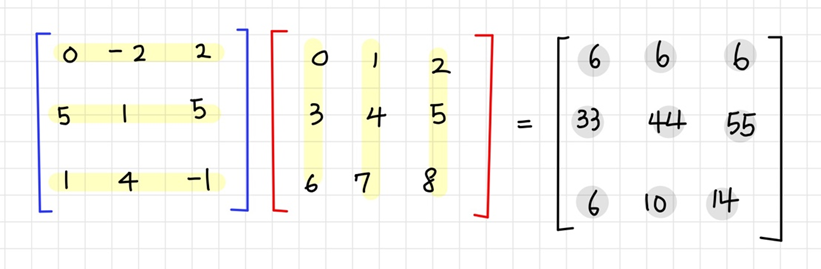
저도 풀어봤습니다😏
