Matrix multiplication as composition
3강 Review: 선형 변환
기저 벡터가 선형 변환에 의해 어떻게 옮겨졌는지를 알면 그 선형 변환이 무엇인지 파악할 수 있습니다.
예를 들어, 2차원 공간에서는 i-hat, j-hat으로 말입니다. 모든 벡터들은 i-hat, j-hat의 선형 결합으로 모두 표현이 가능하기 때문입니다.
선형 변환 이후,
- 격자선들이 평행을 유지
- 균등 간격 유지
i-hat, j-hat의 변형 후 좌표값을 행렬로 표현하며, 이 열들 각각을 x, y로 스케일링 한 것을 행렬-벡터 곱셈으로 정의합니다.
이 관점에서 한 행렬은 하나의 선형변환을 나타낸다고 볼 수 있습니다.
First rotation then shear

회전과 옆으로 미는 것도 션형봔한이고 이 둘을 선형변환의 합성이라 일컫습니다.
"Composition of a rotation and a shear"
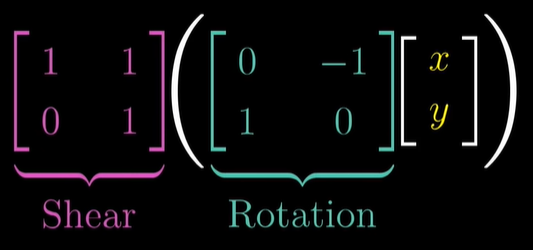
어떤 벡터에 회전 시키고 민 것을 수치적으로 표현하면 위와 같습니다.
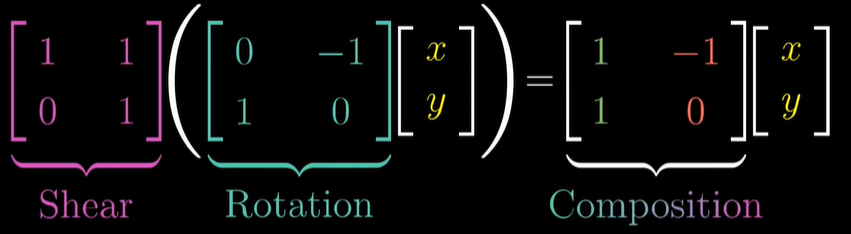
하지만 여기서 Composition 행렬을 곱해도 같은 결과 값을 같습니다.
여기서 rotation과 shear을 통해 설명하고자 하는 바가 무엇인지 느껴지시나요? 행렬의 곱에 대해 설명해주려고 하는 것 같습니다.
행렬의 곱(product)
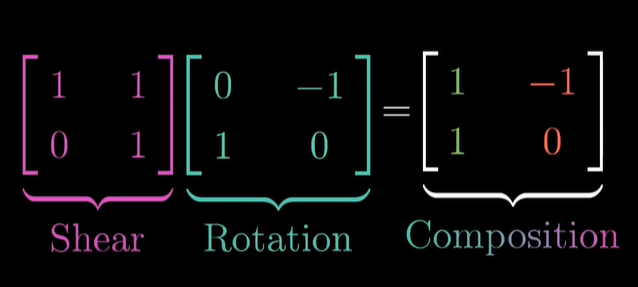
Composition은 두 원본 행렬의 곱(product)라고 부를 수 있습니다.
행렬을 아마 처음 마주한다면 행렬의 곱셈 방식에 어색할 수 있습니다.
행렬의 곱은
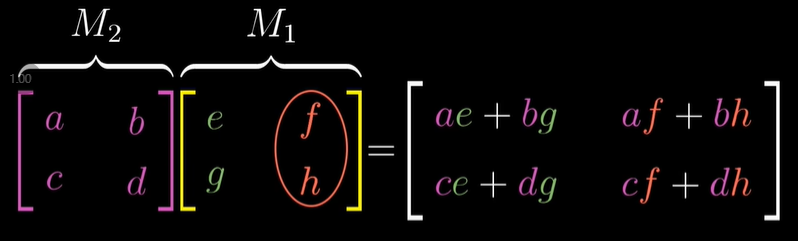
이 이미지를 참고하여 주시면 되겠습니다.
두 행렬의 곱셈은 기하학적으로 한 변환을 적용하고 나서 다른 변환을 적용한다는 것과 같은 의미입니다.
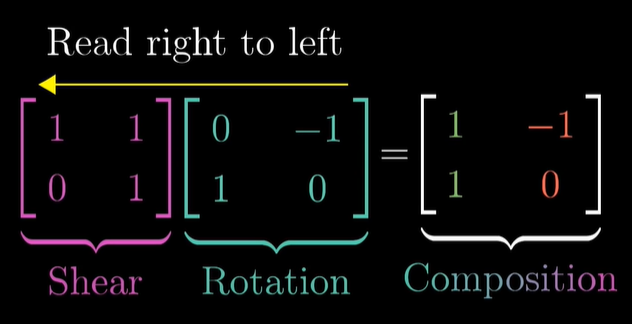
여기서 하나 알려주고 있는 점은, 읽을 때 오른쪽에서 왼쪽 방향으로 봐야한다는 점입니다. 우측 행렬이 첫 번째 변환을 나타내고, 좌측의 행렬이 그 다음 변환 적용입니다.
이는 함수 표기법이랑 연관이 있는데 합성 함수를 떠올린다면 오른쪽에서 왼쪽으로 읽어야 합니다.
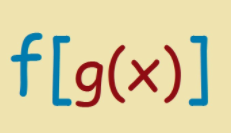
Example
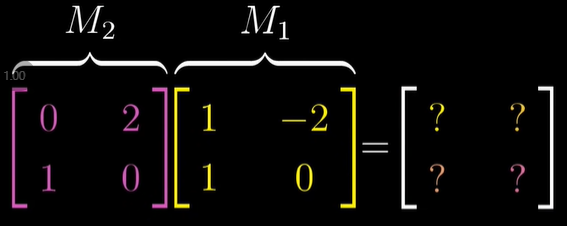
M1, M2의 선형변환 행렬이 있다고 생각해 봅시다.
- i-hat 좌표는 무엇인가요?
- M1의 첫 번째 열입니다. (1,1)
- 이를 M2와 곱해주면 합성 행렬의 첫 번째 열을 얻을 수 있습니다.
- j-hat 좌표는 무엇인가요?
- M1의 두 번째 열입니다. (-2,0)
- 이를 M2와 곱해주면 합성 행렬의 두 번째 열을 얻을 수 있습니다.
행렬의 곱 규칙들
- AB != BA
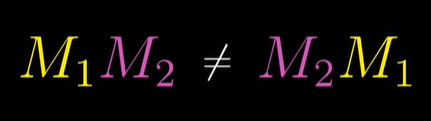
- (AB)C == A(BC)
행렬의 결합 법칙을 행렬의 곱셈을 한 변환을 적용하고 나서 다시 다른 변환을 적용하는 관점으로 생각하는 것이 더 좋습니다.
정리
선형변환, 선형결합, 기저벡터의 변형 등 1~4강을 통해 기본적인 것을 공부하였는데요. 밑의 글을 읽어보고 한 번 생각해보며 정리하는 것도 좋을 것 같습니다.
행렬과 벡터의 곱이 열벡터의 선형결합이라는 것은 행렬과 벡터의 곱을 기저 벡터의 변형을 통한 벡터의 선형 변환으로 해석할 수 있습니다.
