"불행히도, 아무도 매트릭스가 무엇인지 말할 수 없으니 직접 봐야합니다."
- 영화, [매트릭스] 모피어스
다들 영화 매트릭스 보셨나요? Matrix가 무엇일까요?😁
Matrices as Linear transformations
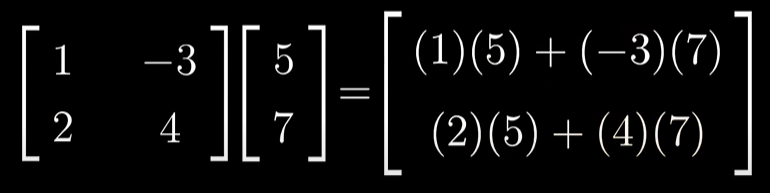
Linear transformations(선형변환)
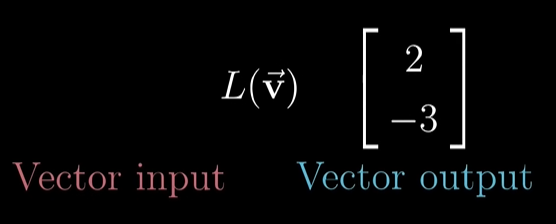
선형변환
입력을 받고 결과물을 반환하는 무엇
특정 벡터를 다른 벡터로 바꾸는 변환 같은 것입니다.
"함수(function)"라는 말대신 "변환(transformation)"이라는 말을 사용합니다.
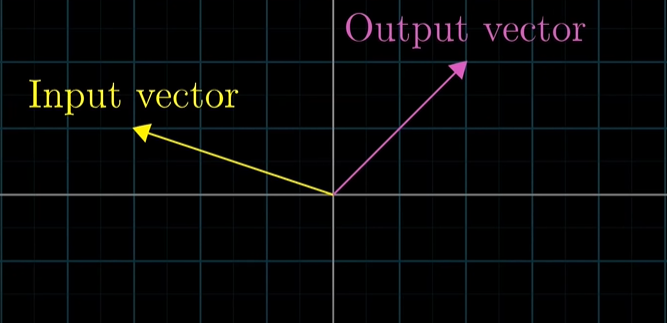
입력 벡터를 이동시켜서 출력 벡터로 만드는 것으로 생각해볼 수 있습니다.
선형변환 속성
선형대수에서는 특수한 형태의 변환으로만 제한됩니다.
변환이 '선형적(linear)'이라는 건 두 가지 속성을 의미합니다.
- 모든 선들은 변환 이후에도 휘지 않고 직선이다.(Lines remain lines)
- 원점은 변환 이후에도 여전히 원점이어야 합니다. (Origin remains fixed)
선형변환이라면 격자 라인들이 변형 이후에도 여전히 '평행'하고 '동일한 간격'으로 있어야 합니다.
어떻게 결과 벡터 좌표값이 나오도록 할 수 있을까요?

결론은 두 개의 기저벡터(i-hat, j-hat)가 어떻게 변하는지만 알면 됩니다.

이 선들이 계속 평행하고 균등하게 분포한다는 속성을 알 수 있습니다.
변환 후 v는 변환된 i-hat 벡터의 -1배, 변환된 j-hat 벡터의 2배입니다.
즉, 변환 전 v벡터를 이루는 i-hat과 j-hat의 어떤 선형 결합이 변환 후에도 같은 선형결합을 유지합니다.
단순히 i-hat과 j-hat의 변형 위치만 알면, 벡터 v를 추론할 수 있다는 것을 의미합니다.
v벡터는 [5, 2]로 변환되었습니다.
Matrix
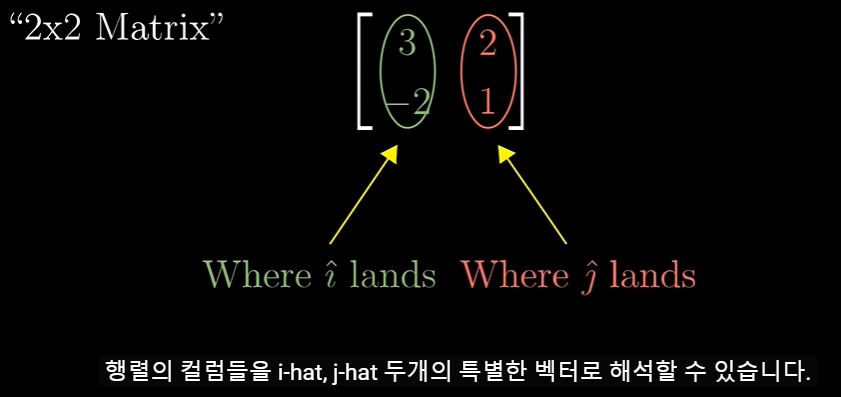
이것을 2x2 Matrix로 표현할 수 있습니다. 행렬의 컬럼들을 i-hat, j-hat 두 개의 특별한 벡터로 해석할 수 있습니다.
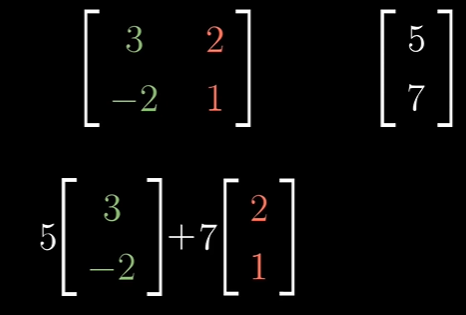
이 식은 변환 후 새 기저 벡터들로 스케일링하고 합한다는 개념입니다.
첫 번째 열은 첫 번째 기저 벡터의 도착점이고 두 번째 열은 두 번째 기저 벡터의 도착점입니다.
헹렬 벡터 연산으로 함수와 같은 결과를 얻을 수 있습니다.
하지만 결과 벡터를 기저벡터의 변환으로 생각하면 더 좋습니다!
벡터가 선형 종속일 때
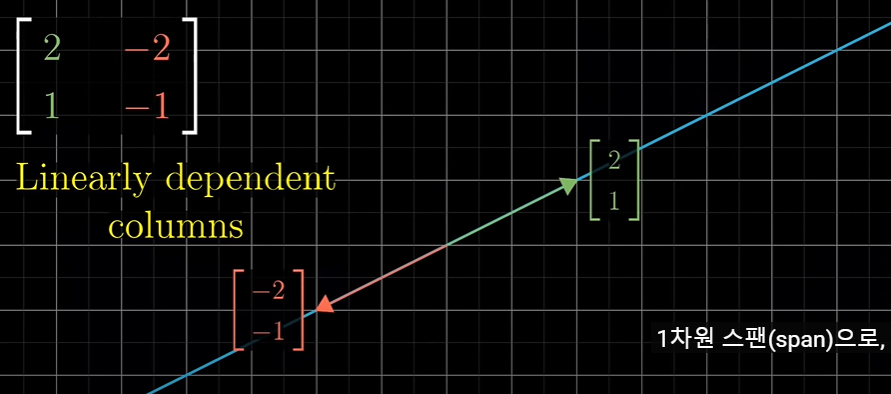
i-hat, j-hat 벡터가 선형 종속(Linearly Dependent)이라면 벡터 하나가 다른 벡터의 스케일링 버전임을 뜻합니다.
즉, 이 선형 변환은 2차원 공간을 수축(squish) 시켜 두 벡터가 놓여 있는 선으로 만드는 것을 의미합니다.
1차읜 span이 만들어지는 것입니다.
정리
선형변환은 공간을 이동시키는 방법이며 격자선이 여전히 평행하고 균등 간격을 유지하는 변형입니다. 그리고 원점은 고정되어 있음을 의미합니다.
기저벡터들의 변형 후 좌표 값은 행렬이 어떠한 변환을 설명해주고 행렬-벡터 곱셈은 단지 이것을 계산하는 방법입니다.
선형대수에서는 행렬을 공간의 어떤 변환으로 생각해야 합니다.
이 강의의 진도

