[3BlueBrown] Vectors | Chapter 1

1강 Vector 강의

Vector

선형대수에 기반하는 벡터의 기본 연산

1. 벡터의 합
2. 벡터의 곱

• 선형대수의 벡터는 원점에 뿌리를 둔다.

• 숫자 리스트는 벡터의 좌표를 의미
  리스트 형태로 벡터를 두는 건 기하학적 해석이다.
  ex. [-2, 3]

• 모든 숫자쌍은 각각 하나의 벡터와 대응되고 반대로 모든 벡터는 각각 대응되는 숫자쌍이 하나있습니다.

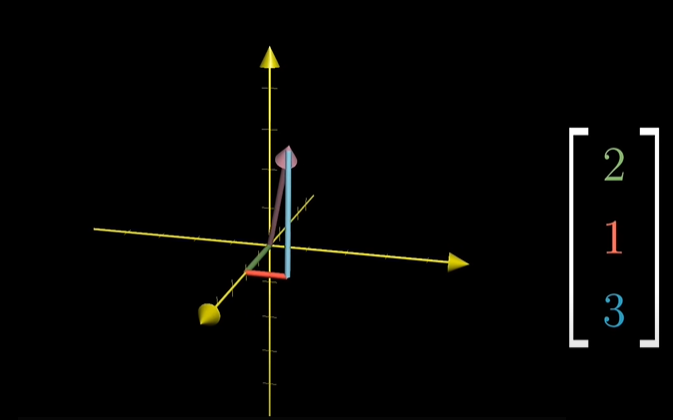
• 3차원은 2차원에서 축이 하나 추가 되는 것

선형대수는 두 종류의 연산으로 이루어진다.

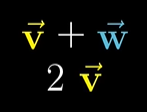
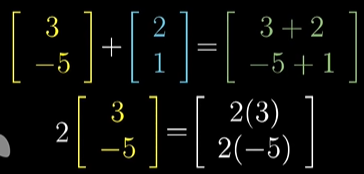
벡터는 공간에서 특정한 방향과 거리를 가진 움직임을 생각하면 쉽다. 첫 번째 벡터에 따라 이동하고 두 번째 벡터에 따라 이동하면 두 벡터에 따라 이동한 것과 같다.

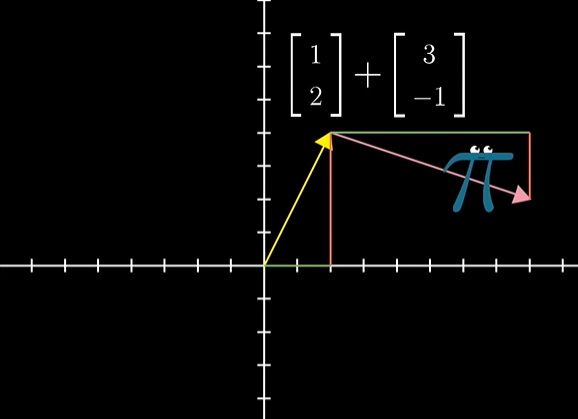
위의 이미지에서 벡터의 합이 새 벡터의 좌표가 된다. 일반적으로 숫자-리스트 컨셉에서 벡터합은 항끼리 매칭해서 서로 더하는 것처럼 보여진다.

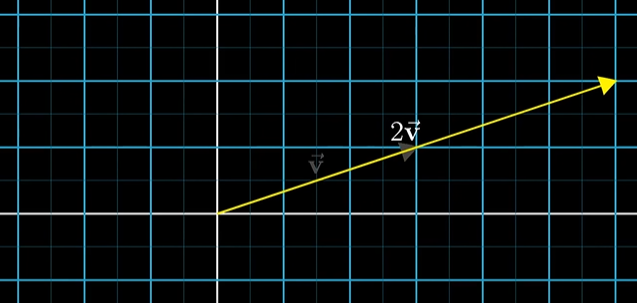
벡터의 곱의 연산은 벡터를 기존의 n배 만큼 늘리는 것을 의미한다. 위에는 2를 곱했더니 기존 벡터에서 2배만큼 길어진다.

만약 1/3을 곱한다는 것은 1/3로 길이를 줄이는 것을 의미하고 -1.8은 반대 방향(음수 방향으로 가기 위한)으로 1.8배 늘린 것을 의미한다.

Scaling and Scalars

이렇게 벡터의 길이를 늘이거나 줄이거나 방향을 뒤집는 것은 "스케일링(scaling)" 이라고 한다. 그리고 벡터 스케일링에 사용되는 숫자들을 ""스칼라(scalar)"" 라고 한다.

→ 스칼라는 벡터를 스케일링한다.

그 뒤에 배울 선형대수는 벡터합과 스칼라곱과 모두 연관되어 있다. 숫자 리스트들을 가상적 공간에서 개념화하는 방법을 배울 수 있고, 데이터의 패턴을 명확하게 해준다.

2강에서 배우는 것

Linear combinations, span and bases