[DL] 가중치 초기화(Weights Initialization)

참고 자료

📚 딥러닝 교과서, 출판사: 이지스 퍼블리싱

목차

1. 참고 자료
2. 목차
3. 상수 초기화
   • 가중치를 0으로 초기화
   • 가중치를 상수로 초기화
4. 가우시안 분포 초기화
   • 가중치를 아주 작은 난수로 초기화
   • 가중치를 아주 큰 난수로 초기화
   • 적정한 가중치
5. Xavier 초기화
   • Xavier 초기화 방식의 가정
   • Xavier 초기화 식의 유도 과정
6. He 초기화
7. Summary

신경망을 학습할 때 손실 함수의 어느 위치에서 출벌해야 최적해가 있는 곳으로 더 쉽고 빠르게 도달할 수 있을까요?

최적해 근처에서 출발한다면 더 빨리 되겠지만, 최적해가 어디 있는지 모르는 상태에서 어디서 출발하는게 가장 좋을까를 생각해보는 것이 이번 파트입니다.

신경망을 학습할 때 손실 함수에서 출발 위치를 결정하는 방법이 모델 초기화(Initialization)입니다.

특히 가중치는 모델의 파라미터에서 가장 큰 비중을 차지합니다. 가중치 초기화 방법에 따라 학습 성능이 크게 달라집니다.

상수 초기화

최적해에 대해 정보가 없을 때 생각할 수 있는 방법으로 임의의 상수로 초기화하는 것입니다.

가중치를 0으로 초기화

신경망의 가중치를 모두 0으로 초기화했다고 가정합니다.

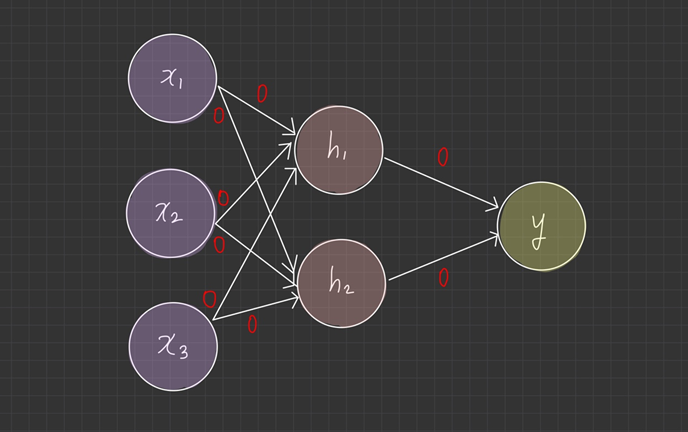
뉴런의 가중치가 0이면 가중합 결과는 항상 0이 됩니다. activation function은 가중 합산 결과인 0을 입력 받아서 늘 같은 값을 출력하게 됩니다.

$z=w^Tx+b=0$
$a=activation(x) \in {0,0.5}$

예를 들어 활성 함수가 ReLU나 tan$h$이면 출력은 0이 되고, sigmoid이면 0.5의 값이 나옵니다.

또한, 출력 뉴런의 활성 함수가 softmax일 경우, 모든 클래스의 확률이 동일하게 균등 분포를 출력합니다.

결과적으로 의미 없는 결과가 만들어지며, 가중치가 0이면 학습도 진행되지 않습니다.

다음과 같이 역전파 과정에서 뉴런의 local gradient는 $w$이므로 항상 0이 됩니다.

다음 뉴런에 전달할 global gradient

도 0이 되기 때문에 학습이 진행되지 않습니다.

가중치를 상수로 초기화

이번엔 가중치를 0.1로 초기화한다고 가정하겠습니다.

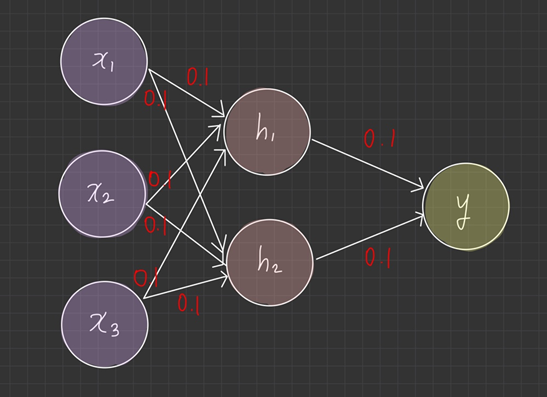
두 개의 은닉 뉴런 $h_1$과 $h_2$는 입력 $(x_1, x_2, x_3)$과 가중치가 (0.1, 0.1, 0.1)로 같기 때문에 가중 합산 결과도 같고, 활성 함수의 실행 결과도 같습니다.

실제 뉴런은 2개지만 1개만 있는 것과 똑같은 의미입니다. 출력 뉴런 $y$는 $h_1$과 $h_2$에서 같은 값을 입력 받으므로 정보가 반으로 줄어들고, 연산 결과도 부정확해집니다.

이처럼 가중치를 모두 같은 상수로 초기화하면 신경망에 대칭성(symmetry)이 생겨서 같은 계층의 모든 뉴런이 똑같이 작동하게 됩니다.

가우시안 분포 초기화

대칭성을 피하려면 가중치를 모두 다른 값으로 초기화하는 방법이 있습니다.

이제 가중치를 균등 분포나 가우시안 분포를 따르는 난수(random number)를 이용해서 초기화 해보려고 합니다.

가중치 초기화가 계층별 데이터 분포와 학습에 미치는 현상을 설명하기 위해 다음과 같은 10계층 모델을 가정하였습니다.

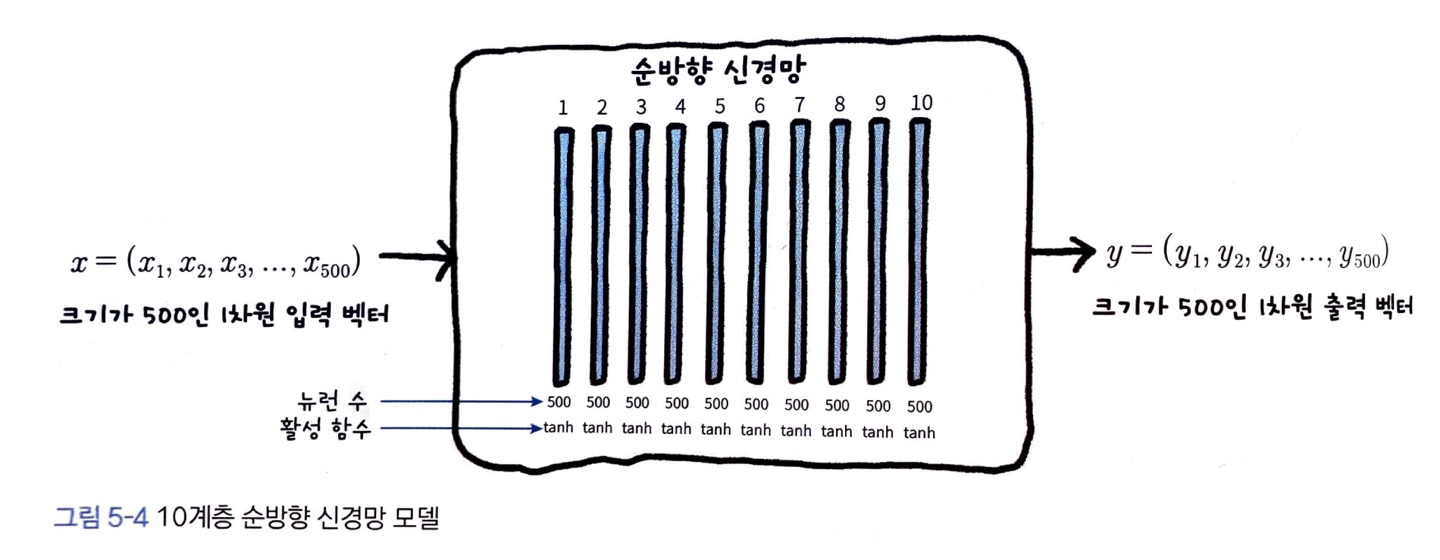
• 각 계층에는 500개의 뉴런이 있음
• 입력 데이터는 크기가 500인 실수 벡터이며, 가우시안 분포 $N(0,1)$을 따르는 난수로 생성

가중치를 아주 작은 난수로 초기화

모델의 가중치를 가우시안 분포 $N(0,0.01)$을 따르는 난수로 초기화합니다.

평균이 0, 분산이 0.01으로 아주 작은 값으로 초기화 되었습니다.

신경망에 입력된 데이터 10개의 layer를 지나며, 다음과 같은 분포로 변화합니다.

계층이 깊어질수록 출력이 점점 0으로 변화합니다.

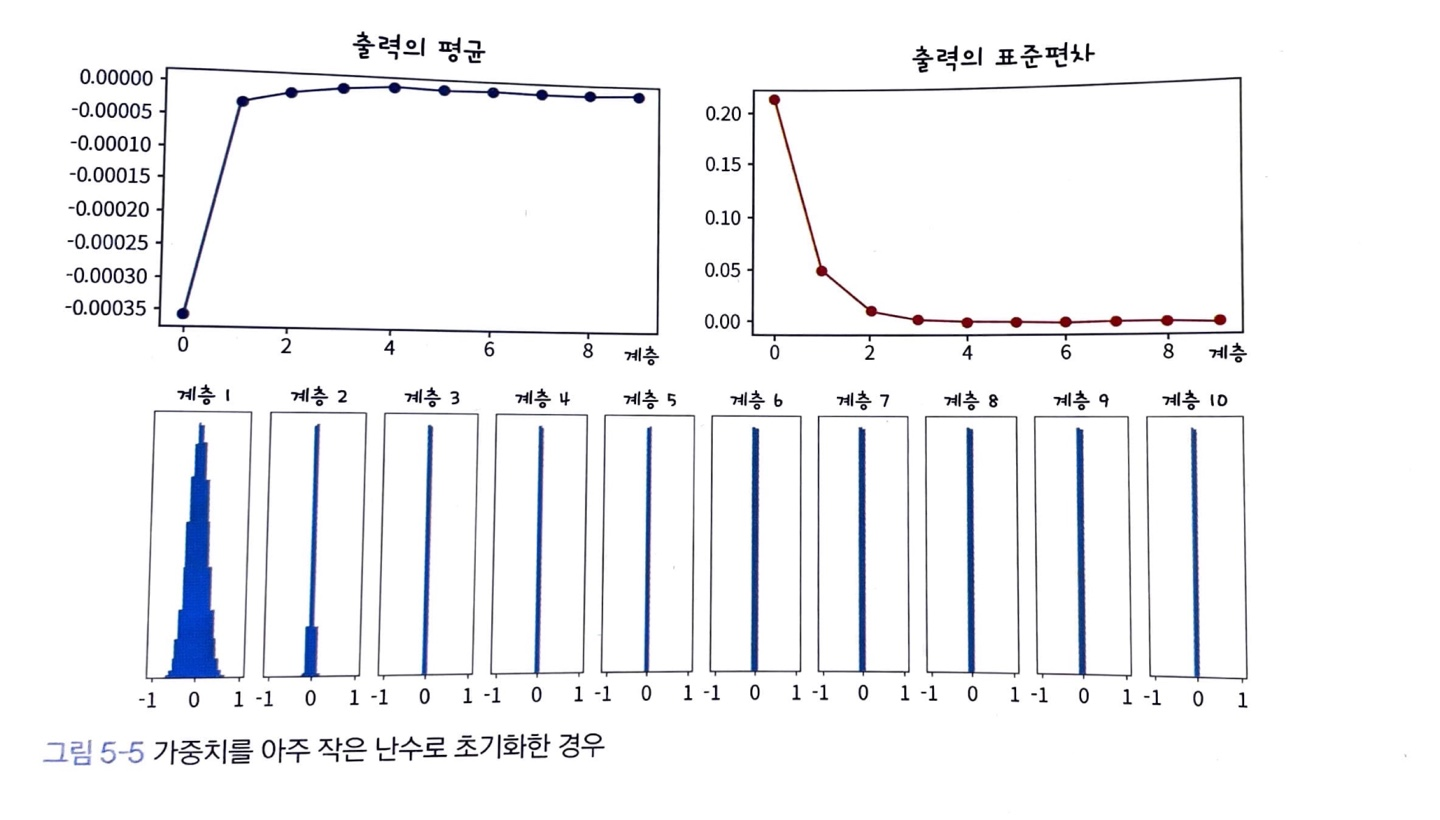
가중치가 너무 작은 경우, 뉴런의 출력도 작아집니다.

입력 계층이 여러 layer를 지날수록 점점 0에 가깝게 변하며, 값이 0이 되는 순간 뉴런의 가중 합이 0이 되어서 의미 있는 출력과 학습을 진행하지 못하고 초기화 했을 때랑 비슷한 현상이 일어납니다.

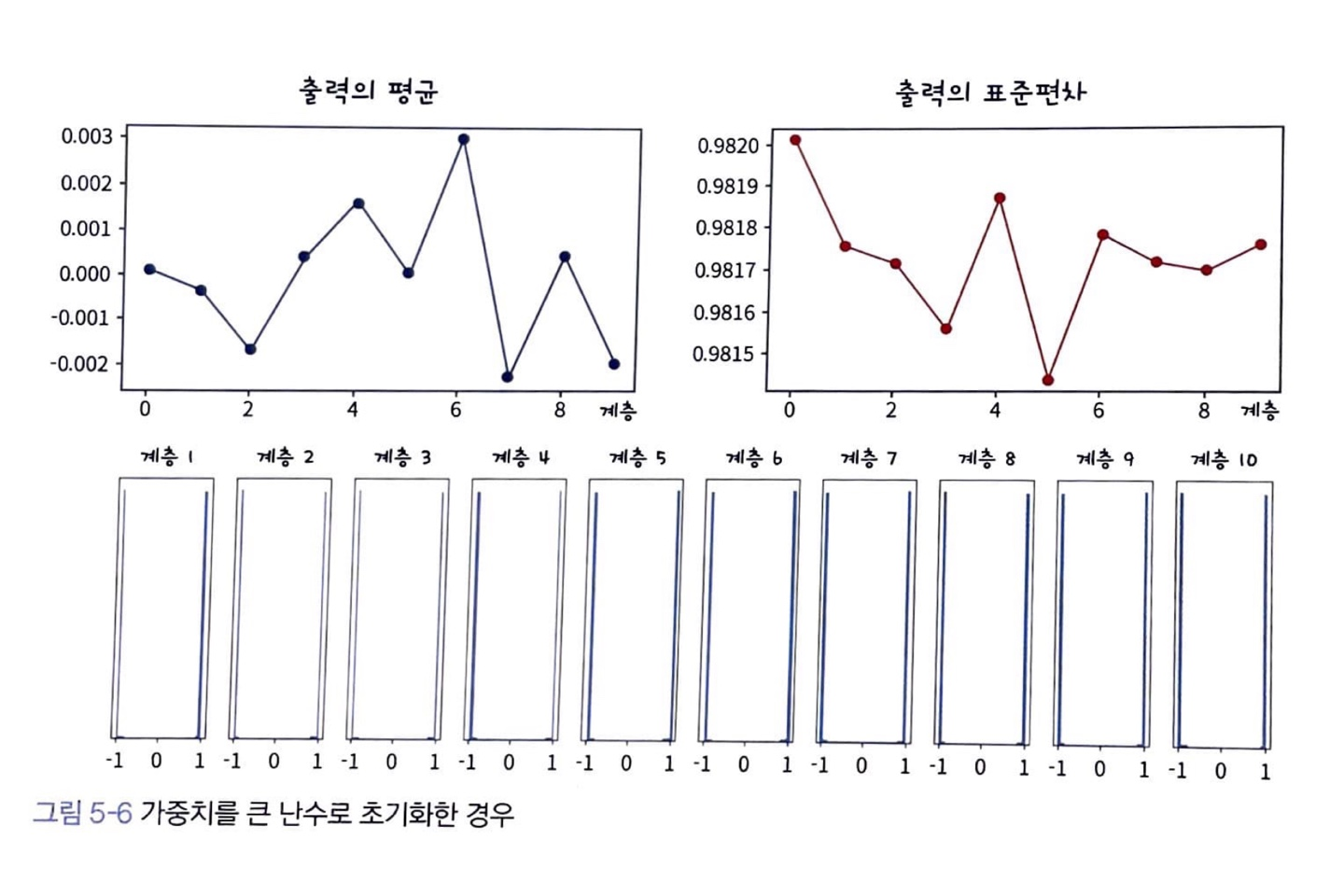
가중치를 아주 큰 난수로 초기화

이번엔 가중치를 크게 만들어 가우시안 분포 $N(0,1)$로 초기화 해보겠습니다.

이런 경우 입력 데이터가 layer를 지나며 점점 -1이나 1로 변하는 것을 볼 수 있습니다.

적정한 가중치

가중치가 작거나 큰 것이 모두 문제가 되었습니다. 가중치는 적어도 데이터의 크기를 줄이거나 늘리지 않는 값이어야 합니다.

데이터가 계층을 통과하더라도 데이터의 크기를 유지해주는 가중치로 초기화 해야한다.

이제 그 방법을 살펴보겠습니다.

Xavier 초기화

Xavier Initialization는 sigmoid 계열의 activation function을 사용할 때, 가중치를 초기화하는 방법입니다.

입력 데이터의 분산이 출력 데이터에서 유지되도록 가중치를 초기화합니다.

Xavier 초기화 방식의 가정

Xavier 초기화 방식을 유도하기 위해 몇 가지를 가정해보겠습니다.

1. 활성 함수를 선형 함수로 가정한다.

• 입력 데이터가 0 근처의 작은 값으로 되어 있다.
• 이 경우 입력 데이터는 시그모이드 계열의 활성 함수의 가운데 부분을 지난다.
• 시그모이드 계열의 활성 함수 가운데 부분은 직선에 가깝기 때문에 선형 함수로 가정할 수 있다.

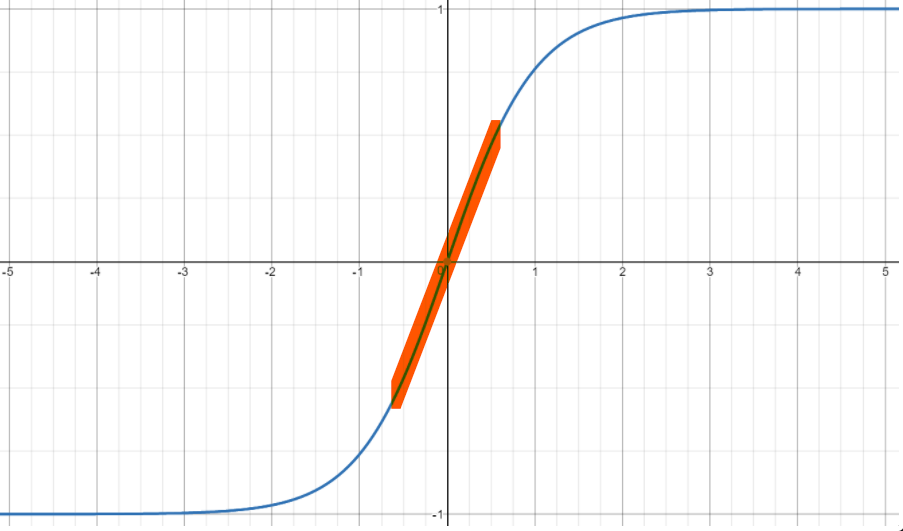
• 하이퍼볼릭 탄젠트 함수의 선형성

2. 입력 데이터와 가중치는 다음과 같은 분포의 성질을 가진다.

• 입력 데이터 $(x_1, x_2, ..., x_n)$와 가중치 $(w_1, w_2, ..., w_n)$은 서로 독립이다.
• 입력 데이터의 각 차원 $x_i$는 같은 분포이고 서로 독립인 i.i.d를 만족한다.
• 가중치의 각 차원 $w_i$도 같은 분포이고 서로 독립인 i.i.d를 만족한다.
• 각 $x_i$와 $w_i(i=1,2,...,n)$은 평균이 0인 분포를 따른다. 즉, $E(w_i)=0$이고 $E(x_i)=0$이다.

Xavier 초기화 식의 유도 과정

이제 Xavier 초기화 식을 유도해보겠습니다.

활성 함수를 선형 함수로 가정했으므로 뉴런의 출력 y는 가중 합산 z와 같습니다.

이 식의 양변에 분산을 계산하면 $x_i$와 $w_i$가 독립이므로 두 번째 줄이 유도됩니다.(n은 입력 데이터의 개수)

$E(w_i)=0$이고 $E(x_i)=0$이므로 다음과 같이 $Var(x_iw_i)=Var(x_i)Var(w_i)$를 만족합니다.

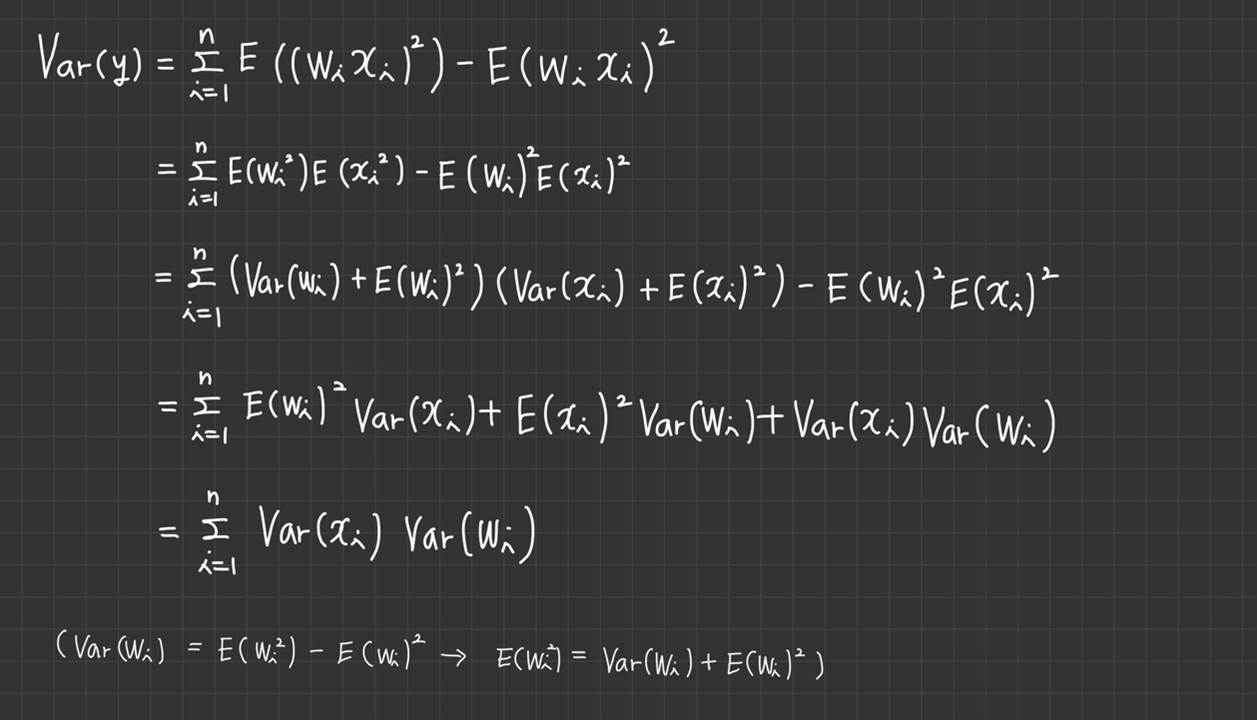
모든 $x_i$는 같은 분포를 따르므로 분산이 같고 모든 $w_i$도 같은 분포를 따르므로 분산이 같아서 다음과 같이 식이 바뀝니다.

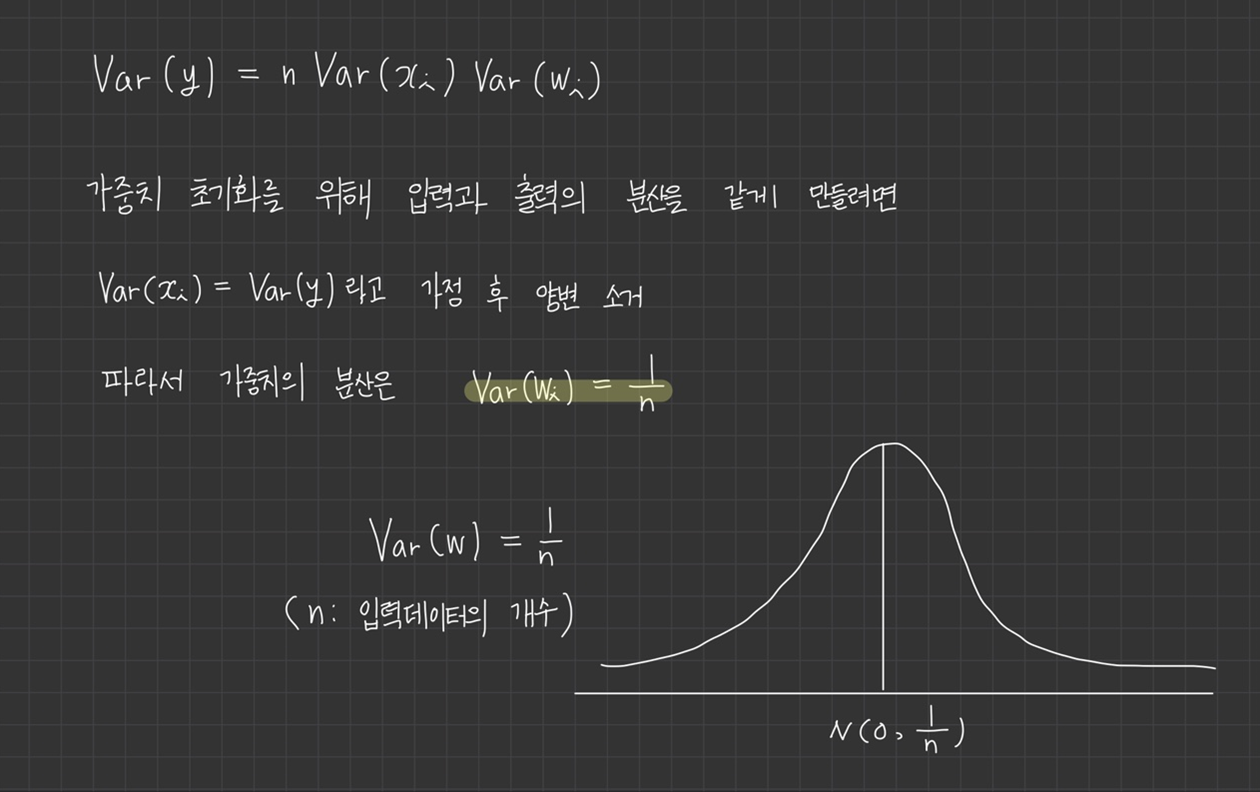
Xavier 초기화는 가중치의 분산이 입력 데이터에 개수 n에 반비례하도록 초기화하는 방식입니다.

가중치 분포는 가우시안 분포 또는 균등 분포로 정의합니다.

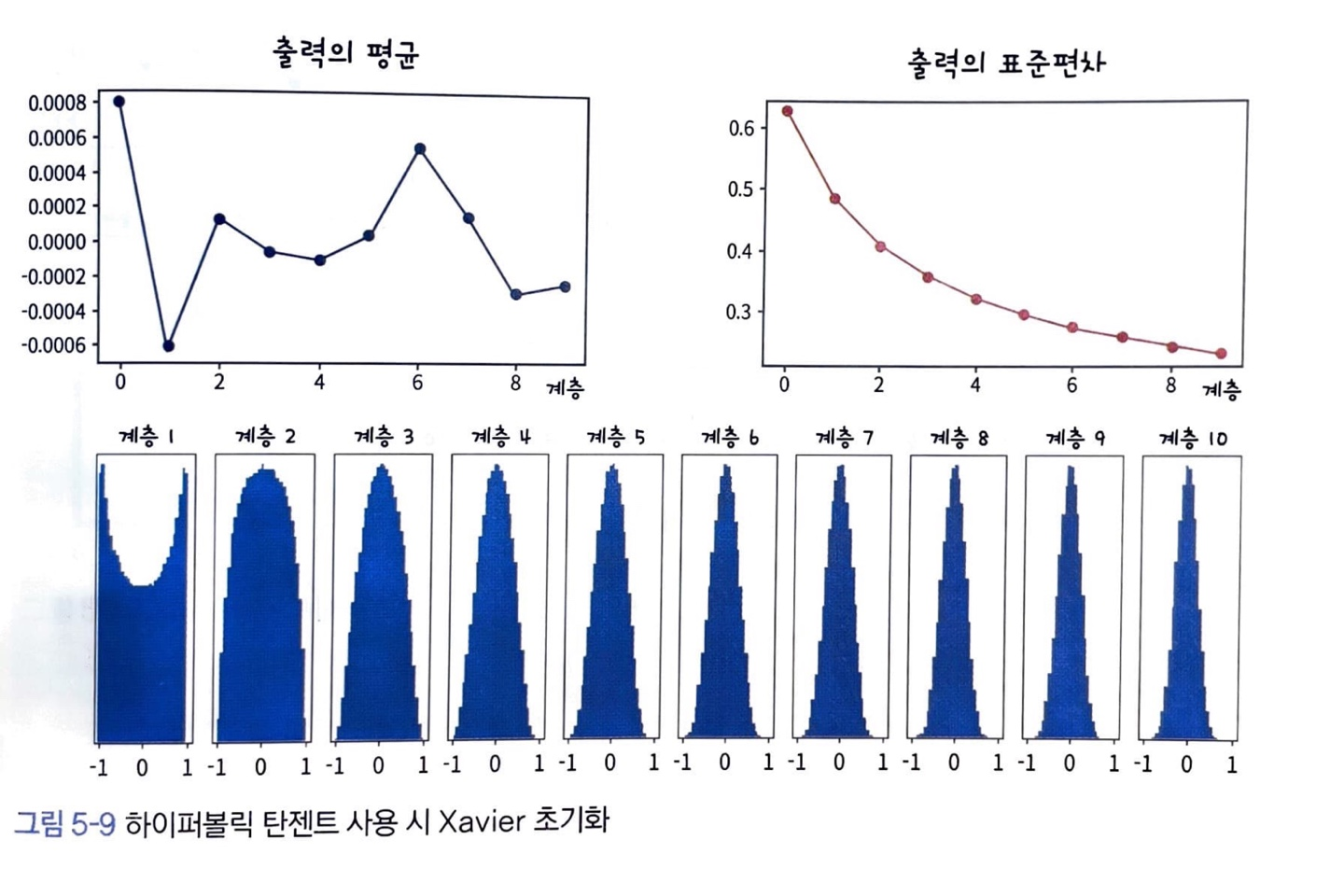
Xavier 초기화를 이용해서 신경망을 초기화 했을 경우, layer를 통과해도 분산이 잘 유지되고 있습니다.

신경망의 활성 함수가 sigmoid 계열일 때, 데이터가 분산을 유지하면서 흘러가는 Xavier 초기화를 적용하면 출력값이 0이 되거나, 1과 -1로 포화되는 현상도 사라짐

결과적으로 Gradient Vanishing이 사라져 신경망의 학습이 잘 진행됩니다.

He 초기화

활성 함수가 ReLU일 때 Xavier 초기화를 사용하면 데이터의 크기가 점점 작아집니다.

애초에 Xavier는 sigmoid 계열의 활성 함수를 사용한다는 가정하에 활성 함수를 선형 함수로 가정했기 때문인데요.

ReLU는 양수 구간에서는 가정과 동일하지만, 음수 구간에서는 맞지 않게 됩니다.

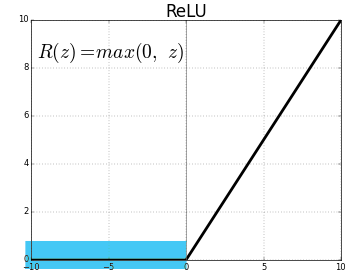
$y=0$인 구간, 파란색으로 표시된 부분이 ReLU의 비활성화 구간입니다.

분산이 절반으로 줄어들게 됩니다.

활성 함수가 ReLU일 때, Xavier 초기화를 적용해보면, 입력 데이터가 계층을 통과하면서 분산이 점점 줄어들어 출력이 0이 됩니다.

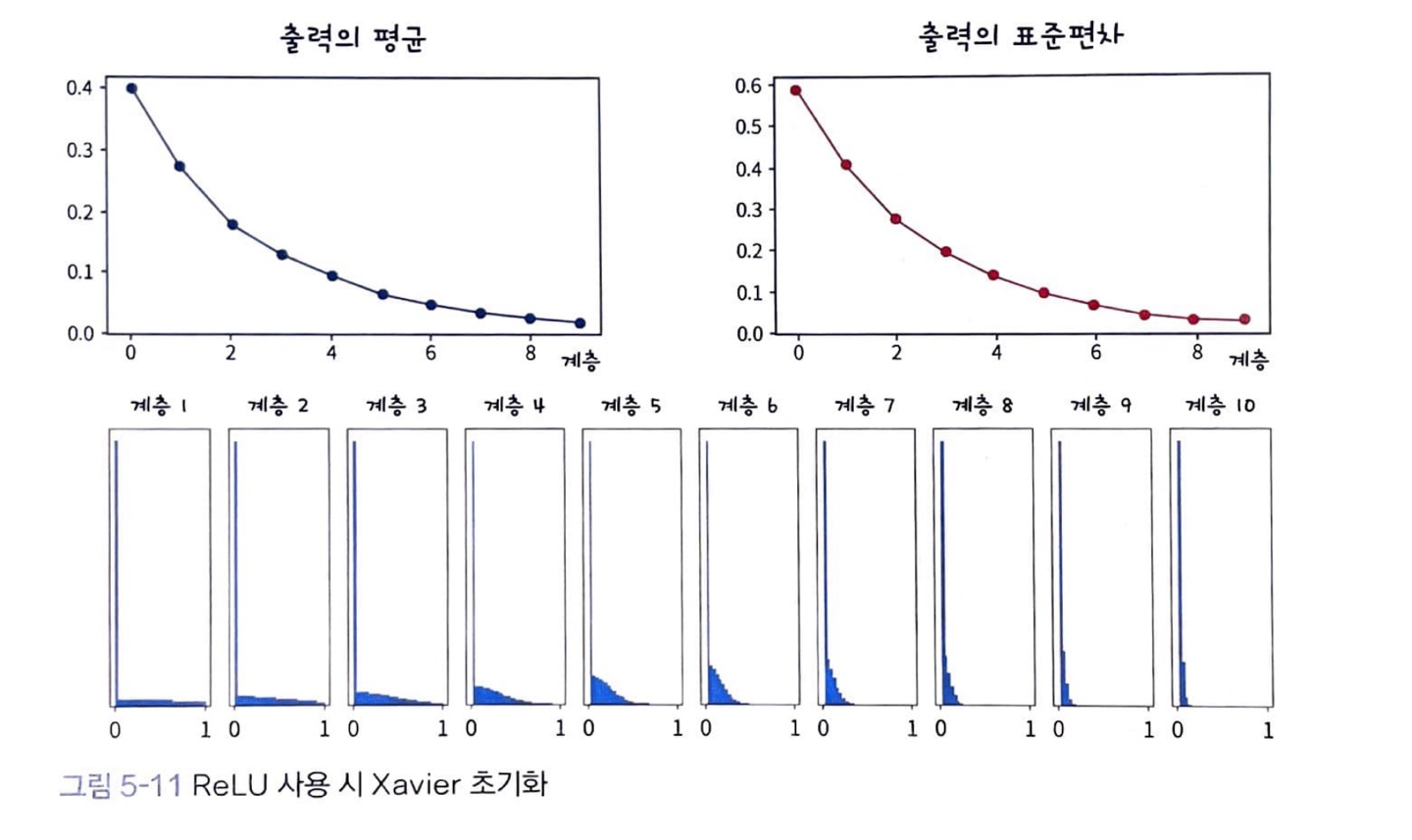
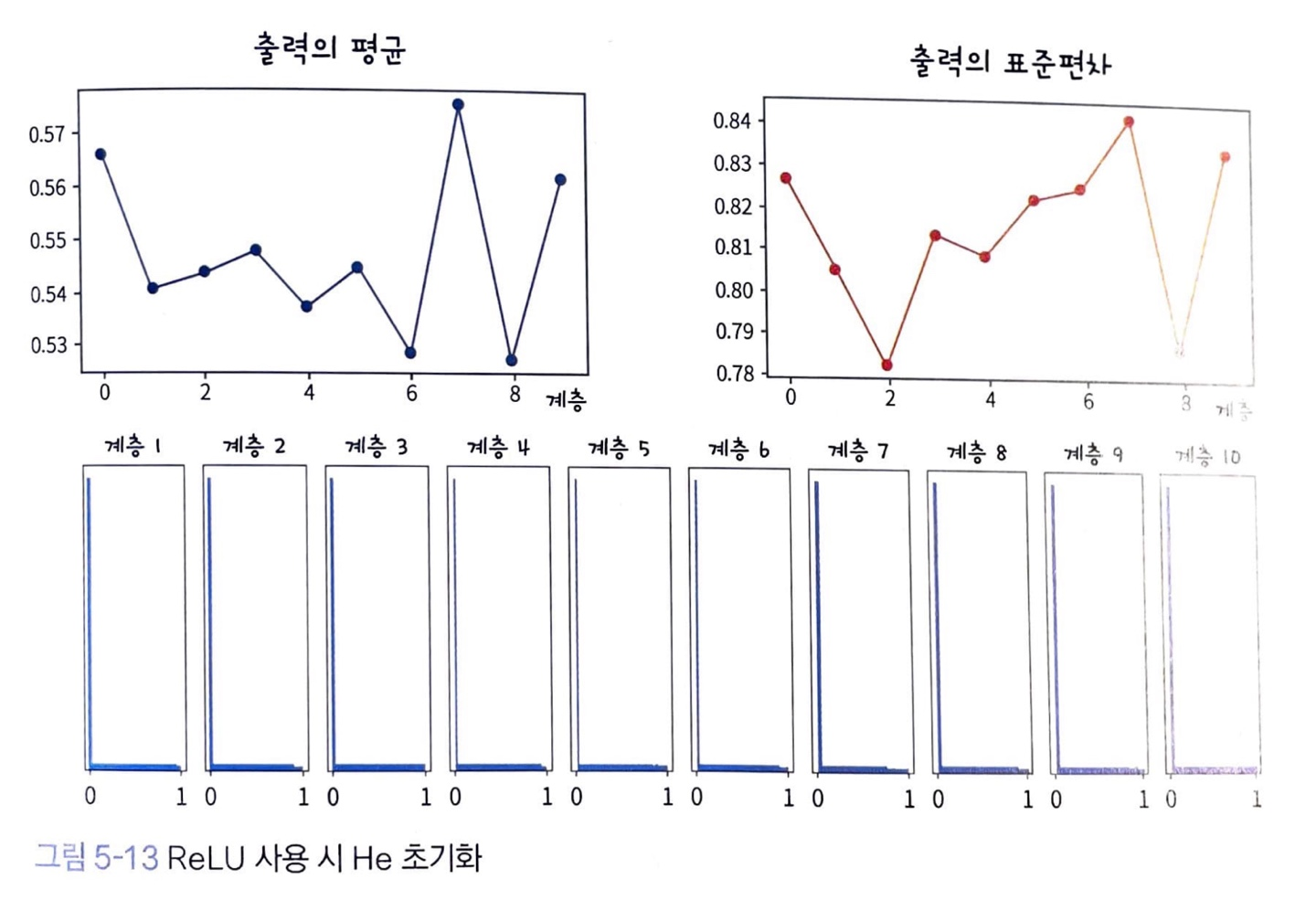
이런 한계점을 개선한 방식이 He 초기화(He Initialization)입니다.

He 초기화도 Xavier 초기화와 같이 뉴런의 입력 데이터와 출력 데이터의 분산을 같게 만들어 줍니다.

다른 점은 분산을 모델링했다는 점인데요. ReLU 사용시, 출력의 분산이 절반으로 줄어들기 때문에 가중치의 분산을 두 배로 키웁니다.

즉, Xavier 초기화는 가중치의 분산을 $1/n$로 하였다면,

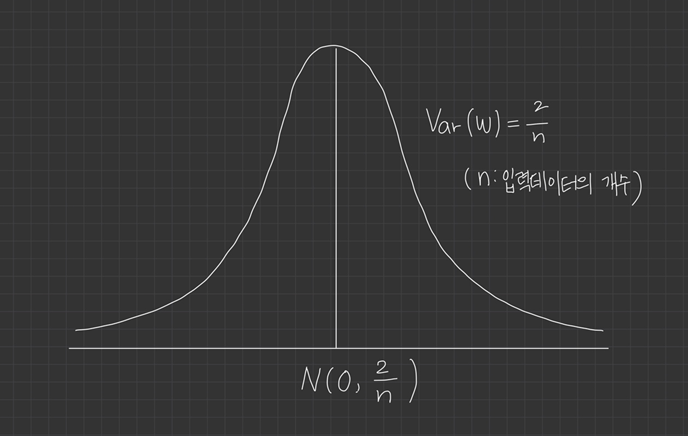
He 초기화는 가중치의 분산을 $2/n$으로 합니다.

입력 데이터가 layer들을 통과하면서 데이터의 분산이 잘 유지됩니다.

ReLU의 특성상 0에 몰려 있지만, 나머지 데이터는 양수 구간에 골고루 퍼져 있습니다.

Summary

신경망을 학습할 때 모델 초기화는 손실 함수에서 출발 위치를 결정하며, 특히 가중치 초기화는 학습 성능에 크게 영향을 미칩니다.

신경망의 가중치를 0으로 초기화하면 학습이 진행되지 않습니다.

신경망의 가중치를 0이 아닌 상수로 초기화하면 같은 계층에 있는 뉴런은 마치 하나의 뉴런만 있는 것처럼 작동합니다.

따라서 신경망의 가중치는 모두 다른 값으로 초기화해야 하며, 일반적으로 난수를 이용해서 초기화합니다.