공부 벌레가 되고 싶은 🐛 어떤 사람의 K-NN 알고리즘, 결정계수 정리 글입니다.
참고한 교재의 chapter 3-1에 해당됩니다.
참고 자료
📕 교재: 혼자 공부하는 머신러닝+딥러닝
💻 유튜브 강의: https://youtu.be/0mrLRkgbjA0
K-Nearest Neighbors
K-Nearest Neighbors을 검색하면 위키백과가 나옵니다.
📚 패턴 인식에서, k-최근접 이웃 알고리즘(또는 줄여서 k-NN)은 분류나 회귀에 사용되는 비모수 방식이다.[1]
두 경우 모두 입력이 특징 공간 내 k개의 가장 가까운 훈련 데이터로 구성되어 있다. 출력은 k-NN이 분류로 사용되었는지 또는 회귀로 사용되었는지에 따라 다르다.
- k-NN 분류에서 출력은 소속된 항목이다. 객체는 k개의 최근접 이웃 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류된다(k는 양의 정수이며 통상적으로 작은 수). 만약 k = 1 이라면 객체는 단순히 하나의 최근접 이웃의 항목에 할당된다.
- k-NN 회귀에서 출력은 객체의 특성 값이다. 이 값은 k개의 최근접 이웃이 가진 값의 평균이다.
여기서 K-NN은 분류나 회귀에 사용되는 알고리즘임을 알 수 있습니다. 분류의 경우 소속된 항목, 즉 class로 출력됩니다. 회귀의 경우는 feature 값으로 출력된다는 사실을 알 수 있습니다.
K-NN Demo
Distance Metrics(L1, L2), k의 개수에 따른 K-NN 알고리즘 변화를 볼 수 있는 데모 타입
K-NN 회귀
지도학습 알고리즘은 크게 분류와 회귀로 나뉩니다.
- 분류는 샘플을 클래스 중 하나로 분류를 하는 것
- 회귀는 클래스 중 임의의 어떤 숫자를 예측하는 것
분류의 경우, K-NN 알고리즘은 샘플에 가장 가까운 샘플 k개를 선택해서 샘플들 중 가장 다수의 표를 받은 클래스로 예측을 하게 됩니다.
회귀의 경우, K-NN 알고리즘은 분류와 똑같이 샘플에 가장 가까운 샘플 k개를 선택해서 이 샘플의 수치를 사용해 타깃을 예측합니다.
책에서는 가장 간단한 방법으로 평균을 예시로 듭니다.
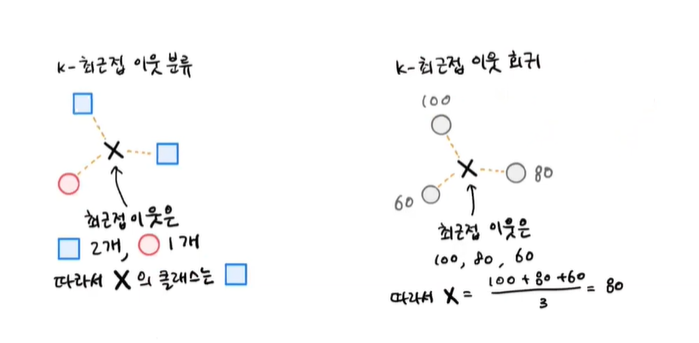
아래의 사진을 보면, 분류와 회귀의 경우 x가 3개의 sample data에 의해 어떻게 결정되는지 비교해 볼 수 있습니다.
결정계수 R
회귀에서 예측하는 값은 임의의 숫자이기 때문에 정확한 숫자를 맞추는 것은 어렵습니다.
그래서 회귀의 경우에는 다른 값으로 성능을 평가하는데 이를 결정 계수(coefficient of determination)이라 부릅니다.
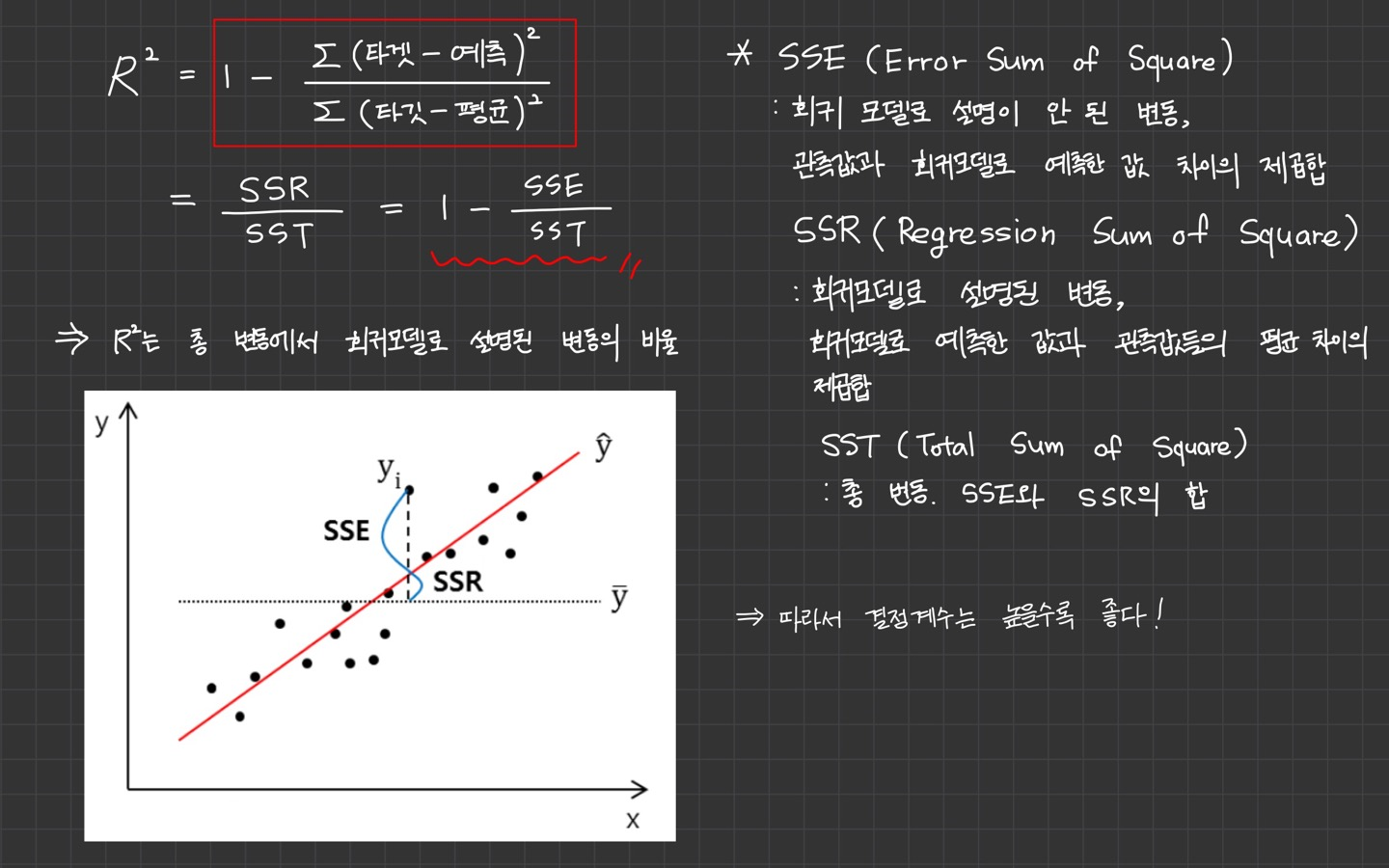
결정계수 R은 위와 같이 계산됩니다. 이해하는데 참고될만한 설명과 그래프를 덧붙여 정리해보았습니다.
overfitting, underfitting
overfitting
한 데이터셋에만 지나치게 최적화된 상태를 overfitting(오버피팅)이라고 합니다.
책에서는 train set에서는 점수가 매우 좋았는데, test set에서는 점수가 나쁜 경우를 예시를 들고 있습니다.
즉, 모델이 훈련 데이터에 너무 잘 맞지만 일반성이 떨어지는 경우를 의미합니다.
모델의 복잡도가 필요 이상으로 높기 때문이기도 한데요. 특히 train set에 noise가 너무 많거나, 데이터가 너무 적은 경우 패턴을 감지하여 학습하기 때문에 주의해야 합니다.
해결 방법으로는 train dataset을 더 모으는 것, 정규화 기법, 오류 제거, 이상치 제거 등이 있습니다.
모델의 복잡도를 더 낮추는 방법도 있습니다. 이렇게 모델을 단순하게 규제하는 것을 hyper parameter가 결정하게 됩니다.
hyper parameter는 학습 전 미리 지정되어 훈련하는 동안은 상수로 남아 있습니다. 이 규제 부분은 뒤에 나오는 것 같습니다.
underfitting
underfitting(언더피팅)은 반대의 경우에 해당됩니다.
훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 낮은 경우에 해당되는데요.
원인으로 모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못할 때 발생합니다.
해결 방법으로는 모델의 복잡도를 올리는 방법이 있습니다. K-NN의 경우 모델을 더 복잡하게 만드는 방법으로 k의 개수를 줄이는 방법이 있습니다.
이웃의 개수를 줄이면 패턴에 더 민감해지고, 이웃의 개수를 늘리면 데이터 전반에 있는 일반적 패턴을 따르게 되기 때문입니다.
또한 parameter가 더 많은 복잡한 모델을 선택하는 것, 모델의 제약을 줄이는 것(hyper parameter 값 줄이기), 조기 종료되는 (overfitting되기 전) 시점까지 충분히 학습하는 법 등이 있습니다.
