[Python] 선형 회귀 이론 및 실습

거친코딩·2021년 4월 17일

Regression numpy pandas python sklearn

기초부터 쌓아가는 머신러닝

목록 보기

5/9

기초부터 쌓아가는 머신러닝 #4

4주차 : 선형회귀 이론 및 실습

YouTube Channel(거친코딩)

- 선형 회귀란 무엇인가

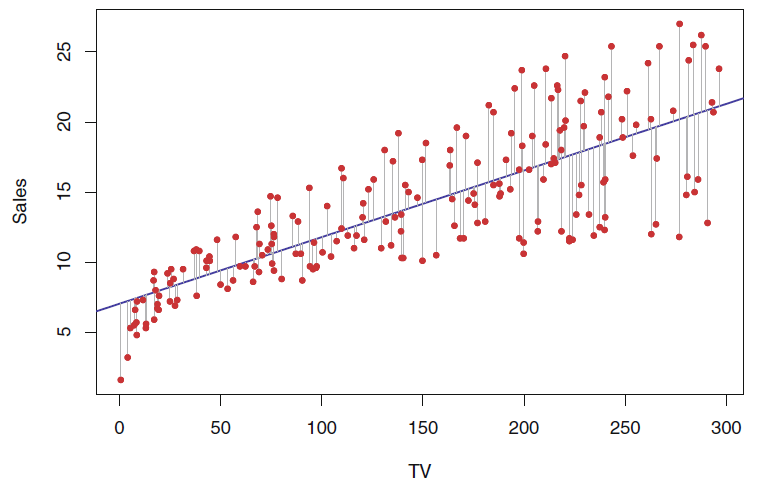
선형회귀는 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링 하는 것
연속적인 출력 값을 예측하는 것
특성이 하나인 선형 모델 공식
Y = W0 + W1*X
where W0 : y축 절편, W1 : 특성의 가중치
✔ 목적 : 특성과 타깃 사이의 관계를 나타내는 선형 방정식의 가중치(W)를 학습하는 것

- 선형 회귀 모델의 훈련과 비용함수

모델의 훈련이란
✔ 모델이 훈련 데이터에 잘 맞도록 모델 파라미터를 설정하는 것
✔ 모델이 훈련 데이터에 얼마나 잘 들어맞는지 측정해야 함
모델 훈련에 필요한 비용함수 종류

✔ MSE (Mean Squared Error)
1. 회귀 모델의 주요 손실 함수
2. 참값과 예측값의 차이인 오차들의 제곱 평균으로 정의
3. 제곱을 해주기 때문에 이상치(outlier)에 민감

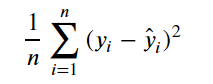
✔ MAE (Mean Absolute Error)
1. 참값과 예측값의 차이인 오차들의 절대값 평균
2. MSE보다 이상치에 덜 민감

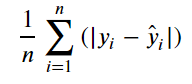
✔ RMSE (Root Mean Squared Error)
1. MSE에 root을 취해 준 것
2. 참값과 비슷한 값으로 변환하기 때문에 해석이 쉬워짐

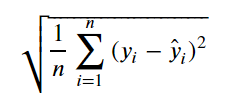
👍 보통 quadratic(2차 곡선형태) 형태의 미분 편의성이 좋기 때문에, 회귀 모형의 비용함수로 MSE를 많이 사용한다.

- 선형 회귀 모델의 최적화 방법

1.정규방정식

비용 함수를 최소화하는 θ 값을 찾기 위한 해석적 방법
정규방정식은 n개의 특성수에 따라서 (n+1) x (n+1)의 X XT 역행렬을 계산한다.
이 말은 특성의 수가 많아지면 정규방정식의 구현속도가 느려진다.
하지만 다행히도 모델의 복잡도가 훈련 세트의 샘플 수와 특성 수에 선형적으로 증가한다.
메모리 공간이 충분하다면 큰 훈련 세트도 효율적으로 처리 가능
비용함수(MSE)를 w에 대해 미분을 하면 아래와 같은 식이 나오게 된다.

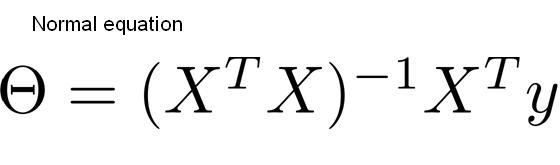
import matplotlib.pyplot as plt
import numpy as np
x = 2 * np.random.rand(100,1) # [0, 1) 범위에서 균일한 분포 100 X 1 array 
y = 4 + 3*x + np.random.randn(100,1) # normal distribution(mu=0,var=1)분포 100 X 1 array
plt.scatter(x,y)
plt.show()

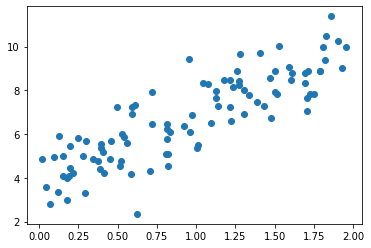
x_b = np.c_[np.ones((100,1)),x] # 모든 샘플에 index 0번에 1을 추가

# np.linalg.inv는 넘파이 선형대수 모듈(linalg)의 inv(역함수)
# .dot은 행렬 곱셈
theta_best = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y)
theta_best
> array([[ 4.93296992],
       [-0.41991499]])

기존의 목적함수가 y = 4 + 3*x + np.random.randn(100,1)라서, 예측한 θ0 : 4, θ1 : 3을 기대했지만, 비슷하긴해도 노이즈 때문에 원래의 파라미터를 맞출 수 없었다.

# theta_best를 사용해서 y 값 예측
x_new = np.array([[0],[2]])
x_new_b = np.c_[np.ones((2,1)),x_new]
prediction = x_new_b.dot(theta_best)
prediction
> array([[4.93296992],
       [4.09313993]])

plt.plot(x_new,prediction,"r-")
plt.plot(x,y,"b.")
plt.axis([0,2,0,15]) # x축 범위 0~2, y축 범위 0~15 
plt.show()

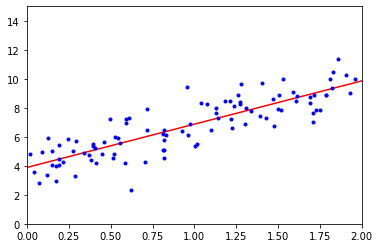
위와 같은 작업을 아래와 같이 sklearn(사이킷런) 라이브러리를 사용하여 구현할 수 있다.

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x,y)
print(lin_reg.intercept_,lin_reg.coef_)
> [3.88883297] [[2.98499978]]

print(lin_reg.predict(x_new))
>array([[3.88883297],
       [9.85883253]])

2.경사 하강법

여러 종류의 문제에서 최적의 방법을 찾을 수 있는 매우 일반적인 최적화 알고리즘
기본 메커니즘은 지정한 비용 함수를 최소화하기 위해 파라미터를 반복적으로 수정하는 것

짙은 안개 속, 앞이 전혀 보이지 않고 오로지 발 끝에 산의 기울기만 느낄 수 있다고 생각해보자. 이 숲을 벗어나기 위한 가장 좋은 방법은 가장 기울기가 급한 길을 따라서 내려가는 것이다. 이것이 경사 하강법 원리다.
무작위로 벡터 θ를 초기화한다.
파라미터 벡터 θ에 대해 비용 함수(Loss Function)의 현재 그래디언트를 계산한다.
그리고 그래디언트가 감소하는 방향으로 진행하면서, 최종적으로 계산된 그래디언트가 0이 되면 최솟값에 도달하도록 해야 한다.
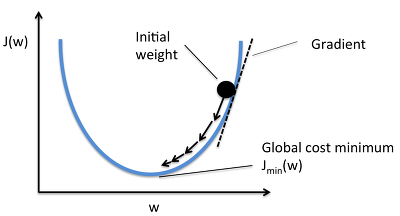
위 그림처럼 경사 하강법에서 최적화 시키는 방향으로 가게 하는 중요한 하이퍼파라미터 step(learning rate)를 결정해야 한다.
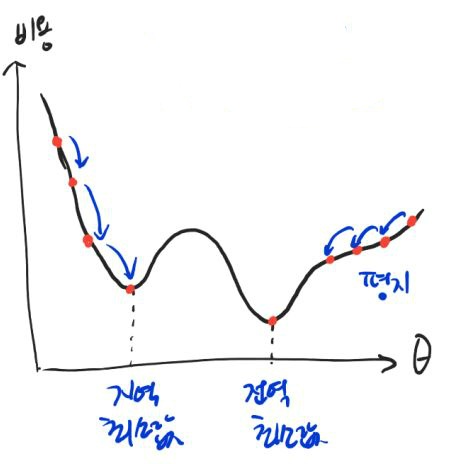
실제 모든 비용함수는 위와 같이 quadratic(이차원)하게 표현되지 않고 울긋불긋하게 솟았다가 내려앉았다가 한다.
학습률이 너무 작은 경우에는 local minumum(지역 최소값)에 빠지게 된다.
학습률이 너무 큰 경우에는 수렴이 되지 않게 된다.
그래서 위 그림처럼 학습률을 잘 조정해야지, global minumum(최적의 값)으로 잘 수렴할 수 있다.
다행히도 선형 회귀의 MSE 비용 함수는 convex function(볼록 함수)이기 때문에, local minum이 없고, global minimum만 존재한다.
그래서 충분한 시간과 적절한 학습률만 주어진다면, global minimum에 최대한 근접할 수 있다.
위 그림처럼 오른쪽의 경사 하강법은 곧장 global minimum으로 내려갈 수 있다.
왼쪽의 그림에서 완만한 경사를 만나게 되면 global minimum으로 내려갈 수는 있지만 더 오래 걸린다.
경사 하강법 전에는 반드시 모든 특성을 같은 스케일을 사용하여서 데이터 변환을 하여야 한다.
scikit learn(사이킷런) 라이브러리에서 각 특성에서 평균을 빼고 표준편차로 나누어 평균을 0 분산을 1로만드는 StandardScaler을 사용하곤 한다.

✔ 배치 경사 하강법

경사 하강법에서 각 모델의 θj에 대한 비용 함수의 partial derivative(편미분) 값을 1번 처럼 계산해야 한다.
partial derivative를 각각 계산하는 대신 2번처럼 한번에 계산도 가능하다.
위 공식은 매 경사 하강 스텝에서 전체 훈련 세트에 대해 계산한다.
그래서 이 공식을 Batch Gradient Descent(배치 경사 하강법)이라고 한다.
전체 데이터를 다 사용하기 때문에 큰 훈련 세트에서는 아주 느리다.
🎈 장점으로는, 특성 수에 민감하지 않기 때문에 정규방정식보다 경사 하강법을 사용하는 것이 훨씬 빠르다.
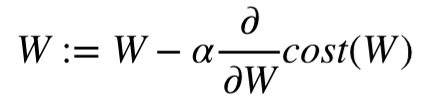
위와 같이 그래디언트 벡터가 계산되면 학습률(alpha)에 그래디언트 벡터를 곱하고 이전 weight에 빼면 된다.

# 경사 하강법 구현(implementation)
import numpy as np

x = 2 * np.random.rand(100,1) # 100 x 1 크기의 0~1의 균일분포 
x_b = np.c_[np.ones((100,1)),x] # bias(1)를 전체 데이터에 추가 
y = 4 + 3*np.random.randn(100,1) # 100 x 1 크기의 표준정규분포 추출

learning_rate = 0.001
iterations = 1000
m = x_b.shape[0] # 100개 (x 데이터)

theta = np.random.randn(2,1) # 2x1 크기의 평균 0, 분산1 정규 분포 추출

for iteration in range(iterations):
  gradients = 2/m * x_b.T.dot(x_b.dot(theta)-y)
  theta = theta - (learning_rate * gradients)


# 정규방정식으로 찾은 것과 정확히 일치한다.
theta
> array([[ 4.93296992],
       [-0.41991499]])

✔ 확률적 경사 하강법

앞서, 배치 경사 하강법에서 언급한대로 매 스텝에서 전체 훈련 세트를 사용해서 그래디언트를 계산해야 하는 큰 문제가 있다.
이러한 문제를 극복하기 위해, 확률적 경사 하강법은 매 스텝마다 한 개의 샘플을 무작위로 선택 및 그 샘플에 대한 그래디언트를 계산한다.
매 반복에서 적은 양의 데이터로 그래디언트를 계산하고 업데이트 하기 때문에 최적화가 더 빠르다.
그리고 전체 데이터에서 샘플을 추출해서 최적화 시키기 때문에 매우 큰 훈련 데이터 역시 처리할 수 있다.
하지만 무작위 추출이기 때문에, 전체 데이터를 사용하는 것 보다 안정적이지는 못하다.
위 그림과 같이 비용 함수의 global minumum에 도달하기 까지 요동치며 평균적으로 감소한다.
요동치면서 최적의 해에 가까워지기는 하겠지만, 최소값에 도달하지 않을 수도 있다.
하지만 비용 함수가 MSE처럼 convex(볼록 함수)하지 않고 불균형하다면 배치 경사 하강법보다 global minimum에 도달할 가능성이 높다.
무작위성으로 인한 global minimum에 도달하지 않을 수 있다는 단점을 극복하기 위해서, 학습률을 점진적으로 감소시키는 해결책이 있다.(시작: 학습률 크게 => 진행단계: 학슬률 작게)
위 해결책을 위한 매 반복 학습률 결정 함수를 learning schedule(학습 스케쥴)이라고 부른다.

# 확률적 경사 하강법 구현(implementation)
epochs = 1000
t0,t1 = 5,50 # 학습 스케쥴 (하이퍼 파라미터)
m = x_b.shape[0] # 100개 (x 데이터)

def learning_schedule(t):
  return t0 / (t+t1)

theta = np.random.randn(2,1) # 2x1 크기의 평균 0, 분산1 정규 분포 추출

for epoch in range(epochs):
  for i in range(m):
    random_index = np.random.randint(m) # 0 ~ m-1까지 랜덤 숫자 1
    xi = x_b[random_index:random_index:+1] # 1 x 2 크기
    yi = y[random_index:random_index+1] # 1 x 1 크기
    gradients = 2 * xi.T.dot(xi.dot(theta)-yi) # 1 => mini_m
    learning_rate = learning_schedule(epoch*m + i)
    theta = theta - learning_rate * gradients

✔ 미니배치 경사 하강법

미니배치는 위 배치와 확률적 경사 하강법을 안다면 이해하기 쉽습니다.
각 Step에서 전체 훈련 세트를 일일이 다 학습하는 배치 경사 하강법이나 훈련 세트의 하나의 샘플을 통해서 학습하는 확률적 경사 하강법과 같이 그래디언트를 계산하는게 아니라, Mini Batch라 부르는 임의의 작은 샘플 세트에 대해 그래디언트를 계산하는 것이다.
확률적 경사 하강법에 비해 행렬 연산에 최적화된 GPU를 사용해서 성능을 더 올릴 수 있다.
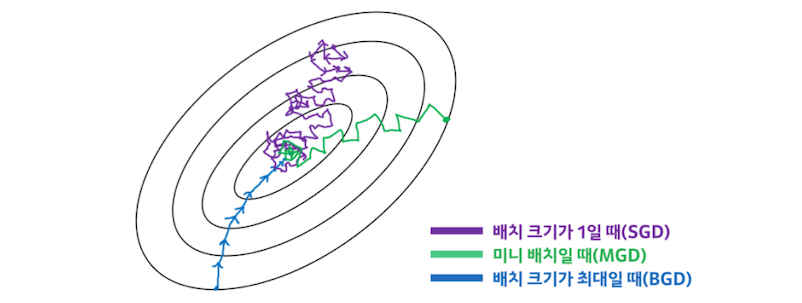
미니 배치가 큰 경우, 파라미터 공간에서 SGD(확률적 경사 하강법)보다 덜 불규칙하게 움직인다.
곧, SGD보다 최소값에 도달할 수 있는 가능성이 더 높지만, Local Minimum(국소값)에 빠질 위험은 존재한다.

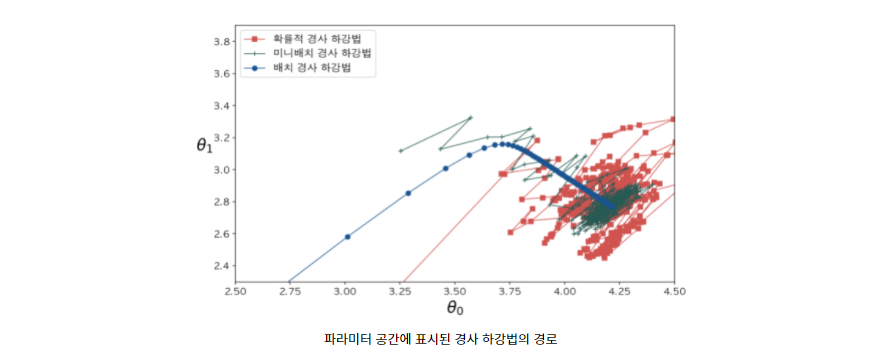
위 그림은 국소값이 많고 문제가 되는 파라미터 공간에서 배치, 미니배치, 확률적 경사 하강법을 비교한 그림이다.
모두 최소값에 도달하였지만, 배치 경사 하강법이 실제 최소값에서 도달하였고, 나머지 두 방법은 근처를 맴돌고 있다.
배치 경사 하강법이 최소값에 도달할 수는 있지만, 매 스텝에서 많은 시간과 비용이 든다.
확률적 경사 하강법과 미니 배치는 적절히 학습 스케쥴을 사용한다면 최소값에 마찬가지로 도달 할 수 있다.

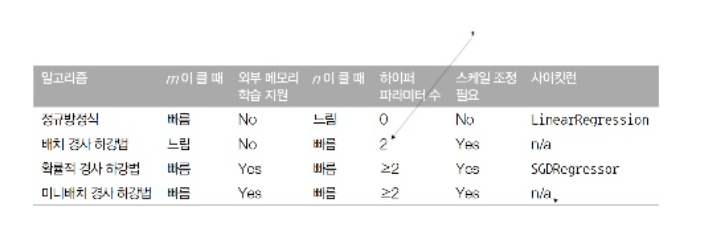
사이킷런의 SGDRegressor와 SGDClassifier에서 partial_fit 메서드를 사용하여 모델 파라미터를 초기화하지 않고 미니배치 학습을 위해 반복적으로 호출할 수 있다. 하지만 partial_fit 메서드는 fit 메서드와 동일하게 미니배치의 샘플을 하나씩 적용하므로 엄밀히 말하면 미니배치 경사 하강법 알고리즘은 아니다. - 핸즈온 머신러닝 -

- 다항 회귀

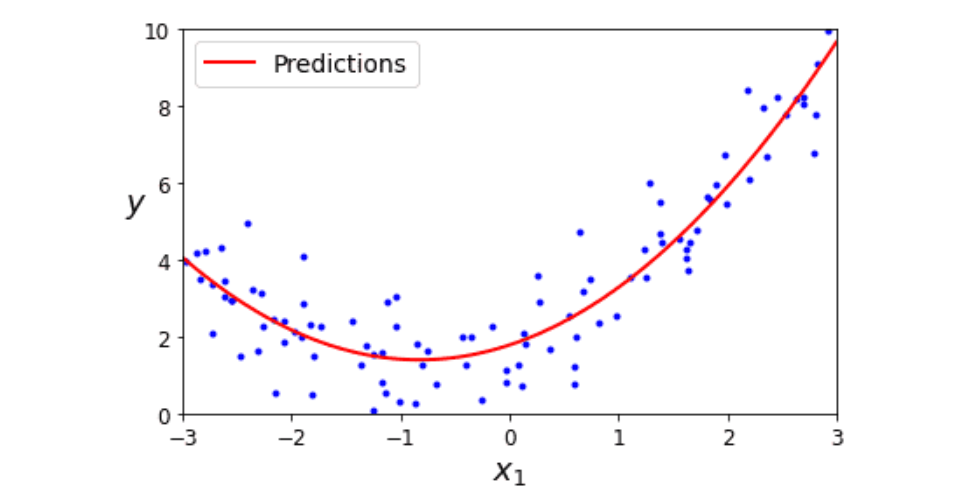
비선형성을 띄는 데이터도 선형 모델을 활용하여서 학습시킬 수 있다.
기존 특성에다가 log, exp, 제곱 등과 같은 basis function을 적용하여, 확장된 특성을 포함한 형태로 변형한 뒤 학습시키는 것을 다항 회귀 기법이라고 한다.
위와 같은 예시를 2차 방정식으로 간단하게 들어 보겠다.

import numpy as np
data_num = 1000
x = 3 * np.random.rand(data_num,1) - 1
y = 0.2 * (x**2) + np.random.randn(1000,1)

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2,include_bias=False)
x_poly = poly_features.fit_transform(x)
print(x[0])
print(x_poly[0])
>[0.35316774]
>[0.35316774 0.12472745]

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x_poly,y)
print(lin_reg.intercept_,lin_reg.coef_)
>[-0.0427474] [[-0.05998741  0.25104612]]

예측 모델의 식은 y_hat = 0.25x^2 - 0.05x^1 + 1 이다. 실제 원래 홤수와 거의 비슷해졌다.
특성이 여러 개 일 때 다항 회귀는 이 특성 사이의 관계를 찾을 수 있습니다.(PolynomialFeatures를 통해서 주어진 차수까지 특성 간의 모든 교차항을 추가할 수 있기 때문)
훈련 세트와 검증 세트의 모델 성능을 살펴 보는 것, (모델 과적합을 가시적으로 확인 하는 법)

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

def plot_learning_curves(model,x,y):
  x_train,x_val,y_train,y_val = train_test_split(x,y,test_size=0.2)
  train_errors,val_errors = [],[]
  for num in range(1,len(x_train)):
    model.fit(x_train[:num],y_train[:num])
    y_train_predict = model.predict(x_train[:num])
    y_val_predict = model.predict(x_val)
    train_errors.append(mean_squared_error(y_train[:num],y_train_predict))
    val_errors.append(mean_squared_error(y_val,y_val_predict))
  plt.plot(np.sqrt(train_errors),'r-+',linewidth=2,label='train_set')
  plt.plot(np.sqrt(val_errors),'b-',linewidth=3,label='val_set')   
  plt.legend()
  plt.show()

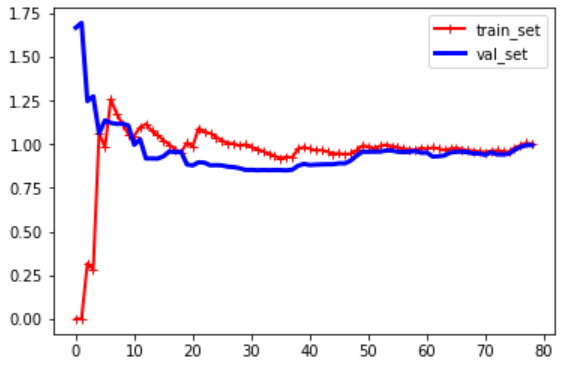
basis function(4차 다항식)과 모델을 파이프라인을 거쳐서 바로 모델링 및 평가하는 법

from sklearn.pipeline import Pipeline
data_num = 100
x = 3 * np.random.rand(data_num,1) - 1
y = 0.2 * x**2 + np.random.randn(100,1)
polynomial_regression = Pipeline([
  ("poly_features",PolynomialFeatures(degree=4,include_bias=False)),
  ("lin_reg",LinearRegression())
  ])
plot_learning_curves(polynomial_regression,x,y)

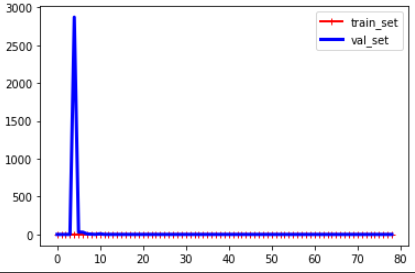
- 규제가 있는 선형 모델

앞에서도 보았듯이 과대적합을 감소시키는 것이 아주 중요하고, 그 과대적합을 줄일 수 있는 방법을 강구해야 한다.
그 방법 중 loss에 새로운 term을 추가하여서 모델 weight에 대한 규제를 가하는 것이다.

Lasso Regression (라쏘 회귀)
- Lasso(라쏘)회귀는 선형 회귀의 규제된 버전이다.
- 비용 함수에 L1 term(가중치에 절대값을 적용한 형태)을 사용하여서 weight에 규제를 한다.

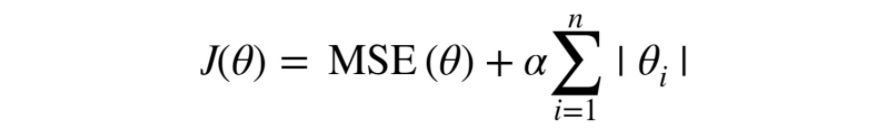
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(x,y)
lasso_reg.predict([[1.5]])
>array([0.22365566])

Ridge Regression (릿지 회귀)
- Ridge(릿지)회귀는 선형 회귀의 규제된 버전이다.
- 비용 함수에 L2 term(가중치에 제곱을 한 형태)을 사용하여 weight에 규제를 한다.

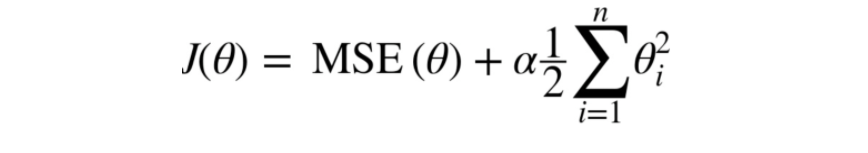
# 안드레 루이 숄레스키가 발견한 행렬 분해(matrix factorization) 사용
# 숄레스키 분해의 장점은 성능이다. 원래 ridge의 solver default값은 'auto'이며 희소 행렬이나 특이 행렬이 아니면 'cholesky'가 된다.
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.1,solver='cholesky')
ridge_reg.fit(x,y)
ridge_reg.predict([[1.5]])
>array([[0.29217567]])

Elastic Net Regression (엘라스틱넷 회귀)

Elastic Net(엘라스틱넷)은 릿지 회귀와 라쏘 회귀를 합성한 모델이다.
규제 term은 릿지회귀의 규제term과 단순히 더해서 사용하고, 혼합 비율 r을 조절해서 사용한다.
r=0이면, 엘라스틱 넷은 => 릿지 회귀
r=1이면, 엘라스틱 넷은 => 라쏘 회귀

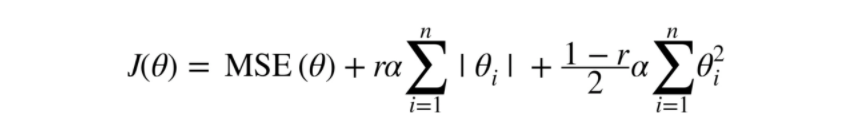
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1,l1_ratio=0.5)
elastic_net.fit(x,y)
elastic_net.predict([[1.5]])
>array([0.23234511])

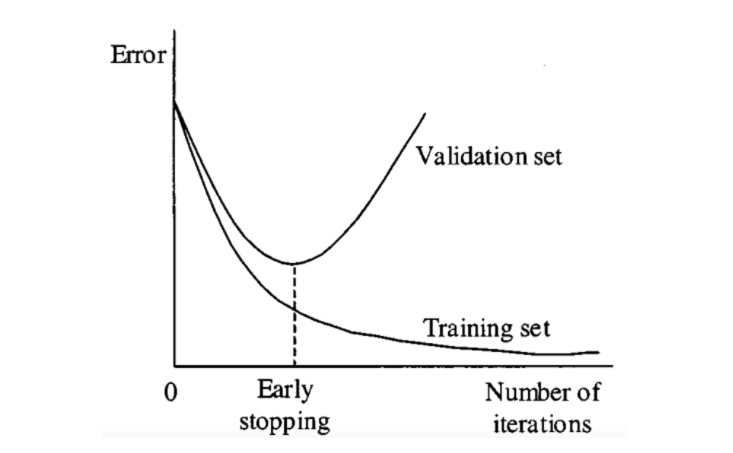
- Early Stopping (조기 종료)

경사 하강법과 같은 반복적인 학습 알고리즘을 규제하는 것은 실제 비용함수에 규제항을 추가하는 것 뿐만 아니라, 검증 에러가 훈련 에러에 비해 치솟게 되면 바로 훈련을 중지시키는 방법도 있다. 이를 early stopping이라 한다.

from sklearn.base import clone
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.linear_model import SGDRegressor
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error

x = 3 * np.random.rand(data_num,1) - 1
y = 0.2 * x**2 + np.random.randn(100,1)

poly_scaler = Pipeline([
                        ("poly_features",PolynomialFeatures(degree=90,include_bias=False)),
                        ('std_scaler',StandardScaler())
])

x_train,x_val,y_train,y_val = train_test_split(x,y,test_size=0.2)
x_train_poly_scaled = poly_scaler.fit_transform(x_train)
x_val_poly_scaled = poly_scaler.transform(x_val)

# warm_start=True 이면 fit 메서드가 호출될 때 처음부터 다시 하지 않고 이전 모델 파라미터에서 훈련 이어짐
# penalty : {‘l2’, ‘l1’, ‘elasticnet’}, default=’l2’
# n_iter_no_change : Number of iterations with no improvement to wait before stopping fitting
# 'constant' : eta = eta0
# 'optimal' : eta = 1.0 / (alpha * (t + t0))
# 'invscaling' : eta = eta0 / pow(t, power_t)
# 'adaptive' : eta = eta0, as long as the training keeps decreasing
sgd_reg = SGDRegressor(n_iter_no_change=1,warm_start=True,penalty=None,
                       learning_rate='constant',eta0=0.0005)
SGDRegressor()
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000):
  sgd_reg.fit(x_train_poly_scaled,y_train.ravel())
  y_val_predict = sgd_reg.predict(x_val_poly_scaled)
  val_error = mean_squared_error(y_val,y_val_predict)
  if val_error<minimum_val_error:
    minimum_val_error = val_error
    best_epoch = epoch
    best_model = clone(sgd_reg)
print('best_epoch : ',best_epoch)
print('best_model : ',best_model)