
데이콘에서 피처(feature)가 4000개가 넘는 대회에 나갔다가 "아, 차원 축소도 고려해볼 걸!"이라는 후회가 들어서 공부해보려고 합니다.
다음 대회 혹은, 프로젝트에서 차원 축소를 사용해 볼 기회가 왔을 때 응용할 수 있으면 좋겠다는 마음에 글을 써봅니다.
피드백은 언제나 환영입니다😊
참고로 수학적 기법은 거의 설명하지 않으며 coding으로 구현하는 로직에 특화되어있습니다.
차원 축소(Dimensionality Reduction)
1. 차원 축소(Dimensionality Reduction)란?
머신러닝을 하다보면(특히, Traditional ML) 피처 개수가 수십개에서 많으면 수천개가 되는 경우를 볼 수 있습니다.
우리는 이런 경우 모델의 성능이 떨어질 것으로 예상해 차원 축소라는 기법을 사용합니다.
차원 축소 방식에는 기존 데이터에서 필요한 데이터만 추출하는 Feature Selection, 기존 데이터를 이용해 새로운 축(axis)을 만들어 저차원으로 만드는 Feature Extraction 방식이 있습니다.
Feature Selection방식은 EDA를 통해 데이터를 이해하고 데이터를 선택하는 방식입니다.
Feature Selection은 개념적으로 중요한 것보다 실무, 대회 등 실전에서 어떤 데이터를 만나는가에 따라 피처 중요도의 기준이 달라질 수 있습니다.
Feature Extraction방식은 고차원 데이터를 조합하여 새로운 저차원 데이터로 표현하는 방식입니다.

2. 차원 축소(Dimensionality Reduction)를 왜 써야하는가?
앞서 피처 개수가 많아져 모델의 성능이 떨어진다고 말씀드렸습니다.
그렇다면 왜 피처 개수가 많아지면 모델 성능이 떨어질까요?
정확히 말하면 피처 개수가 많아짐에 따라 모델 성능이 무조건적으로 떨어지는 것은 아니고 "피처 개수가 많아짐에 따라 데이터들간의 거리가 멀어져 모델 성능을 신뢰할 수 없게 된다"라는 말이 더 정확합니다.
피처 개수가 많아져 고차원이 되면 희소 데이터(sparse data)가 되기 쉬운데 머신러닝 모델의 경우 희소 데이터에서 learning이 잘 되지 않을 수 있습니다.(특히, 거리 기반의 알고리즘)
차원의 저주라고도 불리는 데이터 희소성 문제를 해결하는 방법은 대표적으로 Feature Selection, Feature Extraction기법이 있습니다.
이후 소개하는 모든 차원 축소 방식은 Feature Extraction방식입니다.
3. PCA
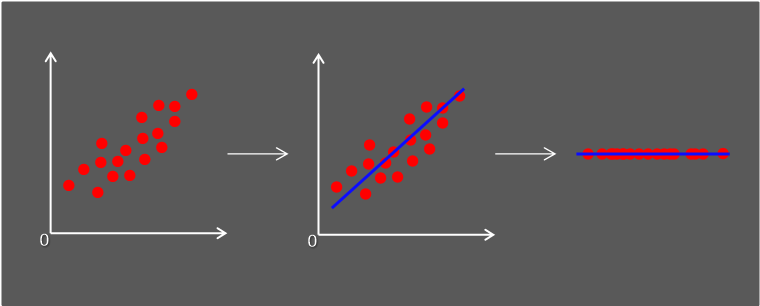
PCA(Principal Component Analysis)는 고차원 데이터와 가장 비슷하면서 더 낮은 차원을 찾아내는 비지도 학습 방법입니다. 주성분 분석이라고도 부릅니다.
PCA는 많이 쓰이는 Feature Extraction방식입니다.
PCA의 특징은 최대한 원본 데이터의 분산을 최대한 유지하는 것입니다.
sklearn의 iris 데이터를 이용해 sepal length와 sepal width feature사이에서 분포가 어떻게 되어있는지 확인해보겠습니다.
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import numpy as np
import pandas as pd
import seaborn as sns
iris_data = load_iris()
iris_df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
iris_df['target'] = iris_data.target
sns.scatterplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='target')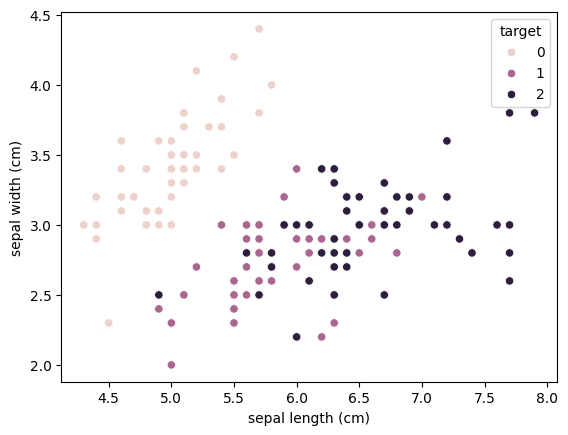
target이 0인 값에 대해서는 이미 분류가 잘 되어있음을 볼 수 있습니다.
iris데이터는 4개의 피처를 가지고 있는데 여기서 PCA를 이용해 2개로 차원 축소를 한 후 다시 시각화를 해보겠습니다.
pca = PCA(n_components=2)
pca_iris_data = pca.fit_transform(iris_data.data)
pca_iris_data_df = pd.DataFrame(pca_iris_data, columns=['component_1', 'component_2'])
pca_iris_data_df['target'] = iris_data.target
sns.scatterplot(data=pca_iris_data_df, x='component_1', y='component_2', hue='target')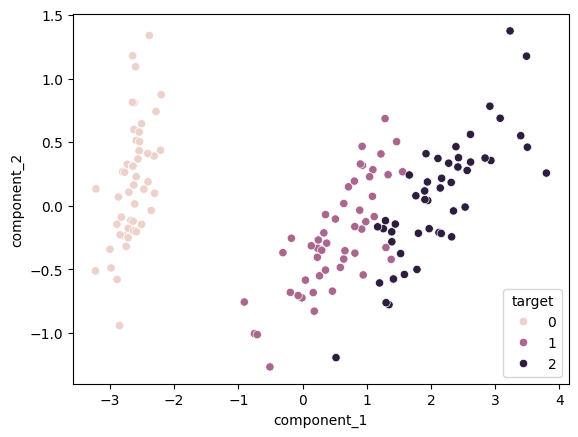
PCA를 적용하니 타겟 값에 따라 잘 분리된 것을 볼 수 있습니다.
하지만 그렇다고해서 분류 모델에서 성능이 더 좋아지는 것은 아닙니다.
기존에는 4개의 피처를 가지는 상태에서 2개만 본 것이므로 실제 4차원인 데이터셋을 일부 피처만 가지고 온 것과 비교한 것이기 때문입니다.
pca.explained_variance_ratio_
pca의 속성 'explainedvariance_ratio'을 살펴보면 2개의 피처만으로 원본 데이터의 97%의 방향성을 가짐을 알 수 있습니다.
4. LDA
선형판별분석법이라고도 불리는 LDA(Linear Discriminant Analysis)는 PCA와 마찬가지로 고차원 데이터를 저차원 축에 투영시키는 방식이지만, 그 방식에 차이가 있습니다.
PCA는 원본데이터의 방향성이 최대한 훼손되지 않도록 즉, 데이터 정보의 손실을 최소화하며 저차원으로 투영시키는 것이 목적이었습니다.
LDA는 원본데이터에서 target을 기반으로 잘 '분류'할 수 있는지가 목적이 됩니다.
다시말해, 클래스 분리를 최대화하며 클래스 내부 분산을 최소화하는 방향성을 가지는 차원 축소 방식입니다.
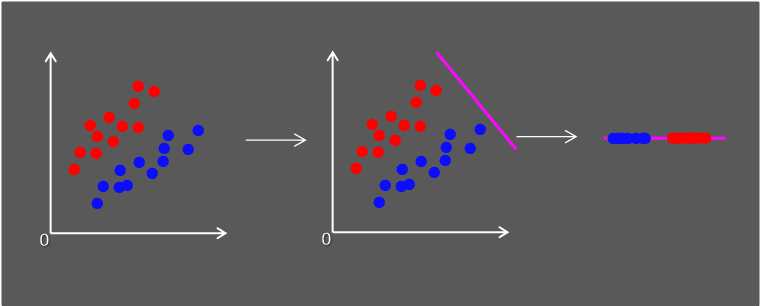
앞에서 LDA는 target을 기반으로 잘 '분류'한다는 기준을 가진다고 했죠?
따라서 LDA는 분류 알고리즘입니다.
위에서 만든 iris data를 이용해 LDA를 적용한 후 시각화 해보겠습니다.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda_iris_data = lda.fit_transform(iris_data.data, iris_data.target)
lda_iris_data_df = pd.DataFrame(lda_iris_data, columns=['lda_component_1', 'lda_component_2'])
lda_iris_data_df['target'] = iris_data.target
sns.scatterplot(data=lda_iris_data_df, x='lda_component_1', y='lda_component_2', hue='target')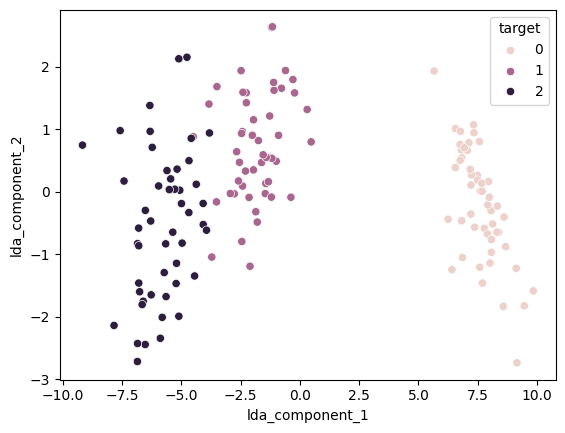
target 0은 원본 데이터에서도 잘 분리가 되어있었기 때문에 그렇다치지만 target 1과 2는 PCA와 비교했을 때 더 잘 분리된 것이 보입니다.
따라서 LDA는 분류 모델(RandomForest, DecisionTree, SVM 등)의 성능을 향상시키거나 피처가 너무 많은 경우 사용됩니다.
5. SVD
특이값 분해라고도 불리는 SVD(Singular Value Decomposition)는 m x n차원의 행렬에 대해 고유값 분해가 가능하게 해줍니다.
기존 PCA방식은 정방행렬에 대해서만 고유값 분해가 가능했지만, SVD는 정방행렬이 아니어도 고유값 분해가 가능합니다. 또한 희소행렬에도 적용이 가능합니다.
SVD방식에는 Full SVD, Compact SVD, Truncated SVD 방식이 있습니다.
- Full SVD
Full SVD방식은 차원 축소 시 잘 쓰이지 않지만 Compact SVD와 Truncated SVD의 기본이 됩니다.
SVD는 어떤 m x n행렬 A가 있을 때 다음처럼 행렬을 분해할 수 있다는 '행렬분해'방법입니다.
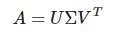
이렇게 분해된 각 행렬은 m x m, m x n, n x n크기를 가집니다.
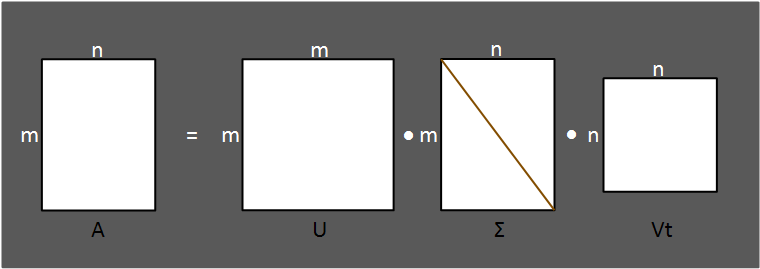
하지만 차원 축소를 할 때 Full SVD는 잘 사용하지 않습니다.
- Compact SVD
특이값 분해(SVD)에서 행렬 A를 분해하면 Sigma가 나오게 된다고 설명했습니다.
이때 Sigma는 대각행렬입니다.
만약 행렬 A가 서로가 의존적인 피처들을 가지고 있다면 Sigma의 대각선 상에 위치한 원소들 중 0으로 바뀌는 경우가 생기게 됩니다.
이때 Sigma가 0인 부분을 제거해 행렬분해를 더 Compact하게 만들어 주는 것이 Compact SVD입니다.
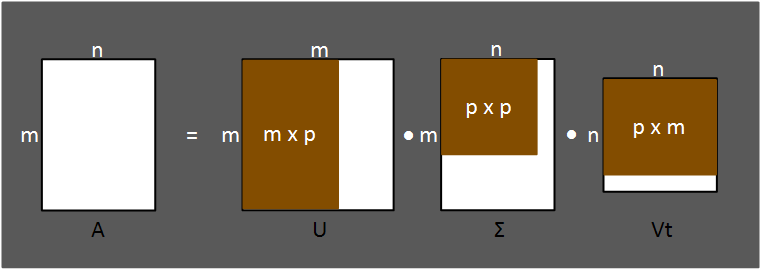
scipy 모듈은 SVD연산을 지원합니다.
이를 통해 Compact SVD대해 좀 더 이해해 보겠습니다.
다음은 서로 종속적인 행렬을 임의로 만들어 Sigma를 구해보는 과정입니다.
import numpy as np
from scipy.linalg import svd
# 서로 의존적인 행이 존재하는 4X4 행렬 만들기
np.random.seed(0)
array = np.random.randn(4, 4)
array[0] = array[1] + array[2]
array[3] = array[0]
U, Sigma, Vt = svd(array)
print(Sigma)
결과를 보면 Sigma의 대각원소가 0인 부분(엄밀히는 0에 근접)이 있음을 알 수 있고 이 부분을 잘라 Compact하게 행렬을 쪼갤 수 있습니다.
- Truncated SVD
여기서 더 들어가 특이값 중 상위에 있는 대각 원소만 선택하여 원하는 크기의 행렬로 분해하는 방식을 Truncated SVD라고 합니다.
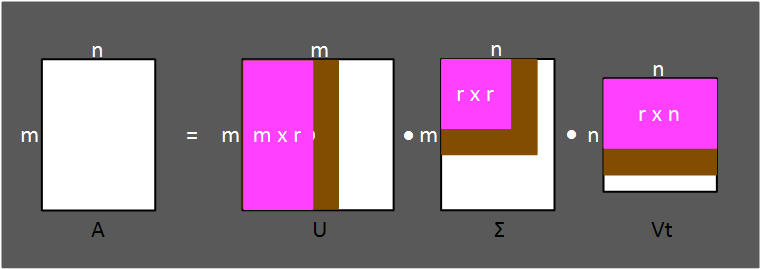
Truncated SVD방식을 사용하면 차원을 축소하는데는 효율적이지만 원본 데이터를 온전히 유지하지는 못합니다.
이는 noise 값을 없애는 장점이 될 수도 있고, essential 값을 없애는 단점이 될 수도 있습니다.
sklearn에서는 Truncated SVD를 이용한 차원 축소를 지원합니다.
import numpy as np
from scipy.linalg import svd
from sklearn.decomposition import TruncatedSVD
# 4X4 테스트 행렬 만들기.
np.random.seed(0)
array = np.random.randn(4, 4)
# scipy의 svd를 이용해 U, Sigma, Vt 구하기
U, Sigma, Vt = svd(array)
Sigma = np.diag(Sigma)
cust_svd_array = np.dot(U[:, :2], Sigma[:2, :2])
# truncated svd기법을 이용해 차원 축소
svd = TruncatedSVD(n_components=2)
svd_array = svd.fit_transform(array)저는 scipy의 svd를 이용해 직접 행렬을 구해 다시 계산해 차원 축소를 진행한 cust_svd_array와 sklearn의 svd_array의 차이를 비교해봤습니다.
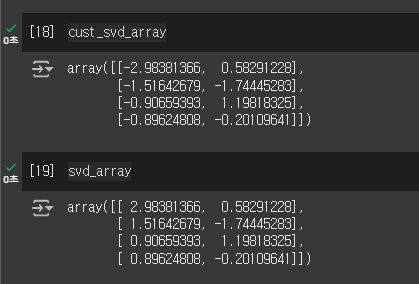
당연하게도 결과는 같았습니다.
간단하게 iris데이터에 Truncated SVD를 적용하고 시각화 해보았습니다.
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import TruncatedSVD
import numpy as np
import pandas as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
iris_data = load_iris()
iris_df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
iris_df['target'] = iris_data.target
scaler = StandardScaler()
iris_df.iloc[:, :-1] = scaler.fit_transform(iris_df.iloc[:, :-1])
svd = TruncatedSVD(n_components=2)
svd_iris_data = svd.fit_transform(iris_df.iloc[:, :-1])
svd_iris_df = pd.DataFrame(svd_iris_data, columns=['svd_component_1', 'svd_component_2'])
svd_iris_df['target'] = iris_data.target
fig, axs = plt.subplots(figsize=(16, 6), nrows=1, ncols=2, squeeze=False)
sns.scatterplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='target', ax=axs[0][0])
sns.scatterplot(data=svd_iris_df, x='svd_component_1', y='svd_component_2', hue='target', ax=axs[0][1])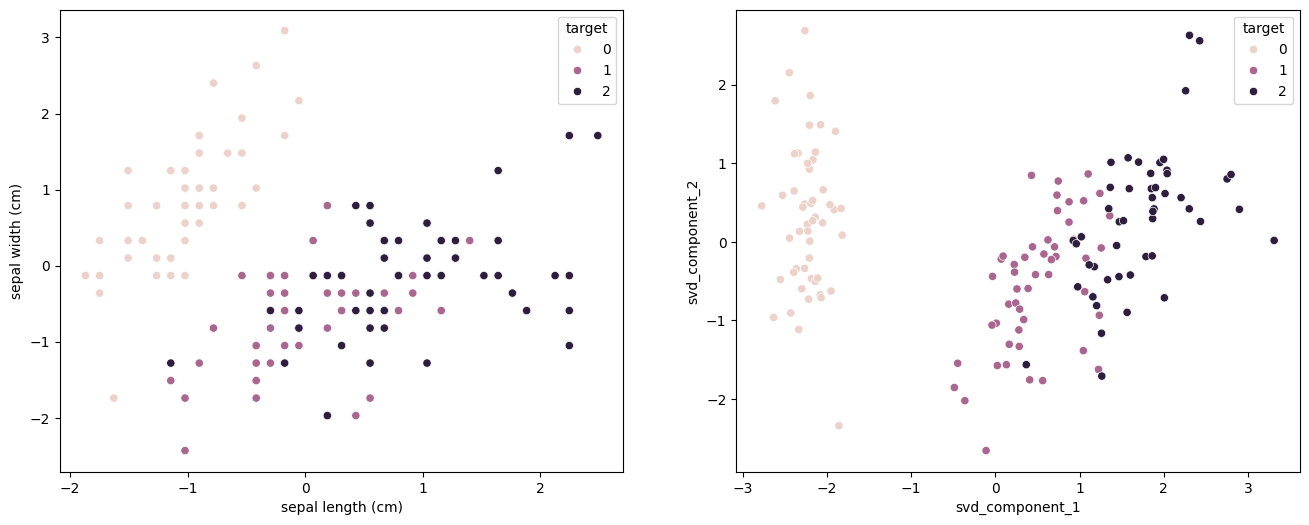
6. NMF
NMF(Non-negative Matrix Factorization)는 이름에서도 알 수 있듯이 음수 값을 가지지 않는 행렬을 분해하는 기법입니다.
행렬 X는 행렬 W와 H로 분해될 수 있으며 X의 크기가 m x n이라면 W와 H는 각각 m x p, p x n크기를 가지게 되며 각 행렬의 의미는 다음과 같습니다.
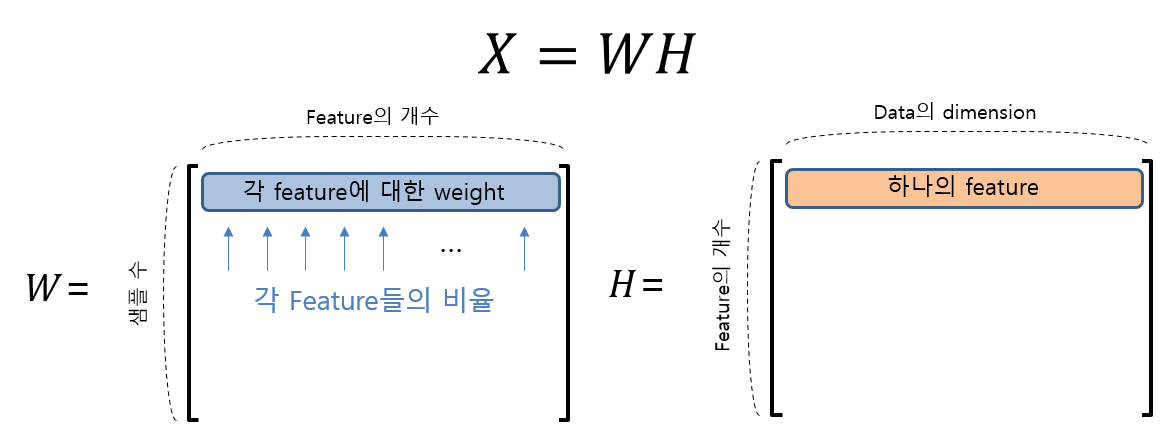
이미지 출처
다음은 sklearn의 NMF를 이용해 구현해본 것입니다.
from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
iris_data = load_iris()
iris_df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
iris_df['target'] = iris_data.target
nmf = NMF(n_components=2)
nmf_iris_data = nmf.fit_transform(iris_df.iloc[:, :-1])
nmf_iris_df = pd.DataFrame(nmf_iris_data, columns=['nmf_component_1', 'nmf_component_2'])
nmf_iris_df['target'] = iris_data.target
sns.scatterplot(data=nmf_iris_df, x='nmf_component_1', y='nmf_component_2', hue='target')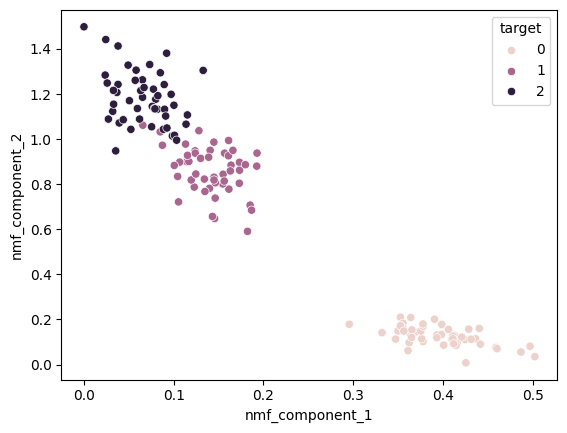
7. 정리
위에서 언급한 차원 축소 방법들(feature extraction)은 전처리를 하고 수행하는 것이 일반적입니다.
저같은 경우는 PCA, LDA에서 StandardScaler를 적용하지 않았지만 SVD, NMF에서는 사용한 걸 볼 수 있습니다.
정석대로면 PCA, LDA에서도 사용하는 것이 맞습니다.
