[ML] Clustering1 (군집화) K-Means / Mean Shift

조치연·2025년 4월 6일
MLMean shiftk-means
1

ML

목록 보기
13/17

오늘은 군집화에 대해 공부해봤습니다.
평소 관심을 가지지 않았던 분야이지만, 공부를 하면 할수록 군집화가 얼마나 중요한지 알게 되었습니다.

대회를 출전하면서 데이터를 빠르게 판단하는 능력부터 전체적인 EDA와 모델 성능 향상에 얼마나 중요한 역할을 하는지 알게되어 자세하게 공부했습니다.😊


📚 K-Means (K-평균)

K-평균은 군집화에서 가장 일반적으로 사용되는 알고리즘입니다.

K-평균은 군집 centroid(중심점)라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법입니다.


✅ 작동 원리

K-평균 알고리즘의 작동 원리는 다음과 같습니다.

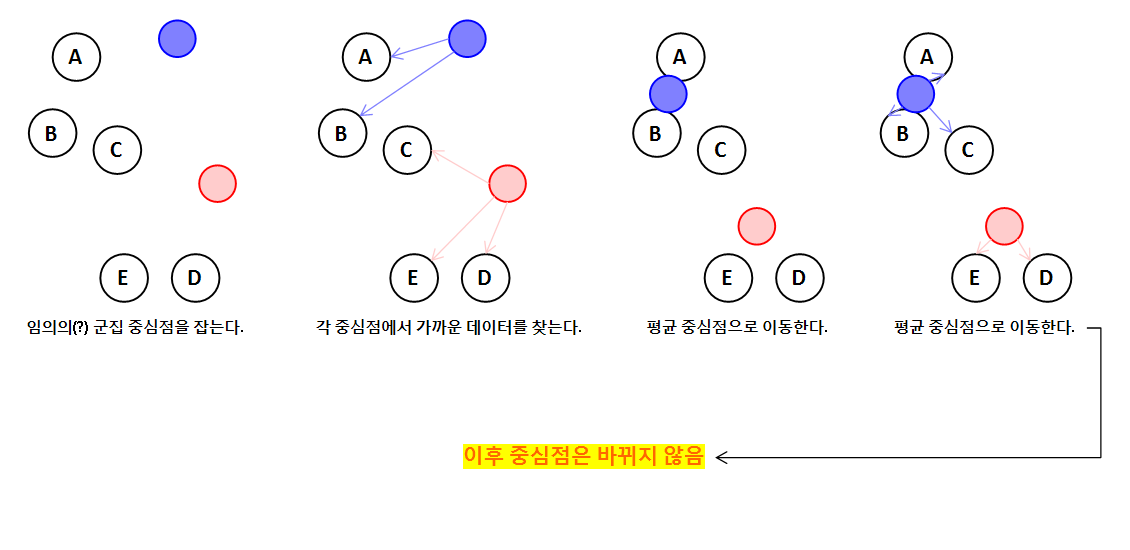
  • 특정 알고리즘을 이용해 임의의 지점을 군집 중심점으로 잡는다.
  • 각 군집 중심점에서 상대적으로 가까운 데이터들을 찾는다.
  • 각 중심점에 할당된 데이터의 평균으로 중심점을 이동한다.
  • 어떤 중심점도 새롭게 갱신되지 않을 때까지 반복한다.

이를 그림으로 표현하면 다음과 같습니다.
(목표로 하는 군집의 개수는 2개라고 가정했습니다.)

K-평균의 장단점은 다음과 같습니다.

장점

  • 일반적인 군집화에서 많이 활용됩니다.
  • 알고리즘이 쉽고 간결합니다.

단점

  • 거리 기반 알고리즘이기 때문에 피처 수가 매우 많을 경우 성능이 떨어집니다.
  • 수행 횟수가 많아지면 속도가 느려집니다.
  • 몇 개의 군집을 선택할지 가이드하기가 어렵습니다.


✅ KMeans Class

사이킷런 패키지는 KMeans 클래스를 제공합니다.
KMeans 클래스는 다음과 같은 하이퍼 파라미터를 가지고 있습니다.

class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init='auto', max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')

이중 주요 파라미터는 다음과 같습니다.

parameter

  • n_clusters: 군집화할 개수(군집 중심점의 개수)
  • init: 초기에 군집 중심점(centroid) 좌표를 찾는 알고리즘
  • max_iter: 최대 반복 횟수(이 회전 이전에 중심점 이동이 없으면 종료됩니다.)

이렇게 만들어진 KMeans 클래스의 주요 속성은 다음과 같습니다.

attribute

  • labels_: 각 데이터를 예측한 값(속해있는 중심점)
  • cluster_centers_: 각 군집 중심점 좌표

아래는 iris data를 기반으로 KMeans 클래스를 시각화 한 것입니다.

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

iris_data = load_iris()
iris_df = pd.DataFrame(data=iris_data.data, columns=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'])
iris_df['target'] = iris_data.target
iris_df
# cluster된 값을 데이터 프레임으로 만들기.

cluster_data = KMeans(n_clusters=3, init='k-means++', n_init='auto', max_iter=300).fit_predict(iris_df.iloc[:, :-1])
iris_df['cluster'] = cluster_data
# 시각화를 편하게 하기위해 PCA 변환 수행.

pca = PCA(n_components=2)
ftrs = pca.fit_transform(iris_df.iloc[:, :4])
iris_df['ftr1'] = ftrs[:, 0]
iris_df['ftr2'] = ftrs[:, 1]
markers = ['^', 'o', 's']

for i, marker in enumerate(markers):
    iris_gubuns = iris_df[iris_df['cluster']==i]
    plt.scatter(x=iris_gubuns['ftr1'], y=iris_gubuns['ftr2'], marker=markers[i], label=i)

plt.title('3 Clusters')
plt.xlabel('ftr1')
plt.ylabel('ftr2')
plt.legend()
plt.show()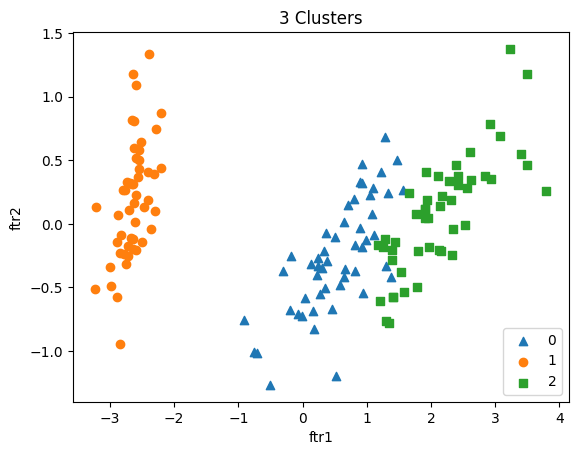


KMeans가 예측한 값은 실제 타겟 값과 다를 수 있음에 주의해야 합니다.
위 예제의 경우 실제 타겟 값과 모델이 클러스터 한 값이 어떻게 다른지 groupby를 통해 살펴보겠습니다.

iris_df.groupby('target')['cluster'].value_counts()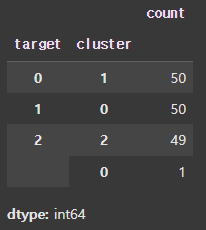


target 0은 cluster 1로, target 1은 cluster 0으로 target 2는 cluster 2로 매핑된 것을 볼 수 있습니다.

이번에 K-Means를 공부하면서 make_blobs API에 대해 공부했습니다.
make_blobs는 대표적인 군집화용 데이터 생성기 입니다.

이를 활용해서 K-Means를 시각화 해보겠습니다.

from sklearn.datasets import make_blobs

cluster_features, cluster_target = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0)
cluster_df = pd.DataFrame(data=cluster_features, columns=['ftr1', 'ftr2'])
cluster_df['target'] = cluster_target

markers = ['^', 'o', 's']
targets = np.unique(cluster_df['target'])

fig, (ax1, ax2) = plt.subplots(figsize=(16, 5), ncols=2)

for i, target in enumerate(targets):
    cluster_gubuns = cluster_df[cluster_df['target']==target]

    ax1.scatter(x=cluster_gubuns['ftr1'], y=cluster_gubuns['ftr2'], marker=markers[i], label=target)

ax1.set_title('target data')
ax1.set_xlabel('ftr1')
ax1.set_ylabel('ftr2')
ax1.legend()

kmeans = KMeans(n_clusters=3, max_iter=300)
kmeans.fit(cluster_df.iloc[:, :-1])
cluster_df['cluster'] = kmeans.labels_
center_x_ys = kmeans.cluster_centers_

clusters = np.unique(cluster_df['cluster'])

for i, cluster in enumerate(clusters):
    cluster_gubuns = cluster_df[cluster_df['cluster']==cluster]
    center_x, center_y = center_x_ys[i]
    ax2.scatter(x=cluster_gubuns['ftr1'], y=cluster_gubuns['ftr2'], marker=markers[i], label=cluster)

    ax2.scatter(x=center_x, y=center_y, marker=markers[i], s=200, c='w', edgecolors='k', alpha=0.9)
    ax2.scatter(x=center_x, y=center_y, marker='${0}$'.format(i), s=70, c='k', edgecolors='k')

ax2.set_title('cluster data')
ax2.set_xlabel('ftr1')
ax2.set_ylabel('ftr2')
ax2.legend()

plt.show()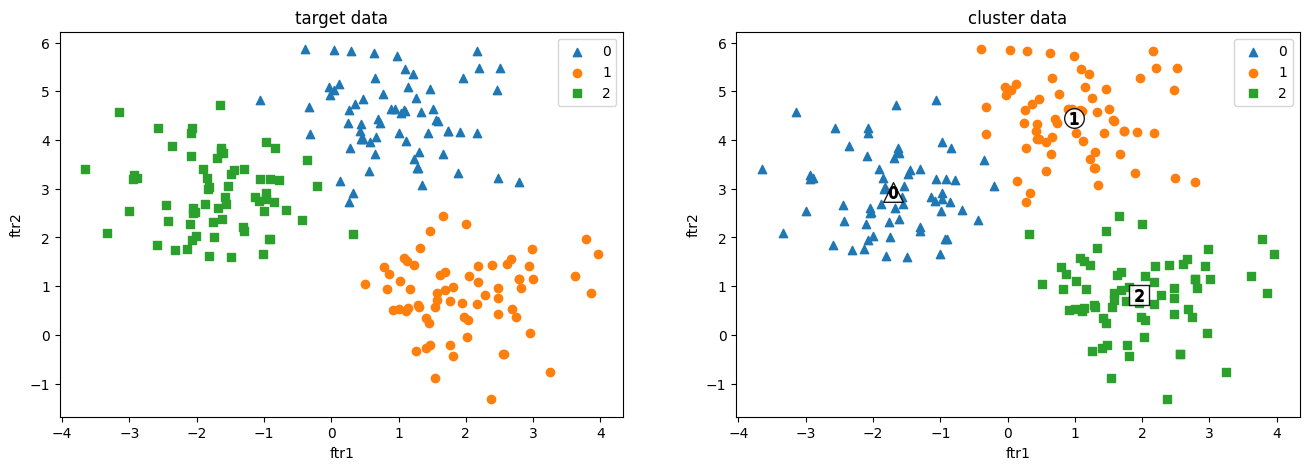


왼쪽은 make_blobs로 만든 원본 데이터 셋이며, 오른쪽은 그것을 클러스터링 한 것입니다.
앞에서 말씀 드렸듯이 클러스터링 값이 타겟 값과 다른 것은 당연한 것입니다.

모델이 대표적으로 예측 못한 부분은 다음과 같았습니다.



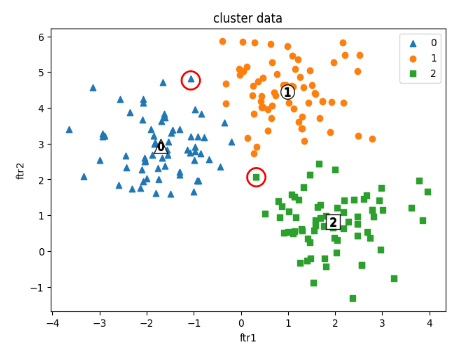
📚 Mean Shift (평균 이동)

평균 이동은 K-평균과 유사하게 중심을 군집의 중심으로 지속적으로 움직이면서 군집화를 수행합니다.

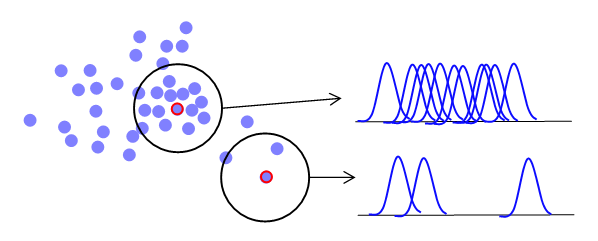
하지만, K-평균이 평균 거리를 기반으로 중심점이 이동하는 반면에 평균 이동은 데이터의 밀도가 높은 곳으로 중심점을 이동시킵니다.

평균 이동 군집화는 데이터가 모여있는 곳이 중심점이라는 생각에서 착안한 것입니다.
즉, 가장 데이터가 모여있어 확률 밀도 함수가 피크인 점을 군집 중심점으로 선정합니다.



✅ Kernel Density Estimation (커널밀도추정)

평균 이동 알고리즘의 작동원리를 이해하려면 커널밀도추정을 알아야 합니다.


✔️ Density Estimation (밀도추정)

우리는 하나의 변수에 대한 여러가지 데이터를 가지고 변수의 본질을 파악하고자 노력합니다.

즉, 우리는 변수에 대해 밀도를 추정하려고 합니다. 변수에 대한 밀도를 추정하면 변수에 대한 평균, 분산, 확률을 알 수 있기 때문입니다.

density(밀도)는 수학적으로 "질량/부피"로 나타나지만, 밀도추정, 기계학습, 확률, 통계 등에서는 probability density(확률 밀도)를 의미합니다.

다시말해서, 어떤 변수 x의 밀도를 추정한다는 것은 x의 확률밀도함수(pdf, probability density function)를 추정한다는 것입니다.



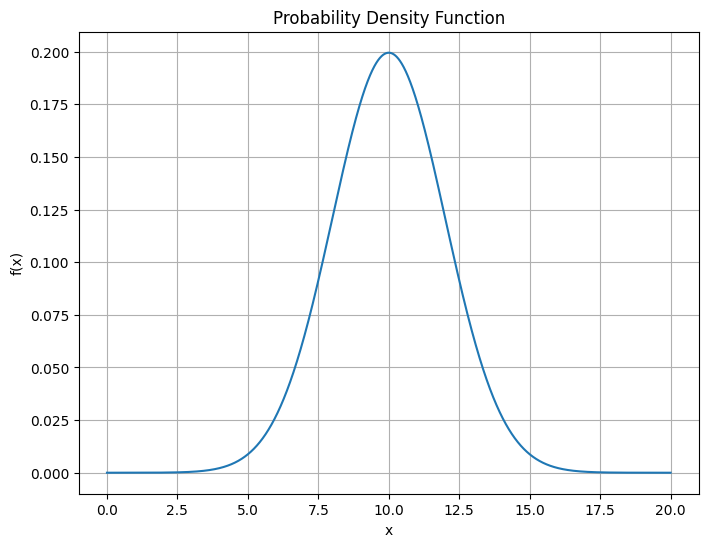
✔️ Parametric vs. Non-Parametric 밀도추정

이렇게 변수의 밀도추정을 하는 방식은 두 가지가 있다.(Parametric / Non-Parametric)

Parametric 밀도추정방식

Parametric 밀도추정방식은 미리 pdf를 정해놓고 입력 데이터만 입력하는 것입니다.
이런 경우 데이터로부터 평균과 분산만 구하면 됩니다.
하지만, 당연히 현실에서는 이런 경우가 거의 없습니다.

Non-Parametric 밀도추정방식

Non-Parametric 밀도추정방식은 사전 모델 없이 순수하게 데이터로만 확률밀도함수를 추정하는 것입니다.
Non-Parametric 밀도추정방식의 대표적인 예로 히스토그램이 있습니다.
데이터로부터 히스토그램을 만들면 이를 정규화하여 확률밀도함수를 만드는 것입니다.

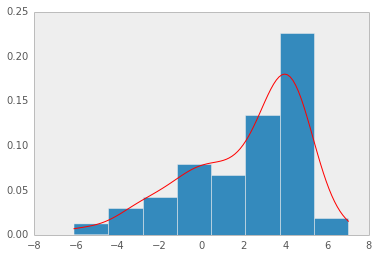
하지만, 이런 경우 확률밀도함수가 bin의 경계에서 불연속성이 나타나며, 고차원 데이터에서는 메모리 문제로 사용하기 힘들다는 단점이 있습니다.


✔️ 커널밀도추정(KDE, Kernel Density Estimation)

커널밀도추정도 Non-Parametric 방법 중 하나입니다.
이름에서 알 수 있듯이, kernel(커널)함수를 이용하여 확률밀도함수를 추정합니다.
(기존의 히스토그램 문제에 커널 함수를 적용.)

Kernel Function (커널 함수)

수학적으로 커널 함수란, 원점을 중심으로 좌우 대칭이면서 적분값이 1인 non-negative 함수로 정의됩니다.
예를 들어, Gaussian(가우시안) 함수가 있습니다.

커널 함수로는 아래처럼 다양한 함수가 있습니다.

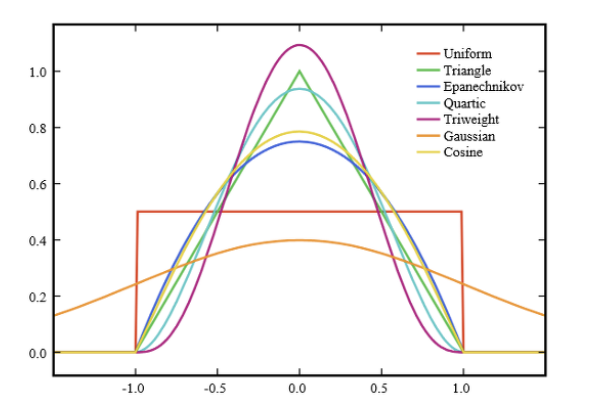
KDE에서는 각 데이터마다 중심으로 하는 커널 함수를 만듭니다.
이 커널 함수를 모두 더해서 데이터 개수로 나누어 정규화 시킵니다.
이렇게 확률밀도함수가 나오게 됩니다.

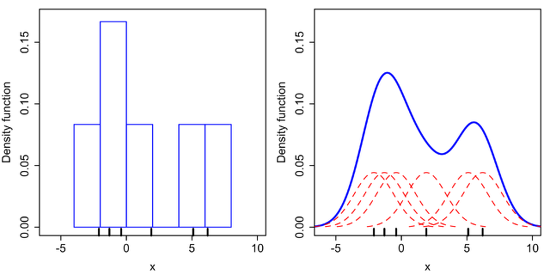
KDE를 통해 얻은 확률밀도함수는 히스토그램보다 더 부드럽습니다.
그리고 이런 부드러움은 커널 함수의 bandwidth(대역폭)에 따라 결정됩니다.
(대역폭이 클수록 부드러워짐)

이를 MeanShift 알고리즘에 대입해 생각해보면, 대역폭이 커질수록 모델이 군집화하는 수가 적어지며(underfitting), 작아질수록 모델이 군집화하는 수가 많아집니다.(overfitting)


✅ MeanShift Class / estimate_bandwidth Class

사이킷런 패키지는 MeanShift와 estimate_bandwidth 클래스를 제공합니다.
용도는 다음과 같습니다.

  • MeanShift: 평균 이동 알고리즘을 구현
  • estimate_bandwidth: 입력 데이터에서 최적의 bandwidth를 찾음

앞에서 말했듯이, 평균 이동 알고리즘에서 대역폭 값은 중요합니다.
대역폭이 클수록 군집의 개수가 적어지며, 작을수록 군집의 개수가 많아지기 때문입니다.
따라서 우리는 해당 데이터의 최적 대역폭을 찾아야 합니다.

사이킷런에서는 sklearn.cluster.estimate_bandwidth를 평균 이동 알고리즘을 위해 사용하라고 합니다.(대역폭이 주어지지 않은 경우)

from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift
from sklearn.cluster import estimate_bandwidth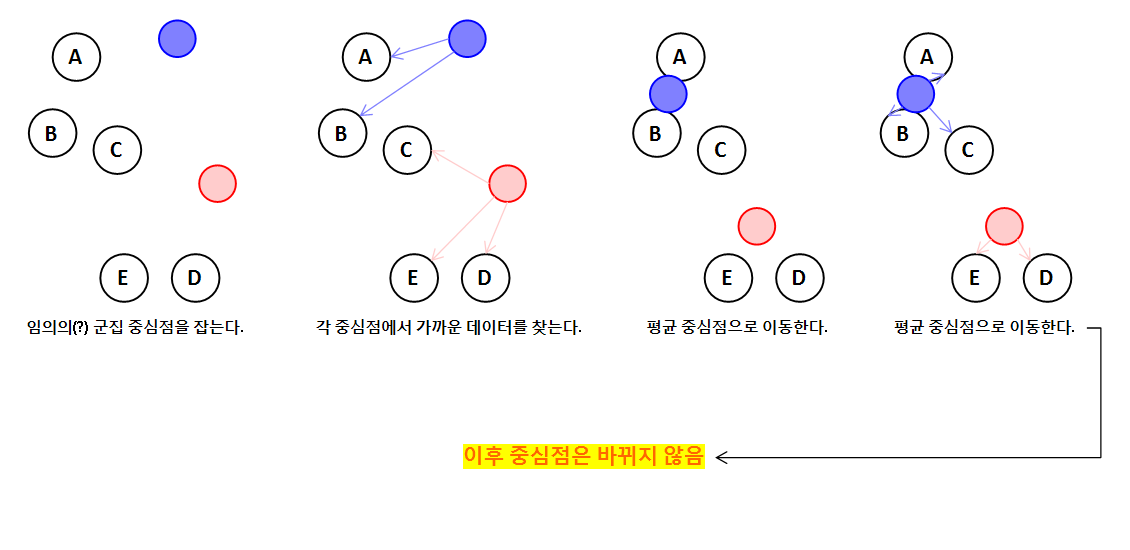![](https://velog.velcdn.com/images/chiyeon01/post/b0bfda4b-fb81-43f7-9dba-da809642b254/image.png)


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# make_blobs를 이용해 군집이 3개이고, feature는 2개인 데이터 셋을 만들고 시각화.
features, targets = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0)

cluster_df = pd.DataFrame(data=features, columns=['ftr1', 'ftr2'])
cluster_df['target'] = targets

markers = ['^', 'o', 's']

for i, marker in enumerate(markers):
    df = cluster_df[cluster_df['target']==i]

    plt.scatter(x=df['ftr1'], y=df['ftr2'], marker=marker, label=i)
    
plt.legend()
plt.show()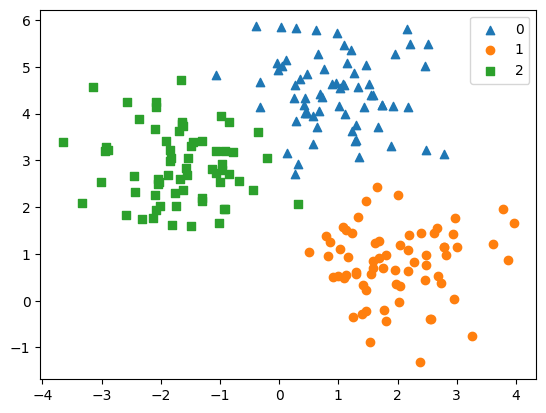

# estimate_bandwidth를 이용해 최적의 bandwidth를 찾기.
best_bandwidth = estimate_bandwidth(cluster_df.iloc[:, :-1])

# meanshift의 파라미터에 best_bandwidth 적용.
meanshift = MeanShift(bandwidth=best_bandwidth)
pred = meanshift.fit_predict(cluster_df.iloc[:, :-1])
print(best_bandwidth)

# 시각화.
cluster_df['cluster'] = pred

markers = ['^', 'o', 's']

for p in np.unique(pred):
    df = cluster_df[cluster_df['cluster']==p]

    plt.scatter(x=df['ftr1'], y=df['ftr2'], marker=markers[p], label=p)
    
plt.legend()
plt.show()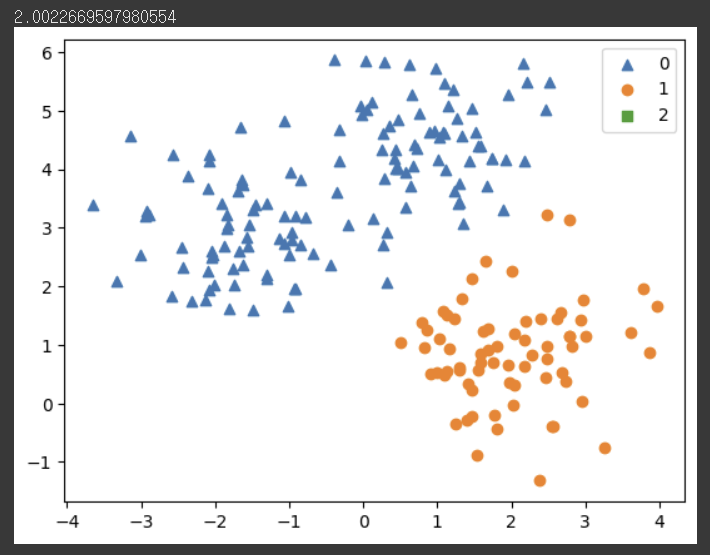


사이킷런 문서에서 제시한 가이드 라인을 따라 대역폭과 평균 이동을 따랐습니다.
하지만, 군집화가 잘 되지 않았음을 알 수 있습니다.

그렇다면 임의로 대역폭을 줄이면 어떻게 되는지 살펴보겠습니다.

# meanshift의 파라미터에 best_bandwidth 적용.
meanshift = MeanShift(bandwidth=1)

# 시각화.
cluster_df['cluster1'] = pred

markers = ['^', 'o', 's']

for p in np.unique(pred):
    df = cluster_df[cluster_df['cluster1']==p]

    plt.scatter(x=df['ftr1'], y=df['ftr2'], marker=markers[p], label=p)
    
plt.legend()
plt.show()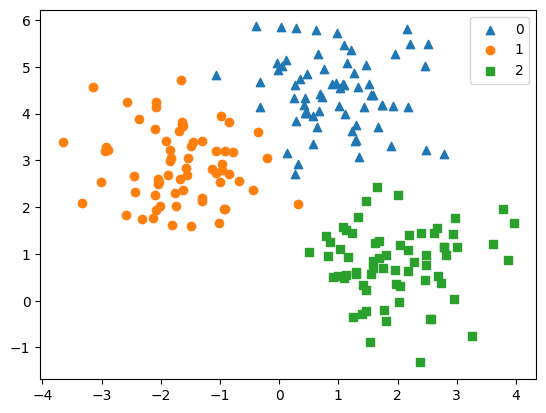


대역폭을 1로 조정했더니, 군집화가 상대적으로 잘 됐습니다.
이렇듯, 평균 이동 알고리즘은 대역폭에 영향을 많이 받는다는 단점이 있습니다.

평균 이동은 tracking과 같은 분야에서 좋은 성능을 보이니 참고하시면 되겠습니다.😊

이렇게 오늘은 K-Means 와 Mean Shift 알고리즘에 대해 공부했습니다.


📜 Reference

[개정판] 파이썬 머신러닝 완벽 가이드
Sklearn KMeans 공식문서
커널밀도함수에 대한 이해
Sklearn MeanShift 공식문서
Sklearn estimate_bandwidth 공식문서

profile
조치연
세종대학교 지능기전공학과 23
이전 포스트

[ML] 차원 축소(dimensionality reduction) PCA, LDA, SVD, NMF

다음 포스트

[ML] Clustering2 (군집화) GMM / DBSCAN

0개의 댓글