오늘은 가중치 초기화에 대해 공부하려고 합니다.
📚 Weight Initialization(가중치 초기화)
딥러닝에서 모델은 최적의 가중치 값을 찾으려고 합니다.
이때, 모델이 맨 처음으로 경사 하강법을 적용하려면 임의로 모델의 가중치를 설정해주어야 합니다.
이를 "가중치 초기화"라고 합니다.
그렇다면 가중치 초기화는 그냥 랜덤으로 하면 되는걸까요?
네, 됩니다.
하지만, 모델이 최적화하기 좋은 위치에서 시작하면 좋지 않을까요?
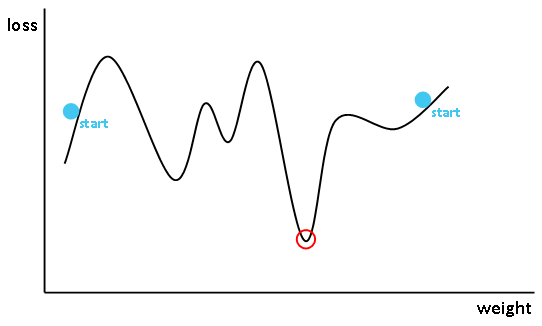
이번 장에서는 대표적인 Xavier Glorot, He 가중치 초기화에 대해 공부하려고 합니다.
✅ 좋은 가중치 초기화 조건
"좋은 가중치 초기화"기준이 존재할까요?
일반적으로 좋은 가중치 초기화 조건이라고 한다면 다음과 같습니다.
- 값이 동일하지 않아야 함.
- 충분히(적당히) 작아야 함.
- 분포도가 적당한 분산, 표준편차를 가져야 함.
분포라고 한다면 대표적으로 표준 정규 분포, 균등 분포가 있습니다.
정규 분포와 균등 분포를 이용한 가중치 초기화는 모두 각각의 이점이 있지만, 모두 하이퍼 파라미터에 영향을 크게 받습니다. 정규 분포의 경우 표준편차가 너무 작거나 크면, 그래디언트 소실과 폭주가 야기됩니다. 균등 분포도 마찬가지 입니다.
아래 그림처럼 평균이 0이며, 표준편차가 1과 0.2인 경우를 살펴보면 포준편차가 1인 경우가 상대적으로 가중치의 절댓값이 클 것입니다.
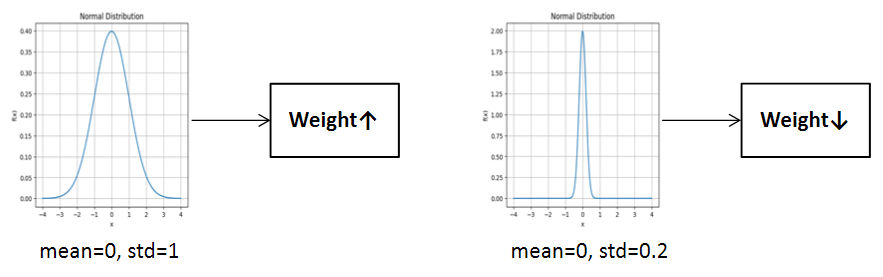
activation이 sigmoid인 경우,
이렇게 가중치의 분포가 크면 Output Feature Map은 1또는 0으로 수렴하기 쉬워집니다.
반대로 가중치의 분포가 작으면 Output Feature Map은 0.5로 수렴하기 쉬워집니다.
다시말해, 각각 미분값 손실과 Output이 0으로 수렴하는 현상이 생기게 됩니다.
✅ Xavier Glorot Initialization
Xavier 가중치 초기화 방법은 fan in과 fan out을 모두 고려합니다.(Glorot이라고도 부릅니다.)
즉, 입력 노드와 출력 노드의 개수를 감안하여 동적으로 가중치를 초기화 합니다.
Xavier 가중치 초기화는 표준 정규 분포와 균등 분포를 만들 수 있는데, 각각 한도값과 표준편차를 구하는 공식은 다음과 같습니다.

Xavier 가중치 초기화 방법은 일반적으로 활성화 함수가 tanh일 때, 효과가 더 좋다고 합니다.
✅ He Initialization
He 가중치 초기화 방법은 활성화 함수가 ReLU에 보다 최적화 된 방법입니다.
He 가중치 초기화 방법도 Xavier 가중치 초기화 방법과 마찬가지로 입력 노드와 출력 노드의 개수를 감안하여 동적으로 가중치를 초기화 합니다.
정규 분포와 균등 분포를 만드는 방식은 Xavier 가중치 초기화와 다른 점은 없습니다.
다만, 한도값과 표준편차 공식에서 fan out이 빠졌다는 특징이 있습니다.

기본적으로 텐서플로우에서는 Xavier 가중치 초기화를 디폴트로 정해놓습니다.
다음은 텐서플로우를 이용해 Layer에 가중치 초기화를 적용하는 코드입니다.
from tensorflow.keras.layers import Conv2D
# Xavier Initializer 적용.
# 균등분포
Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu', kernel_initializer='glorot_uniform')
# 정규분포
Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu', kernel_initializer='glorot_normal')
# He Initializer 적용.
# 균등분포
Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu', kernel_initializer='he_uniform')
# 정규분포
Conv2D(filters=32, kernel_size=(3, 3), padding='same', activation='relu', kernel_initializer='he_normal')