이번 장에서는 다항회귀를 이용해 Overfitting(과적합)에 대해 공부해보고,
이를 해결하기 위한 방법으로 Regularization(규제)에 대해 공부하려고 합니다.😊
또한, 편향과 분산에 대한 트레이드오프에 대해 편향과 분산의 정의를 확고히 하고자 합니다.
📚 Overfitting(과적합)
과적합이란, 모델이 학습 데이터에 너무 치우쳐 있어 실제 데이터 세트에서는 성능을 발휘하지 못하는 상태를 의미합니다.
Underfitting(과소적합)은 과적합의 반대 의미입니다.
실제 머신러닝 문제는 과적합에서 대부분 발생합니다.
예를들어, 아래의 코드와 결과를 살펴봅시다.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
X30 = np.sort(np.random.rand(30)) # Feature값 만들기.
X100 = np.sort(np.random.rand(100)) # true function의 입력 값.
y = np.cos(1.5*np.pi*X30) + 0.2 * np.random.randn(30) # target 값(약간의 잡음을 곁들인)
def true_function(X30):
return np.cos(1.5*np.pi*X30)
fig, axs = plt.subplots(figsize=(16, 6), nrows=1, ncols=3)
n_degree = [1, 4, 30]
for i, degree in enumerate(n_degree):
poly_X = PolynomialFeatures(degree=degree).fit_transform(X30.reshape(-1, 1))
model = LinearRegression()
model.fit(poly_X, y)
pred = model.predict(poly_X)
axs[i].scatter(X30, y, c='b')
axs[i].plot(X100, true_function(X100), c='g', label='true_function')
axs[i].plot(X30, pred, c='r', label='degree:{0} model'.format(degree))
axs[i].set_title('degree:{0}'.format(degree))
axs[i].legend()
plt.show()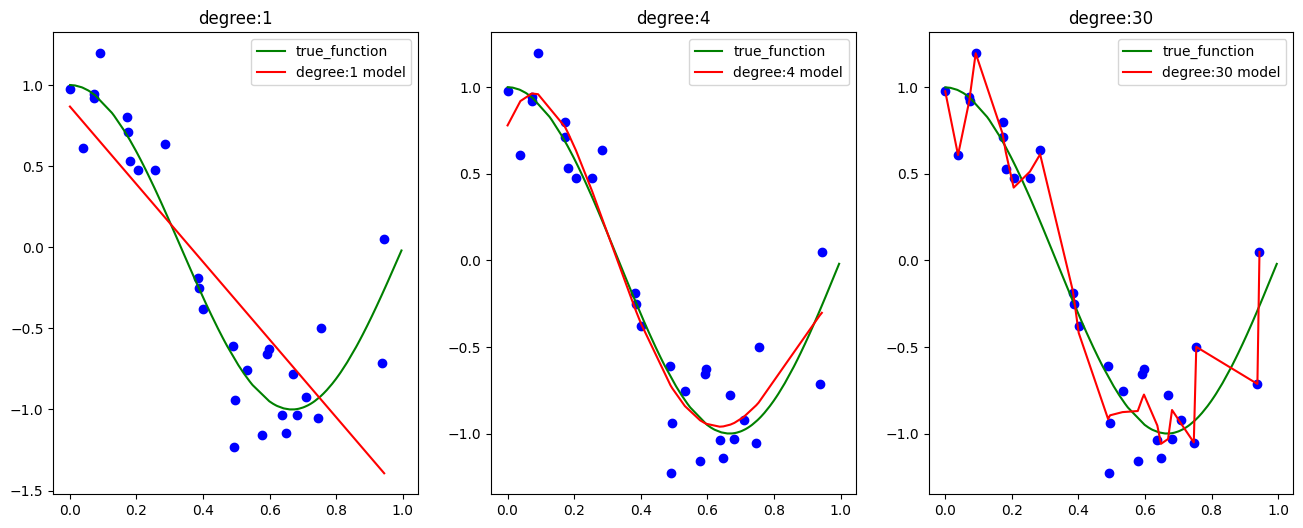
0-1까지 분포되어 있는 X feature에 대한 true function이 COSINE(1.5 * pi * X)일 때, degree값에 따라 모델이 어떻게 예측하는지 보겠습니다.
- degree=1: 모델이 1차 함수(직선)로 예측함을 볼 수 있습니다.
- degree=4: 모델이 어느정도 true function과 차이 없이 잘 예측했습니다.
- degree=30: 모델이 train data에 대해 과적합 되어있습니다.
degree=1인 경우는 과소적합, degree=30인 경우는 과적합이라고 볼 수 있겠습니다.
회귀 모델이 과적합 되는 경우 회귀계수가 기하급수적으로 커질 수 있습니다.
이는 조금이라도 학습 데이터와 다른 데이터가 들어온다면 오류값이 커질 수 있다는 의미입니다.
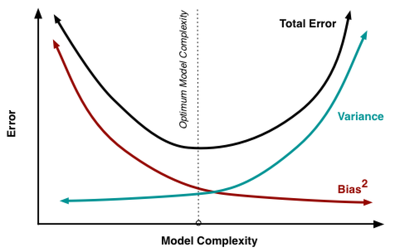
✅ Bias-Variance Trade off(편향-분산 트레이드오프)
과적합은 흔히 편향과 분산으로 설명할 수 있습니다.
과녁으로 설명하자면, 편향은 방향이고 분산은 그 방향에 대해서 얼마나 넓게 펴져있는지를 의미합니다.
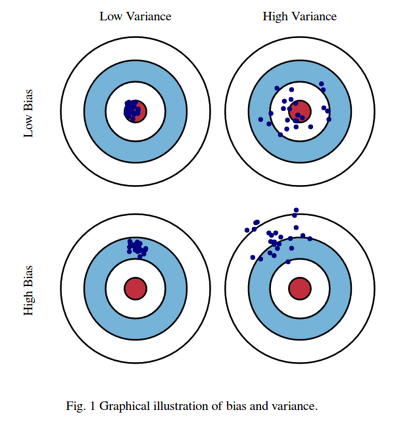
즉, 우리는 낮은 편향과 높은 분산을 목표로 합니다.
저는 이 그림에서 한 가지 의문이 생겼습니다.
분산은 알겠는데, 낮은 편향? 높은 편향?
여기서 말하는 편향은 측정 과정 혹은 모집단에서 표본을 추출하는 과정에서 발생하는 계통적인 오차 입니다. 말 그대로 오류값을 의미합니다. 그러니 편향이 낮은 것이 좋습니다.
이를 다시 해석하면 다음과 같습니다.
분산이 크고 편향이 낮으면 과적합, 분산이 작고 편향이 높으면 과소적합 입니다.
방향성이 일정하면 분산이 낮고, 편향은 커지기 쉽습니다.
방향성이 들쭉날쭉하면 분산이 높고, 편향은 작아지기 쉽습니다.
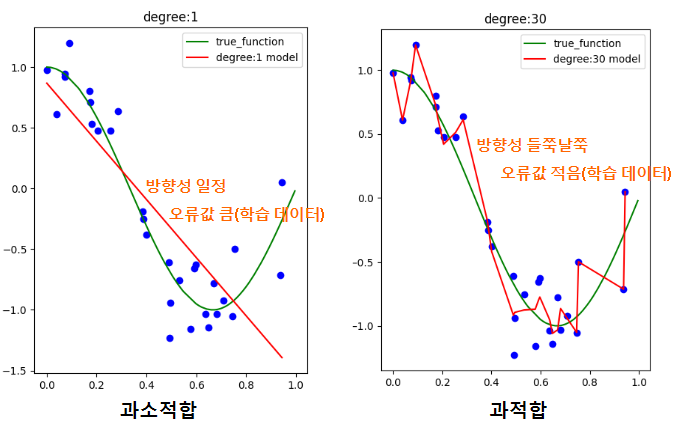
이렇게 편향과 분산의 개념을 이해하고 아래의 그림을 보면 이해하기 쉬울 것입니다.
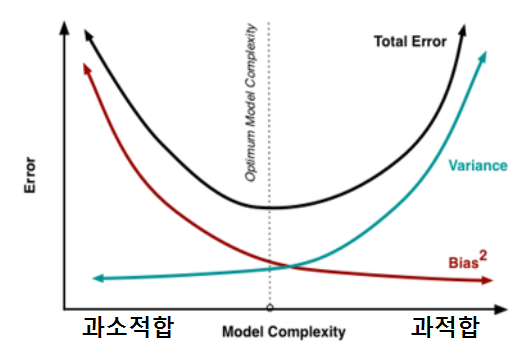
📚 Regularization(규제)
이렇게 과적합과 과소적합에 대해 배웠습니다.
다시한번 말하지만, 머신러닝에서 주요 문제는 과적합입니다.
우리는 이 문제를 해결하기 위해 규제라는 방법을 도입하게 됩니다.
기존의 선형회귀 모델의 비용함수는 RSS를 최소화하는, 즉 실제 값과 예측 값의 차이를 최소화 하는 것만 고려했습니다.
이렇게하면 편향은 낮아지지만, 분산이 높아집니다.
분산이 높아지는 주 원인은 피처 수가 많아지면서 회귀계수가 쉽게 커지기 때문입니다. 이럴 경우 변동성이 오히려 심해져서 테스트 데이터에서는 예측 성능이 저하되기 쉽습니다.
이를 해결하기 위해 비용함수는 RSS값만 낮추는 것이 아닌 회귀계수도 최소화 하는 방향으로 만듭니다.

첫 번째 식은 L2규제를 적용한 식이고, 두 번째 식은 L1규제를 적용한 식 입니다.
alpha값에 따라 규제를 얼마나 적용할 것인지 정할 수 있습니다.
alpha값이 커지면 규제도 커진다는 의미입니다.
L2 규제와 L1 규제 모두 RSS값과 회귀계수 모두를 줄이기 위한 것이지만, 다음과 같은 차이가 있습니다.
- L2 규제: 회귀계수 값을 작게 만드는 것을 목표로 합니다.
- L1 규제: 회귀계수중 필요없는 값을 0에 근접하게 만드는 것을 목표로 합니다.
✅ Ridge(릿지)
릿지 회귀는 선형회귀에 L2규제를 적용한 모델입니다.
릿지 회귀는 alpha값이 커질수록 회귀계수를 작게 만듭니다.
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
import numpy as np
import pandas as pd
housing = fetch_california_housing()
features = housing.data
targets = housing.target
house_df = pd.DataFrame(features, columns=housing.feature_names)
house_df['target'] = targets
coef_df = pd.DataFrame()
alphas = [0.1, 1, 10, 100]
for alpha in alphas:
model = Ridge(alpha=alpha)
scores = cross_val_score(model, features, targets, scoring='neg_mean_squared_error')
rmse = np.mean(np.sqrt(-1 * scores))
model.fit(features, targets)
coef_df['alpha:{0}'.format(alpha)] = model.coef_
print('##### alpha:{0} #####'.format(alpha))
print(round(rmse, 4))
coef_df.index = house_df.columns.tolist()[:-1]
coef_df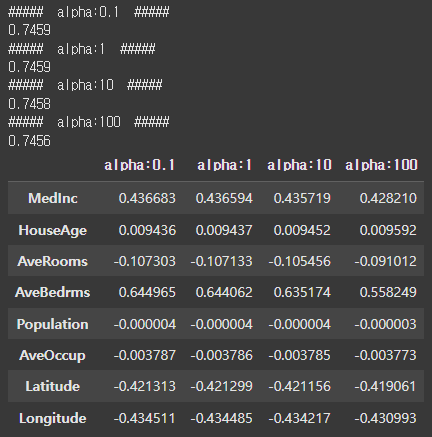
결과 값처럼 릿지 회귀의 alpha값이 커질수록 회귀계수는 상대적으로 작아짐을 알 수 있습니다.
(아쉽게도 boston 데이터가 윤리적 문제로 다운받아지지 않습니다.)
✅ Lasso(라쏘)
라쏘 회귀는 선형회귀에 L1규제를 적용한 모델입니다.
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Lasso
from sklearn.model_selection import cross_val_score
import numpy as np
import pandas as pd
housing = fetch_california_housing()
features = housing.data
targets = housing.target
house_df = pd.DataFrame(features, columns=housing.feature_names)
house_df['target'] = targets
coef_df = pd.DataFrame()
alphas = [0.01, 0.1, 1, 10]
for alpha in alphas:
model = Lasso(alpha=alpha)
scores = cross_val_score(model, features, targets, scoring='neg_mean_squared_error')
rmse = np.mean(np.sqrt(-1 * scores))
model.fit(features, targets)
coef_df['alpha:{0}'.format(alpha)] = model.coef_
print('##### alpha:{0} #####'.format(alpha))
print(round(rmse, 4))
coef_df.index = house_df.columns.tolist()[:-1]
coef_df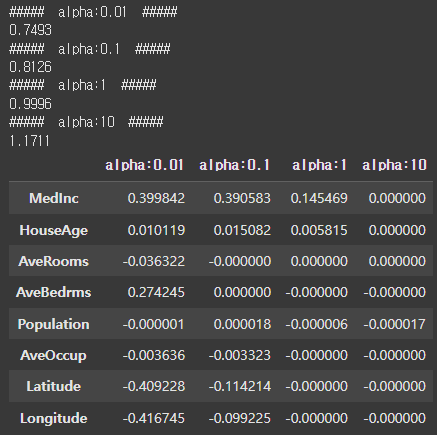
라쏘 회귀는 L1규제를 적용했기 때문에 alpha가 커질수록 특정 회귀값이 0에 가까워지는 것을 알 수 있습니다. 라쏘 회귀는 이러한 이유 때문에 Feature Selection에도 사용할 수 있습니다.
✅ Elastic Net(엘라스틱넷)
엘라스틱넷은 L2규제와 L1규제를 결합한 회귀 입니다.
따라서 엘라스틱넷 회귀 비용함수는 다음과 같습니다.
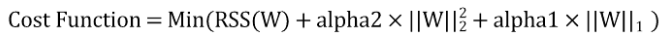
기존에 라쏘 회귀는 특정 회귀계수 값을 0으로 만드려는 성향이 강하기 때문에 회귀계수의 값이 급격하게 변동할 수 있습니다.
엘라스틱넷은 이런 성향을 완화하기 위해 L2규제를 라쏘 회귀에 추가한 것입니다.
sklearn에서 엘라스틱넷 회귀를 사용할 때, 주의할 점이 있습니다.
기존에 릿지와 라쏘 회귀의 파라미터와는 다르게 alpha1, alpha2가 아닌 alpha, l1_ratio 파라미터가 존재합니다.
alpha는 alpha1 + alpha2를 의미하며, l1_ratio는 그 중 alpha1의 비율을 의미합니다.
- alpha: alpha1 + alpha2
- l1_ratio: alpha1 / (alpha1 + alpha2)
코드를 살펴보면 다음과 같습니다.
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import cross_val_score
import numpy as np
import pandas as pd
housing = fetch_california_housing()
features = housing.data
targets = housing.target
house_df = pd.DataFrame(features, columns=housing.feature_names)
house_df['target'] = targets
coef_df = pd.DataFrame()
alphas = [0.01, 0.1, 1, 10]
for alpha in alphas:
model = ElasticNet(alpha=alpha, l1_ratio=0.5)
scores = cross_val_score(model, features, targets, scoring='neg_mean_squared_error')
rmse = np.mean(np.sqrt(-1 * scores))
model.fit(features, targets)
coef_df['alpha:{0}'.format(alpha)] = model.coef_
print('##### alpha:{0} #####'.format(alpha))
print(round(rmse, 4))
coef_df.index = house_df.columns.tolist()[:-1]
coef_df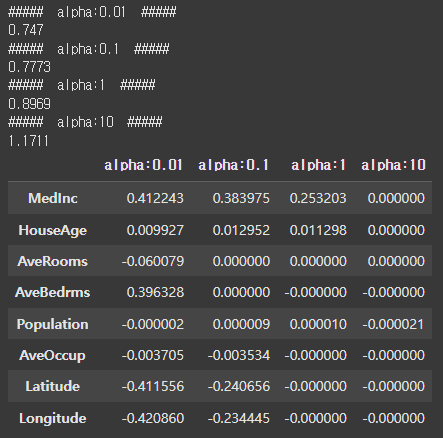
⭐ 수학적 기교(왜 L2와 L1은 다른 결과를 가지는가?)
이렇게 오늘은 Overfitting/Underfitting에 대해 복습하는 시간을 가지며, 이를 통해 생기는 문제와 이를 해결하는 Regularization에 대해 공부했습니다.
개인적으로 가장 궁금했던 부분은 "어째서 L1규제는 회귀계수를 0으로 만드려는 경향이 강하고, L2규제는 작게 만드려는 경향이 강한가?" 였습니다.
이는 우리가 회귀에 경사하강법이 사용된다는 것을 알면 충분히 이해 가능한 부분이었습니다.
자세한 수학적 공식은 사용하지 않겠습니다.
L2규제의 비용함수를 보면 W에 제곱을 했습니다.
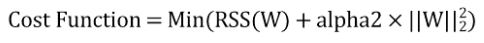
경사하강법을 이용하면 각 비용함수에 편미분을 적용합니다.
2차함수를 미분하면 1차함수가 됩니다.(물론 위의 비용함수는 2차함수가 아닙니다!)
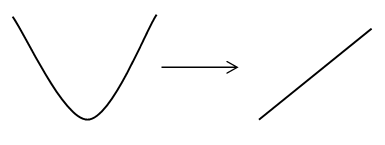
이는 L1규제보다 더 부드러운 변화를 이끌어 냅니다.
이미 작은 회귀계수에는 상대적으로 더 작은 변화가 일어나며, 큰 회귀계수에는 상대적으로 더 큰 변화가 일어납니다.
L1규제의 비용함수는 W의 절댓값을 더한 것에 불과합니다.
이는 1차함수를 의미하며, 미분을 통해 상수 값을 얻게 됩니다.
즉, 기존 회귀계수의 크기에는 상관없이 같은 변화가 일어난다는 것을 의미합니다.
여기에 쓰인 수학적 기법을 더 자세히 공부하고 싶다면 마지막 참고에 《왜 L2와 L1은 다른 결과를 가지는가?》링크를 참고해 주시기 바랍니다.
📜 Reference
[개정판] 파이썬 머신러닝 완벽 가이드
Underfitting vs. Overfitting
머신러닝 모델에서 편향과 분산의 개념 이해
왜 L2와 L1은 다른 결과를 가지는가?